Кр 1. Исследование режимов работы симметричного и несимметричного потребителей электрической энергии в трехфазных электрических цепях
 Скачать 2.21 Mb.
|
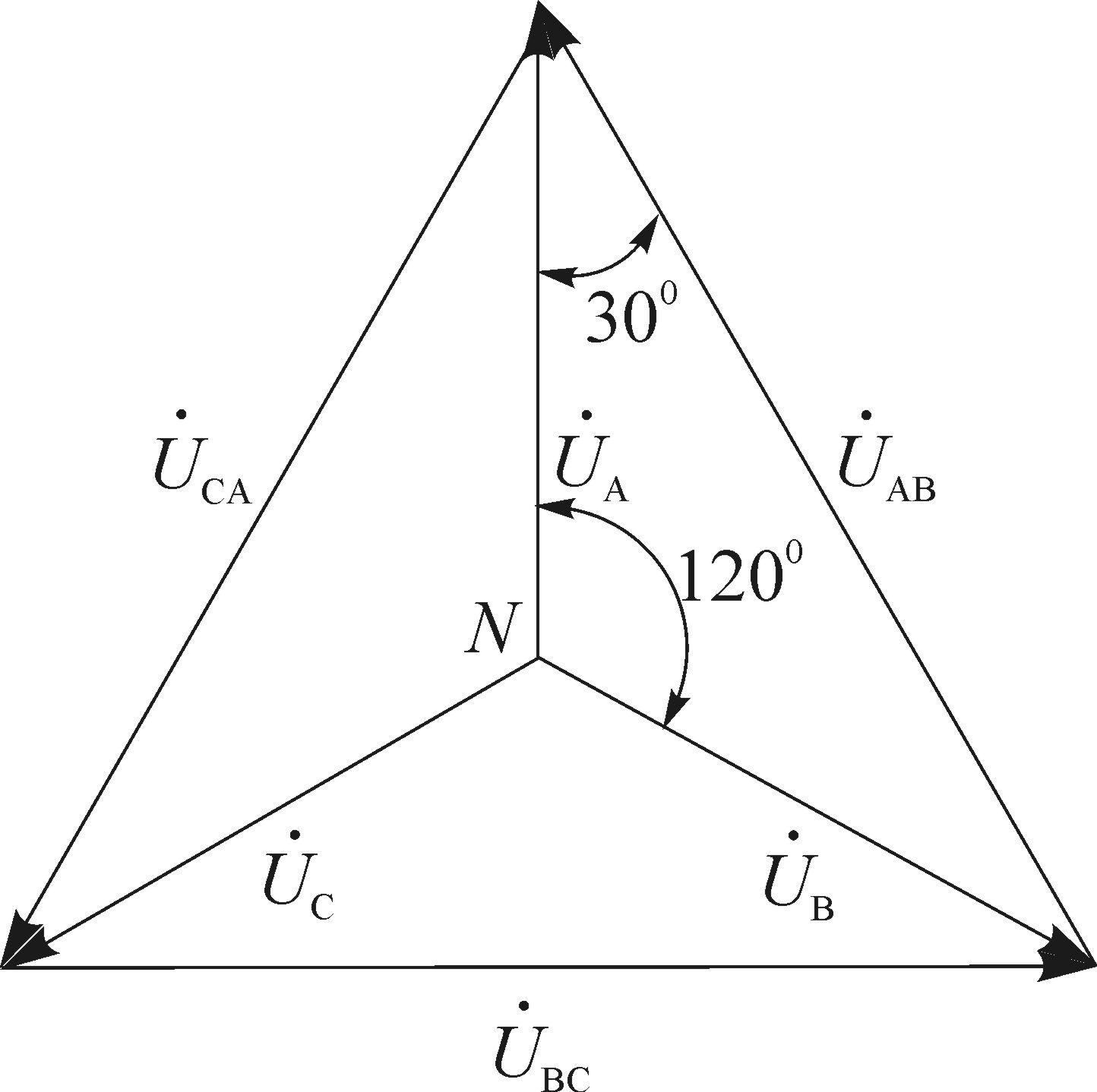
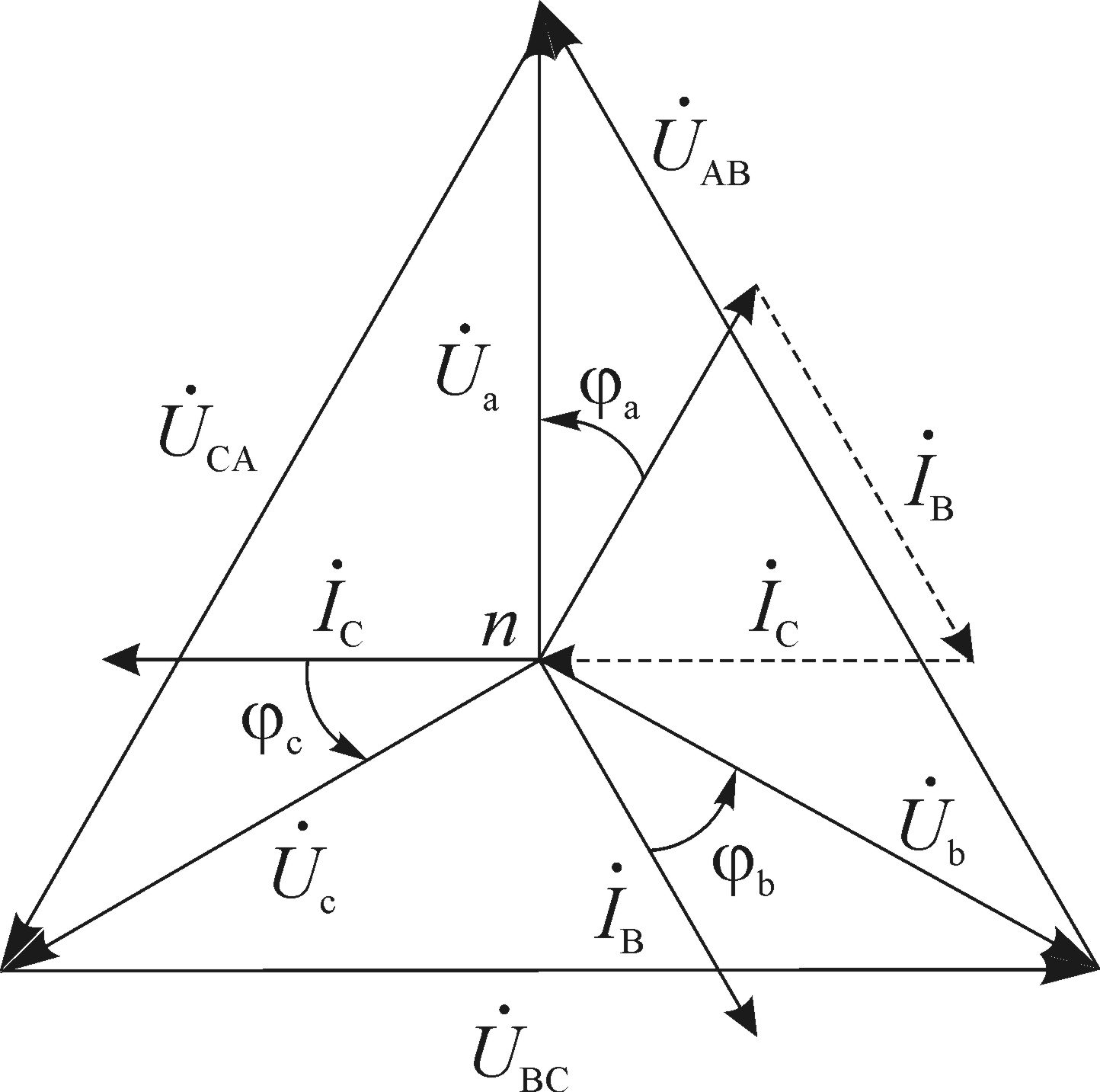
3. Трехфазные электрические цепиЦель работы: исследование режимов работы симметричного и несимметричного потребителей электрической энергии в трехфазных электрических цепях; определение основных соотношений между фазными и линейными токами и напряжениями при симметричной нагрузке и включении потребителей звездой и треугольником. Основные теоретические положенияСимметричная трехфазная ЭДС Трехфазные цепи представляют собой частный случай многофазных цепей переменного тока. Многофазными цепями называется совокупность однофазных электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, отличающиеся по фазе одна от другой. Каждую из цепей, входящих в многофазную цепь, называют фазой. Наибольшее распространение в современной электроэнергетике получили трехфазные цепи. К преимуществам использования трехфазных электрических цепей по сравнению с однофазными следует отнести: возможность получения вращающегося магнитного поля и использования наиболее простых, надежных и дешевых асинхронных электродвигателей, меньший расход проводниковых материалов на сооружение линий электропередачи, высокие экономические показатели трехфазных генераторов и трансформаторов, возможность подключения к трехфазной сети приемников, рассчитанных на два различных по значению напряжения. Благодаря этим преимуществам трехфазные цепи получили исключительно широкое применение. Трехфазная цепь состоит из трех основных элементов: источника, линии передач, приемников (потребителей). В качестве трехфазных источников напряжений на электрических станциях используются трехфазные синхронные генераторы, на статоре которых размещается трехфазная обмотка, фазы которой смещены в пространстве относительно друг друга на угол 120. Трехфазный генератор схематически изображен на рис. 3.1. Каждая фаза обмотки генератора условно показана одним витком. Начала фаз обозначаются буквами А, В, С, а соответствующие им концы X, Y, Z. При вращении ротора, выполненного в виде электромагнита постоянного тока, в неподвижных обмотках статора будут индуцироваться переменные ЭДС, сдвинутые друг относительно друга по фазе также на 120 (2/3): eА = EАm sin t; eB = EBmsin (t 2/3); eC = ECm sin (t + 2/3), где EAm, EBm и EСm –– амплитудные значения ЭДС соответственно фаз А, В и С. Положительное направление ЭДС в каждой фазе от конца обмотки к началу обмотки.  Рис. 3.1. Трехфазный синхронный генератор и фазы обмотки его статора ЭДС обмоток имеют одинаковые амплитуды и сдвинуты по фазе относительно друг друга на угол 2/3. Такая система называется симметричной. На рис. 3.2 показаны векторные диаграммы трехфазной симметричной системы ЭДС. Система ЭДС, в которой  отстает от  , а  отстает от  , называется системой прямой последовательности фаз (рис. 3.2, а). Если изменить направление вращения ротора генератора, то последовательность фаз ЭДС изменится и будет называться обратной (рис. 3.2, б).Схема соединения "звезда" Обмотки современных трехфазных генераторов соединяются, как правило, по схеме "звезда". Звездой называется такое соединение фаз генератора или трехфазной нагрузки, при котором одноименные зажимы (например, концы фаз X, Y, Z) объединяются в одну общую точку (рис. 3.3). Приемники электрической энергии соединяются по схемам "звезда" и "треугольник". Общие точки обмоток генератора (точка N) и ветвей звезды приемника (точка n) называются нейтральными или нулевыми точками, соединяющий их провод — нейтральным или нулевым проводом. Провода, соединяющие начала фаз генератора и приемника, называют линейными. Цепь, изображенная на рис. 3.3, называется четырехпроводной. Отключая нулевой провод, получим трехпроводную трехфазную цепь, соединенную звездой. Напряжение между началом и концом каждой фазы генератора (нагрузки) называют фазным: 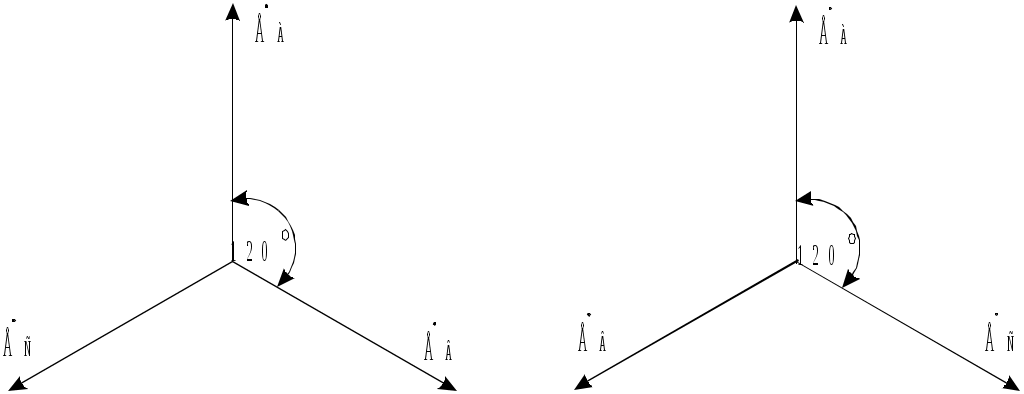 –– фазные напряжения генератора, –– фазные напряжения нагрузки. б) Рис. 3.2. Векторная диаграмма трехфазной симметричной системы ЭДС синхронного генератора: а - прямая последовательность чередования фаз; б - обратная последовательность чередования фаз 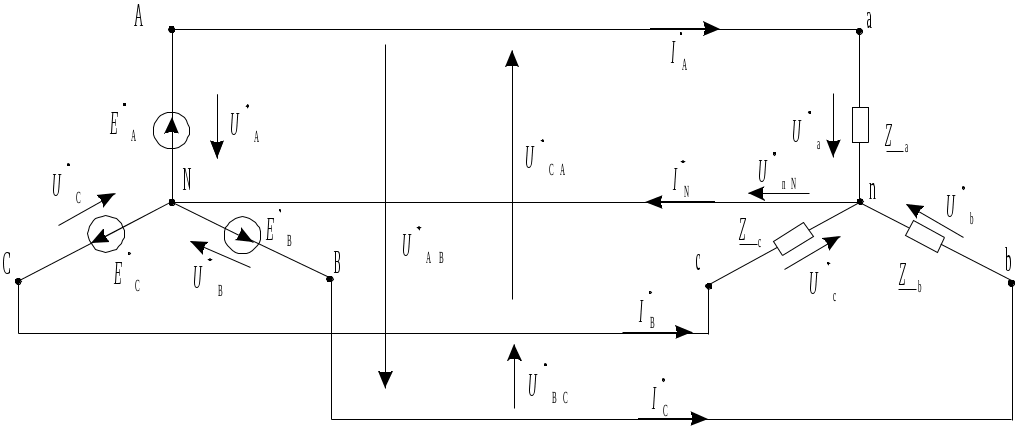 Рис. 3.3. Схема четырехпроводной трехфазной цепи Напряжения между началами фаз генератора (нагрузки) называют линейными –  .На практике часто пренебрегают внутренним сопротивлением фаз генератора, поэтому фазные напряжения генератора считают равными фазным ЭДС и изображают их симметричной системой векторов (рис. 3.4).Линейные и фазные напряжения генератора связаны следующими соотношениями, полученными по второму закону Кирхгофа:  В соответствии с этими уравнениями построена топографическая векторная диаграмма линейных напряжений (рис. 3.4). Для генератора величина каждого линейного напряжения будет в  раз больше величины фазного напряжения: По аналогии с фазными и линейными напряжениями различают фазные и линейные токи.  Токи IA, IB и IC в соответствующих линейных проводах называются линейными, токи, протекающие по фазам, — фазными, а ток IN в нейтральном проводе называется нейтральным.Из схемы рис. 3.3 видно, что обмотка генератора, линейный провод и приемник, принадлежащие одной фазе, соединяются последовательно, следовательно, фазные токи равны соответствующим линейным:  .Ток в нейтральном проводе может быть определен по первому закону Кирхгофа, на основании которого для нейтральной точки потребителя можно записать уравнение  .Следовательно, ток в нейтральном проводе равен векторной сумме фазных токов. Применяя второй закон Кирхгофа к контурам anba, bncb и cnac (см. рис. 3.3) можно получить следующие соотношения между линейными и фазными напряжениями потребителя:  Эти соотношения справедливы независимо от величины и характера сопротивлений фаз потребителя, а также от того, имеется или отсутствует нейтральный провод. Нагрузка, при которой комплексные сопротивления всех фаз потребителя равны между собой:  , называется симметричной. При этом равны в отдельности активные и реактивные сопротивления всех фаз: Ra = Rb = Rc и Xa = Xb = Xc.Сопротивления линейных проводов, так же как и сопротивление нейтрального, обычно малы, и их можно не учитывать. В этом случае комплексные значения линейных и фазных напряжений приемника оказываются равными соответственно комплексным значениям линейных и фазных напряжений генератора. Следовательно, векторная диаграмма напряжений потребителя будет совпадать с векторной диаграммой напряжений генератора (рис. 3.4). Из векторной диаграммы следует, что при соединении потребителя электроэнергии звездой при симметричной нагрузке между фазными и линейными напряжениями потребителя существует соотношение:  .Ток в каждой фазе может быть определен по закону Ома для цепи синусоидального тока:  и  . (3.1)Так как фазные напряжения и фазные сопротивления потребителя электроэнергии равны между собой, то фазные токи при симметричной нагрузке также равны по значению IА = IB = IC = IФ и углы сдвига векторов фазных токов относительно векторов фазных напряжений одинаковы a = b = c = и определяются из выражений: a = arctg(Xa/Ra) = b = arctg(Xb/Rb) = c = arctg(Xc/Rc). При симметричной нагрузке фазные токи образуют симметричную систему, вследствие чего ток в нейтральном проводе равен нулю:  ,поэтому при симметричной нагрузке этот провод становится не нужным и применять его нет смысла. Векторная диаграмма напряжений и токов при симметричной активно-индуктивной нагрузке дана на рис. 3.5.
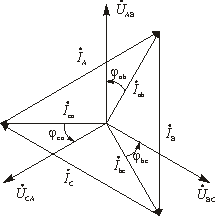
При несимметричной нагрузке комплексные сопротивления всех трех фаз в общем случае не равны между собой, т.е.  .Пренебрегая сопротивлениями линейных проводов, можно считать, что линейные напряжения потребителя независимо от характера нагрузки равны соответствующим линейным напряжениям генератора, т.е. система линейных напряжений и при несимметричной нагрузке симметрична. Включение нейтрального провода позволяет принудительно уравнять потенциалы нейтральных точек генератора и приемника. Следовательно, фазные напряжения потребителя равны соответствующим фазным напряжениям генератора, т.е. остается справедливым соотношение между фазными и линейными напряжениями приемника:  .При наличии нейтрального провода и несимметричной нагрузки геометрическая сумма векторов фазных токов трехфазной системы в соответствии с первым законом Кирхгофа для нейтральной точки равна току в нейтральном проводе:  .Векторная диаграмма для несимметричной активной нагрузки с нейтральным проводом имеет вид, представленный на рис. 3.6, а. Таким образом, нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке. Поэтому несимметричную нагрузку включают в четырехпроводную цепь, при этом режим работы каждой фазы нагрузки, находящейся под неизменным фазным напряжением, не будет зависеть от режима работы других фаз. Если сопротивлением нейтрального провода не пренебрегать, то при IN 0 (нагрузка несимметричная) напряжения на фазах нагрузки не будут равны соответствующим фазным напряжениям генератора. Между нейтральными точками генератора и нагрузки появится напряжение 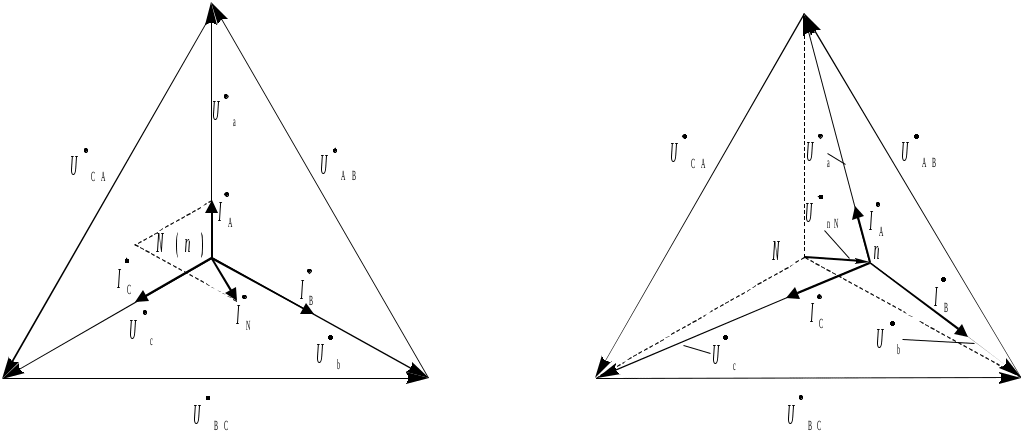 , называемое напряжением смещения нейтрали. На векторной диаграмме произойдет смещение нейтральной точки нагрузки (n) (рис. 3.6, б). a) б) Рис. 3.6. Векторная диаграмма токов и напряжений трехфазного несимметричного потребителя, схема соединения «звезда»: а - при наличии нейтрального провода; б - при отсутствии нейтрального провода Из рис. 3.3 видно, что при соединении звездой трехфазная система представляет собой электрическую цепь с двумя узлами – нейтральными точками N и n. Наиболее удобным методом расчета в данном случае является метод двух узлов. В соответствии с ним напряжение между нейтральными точками генератора и потребителя определяется по следующей формуле:  , (3.2)где  –– комплексные проводимости фаз потребителя и нулевого провода соответственно. Данное выражение позволяет учесть реальные, отличные от нуля сопротивления линейных и нейтрального проводов.Фазные напряжения генератора, приемника и напряжения смещения нейтрали связаны соотношениями, полученными по второму закону Кирхгофа (рис. 3.3):  .По определенным таким образом фазным напряжениям и используя приведенные выше соотношения (1), можно найти токи фаз потребителя, работающего в несимметричном режиме. При увеличении сопротивления нулевого провода эффективность его использования при несимметричной нагрузке уменьшается. В случае обрыва нейтрального провода значения фазных напряжений оказываются существенно зависящими от степени несимметричности нагрузки, т.е. от значений и характера сопротивлений различных фаз трехфазного потребителя. Так как сопротивления фаз могут изменяться в широких пределах, существенно могут изменяться и фазные напряжения. На одних фазах приемника напряжение может оказаться значительно больше, а на других меньше фазного напряжения сети  , т.е. того напряжения, на которое рассчитаны приемники. А это недопустимо. По этой причине предохранители не включают в нулевой провод.Рассмотрим два крайних случая несимметричного режима работы трехфазного потребителя без нейтрального провода: режим короткого замыкания и режим обрыва фазы. Для определенности предположим, что до возникновения несимметричного режима сопротивления фаз трехфазного потребителя были одинаковыми и активными: Ra = Rb = Rc = R. В случае короткого замыкания одной фазы потребителя электроэнергии (например, фазы «а», рис. 3.7, а), потенциал нейтральной точки приемника оказывается равным потенциалу начала фазы А генератора. Нейтральная точка n на векторной диаграмме (рис. 3.7, б) смещается в вершину треугольника линейных напряжений (А, а), соответствующую короткозамкнутой фазе. Фазное напряжение  . Напряжения на незакороченных фазах:  , т.е. увеличиваются до линейных напряжений. По этой причине токи IB и IС возрастают в  раз. Ток фазы A при этом  и превышает свою величину до возникновения режима короткого замыкания в три раза.Геометрическая сумма векторов всех трех фазных токов в этом случае также равна нулю. Отключение нагрузки одной из фаз в трехфазной системе (рис. 3.8, а) можно также рассматривать как частный случай несимметричной нагрузки, при которой сопротивление отключенной фазы равно бесконечности. Пусть имеет место обрыв фазы а. В этом случае комплексная проводимость фазы а:  , а проводимости двух других фаз одинаковы и активны:  . Подстановка проводимостей фаз в выражение для напряжения смещения нейтрали (2) дает . а) б) Рис. 3.7. Режим короткого замыкания: а - схема цепи; б - векторная диаграмма напряжений и токов 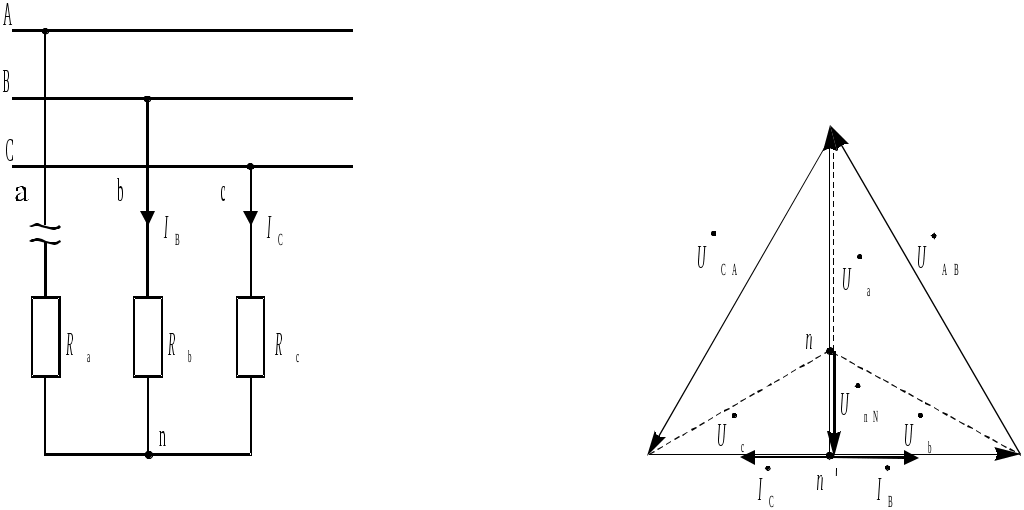 а) б) Рис. 3.8. Режим обрыва фазы: а - схема цепи; б - векторная диаграмма напряжений и токов Вектор  на рис. 3.8, б определяет положение, куда сместится нейтральная точка потребителя n в результате обрыва фазы. Фазное напряжение Ua увеличивается в 1,5 раза, а напряжения Ubи Uc уменьшаются в  раза, т.к. они становятся равными половине линейного напряжения. Ток в фазе а равен нулю, а токи в фазах b и c остаются равными друг другу по величине и уменьшаются в раза из-за уменьшения напряжений Ubи Uc.Схема соединения "треугольник" П 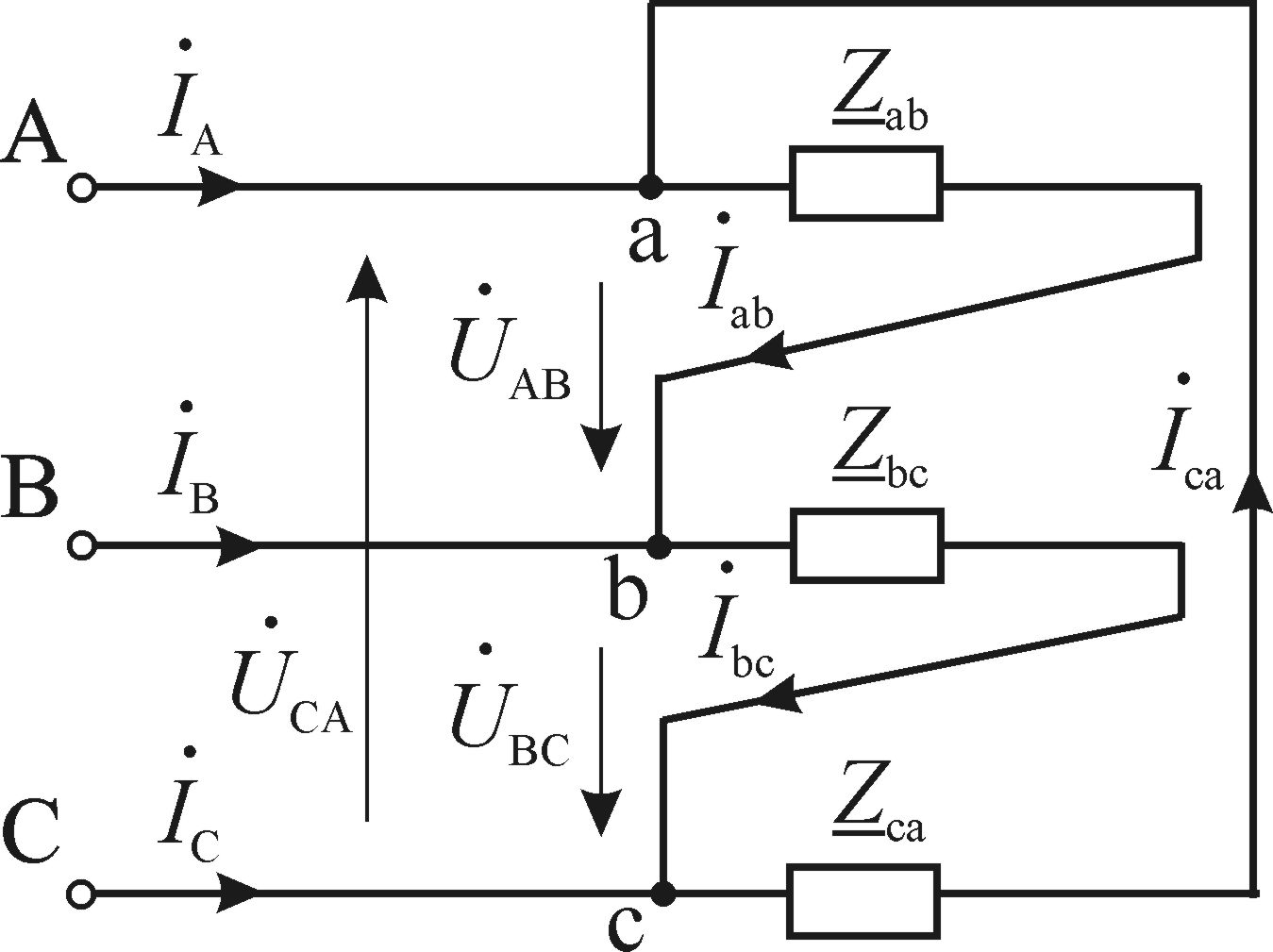 Рис. 3.9. Соединение фаз потребителя по схеме «треугольник» ри соединении по схеме “треугольник” конец предыдущей фазы соединяется с началом следующей фазы (рис. 3.9). Напряжения, токи и сопротивления фаз потребителя обозначаются индексами, соответствующими линиям, к которым подключается данная фаза. Независимо от значений и характера сопротивлений фаз приемника каждое фазное напряжение приемника равно соответствующему линейному:  . По величине фазные напряжения равны линейным Uфи Uл. Если не учитывать сопротивлений проводов сети, то напряжения приемника равны соответствующим напряжениям генератора. Соединение фаз потребителя треугольником следует применять в случае, когда номинальное напряжение каждой фазы приемника соответствует линейному напряжению сети.Из схемы рис. 3.9 видно, что фазные токи Iab, Ibc и Iсa в общем случае не равны линейным токам IA, IB и IC. Соотношение между линейными и фазными токами можно установить, применяя первый закон Кирхгофа для точек разветвления a, b и c:  (3.3)Из полученных выражений следует, что каждый вектор линейного тока равен разности векторов соответствующих фазных токов. Фазные токи при соединении потребителя "треугольником" определяются в соответствии с законом Ома:  .Углы сдвига по фазе между векторами фазных напряжений и соответствующими векторами фазных токов  определяются фазными сопротивлениями потребителя:ab = arctg(Xab/Rab); bс = arctg(Xbс/Rbс); сa = arctg(Xca/Rca). При симметричной нагрузке токи всех трех фаз будут равны между собой и векторы токов сдвинуты относительно соответствующих векторов линейных напряжений на одинаковые углы. Из векторной диаграммы для активно-индуктивной нагрузки, представленной на рис. 3.10, видно, что и линейные токи оказываются равными. Следует обратить внимание на то, что при построении векторной диаграммы для соединения потребителя треугольником вектор линейного напряжения  принято направлять вертикально вверх. Между фазными и линейными токами при симметричной нагрузке выполняется соотношение .Важной особенностью соединения фаз нагрузки треугольником является то, что при изменении сопротивления одной из фаз будут изменяться только ток данной фазы и линейные токи в проводах, соединенных с этой фазой. Так как линейные напряжения генератора постоянны, режимы работы других фаз останутся неизменными, поэтому схема соединения треугольником широко используется для включения несимметричной однофазной нагрузки, например, ламп накаливания. Векторная диаграмма, построенная для случая несимметричной активной нагрузки трехфазного потребителя при соединении треугольником, представлена на рис. 3.11.
Проведем анализ двух частных случаев несимметричной нагрузки трехфазного потребителя: обрыва фазы и обрыва линейного провода. В обоих случаях будем предполагать для определенности, что до возникновения несимметричных режимов работы потребителя сопротивления фаз были одинаковыми по величине и активными, т.е.: Rab = Rbc = Rca. При обрыве фазы ab фазный ток Iab = 0 (рис. 3.12, а). Другие фазные токи не изменились. Линейный провод B оказывается последовательно включенным с фазой bc, поэтому линейный ток  (3). На этом же основании  (с учетом взаимного направления токов IA и Ica). Таким образом, токи IA и IB уменьшаются в раз и становятся равными фазным токам. Ток линии C IС остается неизменным и определяется так же, как и в исходном режиме (1). Векторная диаграмма данного режима работы потребителя приведена на рис. 3.12, б.При обрыве одного из линейных проводов трехфазная цепь преобразуется в однофазную цепь. На рис. 3.13, а представлена схема трехфазной цепи с обрывом линейного провода С. Фазы приемника образуют две параллельные ветви, находящиеся под действием линейного напряжения UAB. Ток 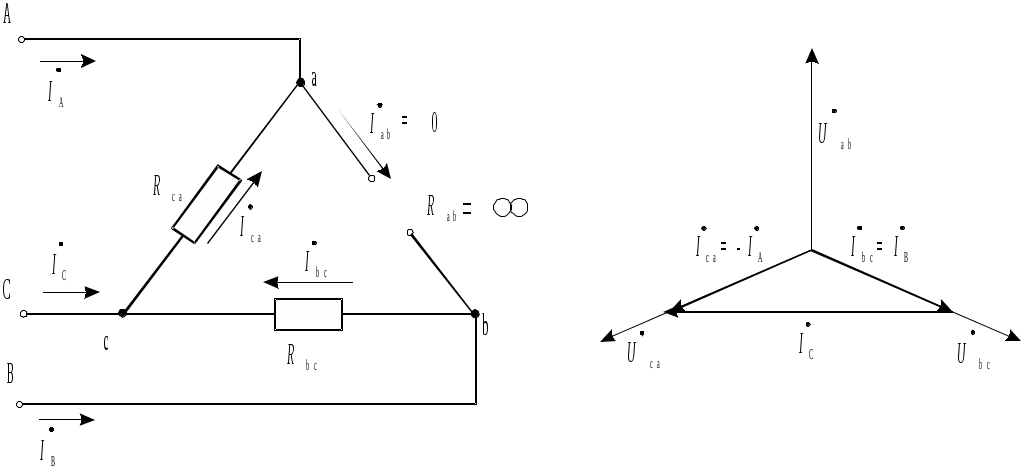 фазы ab не меняется, так как остается неизменным напряжение, приложенное к этой фазе. Фазы bc и ca соединены последовательно, поэтому их токи одинаковы (это фактически один и тот же ток) и совпадают по фазе с током  , так как определяются одним и тем же напряжением  . Линейный ток  совпадает по фазе с током , а по значению в 1,5 раза больше его. Векторная диаграмма токов и напряжений для данного режима представлена на рис. 3.13, б. а) б) Рис. 3.12. Соединение «треугольник», режим обрыва фазы: а - схема цепи; б - векторная диаграмма напряжений и токов Мощность трехфазного потребителя Мощности каждой фазы трехфазного потребителя определяются так же, как и при расчете однофазных цепей. Активная, реактивная и полная мощности фаз определяются из выражений: Pф = UфIфcosф; Qф = UфIфsinф; Sф = UфIф. При несимметричной нагрузке необходимо определять мощность каждой фазы в отдельности. Активная мощность трехфазного потребителя равна сумме активных мощностей фаз. С учетом принятых обозначений при соединении звездой активная мощность потребителя P = Pa + Pb + Pc = UaIAcosa + UbIBcosb + UcICcosc. При соединении треугольником P = Pab + Pbc + Pca = UabIabcosab + UbcIbccosbc + UcaIcacosca. Реактивная мощность трехфазного потребителя равна алгебраической сумме реактивных мощностей отдельных фаз. Для соединения звездой реактивная мощность Q = Qa + Qb + Qc = UaIAsina + UbIBsinb + UcICsinc. Реактивная мощность при соединении треугольником Q = Qab + Qbc + Qca = UABIabsinab + UBCIbcsinbc + UCAIcasinca. Реактивная мощность фазы будет положительной при индуктивном характере сопротивления фазы, а отрицательной – при емкостном. Полная мощность трехфазной цепи  .При симметричной нагрузке фазные напряжения, токи и углы сдвига фаз оказываются равными. Вследствие этого равны также активные, реактивные и полные мощности всех трех фаз потребителя электроэнергии. Мощность трехфазного потребителя всегда удобнее вычислять через линейные напряжение и ток, так как линейные величины всегда удобнее измерять. 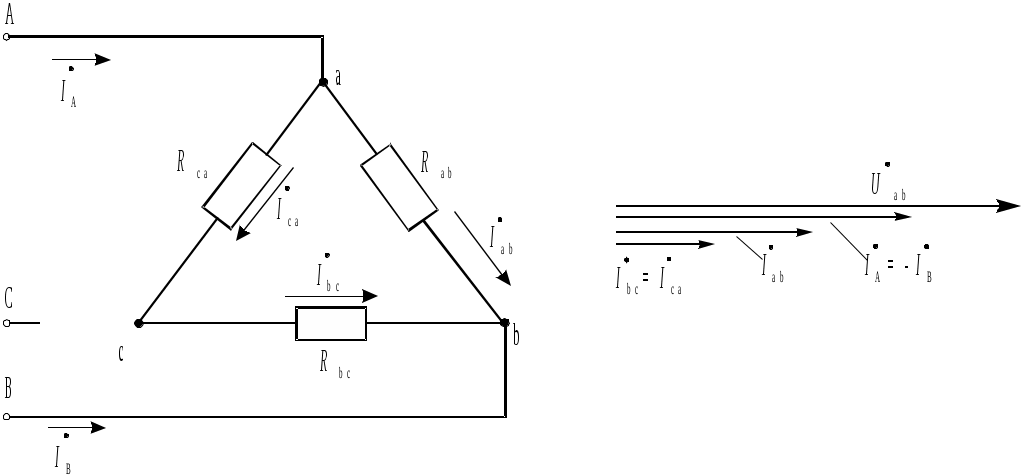 а) б) Рис. 3.13. Соединение «треугольник», режим обрыва линии: а - схема цепи; б - векторная диаграмма напряжений и токов Активная мощность симметричного трехфазного потребителя независимо от схемы его соединения может быть найдена через линейные токи и напряжения: P=3Pф=3UфIфcosф =  UЛIЛcosф.Аналогично можно получить и формулу для реактивной мощности симметричного трехфазного потребителя: Q = 3Qф = 3UфIф sin ф = UЛIЛsinф.При симметричном приемнике его полная трехфазная мощность  .Методические указания к выполнению работы1. Ознакомиться с основными теоретическими положениями и законами цепей трехфазного тока и ответить на контрольные вопросы. 2. Ознакомиться с лабораторной установкой (модуль питания, модуль трехфазного напряжения, модуль трехфазного трансформатора, измерительный модуль, модуль мультиметров, модуль резисторов). 3. Исследовать трехфазную цепь при соединении приемников электрической энергии звездой с нейтральным проводом. 4. Принципиальная схема цепи приведена на рис. 3.14, а. Собрать четырехпроводную трехфазную цепь по монтажной схеме, рис. 3.15. При сборке цепи следует придерживаться цветовой системы обозначений проводников: линия A – желтый, линия B – зеленый, линия С – красный, нейтральный провод – синий. 5. Мультиметры установить на измерение переменного напряжения (300 В). При измерении напряжений используются выводы мультиметров, отмеченные как «COM» и «V». Установить переключатели значений сопротивлений резисторов SA1, SA2, SA3 (модуль резисторов) в положения “∞”. 6. Установить на модуле трехфазного напряжения частоту питающего напряжения 50 Гц (потенциометр RP1 - в крайнее правое положение). Предъявить схему для проверки преподавателю и получить допуск к выполнению работы. 7. Включить модуль питания стенда (выключатель QF), модуль трехфазного напряжения (выключатель SA1и тумблер SA2, положение «Вперед») и модуль трехфазного трансформатора (выключатель QF1). 8. Установить в фазах потребителя одинаковые значения сопротивлений резисторов 50 Ом (симметричная нагрузка). Измерить токи, фазные и линейные напряжения. Напряжения измерять, подключая входы мультиметра к соответствующим гнездам. Результаты измерений занести в табл. 3.1. В несимметричном режиме сопротивление одного из резисторов уменьшить до 30 Ом. В режиме обрыва фазы сопротивление одного из резисторов установить в положение “∞”. Выключить модуль трехфазного трансформатора. 9. Разомкнуть цепь нейтрального провода (удалить соответствующий проводник). Включить модуль трехфазного трансформатора и провести измерения при отключенном нейтральном проводе. Обрыв фазы производить, установив сопротивление одного из резисторов в положение “∞”. Короткое замыкание производить, соединяя проводом начало и конец одного из резисторов. Результаты занести в табл. 3.2. Выключить модуль трехфазного трансформатора. 10. Исследовать трехфазную цепь при соединении потребителей электрической энергии треугольником. Принципиальная схема цепи приведена на рис. 3.14, б. Собрать цепь по монтажной схеме, рис. 3.16. Установить переключатели значений сопротивлений резисторов SA1, SA2, SA3 (модуль резисторов) в положения “∞”. Предъявить схему для проверки преподавателю и получить допуск к выполнению работы. 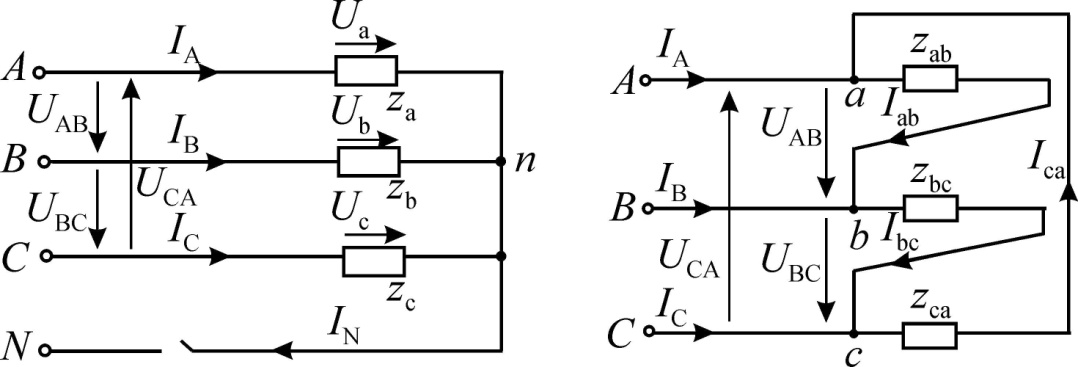 Рис. 3.14. Принципиальные схемы соединения фаз трехфазных потребителей: а - соединение по схеме «звезда», б - соединение по схеме «треугольник» 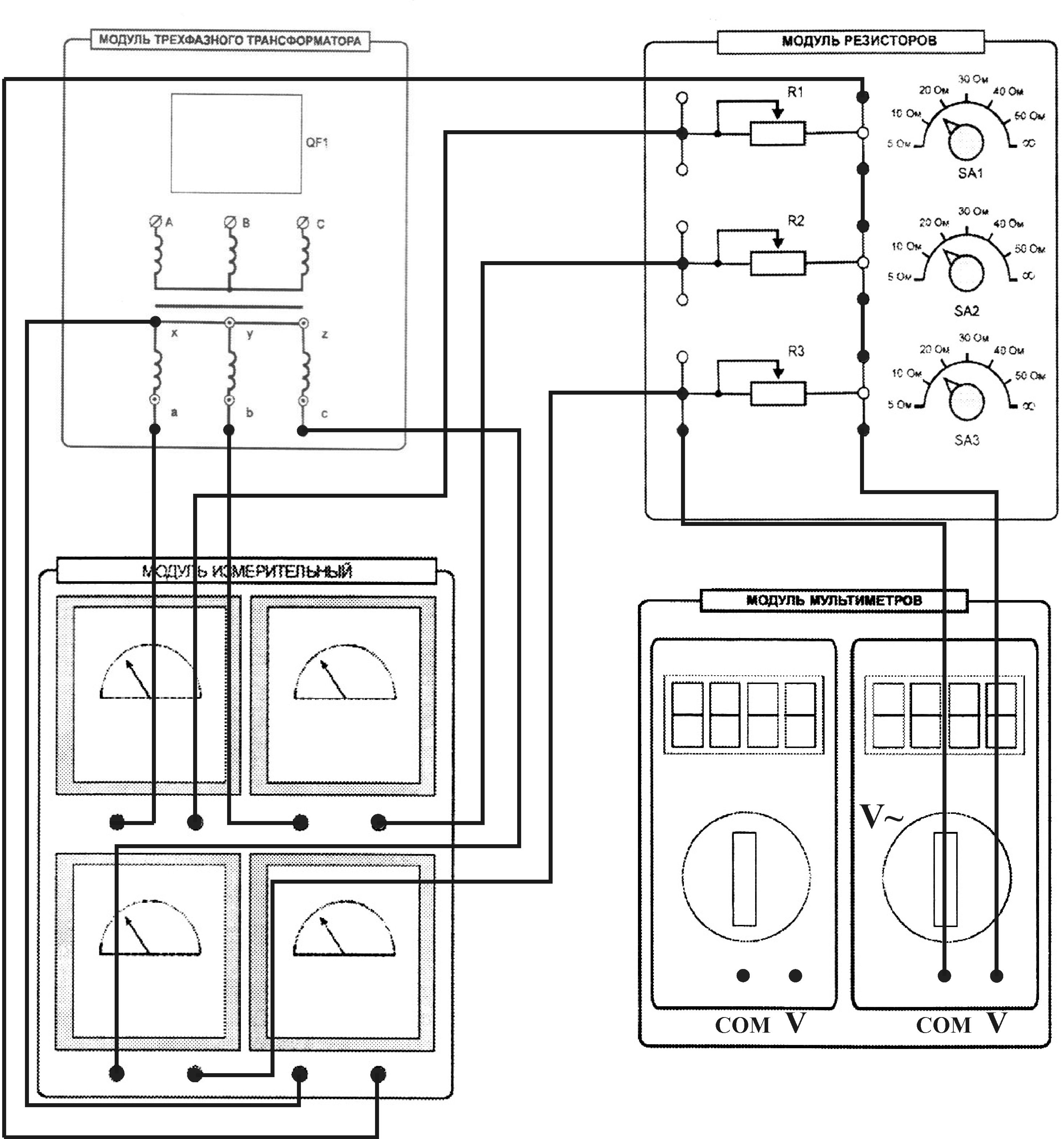 Рис. 3.15. Монтажная схема для сборки и исследования работы трехфазного потребителя, схема соединения «звезда» Таблица 3.1 Схема соединения "звезда с нейтральным проводом"
Таблица 3.2 Схема соединения "звезда без нейтрального провода"
11. Включить модуль трехфазного трансформатора (выключатель QF1). Установить в фазах потребителя одинаковые значения сопротивлений резисторов 50 Ом (симметричная нагрузка). Измерить фазные токи Iab, Ibc, Ica, линейный ток IA, линейные напряжения UAB, UBC, UCA. Напряжения измерять, подключая входы мультиметра к соответствующим гнездам. Результаты измерений занести в табл. 3.3. В несимметричном режиме сопротивление одного из резисторов уменьшить до 30 Ом. В режиме обрыва фазы сопротивление одного из резисторов установить в положение “∞”. 12. Выключить модуль трехфазного трансформатора (выключатель QF1), модуль трехфазного напряжения (тумблер SA2 и выключатель SA1), модуль питания стенда (выключатель QF). 13. Обработать результаты измерений по пп. 7, 8 и 10: 14. Рассчитать мощности отдельных фаз Pф = IфUф и общую мощность  для соединения "звезда" с нейтральным проводом (табл. 3.1). Сравнить вычисленные значения с результатами измерений. 15. Величины линейных токов IB, IC (табл. 3.3) определяются по первому закону Кирхгофа (графически). 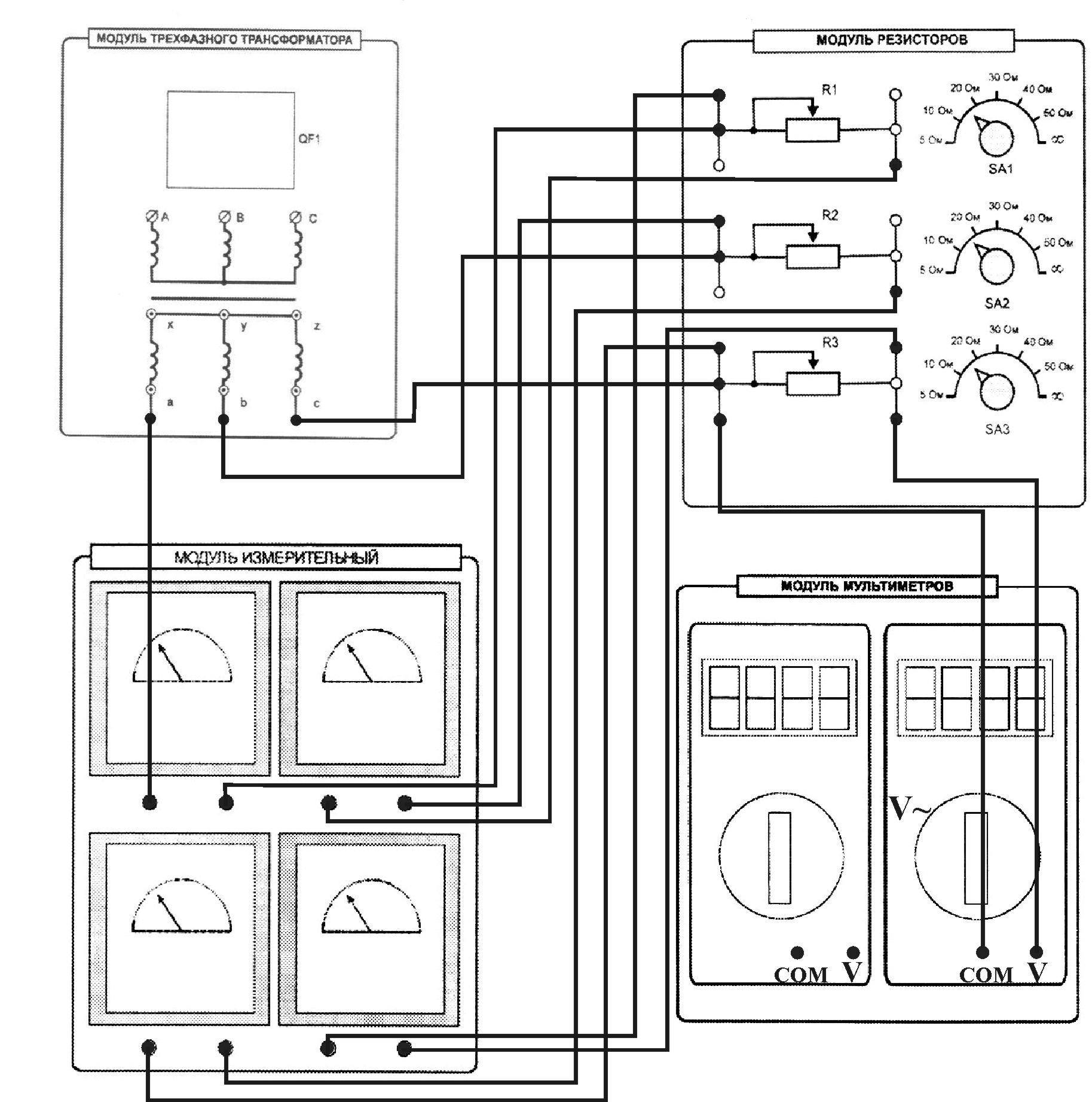 Рис. 3.16. Монтажная схема для сборки и исследования работы трехфазного потребителя, схема соединения «треугольник» 16. Определить соотношения между фазными и линейными значениями напряжений (пп. 7, 8), а также фазными и линейными значениями токов (п. 10) для симметричных режимов; внести эти соотношения в соответствующие таблицы. 17. По данным измерений табл. 3.1, табл. 3.2 и 3.3 построить в масштабе совмещенные векторные диаграммы напряжений и токов. Таблица 3.3 Схема соединения "треугольник"
Контрольные вопросы1. Какие цепи называются трехфазными? 2. Чем была вызвана необходимость разработки трехфазных цепей и почему они получили широкое практическое применение? 3. Приведите способы изображения симметричной системы ЭДС трехфазного генератора. 4. Укажите соотношения между фазными и линейными напряжениями. 5. В чем преимущество четырехпроводной трехфазной цепи? 6. Какова роль нейтрального провода? Почему в нейтральный провод не включают предохранители? 7. Что такое напряжение смещения нейтрали? Как его определяют? 8. В каких случаях применяют трехпроводные цепи? 9. Как определяют фазные и линейные токи при соединении приемников треугольником? 10. Укажите соотношения между фазными и линейными токами. 11. Как выбрать схему включения приемника в трехфазную сеть? 12. Как выражается активная, реактивная и полная мощности трехфазных приемников (симметричных и несимметричных)? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
