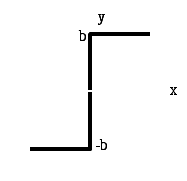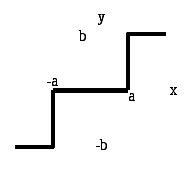дз по тау. Домашнее задание по ТАУ (часть2). Исследование релейной системы на фазовой плоскости
 Скачать 98.5 Kb. Скачать 98.5 Kb.
|
|
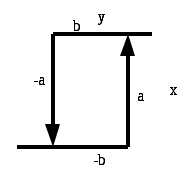
Домашнее задание часть II. Исследование релейной системы на фазовой плоскости. Нелинейная система при наличии одного нелинейного элемента может быть структурно представлена как одноконтурная система, состоящая из последовательно включенных безынерционного нелинейного элемента и линейной части с передаточной функцией Wлч (р). НЭ Wлч(р)      _ _ Рис. 1. Если линейная часть описывается дифференциальным уравнением второго порядка, то для исследования таких систем удобно применить метод фазовой плоскости. По оси абсцисс на фазовой плоскости откладывается значение переменной х (обычно отклонение регулируемой величины от заданного значения) и скорость ее изменения y = dx / dt . Состояние системы регулирования в каждый момент времени определяется значениями х и у и, следовательно, может быть охарактеризовано положением изображающей точки М на фазовой плоскости. Совокупность фазовых траекторий составляет фазовый портрет системы, дающий общее представление о характере движения системы. В данной лабораторной работе исследуются нелинейные системы второго порядка с различными видами релейных характеристик, показанных на рисунках 2а, 2б и 2в.
Рис. 2. Релейные характеристики: Для релейных систем движения могут быть разбиты на отдельные участки, каждый из которых описывается собственным линейным уравнением. Затем фазовые траектории, построенные отдельно для каждого участка, можно соединить (припасовать) друг с другом в местах стыковки (в линиях переключения). При построении фазовых траекторий следует руководствоваться следующими правилами. При у 0 изображающая точка движется слева направо, а при у 0, наоборот, справа налево. При у = 0, т.е. при нулевой скорости изменения координаты, траектории пересекают ось х под прямым углом. Фазовые траектории не пересекаются между собой ни в одной точке, за исключением особых точек. Порядок выполнения задания. Линейная часть системы задается в виде передаточных функций: а) Параметры нелинейностей, вид передаточной функции и ее коэффициенты задаются преподавателем. Для выполнения задания используется программа PHASPL "Исследование нелинейной системы 2-го порядка". пакета ТАУ. Задание выполняется в следующей последовательности. В главном меню выбирается пункт "Выбор управления" и устанавливается "Релейное управление". В главном меню выбирается пункт "Задание параметров объекта", в котором находят заданный вид передаточной функции и вводят коэффициенты. В главном меню выбирается пункт "Выбор НЭ", в котором находят нужный вид нелинейного элемента и вводят его параметры. После ввода коэффициентов передаточной функции и выбора нелинейности нужно перейти в пункт главного меню "Фазовый портрет", где предварительно задаются начальные условия х0 и у0 Для получения характерного вида кривых рекомендуется устанавливать примерно следующие значения начальных условий.
При заданных начальных условиях программа PHASPL строит на экране монитора фазовую траекторию и показывает линии переключения. Для построения второй и последующих траекторий на первом графике с помощью курсора вводят новые значения начальных условий и нажимают кнопку "Пуск". Полученный фазовый портрет распечатывается. Содержание отчета. В отчете должны быть приведены фазовые портреты для каждой нелинейности. Отразить, как движется изображающая точка по фазовым траекториям. Необходимо записать дифференциальные уравнения связи входа и выхода для каждого участка нелинейного элемента, дифференциальные уравнения фазовых траекторий, исключив время t. При наличии предельного цикла определить амплитуду автоколебаний. При защите домашнего задания необходимо знать: определение фазового пространства и фазовой плоскости; как получить уравнения фазовых траекторий; что такое особые точки на фазовой плоскости; предельные циклы. Устойчивый и неустойчивый предельный цикл, какой предельный цикл получен в каждом из случаев; уметь качественно нарисовать переходный процесс по фазовой траектории. |