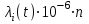Автоматизация управления мокрого помола сырьевых материалов при производстве цемента. Работа. Исследование случайных процессов при автоматизации
 Скачать 340.23 Kb.
|
 Рисунок 2-Функциональная схема автоматизации 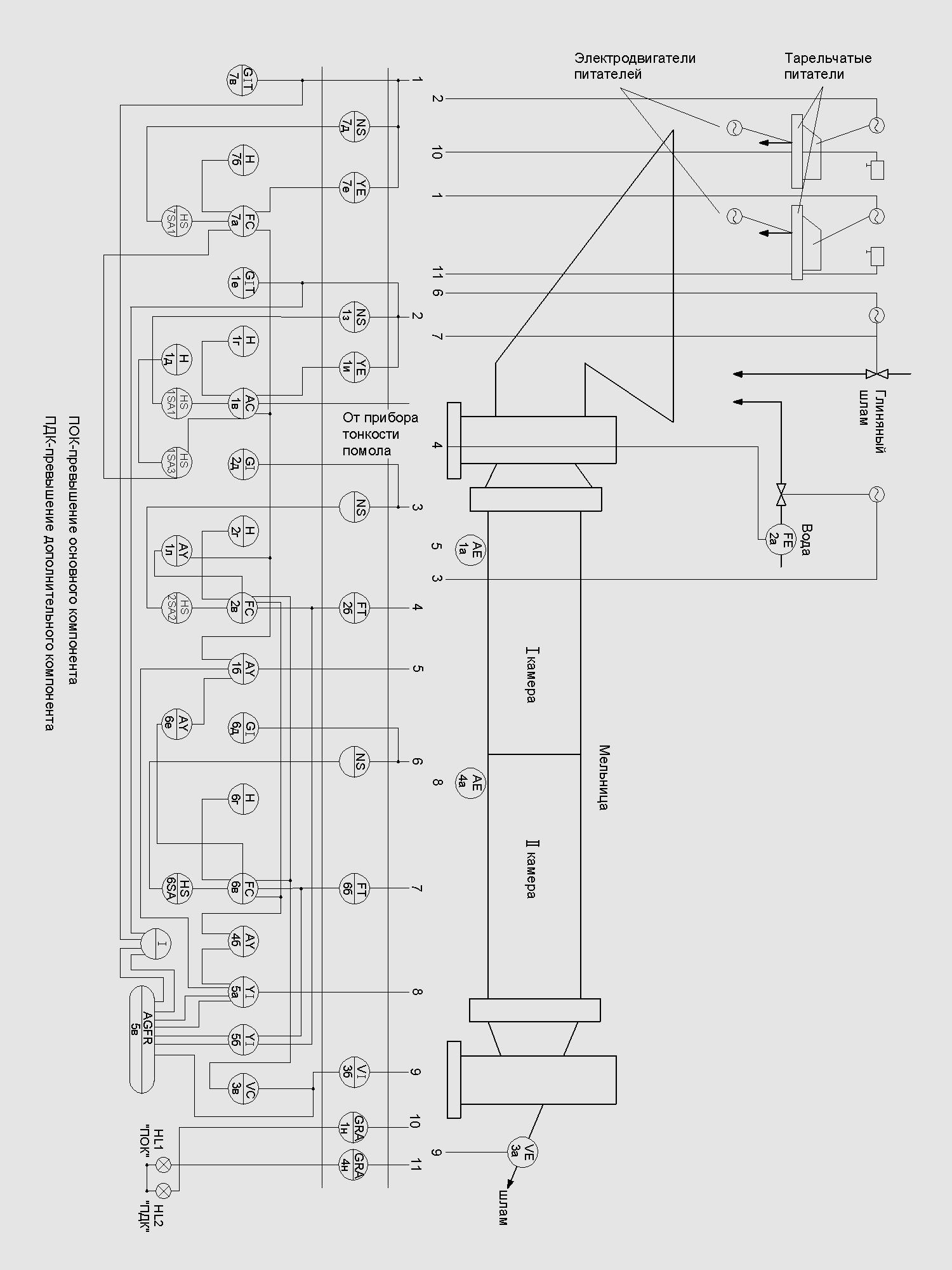 3 РАСЧЕТ НАДЕЖНОСТИ СХЕМЫ АВТОМАТИЗАЦИИ Под надежностью схемы понимается ее способность безукоризненно выполнять свои функции в течение определенного времени в заданных режимах работы. Она является главным требованием к схеме. Надежность включает в себя следующие качественные показатели: 1 Безотказность-свойство изделия сохранять свою работоспособность в течение некоторого времени. 2 Ремонтопригодность - приспосабливаемость изделия к обнаружению и устранению неисправностей. 3 Долговечность-способность объекта сохранять работоспособность до наступления предельного состояния. 4 Сохранность-это свойство объекта непрерывно находиться в исправном состоянии при хранении и транспортировании. Количественной характеристикой надежности являются отказы, вероятность безотказной работы, интенсивность отказов и наработка на отказ. Отказ это нарушение работоспособности изделия. Отказы делятся на: 1 Полный отказ. При его возникновении работа невозможна до полного устранения отказа. 2 Частичный отказ. Связан с ухудшением одной из характеристик. 3 Внезапный отказ. В результате скачкообразного изменения, какого-либо параметра (короткого замыкания). 4 Постепенный отказ. Параметры системы постепенно выходят из допустимых пределов. 5 Зависимый отказ. Возникает в системе из-за отказа другого элемента. Требования надежности обеспечиваются: 1 Применением надежных приборов. 2 Оптимальными режимами работы. 3 Резервированием наиболее ответственных цепей схемы. 4 Автоматизированным контролем за неисправностью схемы. 5 Запретными блокировками. 6 Сокращением времени нахождения элементов в схеме под напряжением. Количественные характеристики расчета надежности: Р(t) - вероятность безотказной работы. Это вероятность того, что в пределах заданного времени отказа не возникнет. Величина безразмерная. λ(t) - интенсивность отказов, т.е. частота отказов в системе в единицу времени. Измеряется в единице, деленной на час или час в минус первой степени. То - наработка на отказ. Ожидаемое время работы до отказа элемента или системы. Интенсивность отказа рассчитывается по формуле: 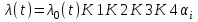 , (1)где λ(t) - интенсивность отказа одного прибора, выбирается по таблице. 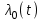 - интенсивность отказа табличная.К1 – коэффициент, зависящий от вибрации. К2 – коэффициент, зависящий от ударной нагрузки. К 3 - коэффициент, зависящий от температуры и влажности. К 4 - коэффициент, зависящий от давления. άi – коэффициент, зависящий от загрузки оборудования. Общая интенсивность отказа схемы рассчитывается по формуле: 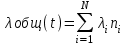 , (2)где 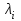 -интенсивность отказов элемента в данных условиях эксплуатации.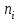 - количество элементов с . 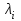i - количество разновидностей элементов по типам.Таблица 1 Коэффициенты, зависящие от вибрации и удара
Таблица 2 Коэффициент, зависящий от температуры
Таблица 3 Коэффициент, зависящий от давления
Влияние загрузки оборудования оценивается по коэффициенту загрузки άi Для загрузки оборудования от 10% до 100% άi = 0,25 ... 1 Таблица 4 Влияние загрузки оборудования
Приняты стационарные условия, при которых К1 = 1,04; К2 = 1,03 Стационарные условия подходят к условиям эксплуатации рекуператоров, а именно учитывают воздействия вибрации к ударной нагрузке в закрытом помещении на заводе. Принято значение влажности 60-70%, и значение температуры 20-40 °С при которых КЗ = 1,0.Принята высота над уровнем моря от 0 до 1 км., что применимо к Воронежской области. Для удобства упрощения расчёта найдено произведение коэффициентов (формула 3) К = К1 • К2 • КЗ • К4 (3) К=1,04•1,03•1,0•1,00=1,07 На основании выбранных приборов заполнена таблица для расчёта надёжности Таблица 5 Сводные данные для расчета надежности схемы автоматизации
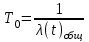 (4)Таблица 6 К расчету надежности. Значения λio 10-6 1/ч
λi1(t)=0,35•10-6•1,07•1,00=0,02•10-6(ч) λi2(t)= 1,80•10-6•1,07•0,35 =0,67•10-6(ч) λi3(t)=1,30•10-6•1,07•0,35=0,48•10-6(ч) λi4(t)=1,34 •10-6•1,07•0,25=0,35•10-6(ч) λi5 (t) =1,80•10-6•1,07•0,35=0,67•10-6(ч) λi6(t)=0,12 •10-6•1,07•1,00=0,12•10-6(ч) λi7(t)=0,24•10-6•1,07•0,25=0,06•10-6(ч) λi8(t)=0,34 •10-6•1,07•0,25=0,09•10-6(ч) λi9(t)=0,54 •10-6•1,07•1,00=0,57•10-6(ч) λi10(t)=0,12•10-61,07•1,00=0,12•10-6(ч) λi11(t)=0,015 •10-6•1,07•1,00=0,01•10-6(ч) λi1общ.(t)=0,02•10-6•6=0,14•10-6(ч) λi2общ.(t)=0,67•10-6•5=3,37•10-6(ч) λi3общ.(t)=0,48•10-6•8=3,89•10-6(ч) λi4общ.(t)=0,35•10-6•5=1,79•10-6(ч) λi5общ.(t)=0,67•10-6•10=6,74•10-6(ч) λi6общ(t)=0,12 •10-6•5=0,64•10-6(ч) λi7общ.(t)=0,06 •10-6•4=0,25•10-6(ч) λi8общ.(t)=0,09 •10-6•2=0,18•10-6(ч) λi9общ.(t)=0,57 •10-6•4=2,31•10-6(ч) λi10общ.(t)=0,12 •10-6•2=0,24•10-6(ч) λi11общ.(t)=0,01 •10-6•1=0,01•10-6(ч) λiобщ.(t)=(0,14+3,37+3,89+1,79+6,74+0,64+0,25+0,18+2,31+0,24+0,01) • *10-6=19,59•10-6(ч) p(t)100=1-19,59•10-6•100=0,999 p(t)1000=1-19,59•10-6•1000=0,99 p(t)10000=1-19,59•10-6•10000=0,1 T0=1/19,59  10-6=51 103 (ч)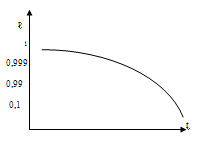 Рисунок 3 - График зависимости вероятности безотказной работы от времени Вывод: Данная система является надёжной, так как наработка на отказ (Т0) составляет 5,2 лет 4. ИССЛЕДОВАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ ПРИ АВТОМАТИЗАЦИИ В практике производства цемента существуют сложные технологические объекты - шаровые мельницы. Разработка систем автоматического регулирования для этого агрегата представляет значительные трудности, т.к. надо знать показатели, наиболее полно характеризующие протекание тех. процесса и связь их между собой. Кроме того, при рассмотрении динамических характеристик объектов считалось, что возмущающие воздействия носят определенный (детерминированный) характер и имеет форму ступенчатого, прямоугольного сигнала. Но в промышленных условиях объекты регулирования непрерывно находятся под воздействием разнообразных возмущений. В таких случаях для анализа линейных систем используется аппарат теории случайных процессов. Случайным процессом называется процесс изменения случайной величины во времени. Случайной величиной называется величина, значение которой не может быть точно предсказано и которая меняется в зависимости от случая. Вместо термина "случайный" обычно используют понятия стохастический и вероятностный. Математическим ожиданием величины Y называется среднее значение случайной величины Y, определенное по множеству ее возможных значений. m=M(Y) , (5) где М – среднее значение случайной величины Математическое ожидание |
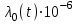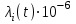ч
ч