Автоматизация управления мокрого помола сырьевых материалов при производстве цемента. Работа. Исследование случайных процессов при автоматизации
 Скачать 340.23 Kb. Скачать 340.23 Kb.
|
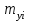 = =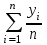 , (6) , (6)где 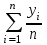 - сумма всех значений случайной величины при всем количестве наблюдений, - сумма всех значений случайной величины при всем количестве наблюдений,n – число наблюдений. Дисперсией называется среднее значение квадрата отклонения случайной величины Y от среднего значения. 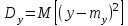 , (7) , (7)где 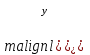 - математическое ожидание, - математическое ожидание,у – случайная величина. Среднеквадратичным отклонением называется величина, характеризующая среднюю изменчивость изучаемого свойства объекта. 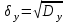 (8) (8)Среднеквадратичное отклонение 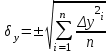 , (9) , (9)где 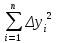 - сумма квадратов отклонений всех значений параметра от среднего арифметического - сумма квадратов отклонений всех значений параметра от среднего арифметическогоn – число наблюдений, знаки + и - показывают, что отклонения могут быть в ту и другую сторону от среднего значения. Для оценки точности результата измерения можно воспользоваться вероятной погрешностью. Вероятная погрешность результата измерений, т.е. среднего арифметического значения при нормальном законе распределения случайных погрешностей равна 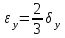 (10) (10)Такой способ определения справедлив только при большом количестве измерений, n 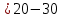 На практике число измерений может быть меньше. Поэтому определяют доверительный интервал. Используют коэффициенты Стьюдента 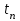 , которые зависят от доверительной вероятности Р и количества измерений n. , которые зависят от доверительной вероятности Р и количества измерений n.Для определения доверительного интервала среднюю квадратичную погрешность 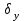 надо умножить на коэффициент стьюдента надо умножить на коэффициент стьюдента 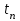 . .Окончательный результат измерения можно записать так : 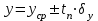 (11) (11)Тонкость помола влияет на скорость схватывания и твердения, а так же на прочность затвердевшего цемента: чем тоньше измельчен цементный клинкер, тем быстрее и полнее протекает взаимодействие цемента с водой и тем выше будет его прочность. Тонкость помола устанавливается ситовым анализом. Мы провели такой анализ. При этом получены результаты: Р1=2800 см2/г Р2=2850 см2/г Р3=2900 см2/г Р4=2800 см2/г Нужно определить интервал, в котором находится значение измеряемого параметра с доверительной вероятностью Р=0,99 РЕШЕНИЕ: 1.Находим среднее значение Р 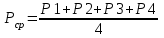 (12) (12)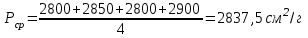 2.Находим остаточные погрешности измерений ρ 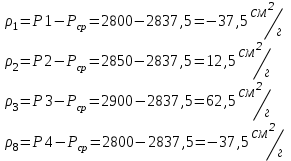  3.Находим среднеквадратичную погрешность измерений 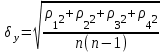 (13) (13)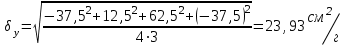 4.По таблице 7 находим для Р=0,99 и n=4 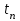 =5,8 =5,85.Тогда искомое значение параметра будет иметь вид Р=2837,5 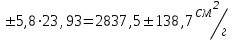 Таблица 7 Коэффициенты Стьюдента t
5. РАЗРАБОТКА СТРУКТУРНОЙ СХЕМЫ АСР ДЛЯ ОДНОГО КОНТУРА РЕГУЛИРОВАНИЯ Любая автоматическая система состоит из отдельных связанных между собой элементов. С точки зрения функциональных задач, выполняемых элементами в системе, их можно разделить на воспринимающие, задающие, сравнивающие, преобразующие, исполнительные и корректирующие. Воспринимающие элементы датчики измеряют физические параметры объекта регулирования и преобразуют их в электрический сигнал. Задающие элементы задатчики служат для задания требуемого значения регулируемого параметра. Сравнивающие элементы (СЭ) сопоставляют заданное значение управляемой величины с действительным значением параметра объекта регулирования. Полученный на входе СЭ сигнал рассогласованияпередается через усилитель на исполнительный механизм, который, в свою очередь, управляет регулирующим органом. Этот РО управляет состоянием объекта ОР. Корректирующие элементы служат для улучшения качества процесса управления. Эти элементы могут устанавливаться как после усилителя, так и после датчика. Кроме этой подробной структурной схемы системы в автоматике применяется упрощенная схема, которая состоит из крупных функциональных блоков. Наиболее крупным блоком является регулятор, который объединил сравнивающее устройство, усилитель, корректирующие элементы. Все элементы автоматики независимо от их назначения обладают определенной совокупностью характеристик и параметров, которые определяют их эксплуатационные и технологические особенности. Основной характеристикой является статическая характеристика элемента. Она представляет собой зависимость выходной величины Y от входной Х. Нужно составить АСР, структурная схема, которой представлена на приведённом ниже рисунке 4. 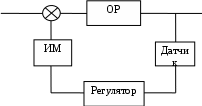 Рисунок 4-Структурная схема АСР И теперь мы можем составить один контур регулирования для функциональной схемы автоматизации цементной мельницы. 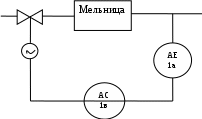 Рисунок 5 - Контур регулирования 6 РАСЧЕТ УСТОЙЧИВОСТИ АСР Все элементы автоматики независимо от их назначения обладают определенной совокупностью характеристик и параметров, которые определяют их эксплуатационные и технологические особенности. Основной характеристикой является статическая характеристика элемента. Она представляет собой зависимость выходной величины Y от входной Х в установившемся режиме. Y=f(x). Если исключить из рассмотрения все нелинейности, присущие этим характеристикам, то можно описать элементы автоматики линейными характеристиками. 1)Статическая характеристика ОР описывается уравнением  или или 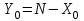 (14) (14)В соответствии с вариантом N = 2 Достаточно определить 2 точки, чтобы построить характеристику ОР Таблица 8 Построение характеристики ОР
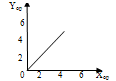 Рисунок 6 – Статическая характеристика ОР 2)Статическая характеристика датчика описывается уравнением 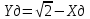 Для построения этой статической характеристики выбраны следующие значения Таблица 9 Построение характеристики датчика
По этим точкам построена прямая на рисунке 6 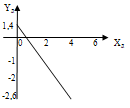 Рисунок 7 - Статическая характеристика датчика 3) Статическая характеристика регулятора описывается уравнением  (16) (16)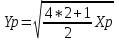 Таблица 10 Построение характеристики регулятора
По этим точкам построена прямая на рисунке 7 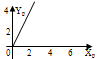 Рисунок 8 - Статическая характеристика регулятора 4) Статическая характеристика исполнительного механизма описывается уравнением  (17) (17)Достаточно определить 2 точки, чтобы построить характеристику исполнительного механизма Таблица 11 Построение характеристики исполнительного механизма
По этим точкам построена прямая на рисунке 8 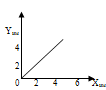 Рисунок 9 - Статическая характеристика исполнительного механизма 5) Для определения общей статической характеристики цепи ОС – ДРИМ изобразим статические характеристики этих звеньев на общей плоскости. В первом квадранте находится статическая характеристика датчика, во втором – регулятора, в третьем – исполнительного механизма. 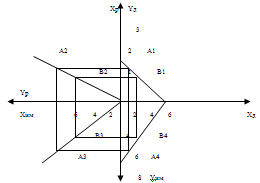 Рисунок 10 - Статическая характеристика цепи ОС-ДРИМ 6) Для определения взаимосвязи между статическими характеристиками ОР и ДРИМ изобразим их в одной системе координат. В результате эти две статические характеристики пересекутся в точке А. 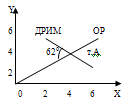 Рисунок 11 - Статические характеристики ОР и ДРИМ 7) Эта точка А называется рабочей . Угол пересечения этих прямых равен 620. Из теории АСР известно: при пересечении двух статических характеристик под углом 60-90° система характеризуется хорошей устойчивостью. 7. РАСЧЕТ КАЧЕСТВА ПЕРЕХОДНОГО ПРОЦЕССА Частотный критерий Михайлова. Этот частотный критерий позволяет судить об устойчивости замкнутой системы по поведению ее характеристического вектора на комплексной плоскости. Характеристический вектор получают путем подстановки в выражение для характеристического полинома значения p=iω. На рисунке представлены входные и выходные величины в виде векторов на комплексной плоскости. 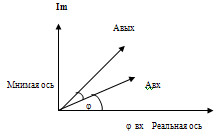 Рисунок 13 - Представление входных и выходных величин в виде векторов на комплексной плоскости Важную роль при описании линейных систем играют частотные характеристики, характеризующие реакцию объекта или звена на входной гармонический сигнал. Входная величина произвольной формы X(t) может быть представлена в виде суммы бесконечного числа синусоидальных колебаний, отличающихся амплитудами, частотой и фазой. Если система линейна, то выходная величина Y(t) равна сумме гармонических колебаний, каждое из которых является реакцией системы на соответствующую гармонику на входе. Функции частот (ω), описывающие изменения амплитуды и фазы гармонических колебаний при прохождении через линейную систему, называются частотными характеристиками системы. Амплитудно-частотная характеристика (АЧХ) – это зависимость отношения амплитуды на выходе к амплитуде колебаний на входе от частоты. 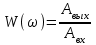 (21) (21)Фазочастотная характеристика (ФЧХ) – это зависимость разности фаз между выходными и входными гармоническими колебаниями от частоты. 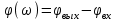 (22) (22)На рисунке показано прохождение установившихся гармонических колебаний через линейную систему. 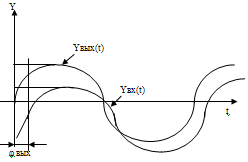 Рисунок 14 - Прохождение установившихся гармонических колебаний через линейную систему. Если в уравнении W(p) заменить p на iω , то получим характеристический вектор W(iω). При изменении ω от 0 до ∞ конец вектора W(iω) в комплексной плоскости вычертит кривую, называемую характеристической кривой или годографом. По виду годографа можно судить об устойчивости системы. По заданию был сделан расчёт устойчивости АСР, у которой передаточная функция 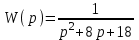 1.Построение годографа начинается с замены p на iω. 2.Получим частотную передаточную функцию 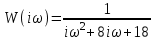 Умножим числитель и знаменатель на сопряженное значение знаменателя 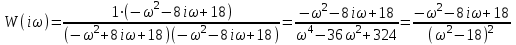 3.Выделим в этом выражении действительную Re(ω) и мнимую Im(ω) составляющие. Получим 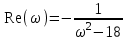 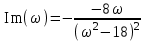 4.Построение годографа начинается с определения положения двух крайних точек ω=0 и ω=∞ При ω=0 Re(0)=0,05 Im(0)=0 Получим т.А на действительной оси При ω=∞ Re(∞)=0 Im(∞) 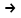 0 Получим т. В на действительной оси 0 Получим т. В на действительной оси5. Re=0 Im=- 8 Получим т.С, где частота 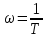 6. Пусть Re=0,05 Тогда Im=0,01 Получим т.Д 7. Соединим все точки А  В В С С Д и получим Д и получим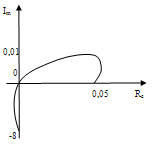 Рисунок 15 – Годограф статического объекта Сформулируем частотный критерий Михайлова: Для устойчивости системы необходимо и достаточно, чтобы ее характеристический вектор при изменении частоты от0 до +∞ повернулся в положительном направлении (против часовой стрелки) начиная с положительной вещественной части на число квадрантов, равное порядку характеристического уравнения (n). Т. к порядок характеристического уравнения равен 2 и вектор на рисунке повернут в положительном направлении на 2 квадранта, то система является устойчивой. 8 ВЫБОР ПРИБОРОВ И ОБОРУДОВАНИЯ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
