Физика твердого тела, ИССЛЕДОВАНИЕ ТЕНЗОЭФФЕКТА В КРЕМНИИ. 9283_Дмитриев_4_фтт_01. Исследование тензоэффекта в кремнии
 Скачать 72.22 Kb. Скачать 72.22 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина) Кафедра МНЭ отчёт по лабораторной работе №4 по дисциплине «Физика твёрдого тела» Тема: ИССЛЕДОВАНИЕ ТЕНЗОЭФФЕКТА В КРЕМНИИ
Санкт-Петербург 2021 Цель работы. Исследование тензоэффекта в кремнии Основные теоретические положения. Изменение удельного сопротивления кристалла при его деформации называется тензоэффектом. На практике деформация кристалла осуществляется посредством воздействия на него внешней нагрузки, прикладываемой в заданном кристаллографическом направлении. Всякая деформация кристалла сопровождается появлением в нем механических напряжений. Рассматривая тензор удельного сопротивления ρik как функцию тензора напряжений Pik, разложим его в ряд по степеням Рiк и ограничимся линейным членом ρik = ρik(0) + 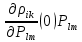 Первый член в этом разложении р, (0) представляет собой тензор удельного сопротивления недеформированного кристалла р.к, а второй - его изменение при деформации ∆ρik = ρik - ρik(0) = 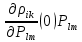 Как правило, интерес представляет не абсолютное значение ∆ρik, а относительное изменение ρik. Для этого определим среднее значение удельного сопротивления недеформированного кристалла в виде ρср0 = (1/3)(ρ110 + ρ220 + ρ330) Разделив левую и правую части уравнения на ρср0, получим следующее материальное уравнение, описывающее тензоэффект в кристаллах 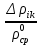 = πiklm = πiklm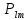 Тензор четвертого ранга πiklm = 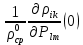 называется тензором пьезосопротивления. Так как ρik = ρki и называется тензором пьезосопротивления. Так как ρik = ρki и 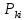 = = 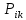 этот тензор обладает следующей симметрией относительно перестановки индексов: πiklm = πkilm = πikml. Отсюда следует, что тензор пьезосопротивления в общем случае определяется 36 независимыми величинами. Симметрия накладывает дополнительные ограничения на число независимых и неравных нулю компонентов этого материального тензора. В частности, в кристаллах кубической сингонии (в кристаллографической системе координат) они определяются всего тремя независимыми компонентами – π11, π12 и π44 этот тензор обладает следующей симметрией относительно перестановки индексов: πiklm = πkilm = πikml. Отсюда следует, что тензор пьезосопротивления в общем случае определяется 36 независимыми величинами. Симметрия накладывает дополнительные ограничения на число независимых и неравных нулю компонентов этого материального тензора. В частности, в кристаллах кубической сингонии (в кристаллографической системе координат) они определяются всего тремя независимыми компонентами – π11, π12 и π44π11 = π1111 = π2222 = π3333 π12 = π1122 = π1133 = π2211 = π2233 = π3311 = π3322, π44 = π1212 = π1221 = π2112 = π2121 = π1313 = = π1331 = π3113 = π3131 = π2323 = π2332 = π3223 = π3232 Рассмотрим стержень, вырезанный из кристалла, с осью, направленной вдоль единичного вектора n. Под действием однородной внешней нагрузки, действующей вдоль n, стержень может растягиваться или сжиматься. Если P - сила, действующая на единицу площади основания стержня, то тензор механических напряжений в кристалле определяется как 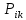 = Pnink = Pninkгде P > 0 соответствует растяжению стержня, P < 0 - сжатию Согласно закону Гука напряжение и деформация в кристалле связаны соотношением Pik = Ciklmulm где ulm тензор деформации, Ciklm - тензор модулей упругости. Последний обладает следующей симметрий относительно перестановки индексов Ciklm = Ckilm = Cikml - Clmik Таким образом, в общем случае имеет место всего 21 независимая составляющая этого тензора. В кубических кристаллах только три упругие постоянные, С11, С12 и С44, определяют все неравные нулю компоненты этого тензора C11 = C1111 = C2222 = C3333. C12 = C1122 – C1133 - C2211 - C2233 - C3311 = C3322 - C44 - C1212 - C1221 - C2112 = C2121 = C1313 = = C1331 = C3113 = C3131 - C2323 = C2332 - C3223 = C3232 Обработка результатов эксперимента. 1-2) Δ=3,25 мм L=235мм 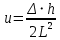 Таблица 1 – Результаты расчёта для образца 1
Таблица 3 – Результаты расчёта для образца 3
Таблица 4 – Результаты расчёта для образца 4
Таблица 5 – Результаты расчёта для образца 5
Таблица 6 – Результаты расчёта для образца 6
Таблица 7 – Результаты расчёта для образца 7
Таблица 8 – Результаты расчёта для образца 8
Таблица 9 – Результаты расчёта для образца 9
Таблица 10 – Результаты расчёта для образца 10
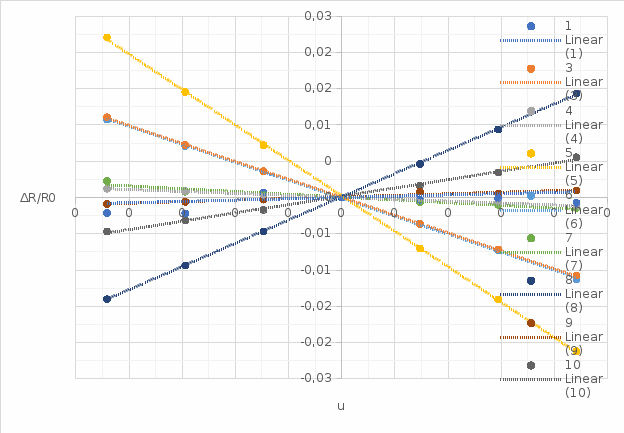   Рис 1. Экстраполированные зависимости для образцов  Рис. 3 – Экстраполированные зависимости для образцов с отмеченными экспериментальными точками 3) Таблица 11 – Тип кремния
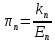 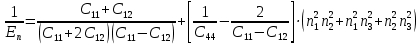 Таблица 12 – Значения модуля упругости и пьезосопротивления
4) πn = π11 + 2 ‧ (π12 + 2π44 - π11) ‧ 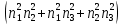 Для группы 5, 6, 7: 3,07 ‧ 109 = π11 + 2 ‧ (π12 + 2π44 - π11) ‧ 3 = 6π12 -5π11 + 12π44 = = -5π11 + 6 ‧ (π12 + 2π44) -3,22 ‧ 1011 = π11 + 2 ‧ (π12 + 2π44 - π11) ‧ 1 = 2π12 - π11 + 4π44 = = - π11 +2 ‧ (π12 + 2π44) 1,18 ‧ 1011 = π11 + 2 ‧ (π12 + 2π44 - π11) ‧ 0 = π11 Для группы 8, 9, 10: 1,3 ‧ 109 = π11 + 2 ‧ (π12 + 2π44 - π11) ‧ 0 = π11 -6,92 ‧ 1010 = π11 + 2 ‧ (π12 + 2π44 - π11) ‧ 3 = 6π12 -5π11 + 12π44 = = -5π11 + 6 ‧ (π12 + 2π44) 2,19 ‧ 1011 = π11 + 2 ‧ (π12 + 2π44 - π11) ‧ 1 = 2π12 - π11 + 4π44 = = - π11 +2 ‧ (π12 + 2π44) Таблица 13 – Коэффициенты для групп образцов
Вывод: Была проведена лабораторная работа, в результате которого были экспериментально установлены коэффициенты тензочувствительности kn , который определяет относительное изменение сопротивления при деформации и коэффициенты продольного пьезосопротивления πn , который определяет изменение удельного сопротивления под действием механических напряжений. При деформации в кристалле происходит изменение размеров зон разрешённых значений энергии, то есть изменение ширины запрещённой зоны, что приводит к изменению интенсивности обменного взаимодействия, подвижность и концентрация носителей заряда меняется также за счёт вертикального сдвига потенциального барьера между атомами кристаллической решётки. Для полупроводников n-типа, тензоэффект происходит, так как в результате анизотропной деформации экстремумы энергии становятся неэквивалентными, происходит перераспределение электронов по 6 экстремумам. Минимумы, дно которых опустились, дают большой вклад в проводимости, чем минимумы, дно которых поднимается. В направлении 111 малая тензочувстительность, так как перераспределения не произойдет. Для полупроводников p-типа в результате анизотропной деформации нарушается симметрия решетки, что приводит к снятию вырождения – потолок валентной зоны легких и тяжелых дырок смещаются в противоположных направлениях. Так как подвижности у них различны, обуславливается тензоээфект. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
