КР1. Исследование типовых радиотехнических звеньев и структурные преобразования систем радиоавтоматики
 Скачать 303 Kb. Скачать 303 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра радиотехнических систем (РТС) Контрольная работа № 1 по дисциплине «Радиоавтоматика» Тема: Исследование типовых радиотехнических звеньев и структурные преобразования систем радиоавтоматики
2022 Задание 1Определить передаточную функцию сложной системы радиоавтоматики, для чего произвести структурные преобразования.  Рисунок 1 – Структурная схема системы Таблица 1 – Вид типовых радиотехнических звеньев
Таблица 2 – Параметры типовых радиотехнических звеньев
РешениеПоследовательность преобразования структурной схемы (рис. 1) на основе правил структурных преобразований [1], представляется следующим алгоритмом: перенос узла ответвления через звено с передаточной функцией После структурных преобразований системы РА определим передаточную функцию для системы и представим в виде аналитического выражения:  Рисунок 2 – Преобразование структурной схемы исследуемой системы Далее подставим значения звеньев структурной схемы из таблицы 1 и получим: 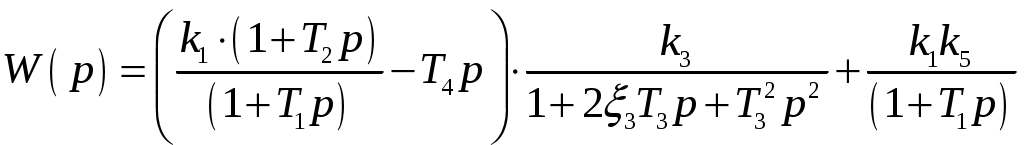 ; ;  . .Далее, согласно заданию, представим полученные выражения числителя и знаменателя в виде полиномов: максимальная степень оператора Лапласа отсюда: 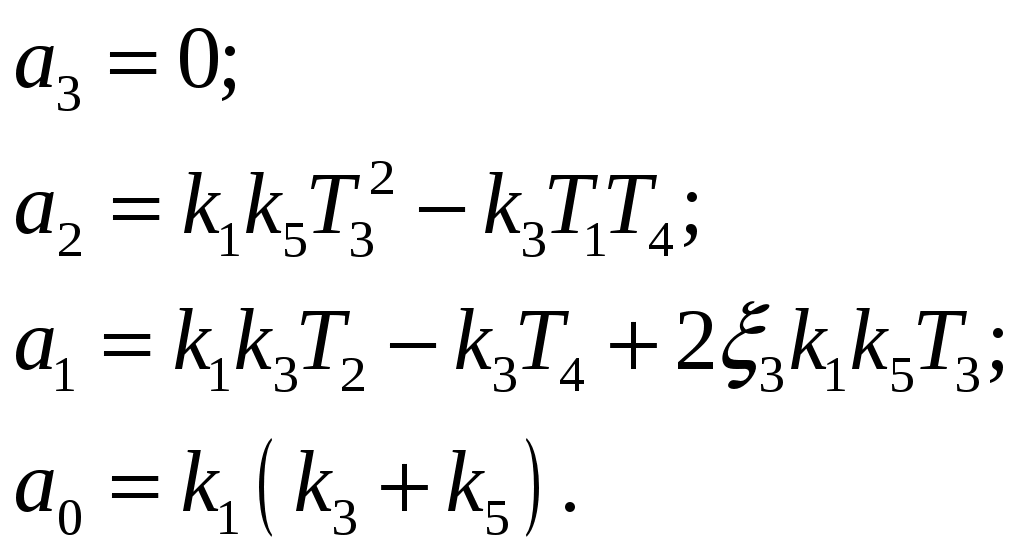 и и 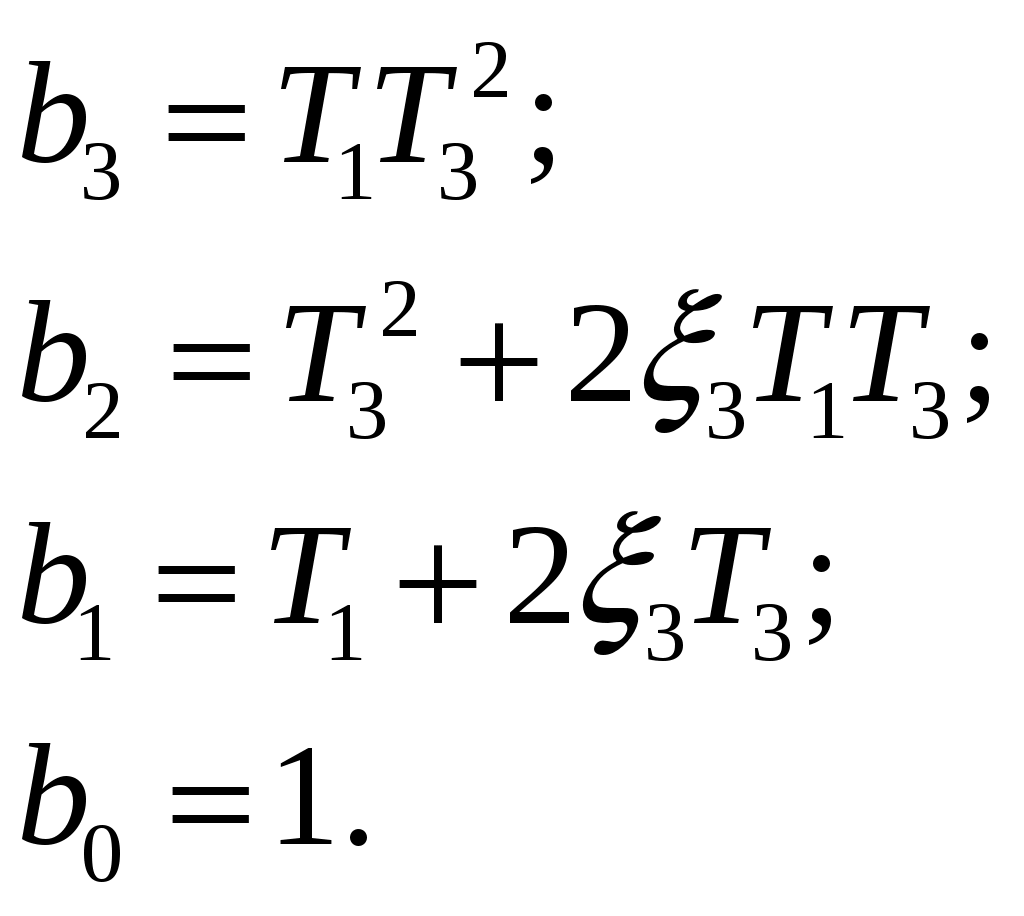 . .Затем подставим значения элементов из таблицы 2 и получим:  и  Теперь передаточная функция будет выглядеть так: полученный результат запишем в форме: В нашем случае: Задание 2Построить линеаризованную ЛАЧХ и ЛФЧХ системы радиоавтоматики. Таблица 3 – Параметры передаточной функции
РешениеЗаданная передаточная функция представляется в виде произведения типовых звеньев [1]: 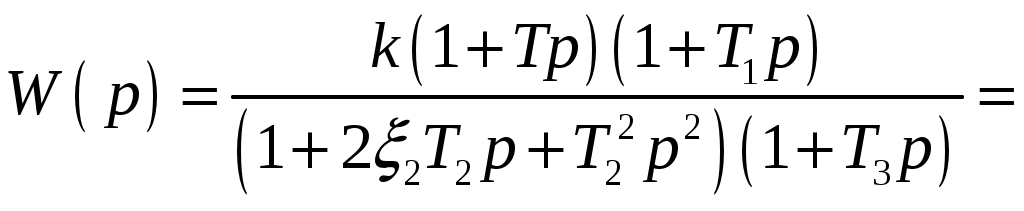  . .Коэффициент передачи системы в децибелах по формуле Таблица 4 – Коэффициенты и сопрягающие частоты
В системе присутствует два форсирующих, колебательное и апериодическое (инерционное) звенья. Построим АЧХ всех звеньев системы на одном графике [1], затем «сложим координаты» всех графиков в децибелах, чтобы получилась одна кривая (рис. 3). Аналогично поступаем при построении ФЧХ системы (рис. 4).  Рисунок 3 – АЧХ системы и типовых звеньев  Рисунок 4 – ФЧХ системы и типовых звеньев Таким образом, точки перегиба АЧХ находятся на частотах: 5; 10 рад/с, а ФЧХ: 0,5; 1; 50; 100 рад/с. Ответ на второе задание первой контрольной работы запишем в виде: АЧХ: 0 дБ/дек, 5 рад/с, –40 дБ/дек, 10 рад/с, –20 дБ/дек; ФЧХ: 0,5 рад/с, 0°; 1 рад/с, –27°; 50 рад/с, –104°; 100 рад/с, –90°. Задание 3Исследовать на устойчивость и определить запасы устойчивости, по заданному в таблице 5 параметру, замкнутой системы управления по заданной передаточной функции разомкнутой системы РА. Таблица 5 – Параметры системы и критерий устойчивости
РешениеЧислитель и знаменатель передаточной функции  Аналогично для знаменателя: 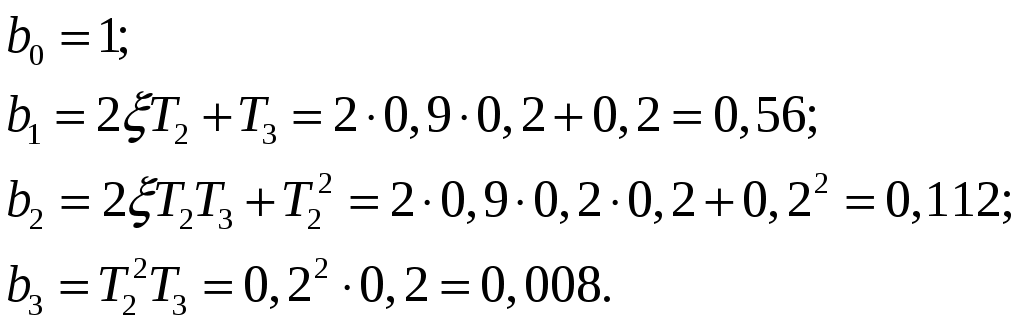 Запишем разомкнутую передаточную функцию: Для исследования устойчивости системы согласно критерию Гурвица замкнём систему, для этого воспользуемся формулой для замкнутой системы [1]:  . .и выделим характеристическое уравнение (знаменатель передаточной функции). Чтобы получить характеристическое уравнение замкнутой системы, имея передаточную функцию разомкнутой, необходимо сложить полиномы числителя и знаменателя разомкнутой передаточной функции. Таким образом, характеристическое уравнение в нашем примере будет: Подставив полученные ранее коэффициенты, получим: затем заполним «матрицу Гурвица», порядок которой совпадает с порядком системы (в нашем случае третий), где  . .Для определения устойчивости, согласно критерию Гурвица, необходимо, чтобы все элементы матрицы имели один знак и все главные миноры (определители) матрицы были положительны [1].  Все определители положительны, следовательно, система устойчива. Найдём запас устойчивости по постоянной времени первого инерционного звена, для этого в характеристическое уравнение не надо подставлять значение того параметра, по которому нужно найти запас, тогда: 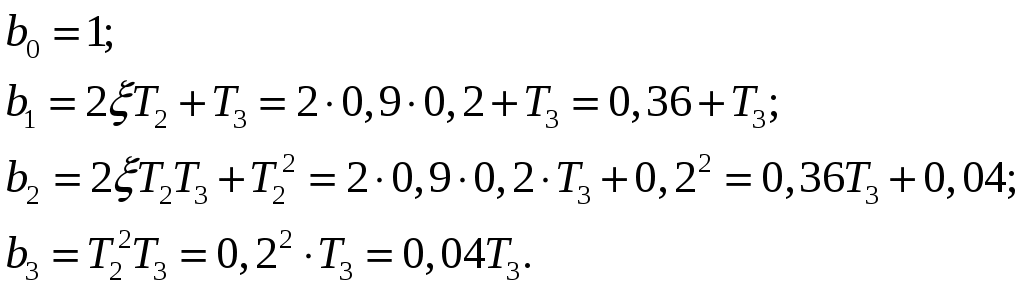 Коэффициенты Заполним «матрицу Гурвица»:  , ,тогда главные определители матрицы: 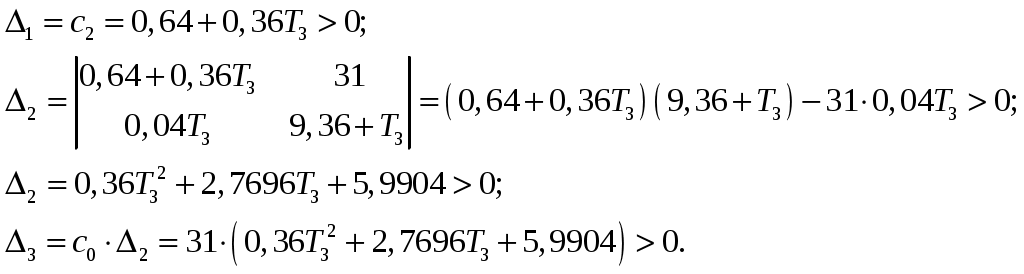 Начальные неравенства справедливы при любой положительной Ответ: система устойчива, запас устойчивости по постоянной времени бесконечен Задание 4Определить качественные показатели системы – величину перерегулирования системы (рис. 5), 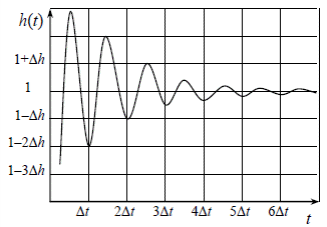 Рисунок 5 – График переходного процесса РешениеВеличину перерегулирования, характеризующую максимальное отклонение выходного сигнала от установившегося значения, можно определить по формуле: [1]: Ответ: 15 %. Список использованных источников1. Пушкарёв В. П. Радиоавтоматика : учеб. пособие / В. П. Пушкарёв, Д. Ю. Пелявин. – Томск : ФДО, ТУСУР, 2017. – 182 с. 2. Пушкарёв В. П Радиоавтоматика : учеб.-методическое пособие / В. П. Пушкарёв, Д. Ю. Пелявин. – Томск : ФДО, ТУСУР, 2017. – 100 с. |

