лабораторная. Лабораторная работа 1 Исследование типовых динамических звеньев Цель работы Изучение моделей типовых элементов в Simulink

• Название: Лабораторная работа 1 Исследование типовых динамических звеньев Цель работы Изучение моделей типовых элементов в Simulink
• Анкор: лабораторная
• Дата: 17.05.2022
• Размер: 496.23 Kb.
• Имя файла: laba_shendeleva.docx
• Тип: Лабораторная работа; #533526

Лабораторная работа № 1

Исследование типовых динамических звеньев

Цель работы

1. Изучение моделей типовых элементов в Simulink.

2. Изучение команд создания моделей типовых элементов в Matlab.

3. Изучение влияния изменения параметров передаточных функций на вид временных и частотных характеристик типовых звеньев.

Теоретическое обоснование

В системах автоматического управления используют типовые звенья:

• 
  усилительное; – интегрирующее;
  
• 
  дифференцирующее; – реальное дифференцирующее;
  
• 
  запаздывания; – форсирующее;
  
• 
  инерционно-форсирующее; – апериодическое первого порядка;
  
• 
  апериодическое второго порядка; – колебательное.
  

Усилительное звено описывается уравнением

y(t) = Ku(t), (1.1)

которому соответствует передаточная функция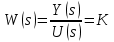

, (1.2)

где u(t), y(t) – входной и выходной сигналы, соответственно, K – коэффициент усиления, s – оператор Лапласа.

Интегрирующее звено описывается интегральным уравнением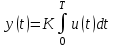

, (1.3)

которому соответствует передаточная функция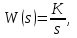

(1.4)

где U(s), Y(s) - изображение входного и выходного сигналов, соответственно.

Дифференцирующее звено описывается уравнением

(1.5)

которому соответствует передаточная функция

W(s) = T_Дs (1.6)

где Т_Д- постоянная времени дифференцирования.

Передаточная функция реального дифференцирующего звена имеет вид

(1.7)

Звено чистого запаздывания определяет выходной сигнал как

y(t) = u(t - ), (1.8)

которому соответствует передаточная функция

W(s) = e^-s, (1.9)

где - постоянная времени запаздывания.

Форсирующее звено описывается дифференциальным уравнением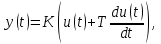

(1.10)

которому соответствует передаточная функция

W(s) = K(1 + Ts). (1.11)

Инерционно-форсирующее звено описывается уравнением

(1.12)

которому соответствует передаточная функция

(1.13)

где Т₀, Т – постоянные времени.

Апериодическое звено первого порядка описывается уравнением

(1.14)

которому соответствует передаточная функция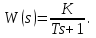

(1.15)

Апериодическое звено второго порядка описывается уравнением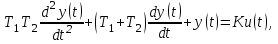

(1.16)

которому соответствует передаточная функция

(1.17)

Колебательное звено описывается дифференциальным уравнением второго порядка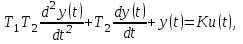

(1.18)

которому соответствует следующая передаточная функция

(1.19)

где Т₁, Т₂ – постоянные времени.

Описание работы

На рис. 1.1 представлены модели типовых динамических звеньев, реализованные с помощью библиотеки моделей Simulink.



Рис. 1.1. Моделирование временных характеристик типовых звеньев

При подаче на вход звена ступенчатой функции в окне блока Scope, подключенного к выходу звена, появится изображение его переходной функции.

На рис. 1.2 представлены результаты моделирования переходных функций типовых звеньев. При подаче на вход типового звена -функции в окне блока Scope появится изображение весовой функции. На рис. 1.3 представлены результаты моделирования весовых функций типовых звеньев.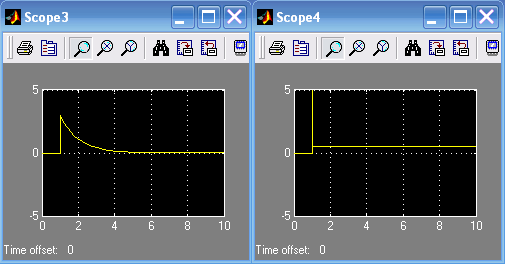



а) б) в) г)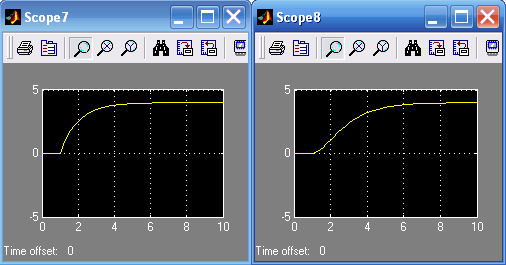



д) е) ж) з)



и) к)

Рис. 1.2. Результаты моделирования переходных функций типовых звеньев

Пакет символьной математики (Symbolic Math Toolbox) предоставляет возможности аналитического исследования временных и частотных характеристик динамических звеньев. Программа исследования поведения апериодического звена 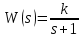в зависимости от его коэффициента усиления представлена ниже.

k=3; %Коэффициент усиления

T=2; %Постоянная времени

h1=tf([k],[T,1]); %Передаточная функция при k=3

h2=tf([2*k],[T,1]); %Передаточная функция при k=6

h3=tf([4*k],[T,1]); %Передаточная функция при k=12

figure(1) %Задание области графиков

step(h1,h2,h3),grid %Переходные функции

figure(2) %Задание области графиков

impulse(h1,h2,h3),grid %Весовые функции

figure(3) %Амплитудные и фазовые

bode(h1,h2,h3),grid %частотные характеристики

figure(4) %Задание области графиков

nyquist(h1,h2,h3),grid %Амплитудно-фазовые характеристики

syms s %Ввод символьных переменных

hp1=ilaplace(k/(s*(T*s+1))) %Обратное преобразование Лапласа

hp2=ilaplace(2*k/(s*(T*s+1))) %изображений переходных функций

hp3=ilaplace(4*k/(s*(T*s+1)))

hi1=ilaplace(k/(T*s+1)) %Обратное преобразование Лапласа

hi2=ilaplace(2*k/(T*s+1)) %изображений весовых функций

hi3=ilaplace(4*k/(T*s+1))

ltiview(h1,h2,h3) %Просмотр характеристик.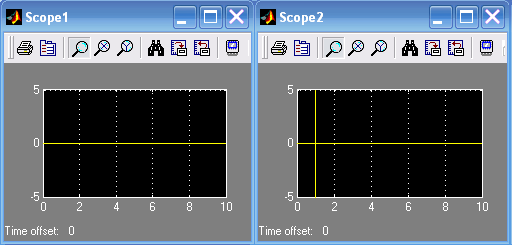



а) б) в) г)



д) е) ж) з)



и) к)

Рис. 1.3. Результаты моделирования весовых функций типовых звеньев

На рисунках 1.4 – 1.7 представлены результаты исследования апериодического звена в зависимости от коэффициента усиления k.

Программа исследования поведения апериодического звена в зависимости от его постоянной времени представлена ниже.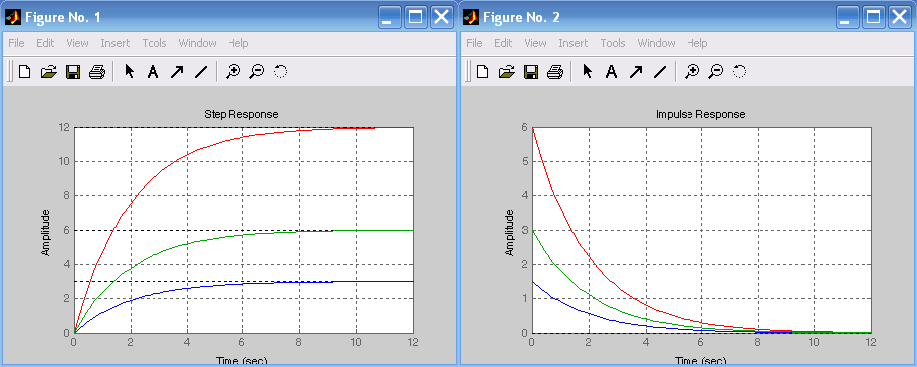



Рис.1.4. Переходные функции Рис. 1.5. Весовые функции



Рис. 1.6. АЧХ и ФЧХ Рис. 1.7. Амплитудно-фазовые характеристики

h1=tf([k],[T,1]); %Передаточная функция при Т=2

h2=tf([k],[2*T,1]); %Передаточная функция при Т=4

h3=tf([k],[4*T,1]); %Передаточная функция при Т=8

figure(1),step(h1,h2,h3),grid %Переходные функции

figure(2),impulse(h1,h2,h3),grid %Весовые функции

figure(3),bode(h1,h2,h3),grid %АЧХ и ФЧХ

figure(4),nyquist(h1,h2,h3),grid %Амплитудно-фазовые характеристики

syms s %Ввод символьных переменных

hp1=ilaplace(k/(s*(T*s+1))) %Обратное преобразование Лапласа

hp2=ilaplace(k/(s*(2*T*s+1))) %изображений переходных функций

hp3=ilaplace(k/(s*(4*T*s+1)))

hi1=ilaplace(k/(s+1)) %Обратное преобразование Лапласа

hi2=ilaplace(k/(2*s+1)) %изображений весовых функций

hi3=ilaplace(k/(4*s+1))

ltiview(h1,h2,h3) %Просмотр характеристик.

Результаты исследования представлены на рис. 1.8 – 1.11.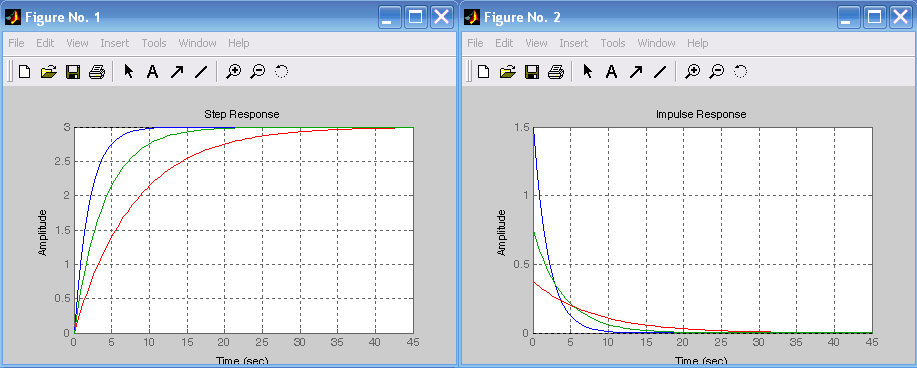



Рис.1.8. Переходные функции Рис. 1.9. Весовые функции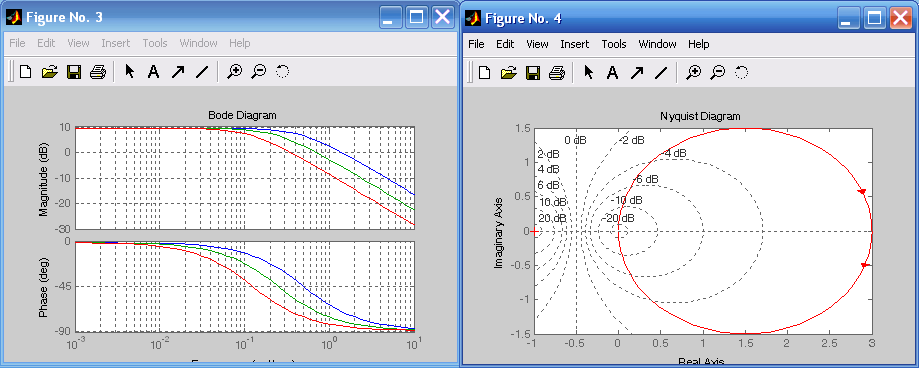



Рис. 1.10. АЧХ и ФЧХ Рис. 1.11. Амплитудно-фазовые характеристики

Определение временных и частотных характеристик инерционно-форсирующего звена 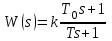в зависимости от коэффициента k:

k=3; %Коэффициент усиления

T0=0.2; %Постоянная времени Т0

T=3; %Постоянная времени Т

h1=tf(k*[T0,1],[T,1]); %Передаточная функция при k=3

h2=tf(2*k*[T0,1],[T,1]); %Передаточная функция при k=6

h3=tf(4*k*[T0,1],[T,1]); %Передаточная функция при k=12

figure(1),step(h1,h2,h3),grid %Переходные функции

figure(2),impulse(h1,h2,h3),grid %Весовые функции

figure(3),bode(h1,h2,h3),grid %АЧХ и ФЧХ

figure(4),nyquist(h1,h2,h3),grid %АФХ

syms s %Ввод символьных переменных

hp1=ilaplace(k*(T0*s+1)/(s*(T*s+1))) %Обратное преобразование

hp2=ilaplace(2*k*(T0*s+1)/(s*(T*s+1))) %Лапласа изображений

hp3=ilaplace(4*k*(T0*s+1)/(s*(T*s+1))) %переходных функций

hi1=ilaplace(k*(T0*s+1)/(T*s+1)) %Обратное преобразование

hi2=ilaplace(2*k*(T0*s+1)/(T*s+1)) %Лапласа изображений

hi3=ilaplace(4*k*(T0*s+1)/(T*s+1)) %весовых функций

ltiview(h1,h2,h3) %Просмотр характеристик.

Результаты исследования представлены на рис. 1.12 – 1.15.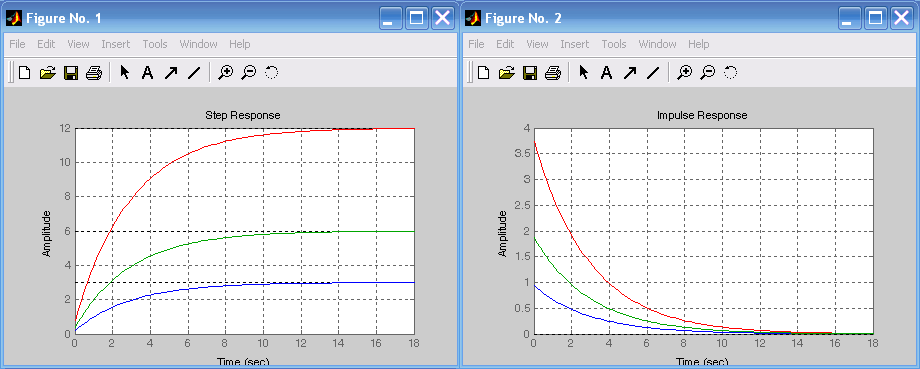



Рис.1.12. Переходные функции Рис. 1.13. Весовые функции



Рис. 1.14. АЧХ и ФЧХ Рис. 1.15. Амплитудно-фазовые характеристики

Определение характеристик инерционно-форсирующего звена в зависимости от постоянной времени представлены на рис. 1.16 – 1.19:

h1=tf(k*[T0,1],[T,1]); %Передаточная функция при T=3

h2=tf(k*[T0,1],[2*T,1]); %Передаточная функция при T=6

h3=tf(k*[T0,1],[4*T,1]); %Передаточная функция при T=12

figure(1),step(h1,h2,h3),grid %Переходные функции

figure(2),impulse(h1,h2,h3),grid %Весовые функции

figure(3),bode(h1,h2,h3),grid %АЧХ и ФЧХ

figure(4),nyquist(h1,h2,h3),grid %АФХ

syms s %Ввод символьных переменных

hp1=ilaplace(k*(T0*s+1)/(s*(T*s+1))) %Обратное преобразование

hp2=ilaplace(k*(T0*s+1)/(s*(2*T*s+1))) %Лапласа изображений

hp3=ilaplace(k*(T0*s+1)/(s*(4*T*s+1))) %переходных функций

hi1=ilaplace(k*(T0*s+1)/(T*s+1)) %Обратное преобразование

hi2=ilaplace(k*(T0*s+1)/(2*T*s+1)) %Лапласа изображений

hi3=ilaplace(k*(T0*s+1)/(4*T*s+1)) %весовых функций

ltiview(h1,h2,h3) %Просмотр характеристик



Рис.1.16. Переходные функции Рис. 1.17. Весовые функции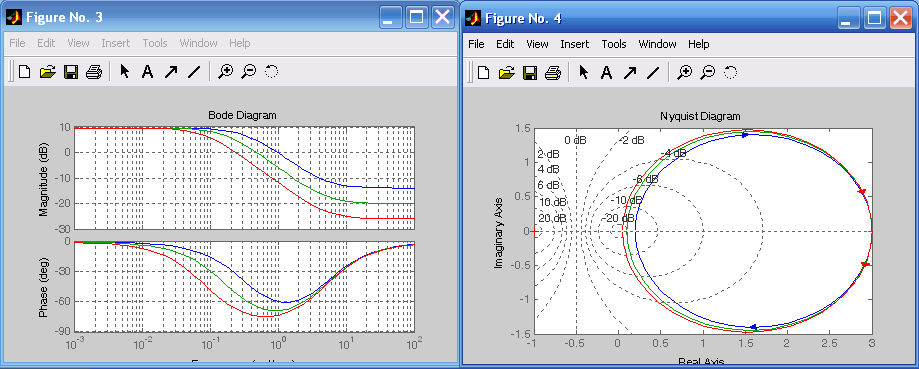



Рис. 1.18. АЧХ и ФЧХ Рис. 1.19. Амплитудно-фазовые характеристики

Определение временных и частотных характеристик колебательного звена в зависимости от коэффициента усиления k:

k=3; %Коэффициент усиления

T1=0.1; %Постоянная времени Т1

T2=0.2; %Постоянная времени Т2

h1=tf(k,[T1*T2,T2,1]); %Передаточная функция при k=3

h2=tf(2*k,[T1*T2,T2,1]); %Передаточная функция при k=6

h3=tf(4*k,[T1*T2,T2,1]); %Передаточная функция при k=12

figure(1),step(h1,h2,h3),grid %Переходные функции

figure(2),impulse(h1,h2,h3),grid %Весовые функции

figure(3),bode(h1,h2,h3),grid %АЧХ и ФЧХ

figure(4),nyquist(h1,h2,h3),grid %Амплитудно-фазовые характеристики

syms s %Ввод символьных переменных

hp1=ilaplace(k/(s*(T1*T2*s^2+T2*s+1)) %Обратное преобразование

hp2=ilaplace(k/(s*(2*T1*T2*s^2+T2*s+1)) %Лапласа изображений

hp3=ilaplace(k/(s*(4*T1*T2*s^2+T2*s+1)) %переходных функций

hi1=ilaplace(k/(T1*T2*s^2+T2*s+1)) %Обратное преобразование

hi2=ilaplace(k/(2*T1*T2*s^2+T2*s+1)) %Лапласа изображений

hi3=ilaplace(k/(4*T1*T2*s^2+T2*s+1)) %весовых функций

ltiview(h1,h2,h3) %Просмотр характеристик

Результаты исследования представлены на рис. 1.20 – 1.23.



Рис.1.20. Переходные функции Рис. 1.21. Весовые функции

Определение временных и частотных характеристик колебательного звена в зависимости от постоянной времени T₁:

k=3;T1=0.1;T2=0.2; %Коэффициент усиления, постоянные времени Т1,Т2

h1=tf(k,[T1*T2,T2,1]); %Передаточная функция при T1=0.1

h2=tf(k,[2*T1*T2,T2,1]); %Передаточная функция при T1=0.2

h3=tf(k,[4*T1*T2,T2,1]); %Передаточная функция при T1=0.4

figure(1),step(h1,h2,h3),grid %Переходные функции

figure(2),impulse(h1,h2,h3),grid %Весовые функции

figure(3),bode(h1,h2,h3),grid %АЧХ и ФЧХ

figure(4),nyquist(h1,h2,h3),grid %АФХ

syms s %Ввод символьных переменных

hp1=ilaplace(k/(s*(T1*T2*s^2+T2*s+1)) %Обратное преобразование

hp2=ilaplace(k/(s*(2*T1*T2*s^2+T2*s+1)) %Лапласа изображений

hp3=ilaplace(k/(s*(4*T1*T2*s^2+T2*s+1)) %переходных функций

hi1=ilaplace(k/(T1*T2*s^2+T2*s+1)) %Обратное преобразование

hi2=ilaplace(k/(2*T1*T2*s^2+T2*s+1)) %Лапласа изображений

hi3=ilaplace(k/(4*T1*T2*s^2+T2*s+1)) %весовых функций

ltiview(h1,h2,h3) %Просмотр характеристик

Результаты исследования представлены на рис. 1.24 – 1.27.



Рис. 1.22. АЧХ и ФЧХ Рис. 1.23. Амплитудно-фазовые характеристики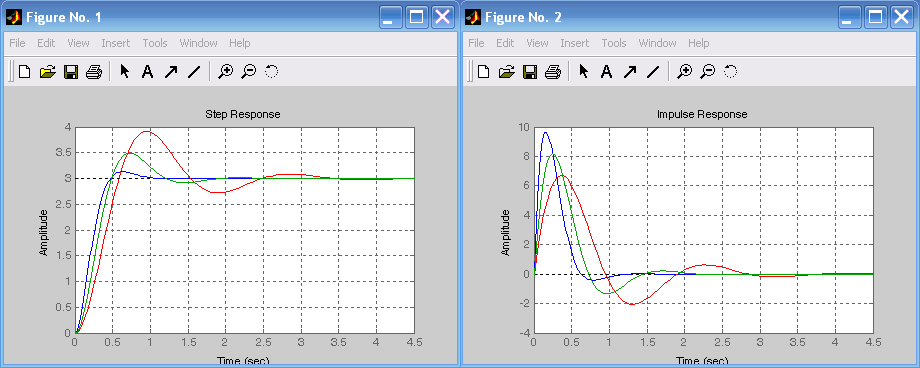



Рис.1.24. Переходные функции Рис. 1.25. Весовые функции



Рис. 1.26. Амплитудно-частотные и Рис. 1.27. Амплитудно-фазовые характеристики

фазо-частотные характеристики

В пакете МАТLAB корни характеристического уравнения знаменателя определяют следующими командами:

p=[2,1]; roots(p) %Корни апериодического звена

p=[3,1]; roots(p) %Корни инерционно-форсирующего звена

p=[0.1*0.2,0.2,1] %Корни колебательного звена

roots(p).

Задание

1. В соответствии с индивидуальным заданием в пакете Simulink построить модели типовых звеньев. Определить временные характеристики типовых звеньев при подаче ступенчатого и одиночного импульсного (-функции) входного сигнала. Моделирование одиночного импульсного сигнала осуществить с помощью последовательного соединения генератора ступенчатого сигнала и дифференцирующего звена.

2. В соответствии с индивидуальным заданием определить временные и частотные характеристики апериодического, инерционно-форсирующего и колебательного звена. Определить влияние на временные и частотные характеристики звеньев их параметров. Определить корни их характеристических уравнений.

3. 
   Выполнить обратные преобразования Лапласа переходных и весовых функций указанных звеньев.
   

Содержание отчета

1. 
   Переходные и весовые функции типовых звеньев, полученные в пакете Simulink (рис. 1.1, 1.2, 1.3).
   
2. 
   Значения корней характеристических уравнений передаточных функций апериодического, инерционно-форсирующего и колебательного звеньев.
   
3. 
   Переходные и весовые функции, амплитудно-частотные, фазо-частотные и амплитудно-фазовые характеристики апериодического звена с анализом влияния коэффициента усиления k и постоянной времени Т.
   
4. 
   Переходные и весовые функции, амплитудно-частотные, фазо-частотные и амплитудно-фазовые характеристики инерционно-форсирующего звена с анализом влияния коэффициента усиления k и постоянной времени Т.
   
5. 
   Переходные и весовые функции, амплитудно-частотные, фазо-частотные и амплитудно-фазовые характеристики колебательного звена с анализом влияния коэффициента усиления k и постоянной времени Т₁.
   

Контрольные вопросы

1. 
   Дифференциальные уравнения и передаточные функции, описывающие типовые динамические звенья.
   
2. 
   Как создать в пакете Simulink модель реального дифференцирующего звена?
   
3. 
   Как создать в пакете Simulink модель колебательного звена?
   
4. 
   Как создать в пакете Simulink модель интегрирующего звена?
   
5. 
   Как создать в пакете Simulink модель реального дифференцирующего звена?
   
6. 
   С помощью, какой команды определяют переходные функции?
   
7. 
   С помощью, какой команды определяются весовые функции?
   
8. 
   С помощью, какой команды строят ЛАХ и ЛФХ?
   
9. 
   С помощью, какой команды строят АФХ?
   
10. 
    С помощью какой команды осуществляют обратное преобразование Лапласа изображения переходной функции?
    
11. 
    С помощью какой команды осуществляют обратное преобразование Лапласа изображения весовой функции?
    
12. 
    Напишите программу, позволяющую определять корни характеристического уравнения.