 iк iк
ua
ik
  Uкk Uкk
a б
Рис.1
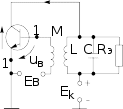
Каждая схема состоит из двух частей: 1) избирательного усилителя, содержащего активный нелинейный элемент (транзистор), входом которого яв-
ляется промежуток между точками 1 - 1, и колебательную систему (колеба- тельный контур), 2) цепи обратной связи (трансформатора), по которой ко- лебание с выхода усилителя подается обратно на его вход. Генераторы, содер- жащие избирательный усилитель и внешнюю цепь обратной связи, называются автогенераторами с внешней обратной связью. Приведем структурную схему автогенератора с внешней обратной связью, содержащую упомянутые выше части (рис.2).
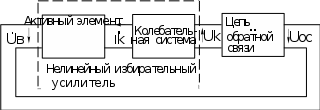
Рис.2
Здесь и далее будем использовать следующие обозначения токов и напряжений независимо от типа применяемого активного элемента (АЭ): uВ - напряжение на
входе АЭ; uа - напряжение на выходе АЭ; uк - напряжение на контуре; iв -
входной ток АЭ; iк - ток в выходной цепи АЭ.
В большинстве случаев причиной возникновения автоколебаний в гене- раторах являются флуктуации, всегда имеющие место в элементах реальной схемы. Ток, протекающий через активный элемент, всегда флуктуирует из-за наличия дробового эффекта. Другими источниками подобных, обычно весьма слабых колебаний, являются тепловое движение электронов в приборе и рези- сторах, флуктуации токораспределения в приборах и т. д. Благодаря этим явле- ниям токи и напряжения во всех элементах схемы даже при постоянстве пи- тающих напряжений быстро изменяются случайным образом. Спектр этих ко- лебаний близок по характеру к белому шуму, т.е. содержит компоненты прак- тически любых частот. Предположим, что такие флуктуации появились в на-
пряжении uв на входе активного элемента АЭ. Они вызовут колебания тока iк в выходной цепи АЭ. На выходе колебательной системы (контуре) появится на-
пряжение uк, причем, поскольку контур имеет максимальное эквивалентное со- противление ZЭ = RЭ на резонансной частоте 0, наибольшее напряжение на
нем создадут компоненты с частотами, близкими к 0. Напряжение uк через цепь обратной связи передается на вход АЭ, создавая напряжение u'в. Если ка-
кая-то компонента uв окажется в фазе с первоначальной компонентой uВ той же частоты и притом будет иметь большую амплитуду, она вызовет большее
изменение тока iк, что приведет к дальнейшему возрастанию напряжения uк и, как следствие, еще большему uв. Таков механизм самовозбуждения колебаний частоты г, близкой к 0, в процессе которого амплитуды колебаний uв, iк и uк
возрастают. Этот процесс имеет место, если на частоте г коэффициент переда-
чи напряжения по замкнутой цепи генератора больше единицы: К>1. Представ- ляя последний в виде произведения коэффициента усиления усилителя
КУ = UК/UВ и коэффициента обратной связи Ко.с = Uо.с / Uк, получим условие, необходимое для нарастания колебаний:
К = Ку Ко.с>1. (1)
Дифференциальное уравнение автогенератора. Условия самовозбуждения
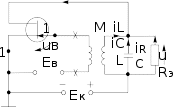
Составим дифференциальное уравнение генератора (см. рис.1), учиты- вающее только переменные составляющие токов и напряжений. Согласно пер- вому закону Кирхгофа, ток в выходной цепи
iк = iL+iC+iR . (2)
С целью упрощения расчетов используем два допущения:
а) входной ток активного элемента считаем отсутствующим (iB = 0), что дос- тигается в генераторах на полевых транзисторах подачей надлежащего смеще- ния во входную цепь, тогда
к
u L diL dt
1 iсdt ir Rэ , (3)
C
в
u M diL
dt
M u ; (4)
r
L
б) пренебрегаем влиянием выходного напряжения усилителя на ток iК, счи- тая его зависящим только от входного напряжения
iк = Ф(uв), (5)
что в большинстве случаев лишь несколько снижает точность расчетов, не вли- яя на характер получающихся зависимостей.
Выражение (5) можно рассматривать как аппроксимацию проходной ха- рактеристики активного элемента относительно рабочей точки. Производную
тока iк по времени запишем как
diк dt
diк
duв
duв dt
Suв duв , (6)
dt
где S(uв) = Ф'(uв) - крутизна характеристики (5). Заменяем токи в (2), согласно
(5) и (3):
1 u кdt C duк uк
Фu в .
L dt Rэ
о
Дифференцируя это уравнение по времени, используя (6) и (4) и обозна- чая ω2 =1/LC, получаем дифференциальное уравнение генератора:
d2uв 1
МSuв duв 2
. (7)
dt2
R
эC LC
dt
0uв 0
Это уравнение является нелинейным, поскольку коэффициент при du в/dt зави- сит от искомой переменной u в. Нелинейность уравнения является следствием наличия в схеме нелинейного элемента. Уравнение определяет все свойства рассматриваемого генератора, его решение позволяет установить и условия са- мовозбуждения, и особенности стационарны их колебаний, и характер пере- ходных процессов. При определении условий самовозбуждения колебаний нелинейное уравнение генератора (7), как уже отмечалось, может быть заменено линейным. Действительно, в этом случае нас только интересует, что будет с небольшим отклонением от состояния равновесия: станет оно затухать или нарастать. Таккак нелинейная функция S(u в), представляющая собой крутизну проходной ха-рактеристики прямой передачи, не имеет разрыва, для малых величин u в она может быть заменена значением этой функции при u в=0, т.е. крутизной S(0)=S в рабочей точке. В результате нелинейное уравнение (7) превращается в линей- ное:
d2u 1
МSdu 2
. (8)
2 0u 0
dt RэC
LCdt
Здесь напряжение u записано без индекса, поскольку уравнение справедливо и для uK, в чем легко убедиться, используя (4). Уравнение (8) можно записать как уравнение контура
d2u
du 2
, (9)
dt2
2э dt 0u 0
2 R
где э 1 1
эС
МS- эквивалентный коэффициент затухания.
LC
Его решение имеет вид
u Ae э t
sin( C t
) ,
 где А и φ - амплитуда и фаза, зависящие от начальных условий; с 2 2 -
э 1 r МSMS , (10)
2 L LC 2LC
где α = r/2L = 1/2RЭС — коэффициент затухания контура.
Уравнение (9) показывает, что генератор эквивалентен колебательному контуру, коэффициент затухания которого уменьшен на величину MS/2LC, за- висящую от взаимоиндукции М, т.е. от обратной связи. Полученный результат означает, что переменное напряжение на входе активного элемента, благодаря
наличию обратной связи, создает ток iк, доставляющий в колебательную систе- му энергию, компенсирующую потери в ней. Необходимая же энергия пере-
менного тока iк получается благодаря тому, что переменное напряжение uв управляет расходом энергии источника постоянного тока, имеющимся в вы- ходной цепи, т.е. благодаря преобразованию энергии постоянного тока в энер- гию переменного тока.
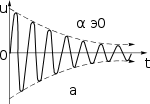
Если обратная связь невелика (αЭ > 0 или MS/C < r), вносимая энергия лишь частично компенсирует расходуемую в колебательной системе, поэтому возникшее колебание затухает, хотя и медленнее, чем в отсутствие обратной связи. При достаточно сильной обратной связи коэффициент αЭ оказывается отрицательным (вносимая энергия больше расходуемой) и колебания нара-
стают. Рассмотрим зависимость характера колебаний от αэ (рис. 3).
 uα э0 uα э0
0t
б
Рис.3
или
Условия самовозбуждения генератора можно записать как
αэ <0 (11)
M > MKP = L/SRЭ = rC/S. (12)
В рамках допущений, принятых при выводе уравнения генератора, коэф- фициент обратной связи Ко.с = М/L, а коэффициент усиления усилителя
Кy = SRэ. Поэтому условие самовозбуждения (12) идентично условию (1).
Обратная связь, способствующая самовозбуждению колебаний, называ- ется положительной. В рассмотренном случае она соответствует M>0. Если знак М изменить на обратный, для чего достаточно поменять местами точки подключения одной из обмоток трансформатора, то затухание контура возрас- тет и самовозбуждение станет невозможным. Обратная связь, затрудняющая самовозбуждение, т.е. увеличивающая устойчивость состояния равновесия, на- зывается отрицательной. Следовательно, для создания автогенераторов необхо- димо использование положительной обратной связи.
Стационарный режим автогенератора
Точных аналитических методов решения нелинейных дифференциаль- ных уравнений (за редким исключением) не существует. В связи с этим было разработано большое количество разнообразных методов приближенного ана- лиза нелинейных цепей. Каждый метод обладает определенными пре- имуществами при решении круга задач. Наиболее распространенными метода- ми являются: метод линеаризации; квазилинейный метод (метод гармонической линеаризации); метод медленно меняющихся амплитуд; метод фазовой плоско- сти; метод малого параметра; метод математического моделирования.
Наибольшее распространение для инженерных расчетов стационарных режимов автогенераторов получил квазилинейный метод, основанный на ис- следовании соотношений между первыми гармониками токов и напряжений и замене нелинейною элемента эквивалентным линейным, характеризуемым средним по первой гармонике параметром. После такой замены нелинейная цепь описывается линейными уравнениями и может исследоваться методами линейной теории (например методом комплексных амплитуд). Квазилинейный метод применим для систем, колебания в которых близки к гармоническим.
Рассмотрим схему автогенератора (см. рис.1) с контуром в выходной цепи усилителя, активным элементом которого могут быть биполярный или полевой транзистор. Благодаря значительной добротности (обычно порядка 50 – 200) колебательные контуры генераторов обладают большой изби- рательностью. Поэтому даже тогда, когда выходной ток усилителя сильно от- личается от синусоидального из-за нелинейности АЭ, напряжения на контуре
uк и на входе АЭ uв оказываются почти синусоидальными, лишь незначительно
отличающимися от их первых гармоник uк1 , uв1. Анализируемый генератор со- стоит из двух частей: нелинейной (АЭ) и линейной (контура и катушки связи). Запишем соотношения между комплексными амплитудами первых гармоник токов и напряжений. Нелинейный элемент будем характеризовать средней кру- тизной, определяемой отношением комплексных амплитуд тока İК1 в выходной цепи АЭ к амплитуде напряжения возбуждения ÚB1 на входе АЭ:
S& сp I&К1/UВ1 . (13)
Вследствие нелинейности АЭ S& ср
зависит от амплитуды
U& B1 . Пренебрегая
влиянием напряжения ÚК1 на ток İК1, получим из (13)
I&К1 S& срUВ1 . (14)
Если первая гармоника тока iK1 совпадает по фазе с первой гармоникой
напряжения возбуждения uB1 , средняя крутизна оказывается действительной. Однако на практике при работе на достаточно высоких частотах в результате конечного времени прохождения носителей через прибор ток iK1 отстает по фа- зе от uB1. Поэтому в общем случае среднюю крутизну (13) следует считать ком- плексной.
Для линейной части схемы (см. рис. 1) при iB1=0 имеем ÚK1= İ К1ZЭ и
Uв1 K& о.с.Uк1 K& о.с.ZэI&к1 причем комплексный коэффициент обратной связи
(15)
К& О.С. .=ÚB1 /ÚК1=M/L=KО.С.
оказывается действительным. Произведение КО.СZЭ, характеризующее линей- ную часть схемы, называют управляющим сопротивлением:
ZУ = КО.СZЭ. (16)
Подставляя (14) в (15), получим комплексное уравнение генератора:
S& срК& о.с.Zэ
1.
(17)
Оно имеет очевидный физический смысл: в стационарном режиме ком плексный коэффициент передачи по замкнутому контуру ге- нератора равен единице. Если воспользоваться (16), придем к иной форме комплексного уравнения генератора:
S& СР ZУ 1.
(18)
Представляя каждую из комплексных величин в показательной форме
S& ср
Sсреis ,
K& о.с. Kо.с.eiк ,
Zэ Zэeiк , (19)
можем записать уравнение (17) в виде
SсрKо.с.Zэei(s к z )
1. (20)
Уравнение (20) имеет место, если одновременно выполняются два условия:
s к z
0,2π,…, 2πn (21)
SсрKо.с.Zэ 1
(22)
Соотношения (21), (22) являются важнейшими в теории автогенераторов, определяющими параметры стационарного режима. Выражение (21), называе- мое условием баланса фаз, означает, что в стационарном режиме сумма всех
фазовых сдвигов по замкнутому контуру генератора равна нулю или целому числу 2π. Поскольку каждый из сдвигов фаз, входящих в это выражение, зави- сит от частоты по-разному, в большинстве генераторов существует лишь одна частота ω0, на которой выполняется условие баланса фаз, т.е. на которой возможно генерирование колеб аний. Таким образом, из условия балан- са фаз определяется частота генерируемых колебаний.
Выражение (22), называемое условием баланса амплитуд, говорит о том, что в стационарном режиме коэффициент передачи по замкнутому контуру ге-
нератора равен единице. В этом условии две величины (Ко.с и Zэ) от амплитуды
колебаний не зависят, а одна (Scp) зависит от UB1. Следовательно, условие ба- ланса амплитуд выполняется лишь при определенной амплитуде UB1. Для опре- деления амплитуды стационарных колебаний удобно (22) переписать в виде
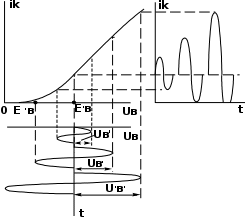
Sср(UB1) = 1/Ко.с.Zэ. (23)
Рассмотрим (рис. 4) построенные зависимость Scp(UB1), называемую характеристикой средней крутизны, и прямую обратной связи, проведенную на
уровне 1/Ко.сZэ. Точка пересечения этих зависимостей определяет стационар- ную амплитуду колебаний ƯB1, для которой выполняется условие баланса ам- плитуд. Если частота генерируемых колебаний равна резонансной частоте кон- тура, то Zэ=Rэ и условие баланса амплитуд
Sср(UB1) = 1/Ко.сRэ. (24)
Scp
0U'В1UВ1
 Рис.4 Рис.4
Стационарный режим будет устойчивым, если большая амплитуда UВ1 станет затухать, т.е. если при UВ1>U'В1 величина αЭ окажется положительной. Для этого требуется, чтобы
∂SCP/∂UВ1<0. (25)
Таким образом, стационарный режим автоколебаний я вля - ется устойчивым, если производ ная средней крутизны по ампли- туде напряжения отрицательна.
Режимы возбуждения колебаний в автогенераторе
В квазилинейном методе для определения амплитуды стационарных ко- лебаний применяется также подход, основанный на использовании колебатель- ных характеристик.
Колебательной характеристикой называется зависимость амплитуды IK1 первой гармоники выходного тока нелинейного элемента от амплитуды UB входного гармонического напряжения:
IK1 = Ф1(UB). (26)
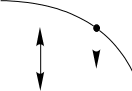
 Колебательная характеристика определяется по динамической вольт- амперной характеристике прибора (рис. 5): при выбранном смещении ЕВ для различных амплитуд входного напряжения (U'''B>U''B>U'B) строим графики тока iK и рассчитываем амплитуды их первых гармоник IK1. Для смещения Е'B, соот- ветствующего участку с постоянной крутизной S, при небольших амплитудах UB IK1=SUB. По мере увеличения UB напряжение все больше заходит на участки меньшей крутизны, в результате чего рост амплитуды IK1 замедляется (рис. 6,а). Колебательная характеристика определяется по динамической вольт- амперной характеристике прибора (рис. 5): при выбранном смещении ЕВ для различных амплитуд входного напряжения (U'''B>U''B>U'B) строим графики тока iK и рассчитываем амплитуды их первых гармоник IK1. Для смещения Е'B, соот- ветствующего участку с постоянной крутизной S, при небольших амплитудах UB IK1=SUB. По мере увеличения UB напряжение все больше заходит на участки меньшей крутизны, в результате чего рост амплитуды IK1 замедляется (рис. 6,а).
Рис.5
Если смещение Е''B соответствует нижнему загибу характеристики iK(uВ), то с увеличением UB сначала IK1 растет быстрее UB, а затем приблизительно пропорционально UB, что приводит к колебательной характеристике II. При больших амплитудах UB амплитуды IK1 всегда уменьшаются из-за влияния на- пряжения на нагрузке.
При любой амплитуде UB средняя крутизна
Scp = tgα, (27)
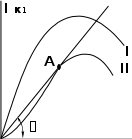
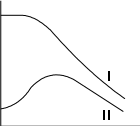
где α - угол наклона линии, соединяющей точку колебательной характеристики с началом координат. Рассмотрим характеристики средней крутизны Scp(UB), соответствующие колебательным (I и II) (рис. 6, б). При малых UB Scp опреде- ляется крутизной S в рабочей точке Sср(0)=S.
Режим работы генератора с характеристиками I называется мягким, а с
характеристиками II - жестким. Отметим, что при характеристике II наиболь-
шее значение Scp соответствует точке А (см. рис. 6,а), в которой касательная к колебательной характеристике проходит через начало координат.
  Scp Scp
0aUв 0
бUв
Рис.6
Следует отметить, что при анализе работы генератора в мяг- ком режиме вольт- амперная характеристика его нелинейного элемента должна быть аппроксимирована полиномом не ниже третьей степени, а в жестком – не ниже пя той степени.
Рассмотрим особенности каждого режима.
Мягкий режим. Помимо колебательной характеристики IK1 = Ф(UВ1) на схеме (рис. 7, а) построено семейство характеристик обратной связи, опреде- ляющих зависимость UВ1 от IK1 через линейные элементы генератора. Эти ха- рактеристики будут соответствовать выражению (15), если в последнем заме- нить комплексные амплитуды на модули: UB1 = Kо.сZэIк1. Решая это уравнение
относительно IK1 и учитывая, что Kо.с = M/L, получаем уравнение характери- стик обратной связи:
IK1 = (L/MZэ)UB1. (28)
IK1M1M2M3M4 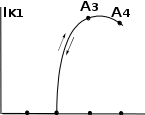 A3A4 A3A4
|
 Скачать 315 Kb.
Скачать 315 Kb.
 Колебательная характеристика определяется по динамической вольт- амперной характеристике прибора (рис. 5): при выбранном смещении ЕВ для различных амплитуд входного напряжения (U'''B>U''B>U'B) строим графики тока iK и рассчитываем амплитуды их первых гармоник IK1. Для смещения Е'B, соот- ветствующего участку с постоянной крутизной S, при небольших амплитудах UB IK1=SUB. По мере увеличения UB напряжение все больше заходит на участки меньшей крутизны, в результате чего рост амплитуды IK1 замедляется (рис. 6,а).
Колебательная характеристика определяется по динамической вольт- амперной характеристике прибора (рис. 5): при выбранном смещении ЕВ для различных амплитуд входного напряжения (U'''B>U''B>U'B) строим графики тока iK и рассчитываем амплитуды их первых гармоник IK1. Для смещения Е'B, соот- ветствующего участку с постоянной крутизной S, при небольших амплитудах UB IK1=SUB. По мере увеличения UB напряжение все больше заходит на участки меньшей крутизны, в результате чего рост амплитуды IK1 замедляется (рис. 6,а).
 Scp
Scp
 A3A4
A3A4






