Лаба 2(3). Исследование устойчивости линейных систем автоматического управления Группа эм83 Бригада 6 Состав бригады
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Новосибирский государственный технический университет Кафедра электропривода и автоматизации промышленных установок ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ Дисциплина: "Теория автоматического управления" Работа № 2 Наименование: Исследование устойчивости линейных систем автоматического управления Группа ЭМ-83 Бригада №6 Состав бригады: Работа защищена:_________________________________ Преподаватель: 2020 г. Цель работы: Используя метод структурного моделирования, исследовать заданную систему автоматического управления на устойчивость. Установить влияние параметров системы на её устойчивость и определить их граничные (крити-ческие) значения. Общие сведения: Одной из важнейших динамических характеристик системы автоматического управления является её устойчивость. Под устойчивостью понимается свойство системы возвращаться к исход-ному состоянию равновесия или заданному закону движения после прекра-щения (снятия) воздействия, отклонившего систему от предписанного ей движения. Неустойчивая система не возвращается к предписанному режиму работы, а непрерывно от него удаляется или совершает около него возрастающие колебания. Очевидно, что такая система не может выполнять возложенные на неё функции – она оказывается неработоспособной. Помимо устойчивого (неустойчивого) режима в линейной САУ возможны ещё два режима движения: граница устойчивости и нейтральная устойчивость. Граница устойчивости – это переход от устойчивости к неустойчивости или наоборот. В этом режиме в системе возникают незатухающие колебания относительно заданного движения. Такая система также является неработоспособной. Нейтральная устойчивость – это режим, когда отклонения от предписанного движения стремятся к постоянной величине, зависящей от начальных условий (в устойчивой системе отклонения стремятся к нулю). Нейтральную устойчивость следует рассматривать, как особую устойчивость системы управления. Формулировка критерия Гурвица: Для устойчивости САУ необходимо и достаточно, чтобы при 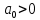 все диагональные миноры определителя Гурвица были положительными. все диагональные миноры определителя Гурвица были положительными.Определитель Гурвица составляется из коэффициентов характеристического уравнения заданной системы по определенным правилам.
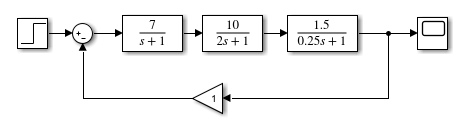  Рисунок 1– Структурная схема САУ Программа лабораторной работы: Для заданной САУ снять график переходной функции и по её виду определить устойчивость системы. Исследовать влияние коэффициента передачи (k=105) на устойчивость системы: определить граничное значение коэффициента передачи (kгр) и найти области устойчивости (неустойчивости). Снять графики переходных функций устойчивого и неустойчивого режимов работы и границы устойчивости. Выставить на модели заданное значение коэффициента передачи и исследовать влияние постоянной времени на устойчивость системы: определить граничные значения постоянной времени и найти области устойчивости (неустойчивости). Снять графики переходных функций устойчивого и неустойчивого режимов работы и границ устойчивости. Ход работы: Для заданной САУ снять график переходной функции и по её виду определить устойчивость системы. 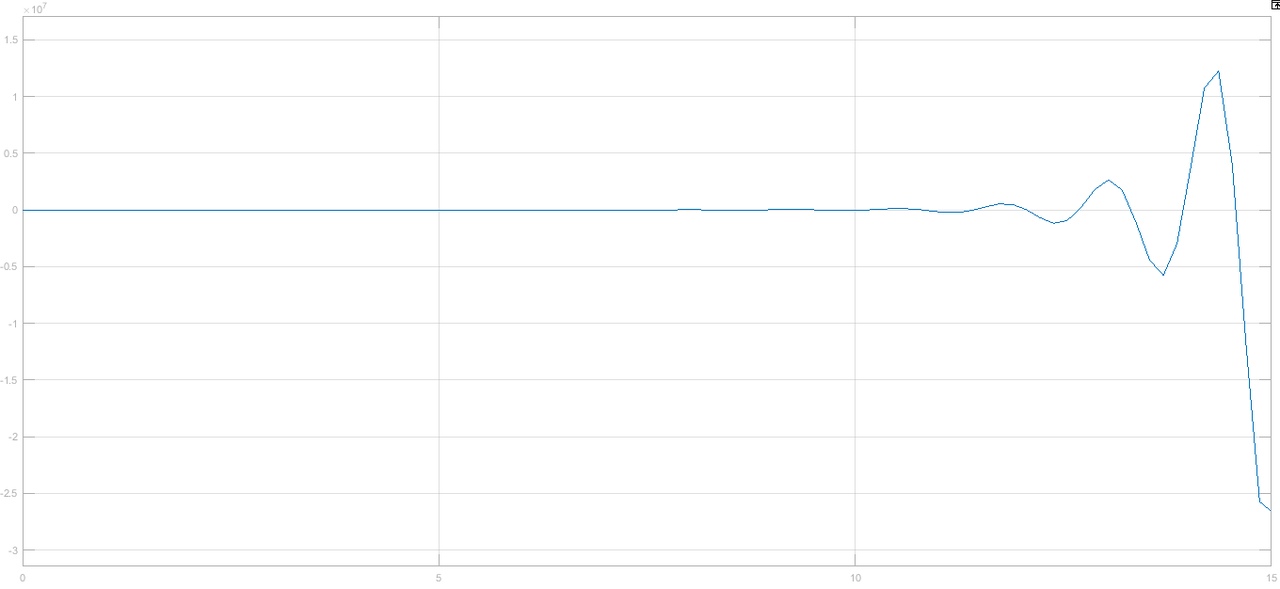  Рисунок 2– График переходной функции для заданного САУ Вывод: Методом цифрового моделирования мы выяснили, что САУ неустойчивая, т.к. на графике переходной функции изображен колебательный расходящийся переходный процесс. Определим устойчивость и влияние параметров САУ на ее устойчивость по критерию Гурвица: 1) Передаточная функция САУ (в замкнутом состоянии): 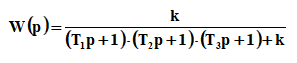 (1) 2) Численные значение параметров: 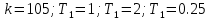 3 (2) 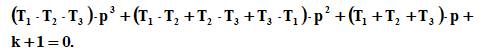 Раскроем скобки, приведем подобные и запишем характеристическое уравнение в принятой форме записи: Раскроем скобки, приведем подобные и запишем характеристическое уравнение в принятой форме записи:(3) Обозначим коэффициенты уравнения и найдем их значения: 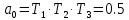 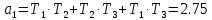 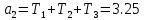 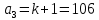 (4)   Определитель Гурвица: Определитель Гурвица: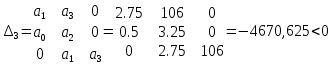 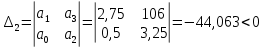 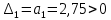 Условия устойчивости: 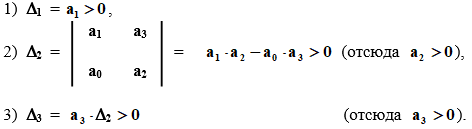 Окончательно условие устойчивости получим в следующем виде: 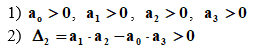 Вывод: В нашем случае условия не выполняются, поэтому система неустойчивая. Определим влияние коэффициента передачи на устойчивость системы. Прежде всего необходимо найти граничные значения интересующих параметров системы (возьмем, к примеру, коэффициент передачи 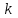 и постоянную времени и постоянную времени 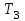 ). ).Найдем граничное значение коэффициента передачи 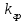 . .Для этого запишем условие нахождения заданной САУ на границе устойчивости ( 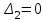 ) через параметры САУ и возьмем в качестве неизвестного параметра коэффициент передачи системы ) через параметры САУ и возьмем в качестве неизвестного параметра коэффициент передачи системы 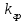 : :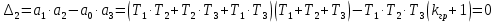 (7) (7) (8) Из (7) найдем 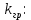 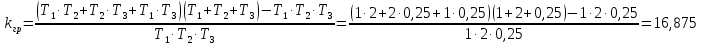  Рисунок 3– График переходной функции на границе устойчивости ( 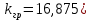 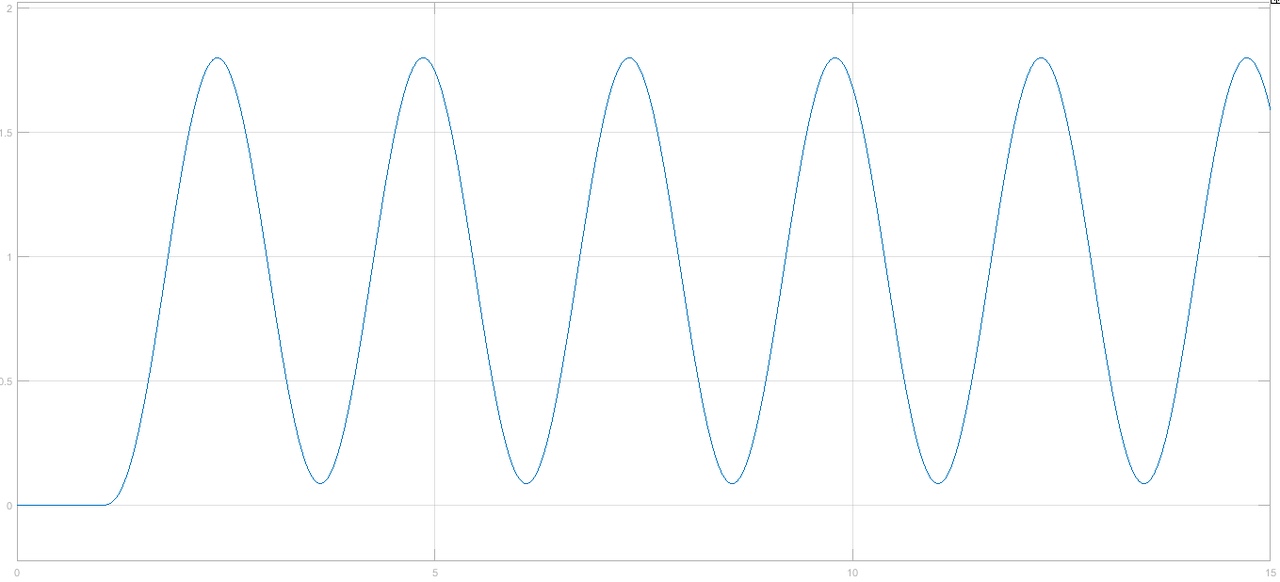 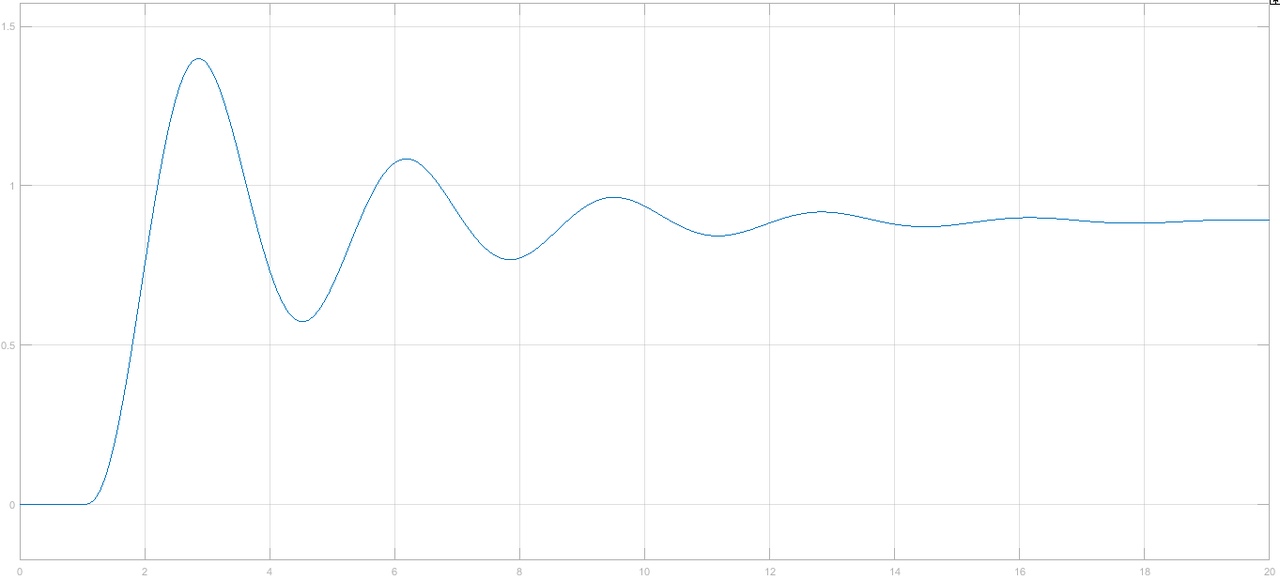 Вывод: при данном значении Вывод: при данном значении 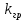 на графике видны автоколебания, а значит САУ находится на границе устойчивости и расчеты на графике видны автоколебания, а значит САУ находится на границе устойчивости и расчеты 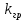 выполнены правильно. выполнены правильно.      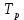 Рисунок 4– График переходной функции устойчивого режима работы ( 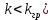 Вывод: при значении меньше 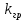 график переходной функции принимает колебательный сходящийся вид, а значит САУ устойчива. график переходной функции принимает колебательный сходящийся вид, а значит САУ устойчива.График имеет 3 колебания; 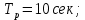 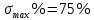 Области устойчивости (неустойчивости):          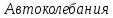 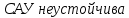 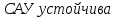 0 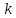  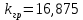  Рисунок 5– Области устойчивости (неустойчивости) в зависимости от коэффициента передачи Вывод: В данном пункте мы нашли граничный коэффициент устойчивости, который равен 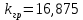 , если мы берем значение k< , если мы берем значение k<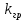 , то САУ устойчива, а если k> , то САУ устойчива, а если k> 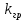 , то САУ неустойчива (график переходной функции для этого условия изображен на Рисунке 2). , то САУ неустойчива (график переходной функции для этого условия изображен на Рисунке 2). Исследуем влияние постоянной времени на устойчивость системы. Найдем граничное значение постоянной по времени 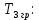 Возьмём в качестве неизвестного параметр 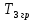 и запишем условие границы устойчивости: и запишем условие границы устойчивости: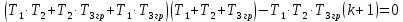 (9) (9) Подставим исходные данные из Таблицы 1 в (9): 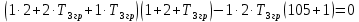 (10) (10)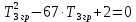 (11) (11)В 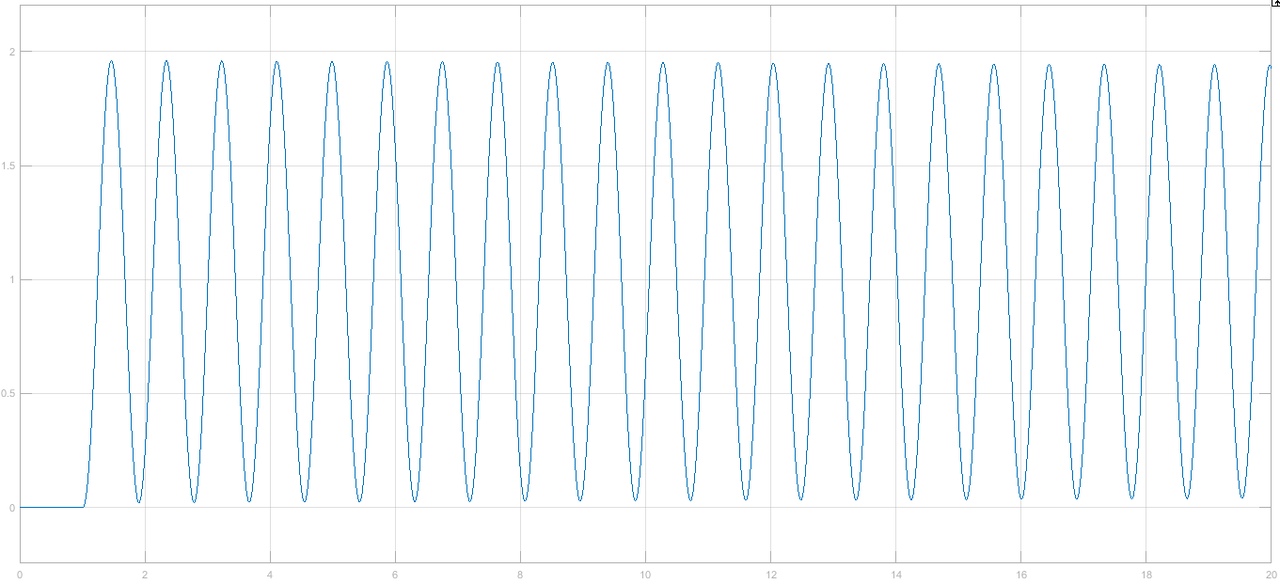 ычислив уравнение (11) мы получим два корня ычислив уравнение (11) мы получим два корня 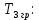 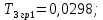 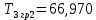  Рисунок 6– График переходной функции на границе устойчивости ( 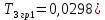 Вывод: при данном значении 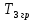 на графике видны автоколебания, а значит САУ находится на границе устойчивости и расчеты на графике видны автоколебания, а значит САУ находится на границе устойчивости и расчеты 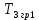 выполнены правильно. выполнены правильно. Рисунок 6– График переходной функции на границе устойчивости ( 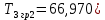 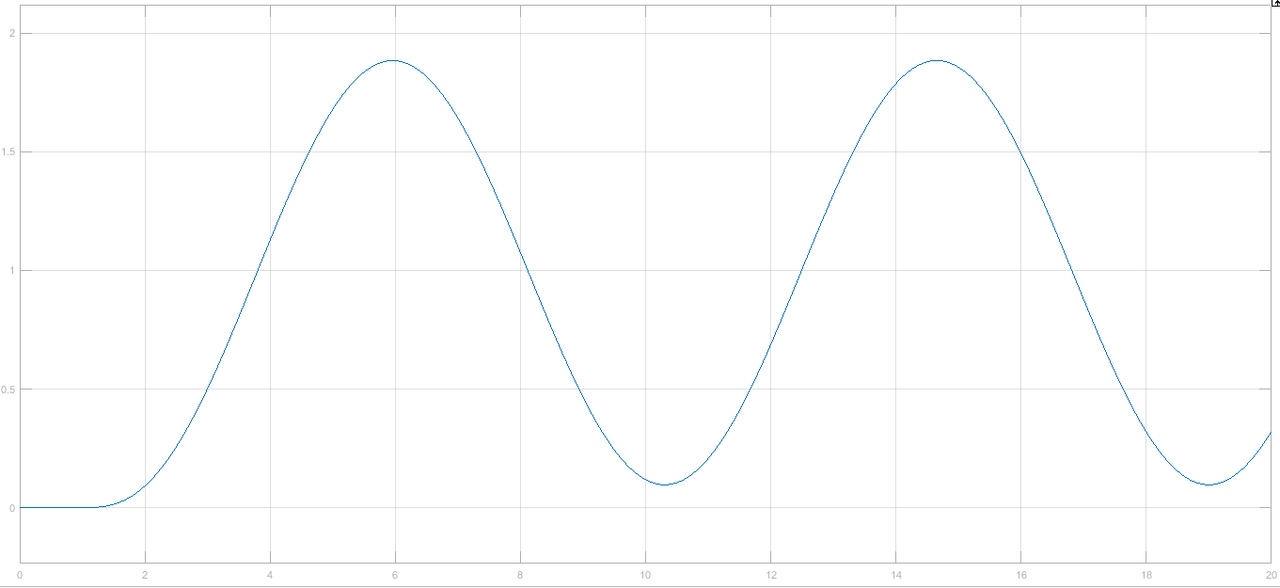 Вывод: при данном значении 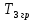 на графике видны автоколебания, а значит САУ находится на границе устойчивости и расчеты на графике видны автоколебания, а значит САУ находится на границе устойчивости и расчеты 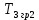 выполнены правильно. выполнены правильно.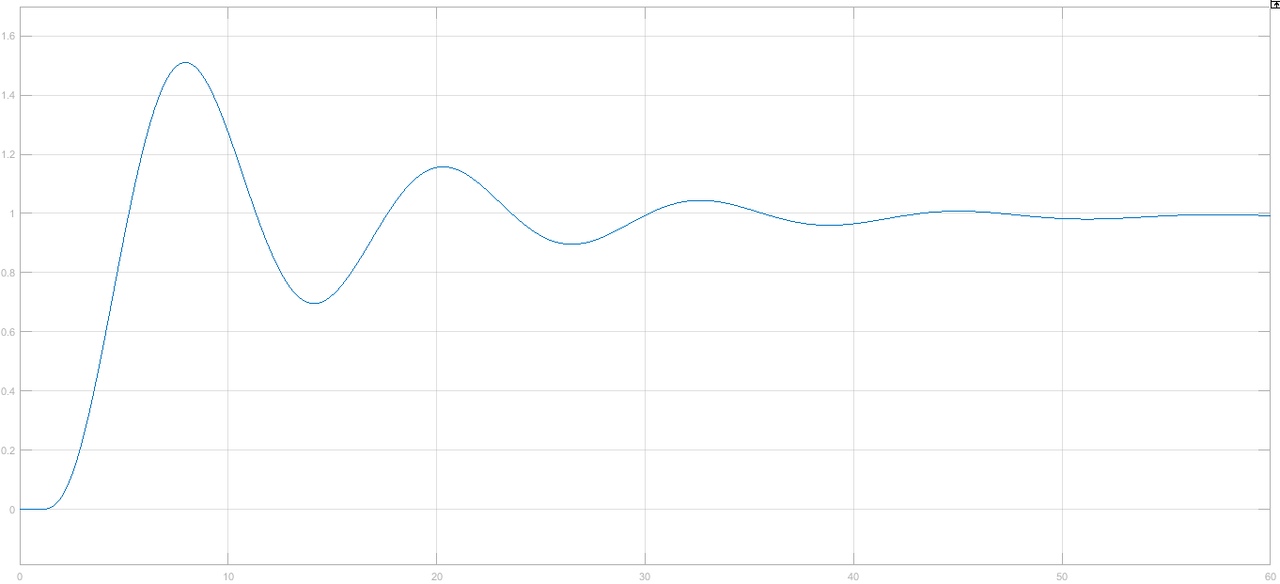     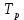  Рисунок 7– График переходной функции устойчивого режима работы ( 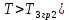 Вывод: при значении T > 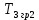 , в данном случае T=150, график переходной функции принимает колебательный сходящийся вид, а значит САУ устойчива. , в данном случае T=150, график переходной функции принимает колебательный сходящийся вид, а значит САУ устойчива.График имеет 3 колебания; 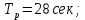 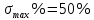     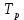 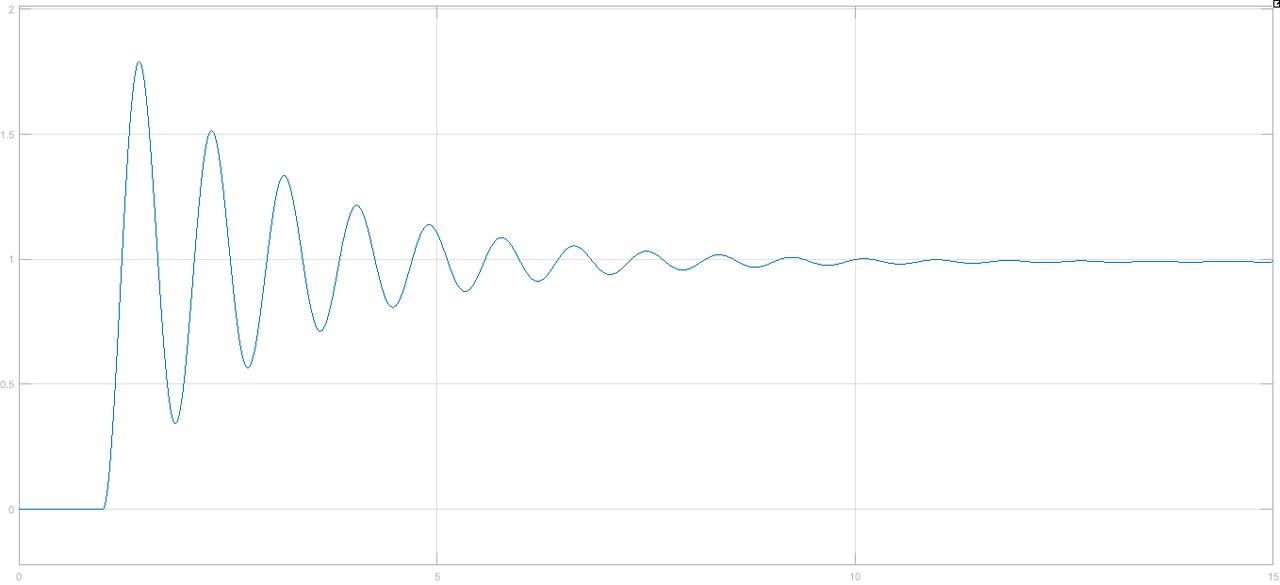  Рисунок 8– График переходной функции устойчивого режима работы ( 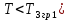 Вывод: при значении T < 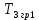 , в данном случае T=0,01, график переходной функции принимает колебательный сходящийся вид, а значит САУ устойчива. , в данном случае T=0,01, график переходной функции принимает колебательный сходящийся вид, а значит САУ устойчива.График имеет 6 колебания; 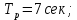 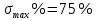 Области устойчивости (неустойчивости):                  Рисунок 9– Области устойчивости (неустойчивости) в зависимости от постоянной по времени Вывод: В данном пункте мы нашли граничные значения постоянной по времени, 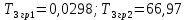 , если мы берем значения T< , если мы берем значения T<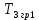 и T> и T>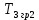 , то САУ устойчива, а если , то САУ устойчива, а если 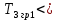 T T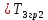 , то САУ неустойчива (график переходной функции для этого условия изображен на Рисунке 2). , то САУ неустойчива (график переходной функции для этого условия изображен на Рисунке 2). Автоколебания Автоколебания T 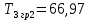 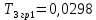    0 | ||||||||||||||||||||
