Туртан султан 13 вариант. Туртан Султан 13 вариант. Расчёт системы автоматического регулирования двигателя постоянного тока
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
Министерство образования и науки Республики Казахстан НАО «Карагандинский индустриальный университет» Кафедра «Энергетика» Курсовой проект По дисциплине: «Системы управления электроприводом» Тема: Расчёт системы автоматического регулирования двигателя постоянного тока Выполнила: студент гр. ЭЭ-17к Туртан С.Д. Проверил:ст.пр. Сиверская Т.И. Темиртау2020 г  СОДЕРЖАНИЕ СОДЕРЖАНИЕВведение. 4 1. Расчет динамических параметров контура тока 8 1.1 Расчет параметров преобразовательного трансформатор 8 для двигателя постоянного тока 2ПФ200LГУХЛЧ 1.2 Составляем принципиальную электрическую схему силовой 10 части тиристорного электропривода 2. Расчет параметров регулятора тока 15 2.1.Согласно принципу компенсации составляем 15 ередаточную функцию «ПИ» регулятора тока 2.2 .Составляем структурную схему системы регулирования тока 16 3 Расчет динамических параметров контура регулирования скорости 19 3.1 Структурная схема замкнутого контура тока оптимизированного 19 по модульному оптимуму 4. Расчет параметров регулятора скорости 21 4.1 Расчет параметров пропорционального регулятора скорости 21 Список литературы 25 ВВЕДЕНИЕ При неизменном токе возбуждения характер переходных процессов в двигателе постоянного тока зависит от двух динамических параметров якорной цепи: электромагнитной постоянной времени контура тока ТЭ и электромеханической постоянной времени привода ТЭМ. Электромагнитная постоянная времени ТЭ при ступенчатом приложении напряжения к якорной цепи невозбужденного двигателя определяет время нарастания тока якоря и численно равна:  Электромеханическая постоянная времени ТЭМ при ступенчатом приложении напряжения к якорной цепи определяет время нарастания скорости вращения двигателя до практически установленного значения и численно равна  , где , где  Наиболее распространенным принципом построения регулятора является компенсация основных инерционностей объекта управления. Этот термин следует понимать в широком смысле, а именно это регулятор компенсирующий действие звеньев с большими постоянными времени не только инерционного характера, но и интегральных, форсирующих. Принцип компенсации можно сформулировать следующим образом: каждому звену объекта управления с большой постоянной времени должно соответствовать звено с обратной передаточной функцией в составе регулятора. Поэтому для построения передаточной функции регулятора необходимо знание динамических параметров объекта управления.  1. Динамические параметры якорной цепи двигателя постоянного тока. 1. Динамические параметры якорной цепи двигателя постоянного тока.Ниже приведены уравнения, характеризующие динамические свойства электродвигателя, которые соответствуют общеизвестным структурным схемам электродвигателя постоянного тока при изменении напряжения на якоре: 1.1уравнения электрического равновесия в якорной цепи двигателя  или или 1.2 уравнение ЭДС двигателя  1.3 уравнение момента двигателя 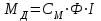  1.4 уравнение механического равновесия 1.4 уравнение механического равновесия , ,где Еr – ЭДС генератора, В; 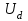 – ЭДС тиристорного преобразователя, В; – ЭДС тиристорного преобразователя, В;Е – ЭДС двигателя, В; МСТ – момент статистической нагрузки, Н∙м; МД – момент двигателя, Н∙м; 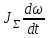 – динамический момент, Н∙м; – динамический момент, Н∙м;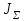 – момент инерции двигателя с механизмом приведенный к валу двигателя, кг∙м2; – момент инерции двигателя с механизмом приведенный к валу двигателя, кг∙м2; – угловая скорость, рад/с; СЕ, СМ – конструктивные постоянные двигателя;  ; ;  Примечание: при измерении скорости в рад/с   . При определении индуктивности двигателя LЯД, на практике наибольшее распространение получила формула Уманского-Линвила. . При определении индуктивности двигателя LЯД, на практике наибольшее распространение получила формула Уманского-Линвила. , Гн , Гнгде С – коэффициент, равный 0,15 0,25 для компенсированных машин; С –0,6 для некомпенсированных машин; р – число пар полюсов; nн – номинальная частота вращения двигателя; Uн – номинальное напряжение двигателя; Iн – номинальный ток двигателя. 2. Расчет параметров якорной цепи. Значения LЭ и RЭ для тиристорных электроприводов определяются следующим образом (при мостовой схеме преобразования): LЭ = LЯД + Lа + Lс.р, RЭ = RЯД + Rа + Rф+Rс.р + Rш где Lа – индуктивность анодной цепи преобразователя; Lс.р – индуктивность сглаживающего реактора; Rа –активное сопротивление анодной цепи преобразователя, Ом; Rф – эквивалентное сопротивление преобразователя, учитывающее коммутацию тока в вентилях; Rш = 0,1RЯД.– активное сопротивление шин или кабельной линии.  – активное сопротивление фазы трансформатора, приведенное ко вторичной обмотке. – активное сопротивление фазы трансформатора, приведенное ко вторичной обмотке.Рк.з – потери короткого замыкания; I2ф.н – номинальный фазный ток вторичной обмотки трансформатора.  – индуктивное сопротивление трансформатора. – индуктивное сопротивление трансформатора.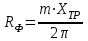 – при мостовой схеме m=6; – при мостовой схеме m=6;Rа=2Rтр + 2Rо.р , La=2Lтр +2Lо.р Rо.р – активное сопротивление ограничивающего реактора;  – индуктивность трансформатора. – индуктивность трансформатора.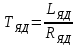 – электромагнитная постоянная времени двигателя; – электромагнитная постоянная времени двигателя; – электромагнитная постоянная времени контура тока. – электромагнитная постоянная времени контура тока. – электромеханическая постоянная времени привода. – электромеханическая постоянная времени привода.3. Основные соотношения, используемые в расчетах. I2ф=I2л – при соединении вторичной обмотки в «звезду».   – при соединении вторичной обмотки в «треугольник». – при соединении вторичной обмотки в «треугольник». – при мостовой схеме выпрямителя. – при мостовой схеме выпрямителя. Rа=2Rтр – активное сопротивление обмоток трансформатора при мостовой схеме выпрямления и вторичной обмотки, собранной в «звезду». Rа=2Rтр – активное сопротивление обмоток трансформатора при мостовой схеме выпрямления и вторичной обмотки, собранной в «звезду». – активное сопротивление обмоток трансформатора – активное сопротивление обмоток трансформатора при мостовой схеме выпрямления и вторичной обмотки, собранной в «треугольник». La=2Lтр – при схеме «звезда».  –при схеме «треугольник». –при схеме «треугольник». 1.РАСЧЕТ ДИНАМИЧЕСКИХ ПАРАМЕТРОВ КОНТУРА ТОКА. 1.РАСЧЕТ ДИНАМИЧЕСКИХ ПАРАМЕТРОВ КОНТУРА ТОКА.1.1 Расчет параметров преобразовательного трансформатора для двигателя постоянного тока 2ПФ200LГУХЛЧ. Р = 14 кВт Uн = 220 В nн = 1000 об/мин nmax = 3300 об/мин ном = 82 % Rя = 0,136 Ом, при t = 15 0С RДП = 0,084 Ом, при t = 15 0С Rвоз = 46/13- Ом, при t = 15 0С LН = 4,4∙10-3 Гн J1= 0,23 кг·м2 Jмех= 0,5 кг·м2 Номинальное значение тока двигателя определяем по формуле: Iн=  А АПроизводим расчет и выбор тиристорного преобразователя с условием: Udн ≥ Uн; Idн ≥ Iн. По справочнику [1] выбираем электропривод серии КТЭ с номинальными данными UН = 220 В, IН = 100 А. Определяем максимальное напряжение преобразователя Udо с учетом номинального напряжения двигателя Uн: Udо = Uн ∙ К1 ∙ К2∙ К3 = 220 ∙ 1,15 ∙ 1,05 ∙ 1,05 = 278,933 В, Где К1 ∙=1,15 – коэффициент, учитывающий снижение напряжения сети; К2 ∙=1,05 – коэффициент, учитывающий ограничение угла управления αmin; К3 ∙=1,05 – коэффициент, учитывающий явление коммутации в ТП. Необходимое фазное напряжение обмотки трансформатора: 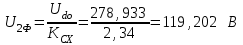 Линейное напряжение обмотки трансформатора:  Значение тока вторичной обмотки трансформатора:   Требуемая мощность трансформатора:  По справочнику [1] выбираем трансформатор ТС3П 25/0,7УХЛ4. SТ = 29,1 кВА U1Л = 380 В U2Л = 205 В I2 = 82 А Рх.х. = 210 Вт Рк.з. = 1100 Вт uк % = 5,5 % соединение звезда-треугольник – 11 1.2 Составляем принципиальную электрическую схему силовой части тиристорного электропривода.  Рисунок. 1 Принципиальная схема системы ТП-Д 1.3 Расчет статистических и динамических параметров якорной цепи электропривода Активное сопротивление двигателя Rя.д. = т(Rя + Rд.п) = 1,24 (0,136 + 0,084) = 0,2728 Ом Где т =1+0,004 = 1 + 0,004∙60 = 1,24 = 60С – превышение температуры двигателя над температурой, окружающей среды. Активное сопротивление фазы трансформатора, приведенное ко вторичной обмотке. 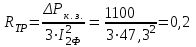 Ом Ом Где Где 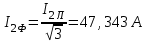 Индуктивное сопротивление фазы трансформатора, приведенное ко вторичной обмотке 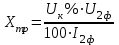   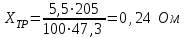 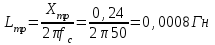 Сопротивление, обусловленное явлением коммутации 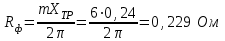 Сопротивление кабельной продукции соединяющий двигатель с преобразовательным устройством принимаем равным 0,1∙Rя.д. Rш = 0,1Rя.д. = 0,1 0,2728=0,002728 Ом Так как схема преобразования мостовая, а схема соединения вторичной обмотки трансформатора «треугольник», то значения сопротивления и индуктивности трансформатора Ra = Rтр = 0,2 Ом.  Гн ГнВ случае схемы соединения вторичной обмотки трансформатора в «звезду» полученные значения сопротивления и индуктивности трансформатора необходимо увеличивать в 2 раза. Ra = 2Rтр 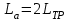 Индуктивность сглаживающего дросселя, включаемого последовательно в цепь якоря двигателя, выбирается из условий обеспечения непрерывности тока двигателя во всем диапазоне нагрузок (от Idмин до Idн) и ограничения пульсаций тока id до 3 – 5% Idн.  , Гн, , Гн,где IA=Idмин – минимальная величина тока нагрузки, равная Iх.х двигателя; m – число фаз выпрямителя; w – угловая частота, w=2πf1 (для частоты сети f1=50 Гц w=314); Uп – действующее значение переменной составляющей выпрямленного напряжения (для трехфазной мостовой схемы Uп/Ud0=0,246). Требуемая индуктивность сглаживающего дросселя:  В данном случае реактор не требуется Находим полное сопротивление контура тока  RЭ = Rя.д. + Rа+ Rф + Rш + Rо.р RЭ = Rя.д. + Rа+ Rф + Rш + Rо.р RЭ = 0,2728 + 0,4 + 0,229 + 0,02728 + 0 = 0,929 Ом. Индуктивность контура тока Lэ = Lя.д.+ Lа + Lо.р=0,0044 + 0,00016 + 0 = 0,006 Гн Электромагнитная постоянная времени контура тока  Электромагнитная постоянная времени двигателя.  Производим расчет «малых некомпенсируемых» постоянных времени контура тока. Постоянные времени СИФУ и датчика тока согласно [6] принимаем соответственно Ту=1∙10–3 с – постоянная времени СИФУ. Тд.т. =1∙10–3 с – постоянная времени датчика тока.  – среднестатистическое запаздывание преобразователя [7]. – среднестатистическое запаздывание преобразователя [7].Определяем «малую некомпенсируемую» постоянную времени по формуле [7]. 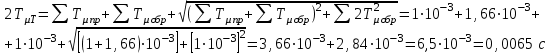 где ∑Тμпр=Ту+Тв ∑Тμобр=Тдт ∑Тμпр-постоянная времени прямого канала регулирования ∑Тμобр-постоянная времени обратного канала регулирования. ТμТ=0,00325 с Определяем передаточные коэффициенты контура регулирования тока. Передаточный коэффициент измерительного шунта якорной цепи. Выбираем Iш=200А 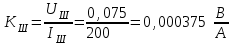 Коэффициент датчика тока определяем исходя из максимальных величин якорного тока и напряжения в канале управления. Для системы регулирования преобразовательного устройства серии КТЭ максимальное напряжение управления составляет 9÷10В, тогда коэффициент обратной связи по току составит  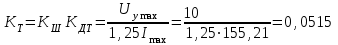 где 1,25 - коэффициент настройки токовой защиты  2,0 – коэффициент, учитывающий максимальный ток двигателя обеспечивающий технологический процесс, при разгоне или торможении. 2,0 – коэффициент, учитывающий максимальный ток двигателя обеспечивающий технологический процесс, при разгоне или торможении.Определяем коэффициент датчика тока  Принимаем фиксированное значение коэффициента КДТ=150 (из ряда: 50, 100, 150, 200) Находим действительное значение КТ  Максимальное напряжение обратной связи Uос при I=Imax 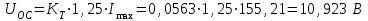 Коэффициент усиления тиристорного преобразователя при косинусоидальной форме опорного напряжения  где Uy900-максимальное напряжение управления необходимое для изменения угла управления на 900. В случае пилообразного опорного напряжения 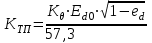 где Кθ=90/10=9град/В - крутизна рабочего участка, т.е. передаточный коэффициент СИФУ  В преобразователях серии КТЭ – линейное опорное напряжение В преобразователях серии КТЭ – линейное опорное напряжение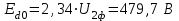 57,3-переводной коэффициент Кθ в радианную меру еd=Еd/Ed0=0-относительное значение ЭДС преобразователя при еd=0, значение КТП будет максимальным 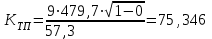 На основании результатов расчета составляем передаточную функцию тиристорного преобразователя и двигателя постоянного тока по току.    2.РАСЧЕТ ПАРАМЕТРОВ РЕГУЛЯТОРА ТОКА 2.РАСЧЕТ ПАРАМЕТРОВ РЕГУЛЯТОРА ТОКА2.1.Согласно принципу компенсации составляем передаточную функцию «ПИ» регулятора тока  Согласно принципа технического оптимума выбираем коэффициент усиления регулятора тока по формуле 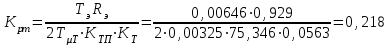 Частота среза разомкнутого контура тока 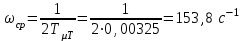 Постоянная интегрирования регулятора тока  Принимаем масштабный коэффициент равным единице, т.е. RЗТ/RT=1 Задаемся значением емкости Сос=0,5∙10-6 Ф, тогда  Определяем значение сопротивления RЗТ из выражения  Расчетные значения RЗТ, Roc приводят к ближайшим стандартным значениям, но чтобы отклонения не превышали ±5%. Составляем схему «ПИ» регулятора тока     Рисунок 2. Принципиальная схема «ПИ» регулятора тока  2.2 Составляем структурную схему системы регулирования тока 2.2 Составляем структурную схему системы регулирования тока Рисунок.3. Структурная схема системы регулирования тока Составляем результирующую передаточную разомкнутого контура тока оптимизированного по модульному оптимуму.  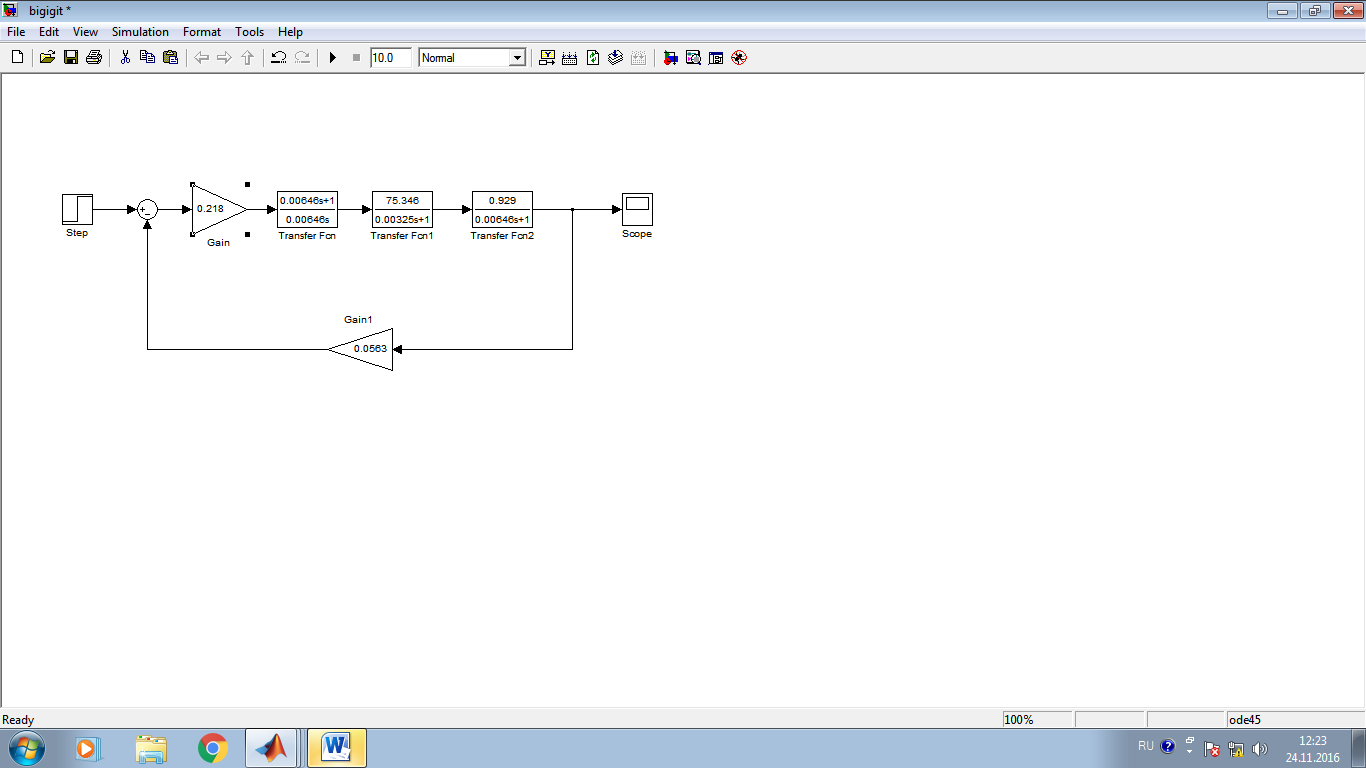 Рисунок 4а Структурная схема системы регулирования тока, оптимизированной по М.О. 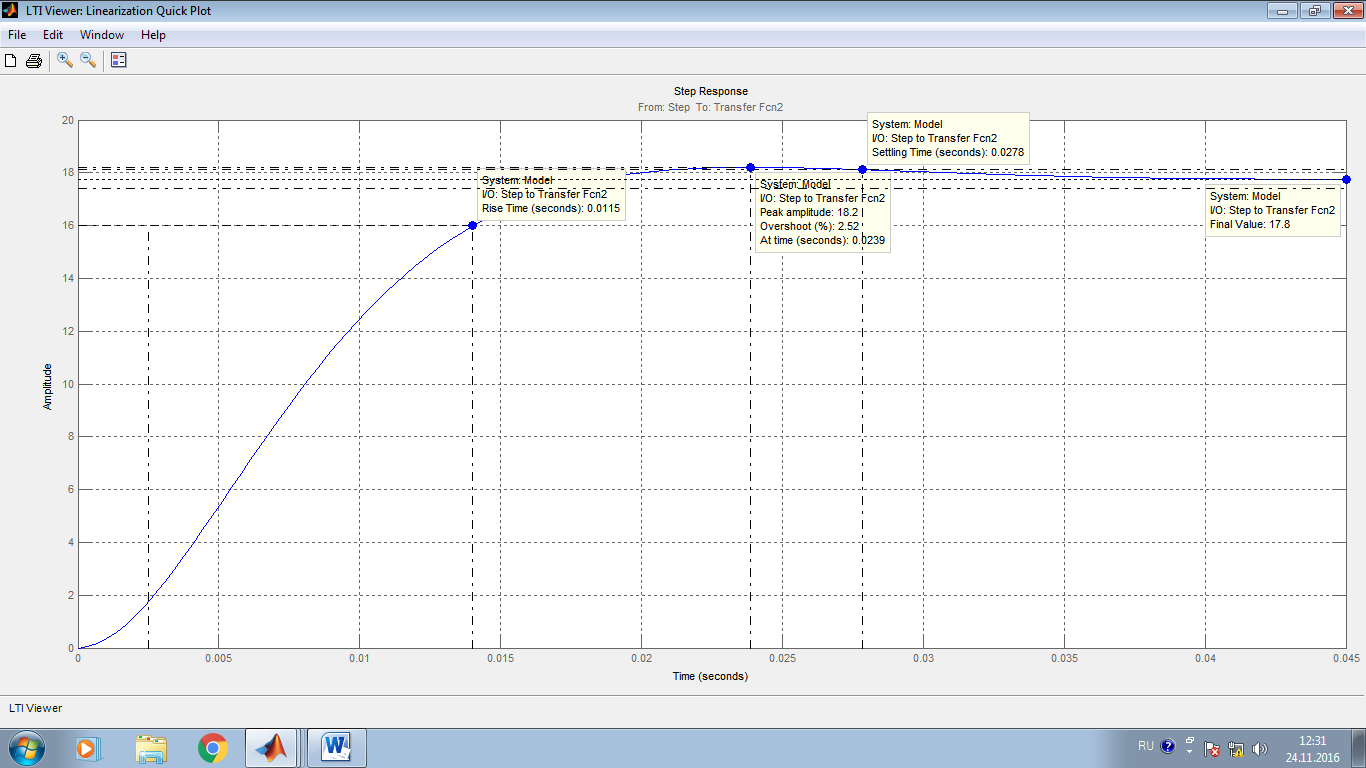 Рисунок 4б Кривая переходной функции   Рисунок 5 ЛАЧХ, ЛФЧХ разомкнутого контура тока 4. Пользуясь прикладным программным комплексом «Matlab» производим построение кривой переходной функции ЛАЧХ, ЛФЧХ системы регулирования тока. 5. По результатам исследования производим анализ качества регулирования. 1. частота среза ωср=  2. запас устойчивости по фазе ∆φ0=20,40 3. перерегулирование δ%=2,303% 4. время достижения первого согласования tс=0,0115с 5. время достижения первого максимума tμ=0,0278 с 6. время переходного процесса tр=0,0239 с   3 РАСЧЕТ ДИНАМИЧЕСКИХ ПАРАМЕТРОВ КОНТУРА РЕГУЛИРОВАНИЯ СКОРОСТИ. 3 РАСЧЕТ ДИНАМИЧЕСКИХ ПАРАМЕТРОВ КОНТУРА РЕГУЛИРОВАНИЯ СКОРОСТИ.3.1 Структурная схема замкнутого контура тока оптимизированного по модульному оптимуму  . Рисунок 6. Структурная схема контура тока. после соответствующего преобразования получаем результирующую передаточную функцию замкнутого контура тока. 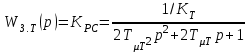 Результирующая передаточная функция представляет собой систему второго порядка. Важнейшей характеристикой такой системы является коэффициент демпфирования  где α-коэффициент при р2 β- коэффициент при р таким образом, коэффициент демпфирования при оптимизации по модульному оптимуму равен 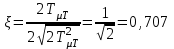 В дальнейшем в передаточной функции Wзт(р) замкнутого контура тока член 2ТμТ2р2 с достаточной для практических расчетов точностью можно опустить, если последовательно с ним включено интегрирующее или инерционное звено с постоянной времени Т>>ТμТ. В  нашем случае последовательно будет включено интегрирующее звено с электромеханической постоянной времени Тэм, которое намного больше ТμТ. нашем случае последовательно будет включено интегрирующее звено с электромеханической постоянной времени Тэм, которое намного больше ТμТ.Таким образом, передаточная функция замкнутого контура тока будет иметь вид  В дальнейшем примем обозначение 2ТμТ=ТТ  4 .РАСЧЕТ ПАРАМЕТРОВ РЕГУЛЯТОРА СКОРОСТИ 4 .РАСЧЕТ ПАРАМЕТРОВ РЕГУЛЯТОРА СКОРОСТИ4.1 Расчет параметров пропорционального регулятора скорости. Для однократной интегрирующей системы передаточная функция регулятора скорости по МО должна иметь вид  где Тμс–некомпенсируемая малая постоянная времени контура скорости Тμс =Тт +Тф.о.с. где Тт-постоянная времени замкнутого контура тока Тф.о.с.-постоянная времени фильтра в цепи обратной скорости В нашем случае для простоты расчета принимаем Тф.о.с.=0,001с. По предыдущему примеру расчета контура тока Тт=2Т  =2·0,00325=0,0065 =2·0,00325=0,0065тогда Тμc =Тт +Тф.о.с.=0,0065+0,001=0,0075 с Кт=0,0563; RЭ=0,929 Ом; Rя.д.=0,2728 Ом по условию оптимизации по техническому оптимуму Ткс=2Тμс=2·0,075=0,015 с Находим значения СeФ и СМФ 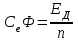 , ,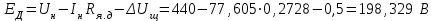   ; ;  ; ;   ; ;  Электромеханическая постоянная времени привода 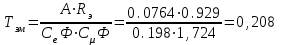   Кр.с= 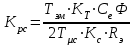 Находим значение К  Принимаем U3max=10В 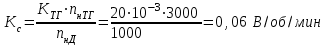 - коэффициент обратной связи по скорости - коэффициент обратной связи по скорости    . Рисунок 8 Структурная схема контура скорости  Рисунок. 9а Переходной процесс разомкнутого контура скорости   Рисунок. 9б ЛАЧХ, ЛФЧХ разомкнутого контура скорости По результатам исследования производим анализ качества регулирования. 1. Частота среза ωср= 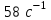 2. Запас устойчивости по фазе ∆φ0=19,1 3. Перерегулирование δ%=77,25% 4. время достижения первого согласования tс=0,274 с 5. время достижения первого максимума tμ=3,8 с 6. время переходного процесса tр=0,0873 с   СПИСОК ЛИТЕРАТУРЫ СПИСОК ЛИТЕРАТУРЫПод. ред. В. М. Перельмутера «Комплектные тиристорные электроприводы». Справочник. М., Энергоатомиздат, 1988. 318с. Анучин, А.С. Системы управления электроприводов / А.С. Анучин. - Вологда: Инфра-Инженерия, 2015. - 373 c. Москаленко, В.В. Системы автоматизированного управления электропривода / В.В. Москаленко. - Вологда: Инфра-Инженерия, 2016. - 208 c. Аксенов, М.И. Моделирование электропривода: Учебное пособие / М.И. Аксенов. - М.: Инфра-М, 2014. - 104 c. Якуничева, О.Н. Проектирование электропривода промышленных механизмов: Учеб-ное пособие / О.Н. Якуничева, А.П. Прокофьева. - СПб.: Лань, 2014. - 448 c Терехов В.М. Системы управления электроприводов : Учеб. / Терехов В.М. - 3-е изд.,стер. - М.: Академия, 2008. - 304 с. Шеховцов В.П. Электрическое и электромеханическое оборудование : Учеб. / Шеховцов В.П. - 2-е изд. - М.: Форум, 2009. - 416 с. Вольдек А.И., Попов В.В. Электрические машины. Введение в электромеханику. Машины постоянного тока трансформаторы : Учеб. для вузов / Вольдек А.И.,Попов В.В. - СПб: Питер, 2008. - 320 с. |
