ЛР3. ЛР3 (Д23В) (с мет.ук.). Исследование влияния сопротивления на вынужденные колебания механической системы с одной степенью свободы
 Скачать 288.84 Kb. Скачать 288.84 Kb.
|
|
Задание Д23В. Исследование влияния сопротивления на вынужденные колебания механической системы с одной степенью свободы (дополнение к заданию Д23 «Исследование свободных колебаний механической системы с одной степенью свободы» в книге А.А.Яблонский «Сборник заданий для курсовых работ по теоретической механике», М., 1985). Используя решение задания Д23, найти решение этой же задачи при условии, что на тело 1 дополнительно действует сила сопротивления, характеризуемая коэффициентом затухания n, а на блок (диск), вращающийся вокруг неподвижной оси, действует возмущающая сила G,направленная вниз и приложенная на расстоянии x от оси тела 2 (рис.1) (варианты 1,2,4,8-13,16-20,25,27-30), или тела 3 (варианты 3,15,21), или тела 4 (варианты 5,6,7,14), или тела 5 (варианты 24,26). Выполняется: G=20 Н, x=X0sinpt м, X0=0,05 м, p=kN/6, где N-номер варианта, k-частота собственных колебаний. Получить уравнения колебаний и в любом графическом пакете построить три кривые колебаний на одном графике для случаев: 1) n=0,5k; 2) n=k; 3) n=1,5k. Для всех случаев принять нулевые начальные условия: 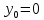 , , 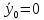 . . По полученным результатам сделать выводы о влиянии сопротивления на вынужденные колебания механической системы с одной степенью свободы.        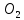 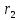 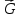 2  Рис.1 Указание 1. Сохраняется вариант, присвоенный при выполнении задания Д23. Указание 2. В тех вариантах, где радиус блока (диска) ( 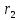 на рис.1)не задан, считать его равным 0,15 м. на рис.1)не задан, считать его равным 0,15 м.Указание 3. Рекомендуется строить графики для интервала времени 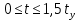 , где время установления , где время установления 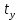 находим из условия a1=0,01A (a1-амплитуда собственных затухающих колебаний, A - амплитуда установившихся вынужденных колебаний в случае n=0,5k). Рекомендуемый интервал времени можно уменьшать или увеличивать, если это позволяет сделать рисунок более наглядным. находим из условия a1=0,01A (a1-амплитуда собственных затухающих колебаний, A - амплитуда установившихся вынужденных колебаний в случае n=0,5k). Рекомендуемый интервал времени можно уменьшать или увеличивать, если это позволяет сделать рисунок более наглядным. Методические указания к выполнению задания Д23В «Исследование влияния сопротивления на вынужденные колебания механической системы с одной степенью свободы» 1) Для составления дифференциального уравнения вынужденных колебаний используем уравнение Лагранжа в форме 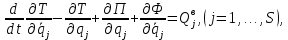 где 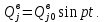 Так как S=1, q=y, то 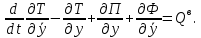 2) Выражения T и П известны из решения задания Д23: 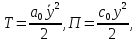 где 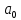 и и 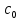 – обобщенные коэффициенты инерции и жесткости, соответственно (уже найдены в Д23). – обобщенные коэффициенты инерции и жесткости, соответственно (уже найдены в Д23). Выражение диссипативной функции Рэлея получали при выполнении задания Д23С: 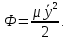 3) Обобщенную возмущающую силу 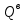 находим по формуле: находим по формуле: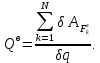 В данном случае мы имеем только одну возмущающую силу – 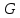 (см. рис.1), поэтому (см. рис.1), поэтому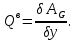 Элементарную работу 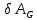 силы силы 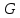 можно записать через ее мощность можно записать через ее мощность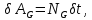 а возможное перемещение (вариацию обобщенной координаты) 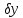 – через обобщенную скорость – через обобщенную скорость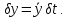 Тогда обобщенную возмущающую силу 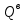 можно найти также по формуле можно найти также по формуле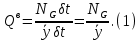 Постоянная сила 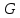 создает момент относительно центра создает момент относительно центра 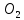 блока 2 (рис.1), являющийся переменным вследствие периодического изменения плеча блока 2 (рис.1), являющийся переменным вследствие периодического изменения плеча 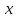 силы силы 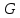 (см. условие задания Д23В) (см. условие задания Д23В)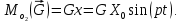 Тогда мощность силы 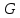 удобно найти через мощность ее момента по известной из курса теоретической механики формуле удобно найти через мощность ее момента по известной из курса теоретической механики формуле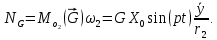 Подставив 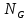 в формулу (1), получим в формулу (1), получим 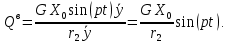 4)Подставляя T, П, Ф и 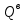 в уравнение Лагранжа, поделив на в уравнение Лагранжа, поделив на 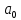 и введя обозначения и введя обозначения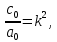 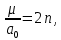 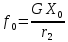 приходим к дифференциальному уравнению 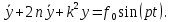 5) Решение аналогичного уравнения было рассмотрено на лекции (задача о вынужденных колебаниях груза на пружине при наличии сопротивления, пропорционального скорости). Записывая по аналогии, получим 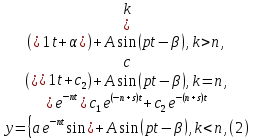 где  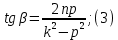 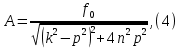 а константы 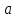 и и 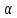 находятся из начальных условий, в данном случае нулевых (см. условие задания Д23В): находятся из начальных условий, в данном случае нулевых (см. условие задания Д23В): 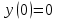 , , 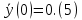 6) В формулах (2-4) 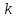 известно из решения Д23, известно из решения Д23, 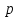 определяется по номеру варианта (см. условие задания Д23В). определяется по номеру варианта (см. условие задания Д23В).Затем для случаев 1-3: а) по (3) находим 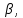 причем, так как причем, так как 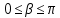 , то , то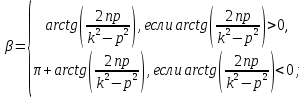 б) по (4) находим  ; ;в) используя начальные условия (5), находим константы a и α, с1 и с2. 7) Находим время установления  (при (при 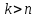 ) и, используя его, строим три кривые ) и, используя его, строим три кривые 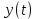 на одном рисунке для случаев 1-3, принимая во внимание указание 3 задания Д23В. на одном рисунке для случаев 1-3, принимая во внимание указание 3 задания Д23В.8) Делаем выводы о влиянии сопротивления на движение системы. |
