Гимназия № 1
Учебно-исследовательская работа
Особенности падения
тел сферической формы в жидкости
Выполнили: Карама Иван
ученики 9 Б класса Политов Антон
Руководитель: Старовиков М.И.
Бийск – 2002
Цель настоящей работы состоит в нахождении вида аналитической функции, выражающей зависимость скорости пластилиновых шарика в глицерине от их радиусов, и экспериментальной проверке справедливости данного соотношения.
Закономерности, которые имеют место при движении тел в жидкости, можно получить из более общих законов классической механики (законов Ньютона). Однако известно, что в реальности каждое физическое явление осуществляется только в связи с другими явлениями. Поэтому исследуемое явление никогда не предстает в «чистом» виде, а законы, которым оно подчиняется, выполняются на практике, и, в том числе, в эксперименте лишь приближенно. В настоящей работе при выводе формулы, выражающей зависимость установившейся (постоянной) скорости движения шариков от их радиуса, мы исходили из следующих упрощающих реальную ситуацию предположений:
движение осуществляется в безграничной среде (не учитывалось «тормозящее» влияние стенок сосуда);
после того, как шарики проходят определенное расстояние (в наших опытах около 10 см), движение их становится равномерным (на самом деле, скорость приобретает установившееся значение лишь на бесконечности);
шарики имеют форму шара (в действительности форма шариков, очевидно, несколько отличается от сферической).
Все эти факторы приводят к тому, что формула, полученная теоретически, не может вполне точно описывать экспериментальные данные. С другой стороны, как известно, никакое измерение не может быть выполнено без погрешностей. В настоящих экспериментах при измерении расстояния, пройденного шариками в глицерине, времени, плотности глицерина и пластилина, размера шарика имели место инструментальные и субъективные погрешности. С учетом отмеченных обстоятельств представляло интерес выяснить, насколько точно (адекватно) «теория» (т.е. формула, выражающая исследуемую зависимость) описывает экспериментальные данные.
Задачи исследования:
Теоретически получить зависимость величины установившейся скорости движения пластилиновых шариков в глицерине от их радиуса.
Спланировать и осуществить эксперимент по измерению времени движения шариков на одном и том же участке сосуда при варьировании радиуса шариков.
Сравнить данные, полученные расчетным путем, с экспериментальными.
Найти число Рейнольдса для всех пластилиновых шариков, убедиться, что обтекание шариков жидкостью является ламинарным.
Определить вязкость глицерина.
Предмет исследования: зависимость скорости пластилиновых шариков в глицерине от их радиусов.
Практическая значимость: мы на опыте доказали, что результаты измерений в пределах погрешностей не отличаются от теоретически рассчитанных.
Определение аналитического вида
исследуемой зависимости
При движении шарика в жидкости с постоянной (установившейся) скоростью, равнодействующая всех действующих на него сил равна нулю. На шарик в рассматриваемом случае действуют сила тяжести Fтяж, архимедова сила Fa и сила вязкого трения Fc. Выразив каждую из сил через определяемые в опыте величины, получим:
 (1) (1)
где R – радиус шарика, ρпл – плотность пластилина, ρгл – плотность глицерина, g – ускорение свободного падения (на широте г. Бийска g = 9,81 м/с2), η – вязкость глицерина, v – установившаяся скорость шарика. При записи уравнения (1) мы использовали формулу Стокса Fc = 6πηRv.
Вид искомой зависимости устанавливается непосредственно из формулы (1):
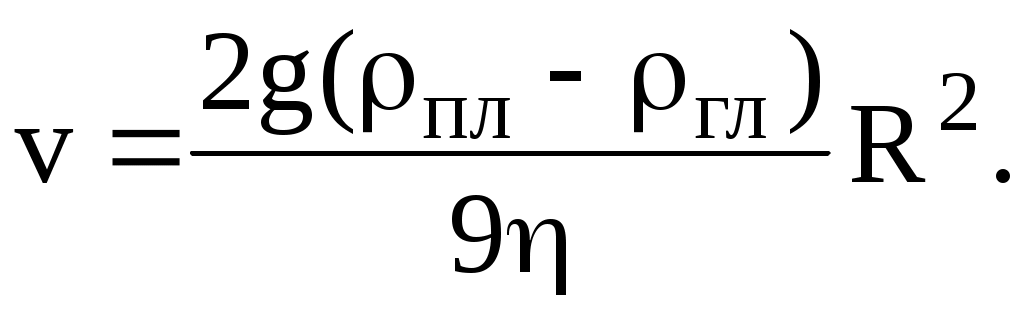 (2) (2)
Как видно, установившееся значение скорости шариков пропорционально квадрату их радиуса.
Результаты эксперимента
И змерение скорости пластилиновых шариков проводилось при их движении в цилиндрическом сосуде с глицерином, рис.1. Наблюдения показали, что в пределах погрешности измерений скорость шариков перестает увеличиваться после того, как они пройдут в глицерине расстояние около 10 см. Именно на таком расстоянии на поверхности цилиндрического сосуда помещалось верхнее резиновое кольцо для отсчета расстояния, пройденного шариками. Нижнее кольцо помещалось непосредственно вблизи дна сосуда. змерение скорости пластилиновых шариков проводилось при их движении в цилиндрическом сосуде с глицерином, рис.1. Наблюдения показали, что в пределах погрешности измерений скорость шариков перестает увеличиваться после того, как они пройдут в глицерине расстояние около 10 см. Именно на таком расстоянии на поверхности цилиндрического сосуда помещалось верхнее резиновое кольцо для отсчета расстояния, пройденного шариками. Нижнее кольцо помещалось непосредственно вблизи дна сосуда.
Для измерения времени движения шариков использовался секундомер СОП пр-2а-3-000, инструментальную погрешность которого Δин t = ± 0,4 с можно считать аддитивной в диапазоне продолжительностей до нескольких минут. Мы полагаем, что в состав указанной погрешности входит и погрешность, обусловленная конечным временем реакции экспериментатора. Измерения диаметра шариков производились с помощью длиннофокусного микроскопа МБС–10, имеющего окулярную шкалу. Принималось, что инструментальная погрешность измерения диаметра шариков составляла ±2 деления шкалы. В зависимости от выбранного увеличения это соответствовало погрешности Δин R = ±0,1 мм при увеличении 2х, Δин R = ±0,05 мм при увеличении 4х Δин R = ±0,03 мм при увеличении 7х.
Для обеспечения точности и достоверности результатов на этапе планирования эксперимента были определены следующие условия проведения измерений:
число изготавливаемых из пластилина шариков должно быть не менее 10, их диаметр должен изменяться от минимально возможного до 0,1 от диаметра сосуда;
перед опусканием в сосуд шарики смачивались глицерином для того, чтобы не допустить прилипания к ним пузырьков воздуха;
расстояние, которое проходят шарики в глицерине, должно быть (в пределах возможного) максимально большим.
Первичные экспериментальные данные и результаты вычисления по этим данным скорости и диаметра шариков представлены в таблице 1. Значения установившейся скорости шариков определялись по формуле v = s/t, где s – пройденное расстояние, t – время движения. Во всех опытах величина s оставалась постоянной, равной 0,340 м. Измерение диаметра шарика предполагает определение положения его левого и правого границ относительно окулярной шкалы. В таблице соответствующие отсчеты обозначены как «отсчет слева» и «отсчет справа». Разность между ними дает число делений, лежащих в пределах диаметра шарика. В связи с тем, что шарики имели не вполне правильную форму, измерения диаметра каждого шарика проводились трижды. За результат измерения принималось среднее арифметическое этих измерений.
Таблица 1
Результаты измерений установившейся скорости падения
шариков и их диаметра
№
шарика
|
Отсчет
слева
|
Отсчет
справа
|
Число
делений
|
Среднее арифметическое числа делений
|
Увеличение объектива микроскопа
|
D, м
|
t.c
|
v, м/с
|
1
|
20
|
163
|
143
|
139,0
|
4
|
0,003475
|
60,4
|
0,0056
|
|
30
|
170
|
140
|
|
|
|
|
|
|
37
|
171
|
134
|
|
|
|
|
|
2
|
46
|
139
|
93
|
96,3
|
2
|
0,004817
|
32,7
|
0,0104
|
|
45
|
146
|
101
|
|
|
|
|
|
|
41
|
136
|
95
|
|
|
|
|
|
3
|
17
|
141
|
124
|
112,0
|
4
|
0,002800
|
76,9
|
0,0044
|
|
35
|
151
|
116
|
|
|
|
|
|
|
40
|
136
|
96
|
|
|
|
|
|
4
|
36
|
167
|
131
|
127,3
|
2
|
0,006367
|
21,6
|
0,0158
|
|
26
|
150
|
124
|
|
|
|
|
|
|
29
|
156
|
127
|
|
|
|
|
|
5
|
50
|
139
|
89
|
89,7
|
1
|
0,008967
|
11,6
|
0,0294
|
|
47
|
136
|
89
|
|
|
|
|
|
|
50
|
141
|
91
|
|
|
|
|
|
6
|
29
|
153
|
124
|
120,0
|
1
|
0,012000
|
8,4
|
0,0405
|
|
39
|
156
|
117
|
|
|
|
|
|
|
25
|
144
|
119
|
|
|
|
|
|
7
|
39
|
126
|
87
|
88,7
|
4
|
0,002217
|
151,7
|
0,0022
|
|
40
|
130
|
90
|
|
|
|
|
|
|
49
|
138
|
89
|
|
|
|
|
|
8
|
17
|
175
|
158
|
163,3
|
4
|
0,004083
|
50,8
|
0,0067
|
|
9
|
169
|
160
|
|
|
|
|
|
|
8
|
180
|
172
|
|
|
|
|
|
9
|
37
|
148
|
111
|
111,7
|
2
|
0,005583
|
26,7
|
0,0127
|
|
36
|
149
|
113
|
|
|
|
|
|
|
33
|
144
|
111
|
|
|
|
|
|
10
|
27
|
167
|
140
|
138,0
|
2
|
0,006900
|
19,2
|
0,0178
|
|
26
|
164
|
138
|
|
|
|
|
|
|
24
|
160
|
136
|
|
|
|
|
|
11
|
30
|
140
|
110
|
110,3
|
1
|
0,011033
|
9,4
|
0,0362
|
|
33
|
143
|
110
|
|
|
|
|
|
|
26
|
137
|
111
|
|
|
|
|
|
12
|
40
|
145
|
105
|
105,3
|
4
|
0,002633
|
110,7
|
0,0031
|
|
41
|
145
|
104
|
|
|
|
|
|
|
39
|
146
|
107
|
|
|
|
|
|
Из формулы (2) видно, что график зависимости v(R) должен быть линейным, если по горизонтальной оси откладывать величину R2. Угловой коэффициент a этой прямой, согласно уравнению (2), равен
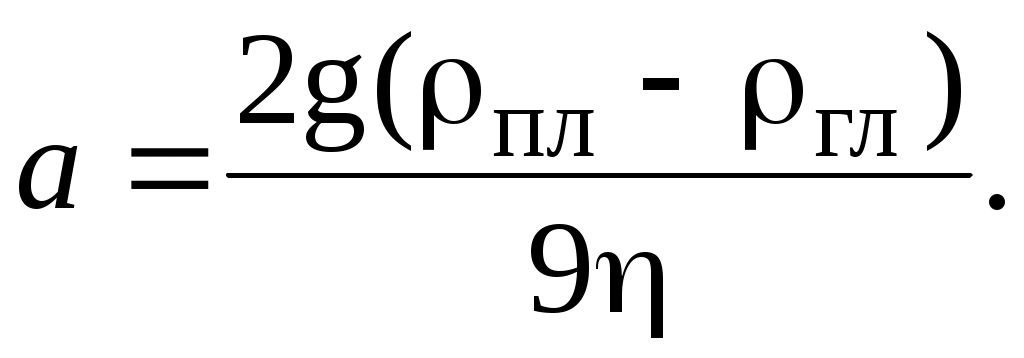
Определив из графика экспериментальных данных методом наименьших квадратов величину углового коэффициента а, можно затем вычислить значение коэффициента вязкости глицерина по формуле
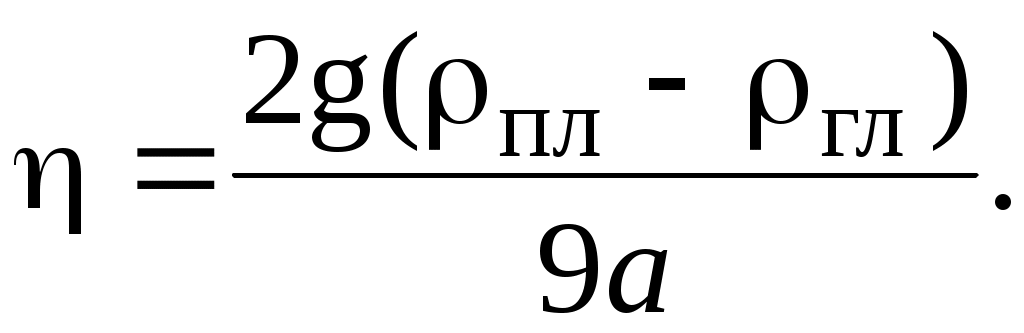 (3) (3)
В этом состоит метод измерения коэффициента вязкости в настоящей работе.
Данные для построения графика в координатных осях v – R2 приведены в таблице 2, а сам точечный график – на рис.2. На координатной плоскости методом наименьших квадратов построен также линейный график аппроксимирующей функции.
Таблица 2
Данные для построения графика зависимости v(R2)
V, м/с
|
R, м
|
R2, м2/c2
|
0,002242
|
0,001109
|
1,2288E-06
|
0,003072
|
0,001167
|
1,3607E-06
|
0,004422
|
0,001400
|
1,9600E-06
|
0,005634
|
0,001738
|
3,0189E-06
|
0,006694
|
0,002042
|
4,1677E-06
|
0,010389
|
0,002409
|
5,8009E-06
|
0,012729
|
0,002792
|
7,7925E-06
|
0,015770
|
0,003184
|
1,0135E-05
|
0,017755
|
0,003450
|
1,1903E-05
|
0,029437
|
0,004484
|
2,0102E-05
|
0,036117
|
0,005517
|
3,0432E-05
|
И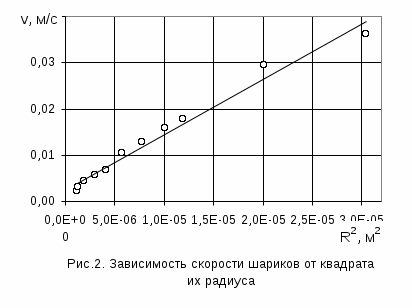
з графика видно, что в целом точки хорошо ложатся на прямую линию, что подтверждает применимость формулы (2) к описанию имеющейся совокупности экспериментальных данных. В то же время, на наш взгляд, качество выборки возрастет, если из нее исключить первую и последнюю точки. Скорей всего, заниженное значение скорости самого большого шарика объясняется влиянием стенок сосуда. Как отмечено выше, сила вязкого трения в ограниченной стенками сосуда жидкости больше, чем в бесконечной. При этом различие возрастает с увеличением размера тела. Что касается данных для шарика самого маленького размера, то, возможно, меньшее, чем можно было бы ожидать, значение скорости объясняется тормозящим влиянием прилипшего к нему пузырька воздуха.
Г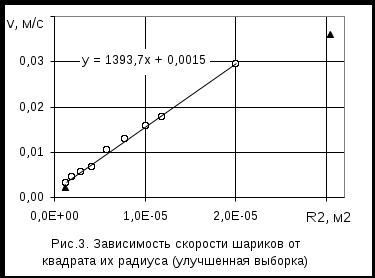 рафик, построенный по данным улучшенной выборки, приведен на рис.3. На координатной плоскости графика сохранены также 2 исключенные из исходного ряда данных точки (они обозначены треугольниками). Сопоставление графиков, приведенных на рис.2 и на рис.3 показывает, что после исключения двух точек оставшиеся точки группируются около прямой линии более тесно. На координатную плоскость графика выведено уравнение прямой, наилучшим образом описывающей экспериментальные данные. Обращаем внимание на то, что свободный член в этом уравнении близок к нулю (составляет всего 0,0015 м/с), что хорошо согласуется с уравнением (2). рафик, построенный по данным улучшенной выборки, приведен на рис.3. На координатной плоскости графика сохранены также 2 исключенные из исходного ряда данных точки (они обозначены треугольниками). Сопоставление графиков, приведенных на рис.2 и на рис.3 показывает, что после исключения двух точек оставшиеся точки группируются около прямой линии более тесно. На координатную плоскость графика выведено уравнение прямой, наилучшим образом описывающей экспериментальные данные. Обращаем внимание на то, что свободный член в этом уравнении близок к нулю (составляет всего 0,0015 м/с), что хорошо согласуется с уравнением (2).
Для того, чтобы можно было сделать обоснованное заключение о том, что экспериментальные точки действительно тесно группируются около прямой линии, необходимо указать на графике погрешности экспериментального определения величин v и R2.
П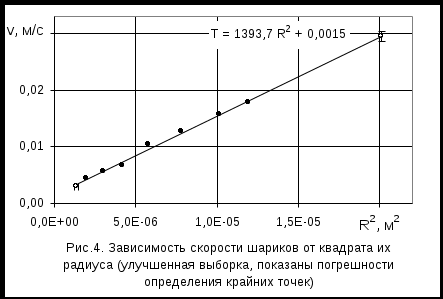 огрешность определения скорости шариков не является постоянной. Она увеличивается с ростом радиуса шариков и составляет 0,000008 м/с для шарика минимального радиуса и 0,0009 м/с – для максимального. Из графика видно, что для шариков большого радиуса линия регрессии проходит в пределах границ неопределенности величины скорости. огрешность определения скорости шариков не является постоянной. Она увеличивается с ростом радиуса шариков и составляет 0,000008 м/с для шарика минимального радиуса и 0,0009 м/с – для максимального. Из графика видно, что для шариков большого радиуса линия регрессии проходит в пределах границ неопределенности величины скорости.
Погрешность определения скорости самого маленького шарика весьма мала. Поэтому для шарика минимального радиуса вычислена и указана на графике Х-погрешность, т.е. погрешность определения величины R2. Она составляет 0,00000012 м2. Эта величина тоже невелика, для того, чтобы увидеть, проходит или не проходит график в пределах данной погрешности, на рис.5 показан начальный участок графика в увеличенном масштабе. Как видно, наилучшая прямая не попадает в интервал погрешности R2, однако проходит очень близко от него.
И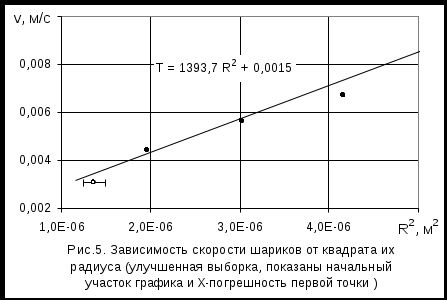 з проведенного анализа можно заключить, что, в целом, в пределах погрешностей определения экспериментальные точки, в целом, хорошо ложатся на прямую линию. Тем самым, экспериментально подтверждается справедливость формулы (2). з проведенного анализа можно заключить, что, в целом, в пределах погрешностей определения экспериментальные точки, в целом, хорошо ложатся на прямую линию. Тем самым, экспериментально подтверждается справедливость формулы (2).
Для определения вязкости глицерина по формуле (3) необходимо иметь данные о плотности глицерина и плотности пластилина. Плотность глицерина определялась с помощью ареометра, инструментальная погрешность которого составляет 10 кг/м2. С учетом погрешности отсчета (5 кг/м2) результирующая погрешность определения плотности составит 11 кг/м2. Результат измерения запишется в виде ρгл = (1220 ± 11) кг/м2, ερ гл = 0,9 %.
Плотность пластилина определялась косвенным способом с использованием формулы ρпл = m/V, где m – масса куска пластилина, V – его объем. Масса пластилина измерялась с помощью аналитических весов, а объем - с помощью мензурки. Конечный результат измерения плотности составил величину ρпл = (1305 ± 110) кг/м2, ερ пл = 8 %.
При вычислении вязкости глицерина использовалось значение ускорения свободного падения, которое на широте г. Бийска составляет g = (9,81 ± 0,05) м/с2 εg = 0, 5 %.
Применяя формулу (3) для нахождения вязкости глицерина, получим:
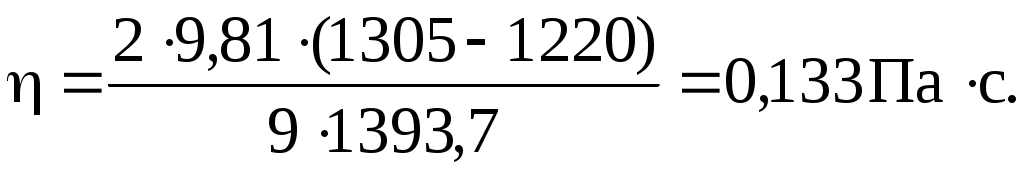
Полученное значение согласуется с табличным.
Погрешность определения углового коэффициента прямой v(R2) можно оценить, вычислив отношение Δvмин/R2 = 0,0009/3,04·10-5 = 30. По отношению к величине углового коэффициента это составит εугл = (30/1394)·100 % ≈ 2 %. Данная величина заметно (в 4 раза) меньше погрешности определения плотности пластилина. Поэтому вкладом ее в результирующую погрешность вязкости можно пренебречь, как и вкладом всех других величин, входящих в формулу (3). С учетом этого погрешность вязкости может быть оценена по формуле:
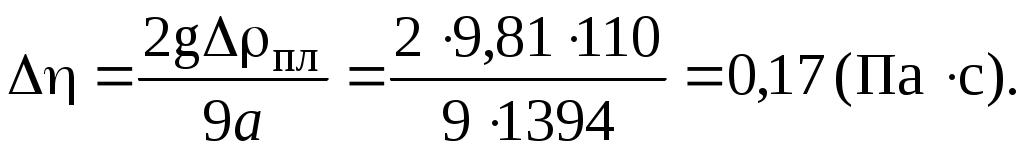
Таким образом, η = (0,13 ± 0,17) Па·с. Получено, что погрешность определения вязкости превышает найденное действительное ее значение. Этот неудовлетворительный результат объясняется недостаточной точностью определения плотности пластилина.
Основные результаты и выводы
В процессе равномерного движения шарика в жидкости сумма всех действующих на него сил равна нулю. Из этого условия в настоящей работе найдена формула, выражающая зависимость величины установившейся скорости шариков от их радиусов. Эта зависимость имеет вид v R2.
Выполнена серия измерений установившейся скорости падения пластилиновых шариков различных радиусов в глицерине. По полученным экспериментальным данным построен точечный график в координатных осях v – R2, методом наименьших квадратов через эти точки проведена наилучшая прямая. Установлено, что экспериментальные точки тесно (в основном, в пределах погрешностей) группируются около прямолинейного графика. На этом основании сделан вывод о применимости полученной формулы к описанию явления равномерного движения шариков в глицерине.
Выяснено, что для шариков большого диаметра (более 1 см) зависимость v R2 выполняется хуже, чем для шариков меньшего размера. При этом отклонение точек от прямолинейного графика увеличивается с возрастанием диаметра шариков. Мы объясняем это возрастание силы вязкого влиянием стенок сосуда. (Использовавшаяся при выводе формулы v(R) формула Стокса справедлива для бесконечной среды.)
По величине углового коэффициента графика зависимости v(R), построенного в координатных осях v R2 определена величина вязкости глицерина η = (0,13 ± 0,17) Па·с. Хотя полученное значение согласуется с табличным, оценка погрешности его определения оказалась недопустимо большой. Для повышения точности определения вязкости необходимо обеспечит меньшую погрешность определения плотности пластилина.
Литература
Савельев И.В. Курс физики. Т.1. Механика. Молекулярная физика. – М.: Наука, 1989. – 352 с.
Старовиков М.И. Исследовательский учебный эксперимент по физике с компьютерной поддержкой. – Бийск: НИЦ БПГУ, 2002. – 128 с.
|
 Скачать 158.5 Kb.
Скачать 158.5 Kb.
 змерение скорости пластилиновых шариков проводилось при их движении в цилиндрическом сосуде с глицерином, рис.1. Наблюдения показали, что в пределах погрешности измерений скорость шариков перестает увеличиваться после того, как они пройдут в глицерине расстояние около 10 см. Именно на таком расстоянии на поверхности цилиндрического сосуда помещалось верхнее резиновое кольцо для отсчета расстояния, пройденного шариками. Нижнее кольцо помещалось непосредственно вблизи дна сосуда.
змерение скорости пластилиновых шариков проводилось при их движении в цилиндрическом сосуде с глицерином, рис.1. Наблюдения показали, что в пределах погрешности измерений скорость шариков перестает увеличиваться после того, как они пройдут в глицерине расстояние около 10 см. Именно на таком расстоянии на поверхности цилиндрического сосуда помещалось верхнее резиновое кольцо для отсчета расстояния, пройденного шариками. Нижнее кольцо помещалось непосредственно вблизи дна сосуда.
 рафик,
рафик,  огрешность определения скорости шариков не является постоянной. Она увеличивается с ростом радиуса шариков и составляет 0,000008 м/с для шарика минимального радиуса и 0,0009 м/с – для максимального. Из графика видно, что для шариков большого радиуса линия регрессии проходит в пределах границ неопределенности величины скорости.
огрешность определения скорости шариков не является постоянной. Она увеличивается с ростом радиуса шариков и составляет 0,000008 м/с для шарика минимального радиуса и 0,0009 м/с – для максимального. Из графика видно, что для шариков большого радиуса линия регрессии проходит в пределах границ неопределенности величины скорости. з проведенного анализа можно заключить, что, в целом, в пределах погрешностей определения экспериментальные точки, в целом, хорошо ложатся на прямую линию. Тем самым, экспериментально подтверждается справедливость формулы (2).
з проведенного анализа можно заключить, что, в целом, в пределах погрешностей определения экспериментальные точки, в целом, хорошо ложатся на прямую линию. Тем самым, экспериментально подтверждается справедливость формулы (2).