Творческая работа. Лист Мёбиуса.. История. Август Фердинанд Мёбиус
 Скачать 286.62 Kb. Скачать 286.62 Kb.
|
|
Лист Мёбиуса. История.  Август Фердинанд Мёбиус (1790-1868) - ученик великого Гаусса, известный геометр, профессор Лейпцигского университета, директор обсерватории. Существует несколько мнений о появлении легендарной ленты Мёбиуса: 1. Первая версия утверждает, что знаменитую ленту профессор изобрел когда поступал на повара в кулинарный университет. 2. Вторая версия утверждает, что ленту профессор открыл в конце своей жизни и не дождался момента опубликования статьи. 3. Третья версия утверждает, что одновременно с Мёбиусом ленту открыл еще один учёный. 4. Четвертая же предполагает, что натолкнула Мёбиуса на создание своего творения служанка, неправильно слепившая концы ленты. Так, или иначе, сейчас у нас есть незамысловатая, но поистине удивительная лента Мёбиуса - один из символов бесконечности. Лента Мёбиуса Лист Мёбиуса (ле́нта Мёбиуса, петля́ Мёбиуса) — топологический объект, простейшая неориентируемая поверхность с краем. Попасть из одной точки этой поверхности в любую другую можно, не пересекая края. Пример ленты Мёбиуса:   "Сделать" Ленту Мёбиуса несложно, я бы даже сказала просто. Поэтому удобнее просто рассмотреть ленту Мебиуса поближе. Берем бумажную полоску, перекручиваем полоску в пол-оборота поперек (на 180 градусов) и склеиваем концы:  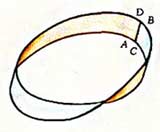 Так почему же ленту Мёбиуса называют "одним из символов бесконечности"? Данный лист обладает интересным свойством: Ставим в каком-нибудь месте на полоске точку фломастером. А теперь прочерчиваем вдоль всей нашей ленты линию, пока вам не встретится вновь ваша точка. Вам нигде не пришлось переходить через край – это и называется односторонней поверхностью. Посмотрите, как интересно проходит прочерченная вами линия: она то внутри кольца, то снаружи! А теперь измерьте длину этой линии - от точки до точки. Удивляетесь? Она оказывается в два раза длиннее первоначальной полоски бумаги! Так и должно быть, ведь у вас в руках лента Мебиуса! А у ленты Мебиуса есть только одна сторона, и мы опять скажем – это односторонняя поверхность с краем. А если по этой черте заставить ползти, не сворачивая, муравья, то вы получите копию картины художника Мориса Эшера. Бедный муравей на бесконечной дороге! А можно сделать две немного разные ленты Мебиуса: у одной перекручивать перед склейкой полоску по часовой стрелке, а у другой – против часовой стрелки. Так различаются правая и левая ленты Мебиуса. Несколько сюрпризов: 1. Разрежьте ленту Мебиуса вкруговую по центральной линии. Не бойтесь, она не развалится на две части! Лента развернется в длинную замкнутую ленту, закрученную вдвое больше, чем первоначальная. Почему лента Мебиуса при таком разрезе не распадается на отдельные части? Разрез не касался края ленты, поэтому после разреза край (а значит и вся полоска бумаги) останется целым куском. 2. Полученную после первого опыта ленту Мебиуса (закрученную вдвое больше, чем первоначальная, т.е. на 360 градусов) вновь разрежьте по ее центральной линии. Что получится? У вас в руках окажутся теперь две одинаковые, но сцепленные между собой ленты Мебиуса. 3. Сделайте новую ленту Мебиуса, но перед склейкой поверните ее не один раз, а три раза (не на 180 градусов, а на 540). Затем разрежьте ее вдоль центральной линии. Что получилось? У вас должна получиться замкнутая лента, завитая в узел трилистника, т.е. в простой узел с тремя самопересечениями. 4. Если вы сделаете ленту Мебиуса с еще большим числом полуоборотов перед склейкой, то получатся неожиданные и удивительные фигуры, называемые парадромными кольцами. 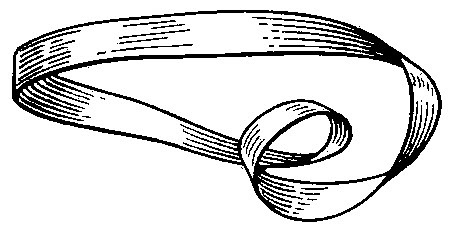 5. Если разрезать ленту Мебиуса, не посередине, а отступая от края приблизительно на треть её ширины, то получатся две сцепленные ленты, одна — более короткая лента Мебиуса, и другая — длинная лента Мебиуса с двумя полуоборотами. Лента Мёбиуса в нашей жизни Научные открытия нередка вдохновляют поэтов на написание прекрасных произведений, и нашего героя не обошла данная традиция. Взять к примеру стихотворение Н.Ю. Ивановой: Лист Мебиуса - символ математики, Что служит высшей мудрости венцом… Он полон неосознанной романтики: В нем бесконечность свернута кольцом. В нем – простота, и вместе с нею – сложность, Что недоступна даже мудрецам: Здесь на глазах преобразилась плоскость В поверхность без начала и конца. Здесь нет пределов, нет ограничений, Стремись вперед и открывай миры, Почувствуй силу новых ощущений, Прими познанья высшего дары: Познай любовь и ненависть изведай, Низвергнись в ад – тотчас увидишь рай. Ты в одночасье насладись победой И горечь пораженья испытай. На грани бесконечного блаженства Испытывая суеверный страх, Найдешь свой путь. Достигнув совершенства, Окажешься в таинственных мирах. И, вдохновленный этим дерзновеньем, По экспоненте поднимаясь в высь, Ты ощутишь восторг освобожденья, Почувствуешь, как возникает Мысль. Покажется, что распростерлась Вечность, Что взломан Мироздания пароль. И вдруг твое стремленье в бесконечность Тебя вернет к исходной точке: в ноль. Как о порог, об этот ноль споткнешься. Но как бы ни был прежний путь тернист, Вновь выбирай (и ты не ошибешься!) Путь в бесконечность – Мёбиуса лист. 3. Лист Мёбиуса в Астрономии Неизведанная Вселенная Если космический корабль полетит все время прямо, никуда не сворачивая, то будет ли он все более удаляться от Земли? "Не обязательно, -- решил Эйнштейн. -- Корабль может вернуться, даже если он все время будет лететь прямо". Чтобы понять парадокс Эйнштейна, начнем с несчастного пойнтландца. Вся его вселенная -- это одна-единственная точка, имеющая нуль измерений. Обитающий на одномерной линии лайнландец подобен червяку, ползущему по канату: если канат бесконечен, то он может путешествовать сколь угодно далеко как в одну, так и в другую сторону. Но если канат замкнут наподобие окружности, то вселенная нашего лайнландца неограниченна, хотя и имеет конечную длину. В какую бы сторону ни полз червяк, он непременно вернется в исходную точку. Флатландец обитает на двумерной поверхности. Если его вселенная -- бесконечная плоскость, то он может путешествовать на любые расстояния в любом направлении. Но если поверхность, на которой он обитает, замкнута наподобие сферы, то она также неограниченна и конечна. В какую бы сторону ни отправился флатландец, двигаясь все время прямо и никуда не сворачивая, он непременно вернется туда, откуда начал свой путь. Мы с вами "солидландцы", обитающие в трехмерном мире. Возможно, наш мир простирается бесконечно далеко в каждом из направлений. Но, может быть, наша Вселенная изогнута в пространстве большего числа измерений и потому неограниченна и конечна? В такой Вселенной, как и полагал Эйнштейн, космический корабль, все время летящий прямо, мог бы вернуться к месту старта. Когда флатландец совершает кругосветное путешествие по сфере, он как бы движется по полоске, склеенной в кольцо без перекручивания. Но если флатландец путешествует по листу Мёбиуса, то происходит нечто странное. Полоборота, на которые перекручено полотно листа, как бы переворачивают флатландца на другую сторону: вернувшись в исходную точку, он обнаруживает у себя сердце не слева, а справа! Если наше пространство перекручено наподобие листа Мёбиуса, то вернувшийся на Землю астронавт может оказаться собственным зеркальным отражением. Астрономы пока не пришли к единому мнению относительно того, замкнута ли наша Вселенная, как полагал Эйнштейн, или открыта. Ответ на этот вопрос зависит от того, какова масса Вселенной. Согласно общей теории относительности, масса приводит к искривлению пространства -- чем больше масса, тем больше кривизна пространства. Большинство специалистов по современной космологии считают, что массы Вселенной недостаточно для столь сильного искривления пространства, которое привело бы к его замыканию. Но вопрос пока остается открытым, поскольку ни природа-вещества, ни распределение его плотности во Вселенной не известны. Не исключено, что во Вселенной имеется "скрытая масса", вполне достаточная для замыкания пространства. (Например, подозревают, что нейтрино обладают положительной массой покоя, в то время как раньше их масса покоя считалась равной нулю.) Не существует никаких данных, позволяющих утверждать о том, будто наше пространство перекручено, как лист Мёбиуса. Тем не менее ученые, занимающиеся космологией, охотно рассматривают различные модели пространства, в том числе и модели с кручением. Для того чтобы понять, каким образом флатландец, совершив кругосветное путешествие по листу Мёбиуса, переходит в свое зеркальное отражение, важно не упускать из виду одно существенное обстоятельство: нулевую толщину листа Мёбиуса. Любая бумажная модель листа Мёбиуса в действительности представляет собой объемное тело, так как бумага имеет конечную толщину. Мы же должны исходить из предположения о том, что идеальный лист Мёбиуса имеет нулевую толщину. Плоская фигура, начерченная на идеальном листе Мёбиуса, напоминает фигуру, начерченную чернилами, которые проходят сквозь бумагу, делая контур видимым с двух сторон: она начерчена одновременно с двух "сторон" листа, а не только с одной "стороны", как бы погружена в его поверхность пулевой толщины. Вернувшись в исходное положение после обхода листа Мёбиуса, такая фигура переходит в свое зеркальное отражение. Разумеется, при повторном обходе она вновь принимает свой первоначальный вид. Аналогичным образом астронавт, вернувшись из кругосветного путешествия в пространстве с кручением, оказался бы зеркальным двойником самого себя и, лишь совершив повторное кругосветное путешествие, смог бы "прийти в себя". Если вас заинтересовали парадоксальные свойства листа Мёбиуса, то вам, возможно, покажутся интересными две другие не менее парадоксальные поверхности -- бутылка Клейна и проективная плоскость -- и.вы захотите изучить их подробнее. Обе поверхности односторонние, но в отличие от листа Мёбиуса не имеют краев. Бутылка Клейна тесно связана с листом Мёбиуса, так как, разрезав ее пополам, мы можем получить два зеркально-симметричных листа Мёбиуса. Флатландец, обитающий на поверхности бутылки Клейна или на проективной плоскости, совершив кругосветное путешествие, переходит в свое зеркальное отражение (см. главу 2 моей "Шестой книги математических игр" из журнала Scientific American) [Gardner М. Sixth Booh of Mathematical Games from Scientific American.-San Francisco, 1971.]. Классической книгой о жизни в двумерном пространстве по праву считается "Флатландия" Эдвина Э. Эббота. Ее продолжение -- "Сферландию" -- написал Дионис Бюргер [Эбботт Э. Флатландия. Бюргер Д. Сферландия. - M.: Мир, 1976.]. Возможно, вам понравится фантастический рассказ Г. Уэллса "История Платтнера" -- о человеке, побывавшем в четвертом измерении и вернувшемся на Землю своим зеркальным двойником -- с сердцем, расположенным справа. Лист Мёбиуса в философии «Парадокс лгуна» Лента Мёбиуса - это кольцо, которое в каждой точке имеет соответственно по две составляющие протяжённость грани. Протяжённости идут параллельно кольцу. Конец одной грани соединяется с началом другой. Так две грани образуют второе кольцо, дважды обёрнутое вокруг основного. Поэтому бессмысленно различать грань с её противоположностью в контексте всего пространства граней точек основного кольца. Истину или ложь утверждает человек, который говорит «я лгу», и больше ничего не говорит? Истину или ложь утверждает человек, который говорит «я лгу», и больше ничего не говорит? Вот, к примеру, вариант Эвбулида: Критянин Эпименид сказал: «Все критяне лжецы». Эпименид сам критянин. Следовательно, он лжец. Если Эпименид лгун, тогда его заявление, что все критяне лгуны – ложно. Значит, критяне не лгуны. Между тем Эпименид, как определено условием, – критянин, следовательно, он не лгун, и поэтому его утверждение «все критяне лгуны» – истинно. Таким образом, мы пришли к взаимоисключающим предложениям. Одно из них утверждает, что высказывание «все критяне лгуны», является ложным, а другое, наоборот, квалифицирует это же высказывание как истинное. Притом как в одном, так и в другом случае наши рассуждения логически строги, в них нет ни намеренных, ни непреднамеренных ошибок. Так где же истина? Было приложено немало усилий объяснить этот странный результат. Имеется, например, такое решение. Почему мы должны считать, что Эпименид говорит одну только ложь и никогда не говорит правды? Точно так же тот, кто считается правдивым, разве всегда утверждает лишь правду? В практике общения ложное обычно перемешано с истиной, и мы не найдем такого отпетого лгуна, который только бы лгал. Его легко изобличить, и тогда понимай все, что им сказано, наоборот. В действительности, однако, положение гораздо сложнее. Парадоксу посвящена обширная литература. Он на самом деле вызывает недоумение. Легенда утверждает даже, что древнегреческий философ Кронос, испытав неудачу в попытках решить парадокс, от огорчения умер, а еще один философ, Филипп Косский, покончил жизнь самоубийством. С тех пор внимание к парадоксу лжеца не затухало. Оно лишь принимало новые формы, обнаруживало новые оттенки. Особенно сильная волна интереса к нему, как и другим парадоксам, была вызвана событиями, разыгравшимися в математике на рубеже XIX - XX столетий. На этот раз к парадоксам подошли основательнее, во всеоружии достижений логики, математики и философии, полученных к тому времени. Взгляд логика: Если А лжец, то, значит, он врет, т.е. в действительности он правдолюбец. Но тогда мы приходим к противоречию. Если же А правдолюбец, т.е. говорит правду, то в действительности он лжец, а это опять противоречие. Таким образом, в этой головоломке не существует непротиворечивого варианта "распределения ролей", т.е. не существует модели в том смысле, который придается ей в математической логике. Оказывается… Лента Мёбиуса - прекрасный пример, что парадокс лжеца не бесмысленен. У нас есть две части - каков человек и какова его фраза, каждая имеющее по две составляющие - лживое/правдивое. С одной стороны протяжённости соединяются тем, что человек и его слова по правдивости одинаковы. С другой стороны соединяются тем, что как слова действуют, так и есть. Части образуют кольцо. При этом составляющие частей тоже замыкаются в одно сложенное вдвое кольцо. Кольцо составляющих означает замкнутость вариантов решения, а значит, невозможность выведения ответа. Предложив сложенное вдвое кольцо(в форме двух протяжённостей с перекрёстным соединением) в контексте требования отделить обороты друг от друга, мы признаём, что такие задачи, которые не имеют решения, существуют. Другое дело, что такие задачи ставятся в тех условиях, в которых уже должно быть известно, что они не имеют решения (кольцо не делится на несколько колец, только на части). А это значит их постановка бессмысленна, если только не считать, что смысл - обращение внимания решающего на причину бессмысленности. Подумайте вечерком… Встречаются два человека, А и В, один из который правдолюбец, а другой — лжец. А говорит: "Либо я лжец, либо В правдолюбец". Кто из этих двоих правдолюбец, а кто лжец? Встречаются три человека, А, В и С. А и говорит: "Все мы лжецы", а В отвечает: "Только один из нас правдолюбец". Кто из этих троих правдолюбец, а кто лжец? Встречаются три человека, А, В и С. Четвертый, проходя мимо, спрашивает А: "Сколько правдолюбцев среди вас?" А отвечает неопределенно, а В отвечает: "А сказал, что среди нас есть один правдолюбец". Тут в разговор вступает С и добавляет: "В врет!" Кем, по-вашему, являются В и С? ТЕХНИКА Кинолента  В 1923 году выдан патент изобретателю Ли де Форсу, который предложил записывать звук на киноленте без смены катушек, сразу с двух сторон. Кассета  Придуманы кассеты для магнитофона, где лента перекручивается и склеивается в кольцо, при этом появляется возможность записывать или считывать информацию сразу с двух сторон, что увеличивает ёмкость кассеты и соответственно время звучания. Автомобиль Toyota MOB  Боллид Мёбиуса выполнен испанским дизайнером Хорхе Марти Видала и сочетает в себе красоту и загадку ленты Мёбиуса. Уникальная форма кузова обеспечивает гоночной машине хорошую аэродинамику Матричный принтер  Во многих матричных принтерах красящая лента также имеет вид листа Мёбиуса для увеличения её ресурса. Резистор Мёбиуса 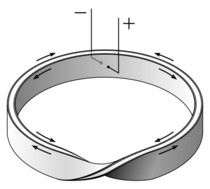 Это недавно изобретённый электронный элемент, который не имеет собственной индуктивности. Шлифовальная лента  В 1969 году советский изобретатель Губайдуллин предложил бесконечную шлифовальную ленту в виде листа Мёбиуса. АРХИТЕКТУРА Здание библиотеки  В настоящее время рассматривается проект постройки библиотеки в виде листа Мёбиуса в Казахстане. Изгибы здания образуют лист Мёбиуса, таким образом внутреннее пространство переходит во внешнее и обратно; подобным образом стены переходят в крышу, а крыша трансформируется обратно в стены. Естественный свет проникает во внутренние коридоры сквозь геометрические отверстия во внешней оболочке, создавая прекрасно освещённые пространства, идеальные для чтения. Аттракционы  Аттракцион “Американские горки” напоминает форму листа Мебиуса. В Москве находятся самые большие в мире американские горки инвертированного типа, где человек сидит в подвешенном кресле, а его ноги находятся в воздухе. Скорость - 81 км/ч, высота 30 м. Высота, по сравнению с зарубежными аналогами, невелика, но это с лихвой окупается обилием спиралей, колец и мёртвых петель. ЖИВОПИСЬ Граффити  Современная лента Мёбиуса нарисована на одной из стен в Праге, Чехия. По ленте двигаются два типа машин: танки и строительно-дорожная техника. Символ современной цивилизации: разрушаем-строим-разрушаем-строим.. ОДЕЖДА И ОБУВЬТуфли  Созданная в 2003 году архитектором Рэм Ди Колхаазом и обувщиком Галахадом Кларком компания United Nude специализируется на выпуске инновационной дизайнерской обуви. Одной из наиболее удачных разработок компании являются туфли Mobius, названные так в честь геометра Августа Мебиуса и его идеи односторонней поверхности. Идея туфель такова: кожаный верх туфель и подошва представляют собой единую ленту, закрученную определенным образом. Шарф Мёбиуса  Инетресная вещь шарф Мёбиуса появивщаяся в гардеробах 21 века. Шарф Мёбиуса можно сделать самому связав концы шарфа на перекрутив на один оборорт. МЕБЕЛЬ Стол Мёбиуса  Стол с одной поверхностью, за которым можно стоять, сидеть и на котором можно удобно лежать. Книжная полка Infinity  Дизайнер Джоб Келевий сломал форму, когда разрабатывал свой книжный шкаф Инфинити. Используя математическую концепцию Лемниската, и что-то похожее на ленту Мебиуса, в полке Инфинити дизайнер воплотил физическое представление о бесконечности. Это значит, что если вы прочитали все книги с этой полки, считайте, что вы постигли всю бесконечность литературы. Диван Мёбиуса  Родившееся под девизом "Двойное кресло - двойное удовольствие", кресло-диван Moebius Double Armchair создано дизайнером Gaеtan Van de Wyer из Бельгии и несет в себе свежее видение мебели для влюбленных. ПАРФЮМ Духи Bugatti  Компания Bugatti начала выпуск не только сверхдорогих автомобилей (модель Veyron стоит 1,3 млн. евро), но и… духов. каждый флакончик, сделанный из хрусталя и покрытый настоящим золотом выполнен в виде необычного листа Мёбиуса, который имеет лишь одну сторону. Цена духов Bugatti составляет 3500 евро. Духи Loewe Quzas, Quizas, Quizas  Осенью 2011 года вышла багровая версия аромата, флакон которой обернут лентой Мебиуса – символом круговорота страстей в природе. Богатство композиции состоит из свежести азиатских апельсинов, бергамота, красных ягод, продолжается цветочным сердцем из магнолии, фрезии и лепестков апельсина, и завершается композицией из чувственного шлейфа кашмирового дерева, золотой амбры и ветивера. Духи UFO Limited Edition, Kenzo  Презентация аромата Kenzo состоялась в 2009 году на ретроспективной выставке работ Рона Арада (Ron Arad) в парижском Центре Помпиду. Именно этот художник и архитектор придумал космический дизайн флакона в виде ленты Мебиуса. Он разработан так, чтобы точь-в-точь поместиться в ладонь. Unidentified Fragrance Object, или «Неопознанный ароматический объект» существует в количестве всего 180 экземпляров и стоит $188. СПОРТ Ручной эспандер "Робур"  Одна из любимых вещей всех школьных учителей физкультуры, которая по их собственному выражению «тренирует не только мышцы кисти, но и мышцу мозга". Кистевой эспандер от студии Артемия Лебедева повторяет форму ленты Мёбиуса. Отличное средство для снятия стресса, размышлений о бесконечности и просто полезный способ занять руки. |
