Бутенас, МХ-20. История появления комплексных чисел

• Название: История появления комплексных чисел
• Дата: 10.01.2022
• Размер: 247.5 Kb.
• Имя файла: Бутенас, МХ-20.doc
• Тип: Документы; #327164

Министерство образования и науки Кузбасса

Государственное профессиональное образовательное учреждение

«Кузнецкий индустриальный техникум»


Специальность/профессия

15.02.10 Мехатроника и мобильная

робототехника (по отраслям)

ИНДИВИДУАЛЬНЫЙ ПРОЕКТ

по дисциплине:

«Математика»

по теме:

«История появления комплексных чисел»

Студент

Бутенас Олег Викторович

подпись ФИО

Преподаватель

Назарова Надежда Николаевна

подпись ФИО

Новокузнецк 2021

Оглавление
Введение 3

Глава 1. История возникновения комплексных чисел 4

1.1 Развитие понятия о числе 4

1.2 На пути к комплексным числам 5

1.3 Утверждение комплексных чисел в математике 7

Глава 2. Комплексные числа и их свойства 10

2.1 О комплексных числах 10

2.2 Геометрическое изображение комплексных чисел 11

2.3 Тригонометрическая и показательная формы комплексного

числа 13

Глава 3. Действия с комплексными числами 16

3.1 Сложение комплексных чисел 16

3.2 Вычитание комплексных чисел 17

3.3 Произведение комплексных чисел 17

3.4 Извлечение корней 18

3.5 Геометрический смысл алгебраических операций 19

Глава 4. Применение комплексных чисел к решению

алгебраических уравнений 3-ей и 4-ой степеней 21

4.1 Формула Кардано 21

4.2 Метод Феррари для уравнения 4-ой степени 22

Заключение 23

Список использованных источников 24

Введение
Актуальность

Решение многих задач физики и техники приводит к квадратным уравнениям с отрицательным дискриминантом. Эти уравнения не имеют решения в области действительных чисел. Но решение многих таких задач имеет вполне определенный физический смысл. Значение величин, получающихся в результате решения указанных уравнений, назвали комплексными числами. Комплексные числа широко использовал отец русской авиации Н. Е. Жуковский (1847 – 1921) при разработке теории крыла, автором которой он является.

Цель проектной работы - познакомиться с историей появления комплексных чисел, их свойствами, действиями над ними.

Задачи:

1) Узнать, что такое комплексные числа и для чего они предназначены и как появились.

2) Научиться выполнять разнообразные действия с комплексными числами.

3) Научиться представлять комплексные числа в алгебраической, тригонометрической и показательной формах.

4) Узнать, как строится геометрическая модель комплексного числа.

Объект: История математики.

Предмет: История комплексных чисел.

Гипотеза: В основе работы лежит предположения, что появление комплексных чисел было обусловлено необходимостью решения прикладных задач.

Методы исследования: Работа с Интернет-ресурсами.

Глава 1 История возникновения комплексных чисел

1.1 Развитие понятия о числе

Древнегреческие математики считали “настоящими” только натуральные числа. Постепенно складывалось представление о бесконечности множества натуральных чисел.

В III веке Архимед разработал систему обозначения вплоть до такого громадного как . Наряду с натуральными числами применяли дроби - числа, составленные из целого числа долей единицы. В практических расчетах дроби применялись за две тысячи лет до н. э. в древнем Египте и древнем Вавилоне. Долгое время полагали, что результат измерения всегда выражается или в виде натурального числа, или в виде отношения таких чисел, то есть дроби. Древнегреческий философ и математик Пифагор учил, что «… элементы чисел являются элементами всех вещей и весь мир в целом является гармонией и числом». Сильнейший удар по этому взгляду был нанесен открытием, сделанным одним из пифагорейцев. Он доказал, что диагональ квадрата несоизмерима со стороной. Отсюда следует, что натуральных чисел и дробей недостаточно, для того чтобы выразить длину диагонали квадрата со стороной 1. Есть основание утверждать, что именно с этого открытия начинается эра теоретической математики: открыть существование несоизмеримых величин с помощью опыта, не прибегая к абстрактному рассуждению, было невозможно.

Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел - это было сделано китайскими математиками за два века до н. э. Отрицательные числа применяли в III веке древнегреческий математик Диофант, знавший уже правила действия над ними, а в VII веке эти числа уже подробно изучили индийские ученые, которые сравнивали такие числа с долгом. С помощью отрицательных чисел можно было единым образом описывать изменения величин. Уже в VIII веке было установлено, что квадратный корень из положительного числа имеет два значения - положительное и отрицательное, а из отрицательных чисел квадратный корень извлекать нельзя: нет такого числа , чтобы .

1.2 На пути к комплексным числам
В 1494 году учёный, францисканский монах (Италия) Лука Пачиоло (1445 – 1514) напечатал в Венеции труд “ Сумма, арифметика, геометрия и пропорциональности” , который закончил выводом: “ Решение кубических уравнений вида x³ + px = q, p > 0, q > 0, столь же невозможно при современном состоянии науки, как и решение квадратуры круга циркулем и линейкой” .

Несмотря на это предупреждение, за решение кубического уравнения взялись одновременно сразу два математика, Джеронимо Кардано (1501 – 1576) из Милана и Николо Тарталья (1506 – 1559) из Вероны. Причём первый из них получил аналитический результат, решая квадратное уравнение.

Он поставил задачу: нарезать участок земли прямоугольной формы с площадью 40 кв. ед. и периметром 2р = 20 лин. ед. Решая систему 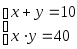, он пришёл к уравнению x² - 10x + 40 = 0, корни которого не являются действительными числами. Он показал, что система уравнений не имеющая решений во множестве действительных чисел, имеет решения вида , . Кардано был удивлён таким результатом, назвав число софистическим, добавив, что “ для осуществления таких действий нужна была бы новая арифметика, которая была бы настолько же утончённой, насколько бесполезной” , нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что . Итальянский алгебраист Дж. Кардано в 1545 г. предложил ввести числа новой природы.

В 1572 году замечательный учёный из Болоньи Рафаэли Бомбелли (1530 – 1572) в своём труде “Алгебра” показывает, что при некоторых операциях над новыми числами результатом является действительное число, например: 1)

2)

3)

Только в XVIII веке величайший математик Леонард Эйлер (1707 – 1783) в работе “Введение в математический анализ” (1746) вводит обозначение мнимой единицы: 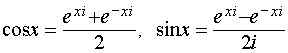, взяв первую букву слова imaginеi res (от названия введённого Р. Декартом (1596 – 1650)) и записывает свои знаменитые формулы: exi = cosx + isinx, e-xi = cosx - isinx, из которых получает соответственно:

Карл Гаусс (1777 – 1855), немецкий учёный, “ король математики” , впервые называет числа комплексными (от латинского c o m p l e k s – объединение), вводит обозначение а + bi и представляет их в виде точек плоскости.

В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. В формуле для решения кубических уравнений вида кубические и квадратные корни: .

Эта формула безотказно действует в случае, когда уравнение имеет один действительный корень ( x=1), а если оно имеет три действительных корня ( x₁=1 x_2,3 = ), то под знаком квадратного корня оказывалось отрицательное число. Получалось, что путь к этим корням ведет через невозможную операцию извлечения квадратного корня из отрицательного числа. Вслед за тем, как были решены уравнения 4-й степени, математики усиленно искали формулу для решения уравнения 5-й степени. Но Руффини (Италия) на рубеже XVIII и XIX веков доказал, что буквенное уравнение пятой степени нельзя решить алгебраически; точнее: нельзя выразить его корень через буквенные величины a, b, c, d, e с помощью шести алгебраических действий (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня).

В 1830 году Галуа (Франция) доказал, что никакое общее уравнение, степень которого больше чем 4, нельзя решить алгебраически. Тем не менее, всякое уравнение n-й степени имеет (если рассматривать и комплексные числа) n корней (среди которых могут быть и равные). В этом математики были убеждены еще в XVII веке (основываясь на разборе многочисленных частных случаев), но лишь на рубеже XVIII и XIX веков упомянутая теорема была доказана Гауссом.

1.3 Утверждение комплексных чисел в математике

Кардано называл такие величины “чисто отрицательными” и даже “софистически отрицательными”, считал их бесполезными и старался их не употреблять. В самом деле, с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение какой-нибудь величины. Но уже в 1572 году вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Название “мнимые числа” ввел в 1637 году французский математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII века - Л. Эйлер предложил использовать первую букву французского слова imaginaire(мнимый) для обозначения числа (мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу. Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д., образующих единое целое.

В течение XVII века продолжалось обсуждение арифметической природы мнимых чисел, возможности дать им геометрическое обоснование.

Постепенно развивалась техника операций над мнимыми числами. На рубеже XVII и XVIII веков была построена общая теория корней n-ых степеней сначала из отрицательных, а за тем из любых комплексных чисел, основанная на следующей формуле английского математика А. Муавр (1707): . С помощью этой формулы можно было так же вывести формулы для косинусов и синусов кратных дуг. Л. Эйлер вывел в 1748 году замечательную формулу: , которая связывала воедино показательную функцию с тригонометрической. С помощью формулы Л. Эйлера можно было возводить число e в любую комплексную степень. Любопытно, например, что . Можно находить sin и cos от комплексных чисел, вычислять логарифмы таких чисел, то есть строить теорию функций комплексного переменного.

В конце XVIII века французский математик Ж. Лагранж смог сказать, что математический анализ уже не затрудняют мнимые величины. С помощью мнимых чисел научились выражать решения линейных дифференциальных уравнений с постоянными коэффициентами. Такие уравнения встречаются, например, в теории колебаний материальной точки в сопротивляющейся среде. Еще раньше швейцарский математик Я. Бернулли применял комплексные числа для решения интегралов.

Хотя в течение XVIII века с помощью комплексных чисел были решены многие вопросы, в том числе и прикладные задачи, связанные с картографией, гидродинамикой и т. д., однако еще не было строго логического обоснования теории этих чисел. Поэтому французский ученый П. Лаплас считал, что результаты, полученные с помощью мнимых чисел, - только наведение, приобретающее характер настоящих истин лишь после подтверждения прямыми доказательствами.

“Никто ведь не сомневается в точности результатов, получаемых при вычислениях с мнимыми количествами, хотя они представляют собой только алгебраические формы иероглифы нелепых количеств” Л. Карно.

После создания теории комплексных чисел возник вопрос о существовании “гиперкомплексных” чисел - чисел с несколькими “мнимыми” единицами. Такую систему вида , где , построил в 1843 году ирландский математик У. Гамильтон, который назвал их “кватернионами”. Правила действия над кватернионами напоминает правила обычной алгебры, однако их умножение не обладает свойством коммутативности (переместительности): например, , а .

Большой вклад в развитие теории функций комплексного переменного внесли русские и советские ученые Н. И. Мусхелишвили занимался ее применениями к упругости, М. В. Келдыш и М. А. Лаврентьев - к аэро- и гидродинамике, Н. Н. Богомолов и В. С. Владимиров - к проблемам квантовой теории поля.

Глава 2 Комплексные числа и их свойства

2.1 О комплексных числах
В связи с развитием алгебры потребовалось ввести сверх прежде известных положительных и отрицательных чисел числа нового рода. Они называются комплексными. Комплексное число имеет вид a + bi; здесь a и b – действительные числа , а i – число нового рода, называемое мнимой единицей. “Мнимые” числа составляют частный вид комплексных чисел (когда а = 0). С другой стороны, и действительные числа являются частным видом комплексных чисел (когда b = 0).

Действительное число a назовем абсциссой комплексного числа a + bi; действительное число b – ординатой комплексного числа a + bi. Основное свойство числа i состоит в том, что произведение i×i равно –1, т.е.

i²= -1. (1)

Долгое время не удавалось найти такие физические величины, над которыми можно выполнять действия, подчинённые тем же правилам, что и действия над комплексными числами – в частности правилу (1). Отсюда названия: “мнимая единица”, “мнимое число” и т.п. В настоящее время известен целый ряд таких физических величин, и комплексные числа широко применяются не только в математике, но также и в физике и технике.

Правило каждого действия над комплексными числами выводится из определения этого действия. Но определения действий над комплексными числами не вымышлены произвольно, а установлены с таким расчетом, чтобы согласовались с правилами действий над вещественными числами. Ведь комплексные числа должны рассматриваться не в отрыве от действительных, а совместно с ними.

Действительное число а записывается также в виде a + 0i (или a – 0i).

Примеры. Запись 3 + 0i обозначает то же, что запись 3. Запись –2 + 0i означает –2.

Комплексное число вида 0 + bi называется “чисто мнимым”. Запись bi обозначает то же, что 0 + bi. Два комплексных a + bi, a’ + b’i считаются равными, если у них соответственно равны абсциссы и ординаты, т. е. если a = a’, b = b’. В противном случае комплексные числа не равны. Это определение подсказывается следующим соображением. Если бы могло существовать, скажем, такое равенство: 2 + 5i = 8 + 2i, то по правилам алгебры мы имели бы i = 2, тогда как i не должно бать действительным числом.
2.2 Геометрическое изображение комплексных чисел
Действительные числа можно изобразить точками прямой линии, как показано на рис.1, где точка С изображает число 4. Это число можно изобразить также отрезком ОС, учитывая не только его длину, но и направление.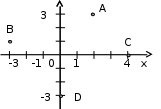


Рисунок 1 – Геометрическое изображение действительных чисел
Каждая точка С “числовой прямой” изображает некоторое действительное число (рациональное, если отрезок ОС соизмерим с единицей длины, и иррациональное, если несоизмерим). Таким образом, на “числовой прямой” не остаётся места для комплексных чисел.

Но комплексные числа можно изобразить на “числовой прямой”. Для этого мы выбираем на плоскости прямоугольную систему координат с одним и тем же масштабом на обеих осях (рис. 2). Комплексное число a + bi мы изображаем точкой, у которой абсцисса х равна абсциссе а комплексного, а ордината у равна ординате b комплексного числа .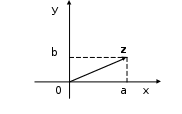



Рисунок 2 – Геометрическое представление комплексного числа
Комплексное число может также изображаться вектором с координатами a и b, идущим из начала координат в точку (a; b). По определению модуля комплексного числа

, (2)

модуль комплексного числа равен длине вектора .

Пример. На рис. 1 точка А с абсциссой х=2 и ординатой у=3 изображает комплексное число 2+3i. Точка В (-3,-1) изображает комплексное число: –3 - i.

Действительные числа (в комплексной форме они имеют вид a + 0i) изображают точками оси OХ, а чисто мнимые – точками оси OУ.

Пример. Точка С на рис. 1 изображает действительное число 4, точка D – чисто мнимое число 3i. Начало координат изображает число 0.

Сопряжённые комплексные числа изображаются парой точек, симметричных относительно оси абсцисс.

Комплексные можно изображать также отрезками, начинающимися в точке О и оканчивающимися в соответствующей точке числовой плоскости. Так, комплексное число a + bi можно изобразить не только точкой Z (рис. 1), но также вектором ОZ . Давая какому – либо отрезку наименование “вектор”, мы подчёркиваем, что существенное значение имеет не только длина, но и направление отрезка.

Геометрическое истолкование комплексных чисел позволило определить многие понятия, связанные с функцией комплексного переменного, расширило область их применения.

Стало ясно, что комплексные числа полезны во многих вопросах, где имеют дело с величинами, которые изображаются векторами на плоскости: при изучении течения жидкости, задач теории упругости.

2.3 Тригонометрическая и показательная формы комплексного числа
Понятия «больше» или «меньше» для комплексных чисел лишено смысла (не принято никакого соглашения).

Если на плоскости введена декартова система координат 0xy, то всякому комплексному числу z=x+iy может быть поставлена в соответствие некоторая точка М (х, у) с абсциссой «х» и ординатой «у», а также радиус – вектор 0М. При этом говорят, что точка М (х, у) (или радиус – вектор 0М) изображает комплексное число z=x+iy.

Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, ось 0у – мнимой осью.

Число r=√x²+y²­, равное длине вектора, изображающего комплексное число, т.е. расстоянию от начала координат до изображающей это число точки, называется модулем комплексного числа z=x+iy и обозначается символом |z|.

Угол φ=(0М, 0х) между положительным направлением оси 0х и вектором 0М, изображающим комплексное число z=x+iy ≠0, называется его аргументом.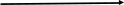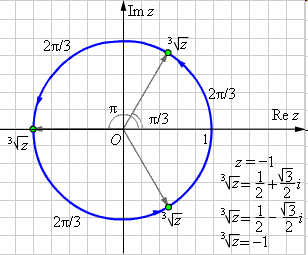



Рисунок 3 –Тригонометрическая форма комплексного числа
Из определения видно, что каждое комплексное число (≠0), имеет бесконечное множество аргументов. Все они отличаются друг от друга на целые кратные 2π и обозначаются единым символом Argz (для числа z=0 аргумент не определяется, не имеет смысла).

Каждое значение аргумента совпадает с величиной φ некоторого угла, на который следует повернуть действительную ось (ось 0х) до совпадения ее направления с направлением радиус-вектора точки М, изображающей число z (при этом φ > 0, если поворот совершается против часовой стрелки и φ <0 в противном случае). Таким образом, аргумент комплексного числа z=x+iy ≠0 есть всякое решение φ системы уравнений cosφ=x/√x²+y²; sinφ=y/√x²+y².

Значение Argz при условии 0≤Argz<2π называется главным значением аргумента и обозначается символом argz. В некоторых случаях главным значением аргумента считают наименьшее по абсолютной величине его значения, т.е. значение, выделяемое неравенством -π<φ≤π.

Между алгебраическими х, у и геометрическими r, φ характеристиками комплексного числа существует связь, выражаемая формулами x=rcosφ, y=rsinφ, следовательно, z=x+iy=r(cosφ+isinφ). Последнее выражение, т.е.

z=r(cosφ+isinφ) (3)

называется тригонометрической формой комплексного числа. Любое число z≠0 может быть представлено в тригонометрической форме.

Для практики число вида (cosφ+isinφ) удобнее записывать короче, с помощью символа

e^iφ=cosφ+isinφ (4)

Доказанное для любых чисел φ (действительных или комплексных) это равенство называется формулой Эйлера. С ее помощью всякое комплексное число может быть записано в показательной форме

z=re^iφ (5)
Глава 3 Действия с комплексными числами
3.1 Сложение комплексных чисел
Суммой двух комплексных чисел z₁ = a + bi и z₂ = c + di называется комплексное число z = (a+c) + (b+d)i .

Числа (a + bi) и (a – bi) называются сопряженными. Их сумма равна действительному числу 2а: (а+bi) + (а-bi) = 2а.

Числа (а+bi) и (-a – bi) называются противоположными. Их сумма равна нулю.

Комплексные числа равны, если равны их действительные части и коэффициенты мнимых частей: а+bi = c+di, если a = c, b = d.

Комплексное число равно нулю тогда, когда его действительная часть и коэффициент мнимой части равны нулю, т.е. z = a + bi = 0, если a = 0,b = 0.

Действительные числа являются частным случаем комплексных чисел. Если b = 0, то a + bi = a - действительное число.

Если а = 0, b 0, то a + bi = bi – чисто мнимое число.

Для комплексных чисел справедливы переместительный и сочетательный законы сложения. Их справедливость следует из того, что сложение комплексных чисел по существу сводится к сложению действительных частей и коэффициентов мнимых частей, а они являются действительными числами, для которых справедливы указанные законы.

Пример 1. (-3 + 5i) + (4 – 8i) = 1 - 3i

Пример 2. (2 + 0i) + (7 + 0i) = 9 + 0i. Так как запись 2 + 0i означает то же, что и 2 и т. д., то наполненное действие согласуется с обычной арифметикой (2 + 7=9).

Пример 3. (0 + 2i) + (0 + 5i) = 0 + 7i, т. е. 2i + 5i = 7i

Пример 4. (-2 + 3i) + ( - 2 – 3i) = - 4
3.2 Вычитание комплексных чисел
Вычитание комплексных чисел определяется как действие, обратное сложению: разностью двух комплексных чисел a + bi и с + di называется комплексное число х + уi, которое в сумме с вычитаемым дает уменьшаемое. Отсюда, исходя из определения сложения и равенства комплексных чисел, получим два уравнения, из которых найдем, что х = а-с, у = b-d. Значит, (а+bi) - (c+di) = (a-c) + (b-d)i.

Пример 1. (-5 + 2i) – (3 – 5i) = -8 + 7i

Пример 2. (3 + 2i) – (-3 + 2i) = 6 + 0i = 6
3.3 Произведение комплексных чисел
z ₁= a + bi * z₂ = c + di называется комплексное число z = (ac-bd) + (ad + bc)i, z₁z₂ = (a + bi)(c + di) = (ac - bd) + (ad + bc)i.

Легко проверить, что умножение комплексных чиcел можно выполнять как умножение многочленов с заменой i² на –1. Для умножения комплексных чисел также справедливы переместительный и сочетательный законы, а также распределительный закон умножения по отношению к сложению.

Из определения умножения получим, что произведение сопряженных комплексных чисел равно действительному числу: (a + bi)(a - bi) = a² + b²

Деление комплексных чисел, кроме деления на нуль, определяется как действие, обратное умножению. Конкретное правило деления получим, записав частное в виде дроби и умножив числитель и знаменатель этой дроби на число, сопряженное со знаменателем:

(a + bi):(c + di) = = = + i. (6)

Степень числа i является периодической функцией показателя с периодом 4. Действительно,

i² = -1, i³ = -i, i⁴ = 1, i⁴ⁿ = (i⁴)ⁿ = 1ⁿ = 1, i⁴ⁿ⁺¹ = i, i⁴ⁿ⁺² = -1, i⁴ⁿ⁺³ = -i.

Пример 1. (1 – 2i)(3 + 2i) = 3 – 6i + 2i – 4i ^{2 ­} = 3 – 6i + 2i + 4 = 7 – 4i.

Пример 2. (a + bi)(a – bi) = a² + b ²

Пример 3. Найти частное (7 – 4i):(3 + 2i).

Записав дробь (7 – 4i)/(3 + 2i), расширяем её на число 3 – 2i, сопряженное с 3 + 2i. Получим:

((7 – 4i)(3 - 2i))/((3 + 2i)(3 – 2i)) = (13 – 26i)/13 = 1 – 2i.

Пример 2 показывает, что произведение сопряженных комплексных чисел есть действительное и притом положительное число.

Для умножения комплексных чисел также справедливы переместительный и сочетательный законы, а также распределительный закон умножения по отношению к сложению.
3.4 Извлечение корней
Извлечение корня из комплексного числа есть действие, обратное возведению в степень. С его помощью по данной степени (подкоренное число) и данному показателю степени (показатель корня) находят основание (корень). Иначе говоря, это действие равносильно решению уравнения zⁿ=a для нахождения z. В множестве комплексных чисел действие извлечения корня всегда выполнимо, хотя причем и неоднозначно: в результате получается столько значений, каков показатель корня. В частности, квадратный корень имеет ровно два значения, которые можно найти по формуле:

√a=√α+iβ=±((√|a|+α)/2 ± i(√|a|-α)/2)), (7)

где знак «+» в скобках берется при β>0, «-» - при β<0.

3.5 Геометрический смысл алгебраических операций
Пусть даны два комплексных числа z₁ и z₂. В результате сложения этих чисел получается число z₃, изображаемое вектором 0С диагонали параллелограмма 0АСВ (по правилу параллелограмма сложения векторов): z₁+z₂=0A+0B=0C=z₃.

Разность (z₁-z₂) данных чисел, соответствующая их вычитанию, можно рассматривать как сумму вектора 0А, изображающего число z₁ и вектора 0D=--0В, противоположного вектору 0В (симметричного ему относительно начала координат): z₁-z₂=z₁+(-z₂)=0A+0D=0E=BA. Таким образом, разности (z₁-z₂) данных чисел соответствует вектор ВА другой диагонали параллелограмма 0АСВ (рис.4).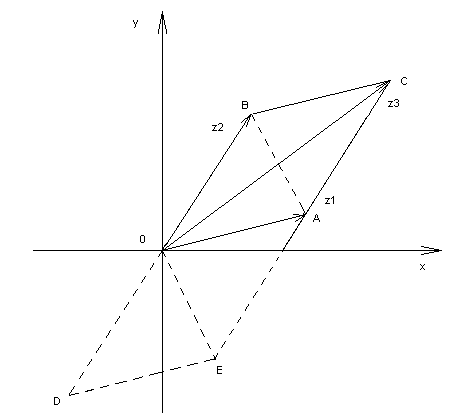



Рисунок 4 – Геометрический смысл суммы и разности комплексных чисел
Для иллюстрации остальных алгебраических действий над комплексными числами более удобна тригонометрическая форма.

Умножение. Пусть даны два комплексных числа z₁=r₁(cosφ₁+isinφ₁) и z₂=r₂(cosφ₂+isinφ₂). Перемножая их получим z₁z₂=r₁r₂(cos(φ₁+φ₂)+isin(φ₁+φ₂)). Следовательно, при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Это правило верно и для любого числа сомножителей.

Деление. Если требуется разделить z₁ на z₂, то выполняем следующие преобразования: z₁/z₂=(z₁z₂)/(z₂z₂)=(r₁(cosφ₁+isinφ₁)r₂(cosφ₂-isinφ₂))/ (r₂(cosφ₂+isinφ₂)r₂(cosφ₂-isinφ₂))=(r₁/r₂)(cos(φ₁-φ₂)+isin(φ₁-φ₂)), т.е. при делении двух комплексных чисел их модули делятся, а аргументы вычитаются.

Возведение в степень. Умножая число z=r(cosφ+isinφ) само на себя «n» раз, получаем согласно правилу умножения zⁿ=rⁿ(cosφ+isinφ)ⁿ=rⁿ(cosnφ+isinnφ). Таким образом, при возведении комплексного числа в степень «n» в ту же степень возводится его модуль, а аргумент умножается на «n» (на показатель степени). В частном случае, если Извлечение корня. Пусть а=re^iφ, z=ρe^iσ. Решаем уравнение zⁿ=a для вычисления ⁿ√a: ρⁿe^inσ=re^iφ. Отсюда с учетом того, что аргументы чисел отличаются на целое кратное числу 2π, получаем: ρⁿ=r, nσ-φ=2πK, или ρ=ⁿ√r; σ_K+1=(φ+2πK)/n (причем К=0,1,2…n-1). Таким образом, z_k=ⁿ√r(cosφ+isinφ)=ⁿ√r((cosφ+2Kπ)/n+isin(φ+2Kπ)/n)), (8)

где ⁿ√r , - арифметический корень, а К=0,1,2,…,n-1; т.е. корень степени n в множестве комплексных чисел имеет “n” различных значений z_k (исключение представляет z=0. В этом случае все значения корня равны между собой и равны нулю).

Заметим также, что разность между аргументами соседних чисел z_k+1 и z_k постоянна и равна 2π/n: σ_k+1-σ_k=(φ+2π(K+1))/n-(φ+2πK)/n=2π/n. Отсюда следует, что все значения ⁿ√a располагаются на комплексной плоскости в вершинах некоторого правильного n-угольника с центром в начале координат.

Глава 4 Применение комплексных чисел к решению алгебраических уравнений 3-ей и 4-ой степеней
4.1 Формула Кардано
Рассмотрим приведенное алгебраическое уравнение 3-ей степени:

x³+ax²+bx+c=0 (9).

(общее уравнение 3-ей степени сводится к приведенному делением на коэффициент при старшей степени). С помощью замены x=y-a/3 это уравнение примет вид:

y³+py+q=0, (10)

где p и q – новые коэффициенты, зависящие от a,b,c.

Пусть у₀ – какой либо корень уравнения (10). Представим его в виде у₀=α+β, где α и β – неизвестные пока числа, и подставим в уравнение. Получим α³+β³+( α+β)(3αβ+p)+q=0 (11)

Выберем теперь α и β так, чтобы 3αβ+р=0. Такой выбор чисел α и β возможен, т.к. они (вообще говоря комплексные) удовлетворяют системе уравнений

α+β=у₀;

αβ=-р/3, а значит, существуют.

П ри этих условиях уравнение (10) примет вид α³+β³+q=0, а т.к. еще α³β³=-р³/27, то получаем систему

α³+β³=-q;

α³β³=-р³/27,

из которой по теореме Виета следует, что α³ и β³ являются корнями уравнения t²+qt-p³/27=0. Отсюда находим: α³=-q/2+√q²/4+p³/27; β³=-q/2-√q²/4+p³/27, где √q²/4+p³/27 означает одно из возможных значений квадратного корня. Отсюда следует, что корни уравнения (9) выражаются формулой D=(q/2)²+(p/3)³.

y_1.2.3=ⁿ√-q/2+√q²/4+p³/27+³√-q/2-√q²/4+p³/27, причем для каждого из трех значение первого корня ³√α соответствующие значения второго корня ³√β нужно брать так, чтобы было выполнено условие αβ=-р/3. Полученная формула называется формулой Кардано (ее можно записать в более компактном виде у=³√α+³√β, где α=-q/2+√q²/4+p³/27; β=-q/2-√q²/4+p³/27. Подставив в нее вместо р и q их выражения через a,b,c и вычитая а/3, получим формулу для уравнения (10).
4.2 Метод Феррари для уравнения 4-ой степени
Рассмотрим приведенное уравнение 4-ой степени

x⁴+ax³+bx²+cx+d=0 (12)

Сделав замену переменной х=у-а/4, получим уравнение

у⁴+ру²+qy+r=0 (13)

c коэффициентами p,q,r, зависящими от a,b,c,d. Преобразуем это уравнение к виду (y²+p/2)²+qy+(r-p²/4)=0, а затем, введя произвольное пока число α, представим его левую часть в равносильной форме (y²+p/2+α)²-[2α(y²+p/2)+α²-qy+p²/4-r]=0 (14)

Выберем теперь число α так, чтобы выражение в квадратных скобках 2αy²-qy+(αp+α²+p²/4-r) стало полным (точным) квадратом относительно у. Для этого нужно, чтобы его дискриминант был равен нулю, т.е. чтобы q²-8α(αp+α²+p²/4-r)=0, или 8α³+8pα²+8α(p²/4-r)-q²=0. Таким образом, для нахождения α получается уравнение 3-ей степени, и задача сводится к предыдущей. Если в качестве «α» взять один из корней этого уравнения, то левая часть уравнения (13) будет разностью квадратов и поэтому может быть разложена в произведение двух многочленов 2-ой степени относительно «у».

Заключение
Комплексные числа, несмотря на их “лживость” и недействительность, имеют очень широкое применение. Они играют значительную роль не только в математике, а также в таких науках, как физика, химия. В настоящее время комплексные числа активно используются в электромеханике, компьютерной и космической индустрии. Именно поэтому необходимо расширять свои знания о комплексных числах, их свойствах и особенностях.

В настоящем проекте дано понятие комплексных чисел, история их возникновения. Рассмотрены примеры действий с комплексными числами. Приведены примеры решения уравнений с комплексным переменным, что позволяет решить любые квадратные уравнения, даже с отрицательным дискриминантом.

Также рассмотрена геометрическая интерпретация комплексных чисел в виде векторов.

Список использованных источников

1. 
   Андронов, И.К. Математика действительных и комплексных чисел: учебное пособие / И.К. Андронов. – Москва: Просвещение, 2018.- 158с. - Текст: непосредственный.
   
2. 
   Гордиенко, Н.А. Комплексные числа и их приложения: учебное пособие / Н.А. Гордиенко, Э.С. Беляева, В.Е. Фирстов, И.В. Серебрякова.– Воронеж: ВГПУ (университет), 2018.- 92 с.- Текст: непосредственный.
   

3.Курош, А.Г. Алгебраические уравнения произвольных степеней» учебное пособие / А.Г. Курош.- Москва: Наука, 2017.- 32 с.- Текст: непосредственный.

4. Маркушевич, А.И. Комплексные числа и конформные отображения: учебное пособие / А.И. Маркушевич.- Москва: Физматгиз, 2019.- 56 с.- Текст: непосредственный.

5. Стройк, Д.Я. Краткий очерк истории математики: учебное пособие / Д.Я. Стройк.- Москва: Наука, 2019.- 284 с.- Текст: непосредственный.

6. Яглом, И.М. Комплексные числа и их приложения в геометрии: учебное пособие / И.М. Яглом.- Москва: Едиториал УРСС, 2018.- 192 с.- Текст: непосредственный.

7. Комплексное число.- Текст: электронный // Википедия – свободная энциклопедия : сайт. - 2004. – URL : https://ru.wikipedia. org/wiki/Комплексное_число (дата обращения 26.03.2021)