РЕФЕРАТ НА ТЕМУ МЕТОДОВ ЛИНЕЙНОГО ПРОГРАМИРОВАНИЕ. История развития линейного программирования

• Название: История развития линейного программирования
• Дата: 02.01.2019
• Размер: 199.96 Kb.
• Имя файла: РЕФЕРАТ НА ТЕМУ МЕТОДОВ ЛИНЕЙНОГО ПРОГРАМИРОВАНИЕ.docx
• Тип: Документы; #62299
• страница: 4 из 5

Метод потенциалов

Метод потенциалов является модификацией симплекс-метода решения задачи линейного программирования применительно к транспортной задаче. Он позволяет, отправляясь от некоторого допустимого решения, получить оптимальное решение за конечное число итераций.

Двойственные переменные симплекс-метода для транспортной задачи называются потенциалами.

Таким образом, потенциал потребителя равен потенциалу производителя + стоимость перевозки. С экономической точки зрения это можно трактовать как стоимость продукта в точке потребления.

Добавление дуги приводит к возникновению цикла в дереве. Увеличение провоза по вводимой дуге приводит к пересчету потоков в цикле, провоз по одной из дуг при этом уменьшится до нуля. Дугу с нулевым потоком удаляем из базиса, при этом базисный граф остаётся деревом (цикл разрывается).

Обычно в постановке сумма производства больше суммы потребления. Для решения незамкнутых задач, а также для простоты получения начального базисного плана используется метод искусственного базиса [4]. Для этого исходный граф расширяется, вводится «свалка» — дополнительный пункт, на который свозится все лишнее производство за нулевую цену.

Если ввести дуги со свалки в пункты потребления с очень высокой ценой, начальное решение строится тривиально — все производство везем на свалку, все потребление — со свалки.

Дуги на свалку от пунктов производства соответствуют дополнительным переменным в симплекс-методе, а дуги со свалки к пунктам потребления соответствуют искусственным переменным.

Для матричной транспортной задачи возможен другой алгоритм построения начального плана.

2. Выберем дугу, инцидентную i. Поток по дуге положим равным минимуму из объёмов производства и потребления на концах дуги. Уменьшим эти объёмы на величину потока по дуге. Вершину с нулевым объёмом устраним из рассмотрения вместе с инцидентными ей дугами. Переходим к пункту 2.

Если вершины производств и потребления перенумерованы и каждый раз выбирается дуга с наименьшим номером, метод называется методом северо-западного угла [5].

Определение выводимой дуги и пересчет потенциалов достаточно эффективно реализуется. Основным «потребителем» времени становится проверка оптимальности.

Для уменьшения времени на проверку оптимальности применяется несколько приемов.

1. Использование барьера — как только величина невязки больше некоторой величины, дугу вводим в базис, не перебирая остальные дуги. Если дуга не найдена, уменьшаем барьер до максимальной найденной невязки и соответствующую дугу вводим в базис.

2. Циклический просмотр — перебор начинается с того места, на котором остановились в предыдущем просмотре.

3. Выбор «претендентов» — при просмотре выбирается не одна дуга, а несколько. На следующем шаге проверяются только отобранные дуги.

Определитель базисной матрицы всегда равен 1, так что при целочисленных данных задача дает целочисленные решения.

Алгоритм очень похож на стандартный метод потенциалов. Насыщенная дуга должна не удовлетворять критерию оптимальности, в противном случае поток по ней следует уменьшать. Остальные дуги проверяются на критерий так же, как и в стандартном варианте. Так же, как и в стандартном алгоритме, в обоих случаях появляется контур, в котором следует изменять поток (уменьшать для выбранной дуги в случае вывода дуги из насыщенных и увеличивать в случае обычной дуги). При изменении потоков одна из дуг может выйти на 0 (как в стандартном алгоритме) или на верхнюю границу пропускной способности — переводим её в насыщенные.

http://dir.md/wiki/Метод_потенциалов?host=ru.wikipedia.org

Метод Мак-Кормака

Метод Мак-Кормака – это конечно-разностный метод типа предиктор-корректор. Метод Мак-Кормака широко используется для решения задач движения сжимаемого потока и других задач последние 30 лет. С момента появления схема Ма-Кормака претерпела множество модификаций и обобщений. Существуют как явная, так и неявная версии этого алгоритма. Также развита модификация для применения в методе конечных объемов. Метод Мак-Кормака считается краеугольным камнем вычислительной гидродинамики. Как явная, так и неявная версии метода позволяют решать гиперболические и параболические уравнения для положительного временного шага, при этом проявляя хорошие диссипативные и дисперсионные краевые свойства.

Популярность явного метода Мак-Кормака обусловлена как простотой его выражений, так и простотой применения этого метода, в том числе и для многомерных задач. Этапы предиктора и корректора используют прямое дифференцирование для производных по времени первого порядка, и одностороннее дифференцирование пространственной производной первого порядка. (Bernard., 1992) Для предиктора и корректора при дифференцировании по времени используется только разности «вперед». А вот направления пространственного дифференцирования в предикторе и корректоре всегда противоположны. В примере, если в схеме на шаге предиктор используются разности «назад», то в корректоре – «вперед». Разности «назад» и «вперед» можно циклически чередовать: таким образом, устраняется рассогласование, обусловленное аппроксимацией односторонними разностями, благодаря чему при вычислении нет нужды в расчете Якобиана, как это происходит в одно-шаговой явной схеме типа Лакса-Вендроффа.

http://mylektsii.ru/9-118641.html

Метод Т. Мака

Метод работает в предположении, что для оценки резерва убытков к имеющемуся треугольнику развития применим метод цепной лестницы. Иными словами, предполагается, что фактический треугольник является некоторым случайным возмущением «правильного» треугольника развития, все столбцы которого пропорциональны друг другу. Коэффициенты пропорциональности в соответствии со сложившейся терминологией, называются факторами развития. В своей работе Мак предлагает три способа выбора факторов развития:

– средневзвешенный по всем периодам (классический метод CLM);

– среднеарифметический;

– среднеквадратичный.

Также допускается при расчете средних использовать произвольные веса, чтобы снизить влияние отдельных всплесков в индивидуальных факторах развития (или вовсе исключить их).

Для каждого из способов выбора факторов развития (в т.ч. и с весами) Мак в явном виде выводит формулу оценки дисперсии (среднеквадратичного отклонения) для величины резерва убытков, полученной с помощью CLM. Математическим ожиданием резерва убытков будет являться резерв, вычисленный по методу CLM.

Сам по себе метод Мака не дает никакой информации о функции распределения резерва убытков, оцениваются только параметры данного распределения. В качестве рекомендаций предлагается считать, что резерв убытков имеет нормальное или логнормальное распределение. Логнормальное более предпочтительно, т.к. по определению не может принимать отрицательных значений (как и резерв убытков). 

http://www.actuaries.ru/magazine/detail.php?ID=4874
Симплекс-метод.

Симплекс-метод является классическим и наиболее проработанным методом в линейном программировании. Он позволяет за конечное число шагов либо найти оптимальное решение, либо установить, что оптимальное решение отсутствует.

Сформулирован алгоритм решения задачи, который проиллюстрирован на примере.

Основное содержание симплексного метода заключается в следующем:

1. 
   Указать способ нахождения оптимального опорного решения
   
2. 
   Указать способ перехода от одного опорного решения к другому, на котором значение целевой функции будет ближе к оптимальному, т.е. указать способ улучшения опорного решения
   
3. 
   Задать критерии, которые позволяют своевременно прекратить перебор опорных решений на оптимальном решении или следать заключение об отсутствии оптимального решения.
   

2. Симплексный метод решения задач линейного программирования

Симплексный метод решения задач линейного программирования (симплекс-метод) - вычислительная процедура, основанная на принципе последовательного улучшения решений — перехода от одной базисной точки к другой, для которой значение целевой функции больше (эти операции фиксируются в симплексной таблице).

Данный метод является методом целенаправленного перебора опорных решений задачи линейного программирования. Он позволяет за конечное число шагов либо найти оптимальное решение, либо установить, что оптимальное решение отсутствует. Доказано, что если оптимальное решение существует, то оно обязательно будет найдено через конечное число шагов (за исключением т.н. вырожденной задачи, при которой возможно явление «зацикливания», т.е. многократного возврата к одному и тому же положению).

Симплекс-метод является основным в линейном программировании. Решение задачи начинается с рассмотрений одной из вершин многогранника условий. Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к соседней, увеличивая значение функции цели при решении задачи на максимум и уменьшая при решении задачи на минимум. Таким образом, переход от одной вершины к другой улучшает значение функции цели. Так как число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима.

Этот метод является универсальным, применимым к любой задаче линейного программирования в канонической форме. Система ограничений здесь - система линейных уравнений, в которой количество неизвестных больше количества уравнений. Если ранг системы равен r, то мы можем выбрать r неизвестных, которые выразим через остальные неизвестные. Для определенности предположим, что выбраны первые, идущие подряд, неизвестные X1, X2, ..., Xr. Тогда наша система уравнений может быть записана как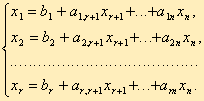



К такому виду можно привести любую совместную систему, например, методом Гаусса. Правда, не всегда можно выражать через остальные первые r неизвестных (мы это сделали для определенности записи). Однако такие r неизвестных обязательно найдутся. Эти неизвестные (переменные) называются базисными, остальные свободными.

Придавая определенные значения свободным переменным и вычисляя значения базисных (выраженных через свободные), мы будем получать различные решения нашей системы ограничений. Таким образом, можно получить любое ее решение. Нас будут интересовать особые решения, получаемые в случае, когда свободные переменные равны нулю. Такие решения называются базисными, их столько же, сколько различных базисных видов у данной системы ограничений. Базисное решение называется допустимым базисным решением или опорным решением, если в нем значения переменных неотрицательны. Если в качестве базисных взяты переменные X1, X2, ..., Xr, то решение {b1, b2,..., br, 0, ..., 0} будет опорным при условии, что b1, b2,..., br ≥ 0.

Симплекс-метод основан на теореме, которая называется фундаментальной теоремой симплекс-метода. Среди оптимальных планов задачи линейного программирования в канонической форме обязательно есть опорное решение ее системы ограничений. Если оптимальный план задачи единственен, то он совпадает с некоторым опорным решением. Различных опорных решений системы ограничений конечное число. Поэтому решение задачи в канонической форме можно было бы искать перебором опорных решений и выбором среди них того, для которого значение F самое большое. Но, во-первых, все опорные решения неизвестны и их нужно находить, a, во-вторых, в реальных задачах этих решений очень много и прямой перебор вряд ли возможен. Симплекс-метод представляет собой некоторую процедуру направленного перебора опорных решений. Исходя из некоторого, найденного заранее опорного решения по определенному алгоритму симплекс-метода мы подсчитываем новое опорное решение, на котором значение целевой функции F не меньше, чем на старом. После ряда шагов мы приходим к опорному решению, которое является оптимальным планом.

Итак, симплексный метод вносит определенный порядок как при нахождении первого (исходного) базисного решения, так и при переходе к другим базисным решениям.

Реализация решения задачи симплекс-методом наглядно показана на блок-схеме (рис.1).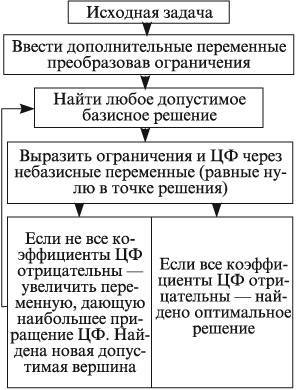



Таким образом, применение симплексного метода распадается на два этапа: нахождение допустимого базисного решения системы ограничений или установление факта ее несовместности; нахождение оптимального решения. При этом каждый этап может включать несколько шагов, соответствующих тому или иному базисному решению. Но так как число базисных решений всегда ограниченно, то ограниченно и число шагов симплексного метода.

Приведенная схема симплексного метода явно выражает его алгоритмический характер (характер четкого предписания о выполнении последовательных операций), что позволяет успешно программировать и реализовать этот метод на ЭВМ. Задачи же с небольшим числом переменных и ограничений могут быть решены симплексным методом вручную.

Опишем его вычислительную сторону. Вычисления по симплекс-методу организуются в виде симплекс-таблиц, которые являются сокращенной записью задачи линейного программирования в канонической форме. Перед составлением симплекс-таблицы задача должна быть преобразована, система ограничений приведена к допустимому базисному виду, c помощью которого из целевой функции должны быть исключены базисные переменные. Вопрос об этих предварительных преобразованиях мы рассмотрим ниже. Сейчас же будем считать, что они уже выполнены и задача имеет вид: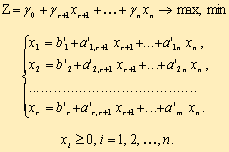



Здесь для определенности записи считается, что в качестве базисных переменных можно взять переменные X1, X2, ..., Xr и что при этом b1, b2,..., br ≥ 0 (соответствующее базисное решение является опорным).

Для составления симплекс-таблицы во всех равенствах в условии задачи члены, содержащие переменные, переносятся в левую часть, свободные оставляются справа, т.е. задача записывается в виде системы равенств: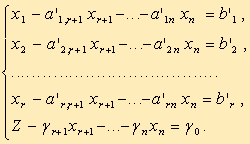



Далее эта система оформляется в виде симплекс-таблиц: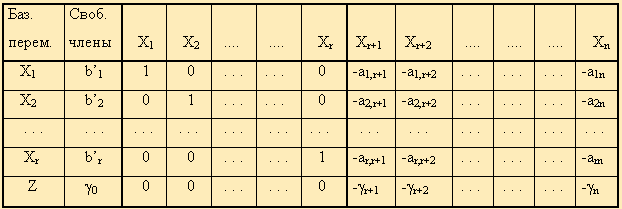



Примечание. Названия базисных переменных здесь взяты лишь для определенности записи и в реальной таблице могут оказаться другими.

Порядок работы с симплекс таблицей. Первая симплекс-таблица подвергается преобразованию, суть которого заключается в переходе к новому опорному решению.

Алгоритм перехода к следующей таблице такой:

просматривается последняя строка (индексная) таблицы и среди коэффициентов этой строки (исключая столбец свободных членов) выбирается наименьшее отрицательное число при отыскании max, либо наибольшее положительное при задачи на min. Если такового нет, то исходное базисное решение является оптимальным и данная таблица является последней;

просматривается столбец таблицы, отвечающий выбранному отрицательному (положительному) коэффициенту в последней строке- ключевой столбец, и в этом столбце выбираются положительные коэффициенты. Если таковых нет, то целевая функция неограниченна на области допустимых значений переменных и задача решений не имеет;

среди выбранных коэффициентов столбца выбирается тот, для которого абсолютная величина отношения соответствующего свободного члена (находящегося в столбце свободных членов) к этому элементу минимальна. Этот коэффициент называется разрешающим, а строка в которой он находится ключевой;

в дальнейшем базисная переменная, отвечающая строке разрешающего элемента, должна быть переведена в разряд свободных, а свободная переменная, отвечающая столбцу разрешающего элемента, вводится в число базисных. Строится новая таблица, содержащая новые названия базисных переменных:

разделим каждый элемент ключевой строки (исключая столбец свободных членов) на разрешающий элемент и полученные значения запишем в строку с измененной базисной переменной новой симплекс таблицы;

строка разрешающего элемента делится на этот элемент и полученная строка записывается в новую таблицу на то же место;

в новой таблице все элементы ключевого столбца = 0, кроме разрезающего, он всегда равен 1;

столбец, у которого в ключевой строке имеется 0,в новой таблице будет таким же;

строка, у которой в ключевом столбце имеется 0,в новой таблице будет такой же;

в остальные клетки новой таблицы записывается результат преобразования элементов старой таблицы: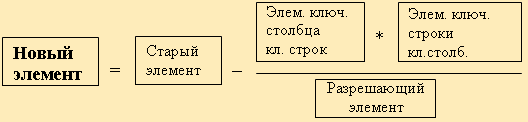



В результате получают новую симплекс-таблицу, отвечающую новому базисному решению. Теперь следует просмотреть строку целевой функции (индексную), если в ней нет отрицательных значений (в задачи на нахождение максимального значения), либо положительных (в задачи на нахождение минимального значения) кроме стоящего на месте (свободного столбца), то значит, что оптимальное решение получено. В противном случае, переходим к новой симплекс таблице по выше описанному алгоритму.

https://works.doklad.ru/view/wgdsLOdeEoM.html

Методы поиска решений в пространстве (графах) состояний.

Методы перебора. Решение многих задач в интеллектуальных системах можно определить как проблему поиска, где искомое решение – это цель поиска, а множество возможных путей достижения цели представляет собой пространство поиска (или пространство состояний). Поиск решений в пространстве состоит в определении последовательности операторов, которые преобразуют начальное состояние в целевое.

Задачу поиска в пространстве состояний можно сформулировать в общем виде так: Пусть исходная задача описывается тройкой (S, F, T), где S – множество начальных состояний; F – множество операторов, отображающих одни состояния в другие; T – множество целевых состояний. Решение задачи состоит в нахождении последовательности операторов f₁,f₂,…,f_k (f_i ÎF), которые преобразуют начальные состояния в конечные. Задача поиска в пространстве состояний описывается с помощью понятий теории графов [41]. Задается начальная вершина (исходное состояние) и множество целевых вершин T. Для построения пространства состояний используются операторы F. Последовательно от корня к вершинам дерева применяются операторы, относящиеся к этому уровню, для построения вершин-преемников следующего уровня (раскрытие вершин). Дуги идентифицируются как операторы преобразования. Получаемые вершины - преемники проверяются: не являются ли они целевыми. Далее переходят к следующему уровню. Терминальные вершины – это те, к которым нельзя применить никаких операторов. Раскрытие продолжается до тех пор, пока не получена целевая или терминальная вершина. Поиск на графе состояний – это процесс построения графа G, содержащего целевую вершину. Этот граф называется графом поиска. Различие нескольких вариантов реализации метода перебора, которые отличаются заданным порядком, в котором будут перебираться вершины.

Поиск в глубину. При поиске в глубину прежде всего раскрывается та вершина, которая имеет наибольшую глубину. Из вершин, расположенных на одинаковой глубине, выбор вершины для раскрытия определяется произвольно. Для сдерживания возможности следования по бес пути вводится ограничение на глубину. Вершины, находящиеся на граничной глубине, не раскрываются.

Поиск в ширину. Вершины раскрываются в последовательности их порождения. Поиск идет по ширине дерева, т. к. раскрытие вершины происходит вдоль одного уровня. Целевая вершина выбирается сразу же после порождения. При поиске в ширину возможно нахождение наиболее короткого пути к целевой вершине, если такой путь есть. На рис. 6.3 представлены графы поиска, построение при поиске в глубину и в ширину.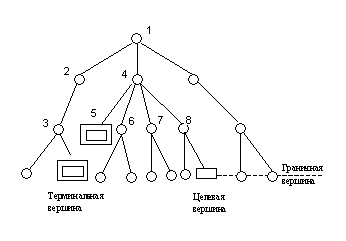



а)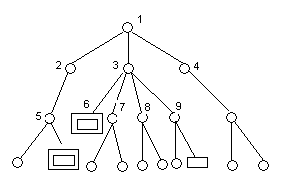



б)