РЕФЕРАТ НА ТЕМУ МЕТОДОВ ЛИНЕЙНОГО ПРОГРАМИРОВАНИЕ. История развития линейного программирования

• Название: История развития линейного программирования
• Дата: 02.01.2019
• Размер: 199.96 Kb.
• Имя файла: РЕФЕРАТ НА ТЕМУ МЕТОДОВ ЛИНЕЙНОГО ПРОГРАМИРОВАНИЕ.docx
• Тип: Документы; #62299
• страница: 5 из 5

Рис. 6.3. Графы поиска, построенные при поиске в глубину (а) и ширину (б)

Поиск на основе стоимости дуг.Во многих случаях дугам ставят в соответствие некоторую стоимость, чтобы внести оценку для использования соответствующего правила. При поиске целевой вершины стремятся найти путь минимальной стоимости. Раскрытие вершин производится в порядке возрастания их стоимости. Для каждой вершины нужно помнить минимальную стоимость пути, построенного от начальной вершины до нее.

Поиск с возвратом (бэктрекинг).При реализации такого поиска при выборе правила определяется точка возврата, т. е. если дальнейший поиск в выбранном направлении приведет к сложностям или будет бесперспективным, то осуществляется переход к точке возврата, пройденной на ранних этапах поиска. Далее применяется другое правило, и процесс поиска продолжается. Здесь все неудачные итерации, приведшие к тупиковой ситуации, забываются, как только применяется новое правило, и переходят к другому направлению поиска. Такой метод поиска с возвратом называется хронологическим возвратом. Он часто малоэффективен, т. к. не запоминает неудачные состояния и шаги поиска, встретившиеся на некотором пути. Многие из них впоследствии окажут свое отрицательное влияние при реализации других путей. Т. о. много полезной информации отбрасывается и не используется при анализе дальнейших направлений поиска. Необходимо анализировать шаги вывода, приведшие к тупиковым ситуациям и ошибкам. Для этого надо запоминать шаги вывода. Кроме того, возвращаться надо не к точке возврата, предшествующей данному состоянию, а к состоянию, которое вызвало неудачный ход поиска.

Для методов поиска решения при представлении пространства состояний в виде графа характерно то, что в них в основном предусматривается запоминание результатовприменения нескольких последовательностей правил. Другая особенность – они работают в пробном режиме, т. е. при выборе и использовании применимого правила для какой-либо ситуации предусматривается возможность возврата к этой ситуации для применения другого правила. Достоинствами методов перебора является достаточно простая их реализация и возможность в принципе находить решение, если оно существует. Однако на практике всегда есть ограничения по времени и объему памяти на процесс реализации поиска. Для больших пространств и сложных массивов задач методы перебора неприемлемы – реальность комбинаторного взрыва. Для сокращения поиска необходима информация, называемая эвристической.

Эвристические методы поиска.Эти методы поиска возможно использовать тогда, когда располагают некоторыми эмпирическими правилами, которые позволяют сокращать объем просматриваемых вариантов решений. Эвристическая информация основывается на опыте, здравом смысле, допущениях разработчика.

При использовании эвристических методов поиска открытые вершины стремятся упорядочить таким образом, чтобы процесс поиска распространился в наиболее перспективных направлениях. Для определения направления поиска используется некоторая мера, характеризующая перспективность вершины или пути, где эта вершина находится. Эту меру называют оценочной функцией f(n). Эта функция является оценкой стоимости кратчайшего пути из начальной вершины в целевую при условии, что он проходит через вершину n. При раскрытии вершины или определении пути выбирается вершина с минимальным значением оценочной функции. Оценочная функция должна адекватно характеризовать пространство поиска, т.е. необходим достаточно большой объем знаний о проблемной области и тщательный анализ пространства состояний. На практике использование количественных характеристик и весовых коэффициентов для представления этих знаний себя не оправдывает, так как применение не позволяет эффективно вести поиск решений (могут потребоваться большие объемы вычислений). Кроме того, эвристический поиск с использование оценочной функции предполагает достоверное знание пространства состояний. Однако в реальной практике при принятии решений сталкиваются с фактами и знаниями недостаточно полными и определенными. Кроме того, часто на процесс поиска влияет дефицит времени. В этих условиях люди используют методы, отличные от формального математического рассуждения. Формальное математическое рассуждение является монотонным, т.е. каждое заключение следует из предыдущего. (Монотонность – свойство некоторых логических и математических операций (функций), которое, говоря обобщенно, состоит в том, что направление возможного изменения результата операций зависит только от направления изменения того, над чем эти операции производятся.)

Специалисты, принимающие решения, используют немонотонные рассуждения, или рассуждения здравого смысла (основывающиеся на общих элементарных знаниях). Несмотря на то, что рассуждения здравого смысла являются довольно обыденными для людей, очень трудно достигнуть требуемого уровня реализации подобных рассуждений в ИИ. (Тем не менее, в некоторых классических ЭС, таких как MYCIN, PROSPECTOR, этот метод довольно успешно реализован для сокращения пространства поиска.

При рассуждениях здравого смысла процедура поиска строится на некоторых предположениях при отсутствии информации, противоречащей этим предположениям. Предположения могут изменяться при поступлении дополнительной проясняющей информации, т.е. в системах поиска, основывающихся на предположениях, необходим просмотр предположений о характере ситуации и направлении поиска при получении новых фактов и знаний Необходим также пересмотр выводов, полученных на основании этих предположений. (Совмещение с процедурами возврата)

Метод редукции. Поиск необходимой совокупности данных для решения задачи сводится к решению составляющих подзадач. Задачи описываются различными способами: списки, деревья, массивы. Рассмотрим форму описания задачи как поиск в пространстве состояний. В данном представлении подзадачи рассматриваются как задачи нахождения связи определенными состояниями в пространстве поиска. Для представления исходной задачи в виде совокупности подзадач используется оператор перехода к новому описанию. Этот оператор преобразует исходную задачу таким образом, что при решении всех подзадач – преемников обеспечивается решение исходной задачи. Для каждого представления исходной задачи может существовать некоторое множество таких операторов, каждый из которых порождает свою совокупность подзадач. Часть этих подзадач может оказаться неразрешимой. Для других подзадач процесс повторяется, т.е. их в свою очередь, также сводят к подзадачам. Это продолжается до тех пор, пока каждая подзадача не будет иметь очевидное решение.

Процесс преобразования также удобно описывать с помощью графовых структур. Процесс поиска решения исходной задачи при таком описании представляет собой направленный граф редукции задач. Этот граф называется графом И/ИЛИ. Вершины этого графа представляют описания задач и подзадач. Граф И/ИЛИ содержит вершины двух типов. Тип “И” – соответствует задаче, решаемой при условии реализации всех ее подзадач в соответствующих вершинах – преемниках. Тип “ИЛИ” – соответствует задаче, решение которой возможно получить при решении одной из альтернативных подзадач в соответствующих вершинах – преемниках. На рис. 6.4. представлены фрогменты графов типа И/ИЛИ.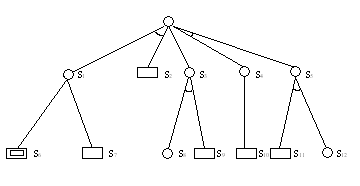



a)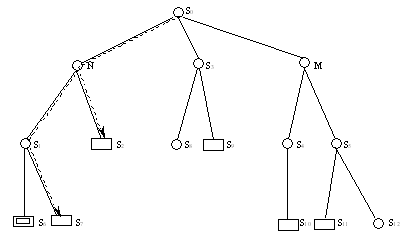



б)

Рис. 6.4. Представление разбиения исходной задачи на подзадачи в виде графа И/ИЛИ (а) и преобразование графа И/ИЛИ (б).

Исходная задача S₀ разбивается на группы подзадач. Она может быть решена путем решения подзадач либо S₁ и S₂; либо S₃; S₄ и S₅. Вершины N, S₃, M, S₅ – это вершины типа “И”. Штриховой линией показан вариант решающего графа исходной задачи. Решения подзадач S₂, S₇, S₉, S₁₀, S₁₁ - предполагают известными. Решения других подзадач неизвестны. В структуру обычно вводятся дополнительные вершины, чтобы каждое множество подзадач формировалось под своей собственной родительской вершиной. Вершина графа И/ИЛИ может принадлежать к типу И либо ИЛИ. Поэтому исходный граф преобразуется и вводятся дополнительные вершины N и M, которые служат отдельными родительскими вершинами для подзадач {S₁, S₂} и {S₄, S₅. Таким образом, вершина S₀ преобразуется в вершину ИЛИ.

Реализация графа редукции аналогична реализации графа поиска решений в пространстве состояний. В частном случае, если вершин И нет, получается обычный граф пространства состояний. Поэтому метод редукции является в какой-то степени обобщением подхода с использованием пространства состояний.

Существуют различные методы организации поиска и вывода решений в больших пространствах состояний. Применение того или иного метода связано с характером пространства состояний, его структурируемостью, возможность описания области решений на различных уровнях абстракции, возможностью оценки перспективных путей поиска и другими факторами.

Реальная проблемная область характеризуется зачастую настолько большим пространством состояний, что бывает очень трудно практически организовать поиск методами перебора. Однако часто требуется найти все возможные решения в проблемной области. Выходом в таких случаях является использование метода порождения и проверки. Этот метод можно применять, если пространство является факторизуемым, т. е. возможно разбиение его на достаточно независимые подпространства с характерными неполными решениями. Характерное неполное решение позволяет судить о перспективности поиска полных решений в этом подпространстве.

Сущность метода заключается в том, что генератор, настроенный на проблемную область, порождает ряд характерных неполных решений, соответствующих описаниям различных подпространств. Осуществляется проверка неполных решений с помощью специальных оценочных процедур, и если решение признается недопустимым, то из дальнейшего рассмотрения исключается целый класс порождаемых им полных решений данного подпространства. В результате отсечения на ранней стадии поиска определенных ветвей поиска без порождения и проверки узлов состояний значительно сокращается число состояний, подлежащих анализу. Если неполное решение признается перспективным, то на его основе в соответствующем подпространстве вырабатываются полные решения на более глубоких уровнях иерархии описания пространства и определяется, являются ли получаемые решения целевыми.

Иерархическая процедура реализации метода порождения и проверки позволяет применять правила отсечения вариантов на ранних этапах порождения. Использование метода порождения и проверки в факторизованном пространстве бывает затруднено из-за того, что часто отсутствуют достоверные способы оценки характерных неполных решений, т. е. не удается на основе неполных решений делать выводы о реализуемости полных решений. Здесь невозможно с большой степенью уверенности отсечь неперспективные ветви на начальной стадии поиска. Всегда есть риск исключить часть пространства состояний, представившегося бесперспективным, но вполне способным в дальнейшей обработке при появлении дополнительной информации обеспечить решение. Такие ситуации характерны для задач перспективного планирования и проектирования. Кроме того, не всегда необходимо искать все возможные решения, а достаточно иметь какое-либо приемлемое.

В этих случаях производят абстрагирование пространства решений. Решение задачи осуществляется на разных уровнях абстракции путем последовательного уточнения его на этих уровнях описания пространства. Абстракция дополнительно выявляет важные детали, характеризующие задачу. Основная задача редуцируется на фиксированную совокупность описаний подзадач. В простых случаях в абстрактном пространстве достаточно одного разбиения, используемого для разных задач данной проблемной области.

Если проблемная область содержит большое число задач, то не удается все задачи решить на определенном варианте редукции пространства поиска. В качестве примера можно привести задачу планирования действий робота по перемещению в пространстве и манипулированию объектами. В этих случаях абстракция должна отразить переменную структуру плана действий.

Возможно использование метода последовательного уточнениясверху. Этот метод характеризуется тем, что создает абстракцию, адекватную каждой задаче. Причем для упрощения процесса решения задачи сначала получают обобщенное описание пространства и решают задачу в этом пространстве, а затем переходят к более конкретному описанию пространства. Таким образом, решение задачи реализуется сверху вниз, от поиска и определения решения в абстрактном пространстве к преобразованию этого решения и его конкретизации на более низких (т. е. более подробных) уровнях описания. Переход к более конкретному уровню осуществляется лишь после завершения решения на рассматриваемом уровне абстракции.

При поиске решений в больших пространствах состояний используются также эвристические методы и процедуры. Часто трудно выделить чисто эвристическую процедуру, так как она бывает в большей или меньшей степени встроена в какой-либо из названных методов. Например, эвристические оценки присутствуют в методе порождения я проверки, когда генератор строит гипотезы относительно характерных неполных решений, которые затем проверяются. При использовании метода последовательного уточнения сверху предполагается и допускается, что решение задачи на верхних уровнях абстракции позволит конкретизировать решение на более подробных уровнях описания задачи.

Необходимость формулирования гипотез при поиске решений может быть вызвана многими причинами: невозможностью сделать выбор направления поиска на определенном этапе решения при реализации какого-либо метода, недостаточностью фактов и знаний; нехваткой времени для проработки различных вариантов решений; ограниченностью других ресурсов. В этих случаях выдвигается разумная гипотеза о дальнейшем направлении поиска, которая остается действующей до тех пор, пока на основе новой информации, получаемой при решении, не становится очевидным противное. Практически стремятся реализовать рассуждения при предположении здравого смысла, т. е. немонотонные рассуждения, что довольно не просто в практических системах ИИ, о чем говорилось выше.

Трудности связаны прежде всего с этапом формирования разумной гипотезы, а кроме того, с возможностью пересмотра сделанных предположений при получении новых знаний и фактов, выводимых при решении задачи или поступающих в систему извне. Таким образом, главная проблема — выявление .неверных гипотез и реализация способов отказа от таких гипотез в ходе правдоподобных рассуждений.

Выше были рассмотрены лишь основные методы поиска в больших пространствах. При практической реализации систем ИИ возможно появление новых методов поиска решений и построения рассуждений, часто ориентированных на определенные классы реальных проблемных областей с учетом их специфики.

https://studopedia.ru/18_40603_obshchie-metodi-poiska-resheniy-v-prostranstve-sostoyaniy.html