перевод иностранный. готово 5 стр исправл. Итерационный метод с управляемой мощностью отклика для локализации высокоточных акустических источников (Л)
 Скачать 155.58 Kb. Скачать 155.58 Kb.
|
|
Итерационный метод с управляемой мощностью отклика для локализации высокоточных акустических источников (Л) Ампаро Мартия a) Институт iTEAM, Политехнический университетская Валенсии, 46022, Валенсия, Испания Максимо Кобос Факультет компьютерных технологий, Университет Валенсии, 46100, Буржасот, Валенсия, Испания Хосе Ж. Лопес Факультет коммуникаций, Политехнический университетская Валенсии, 46022, Валенсия, Испания Хосе Эсколано Исследования Sophandrey, Улица Западная 13, Бруклин, Нью-Йорк 11223 (Получено 24 мая 2013 г., пересмотрено 8 августа 2013 г. , принято 14 августа 2013 г.) Локализация источника с использованием управляемой мощности отклика (SRP) обычно требует дорогостоящей процедуры сетевого поиска. Для решения этой проблемы недавно был модифицирован алгоритм SRP, обеспечивающий повышенную устойчивость при использовании более грубых пространственных сеток. В этом документе представлен итерационный метод, основанный на модифицированном SRP. Первоначально грубая пространственная сетка оценивается с помощью модифицированного SRP, выбирая точку с самым высоким накопленным значением. Затем соответствующий его объем повторно разлагается с помощью более тонкой пространственной сетки. Эксперименты показали, что этот метод обеспечивает почти такую же точность, как и мелкосерийный поиск с существенным снижением функциональных оценок. © 2013 Акустическое общество Америки. [Http://dx.doi.org/10.1121/1.4820885] Номер PACS: 43.60.Jn [SAF] Страницы: 2627-2630 I. ВВЕДЕНИЕ В последние десятилетия локализация источников звука привлекает большое внимание. Микрофонные системы известны своими многочисленными приложениями, такими как видеонаблюдение, телеконференции, улучшение речи для слуховых аппаратов или системы наведения камеры 1. _________________ a)Автор, которому адресовано письмо. Электронная почта: ammargue@iteam.upv.es Большинство этих приложений требуют, чтобы локальное значение обладало высокой точностью и разумными вычислительными затратами, особенно в режиме реального времени2. (SRP) с алгоритмом фазового преобразования считается одним из самых надежных алгоритмов локализации в реверберирующих средах3. Однако, вычислительные затраты значительно выше преимуществ. В этом контексте было предложено несколько модификаций и оптимизаций для улучшения его производительности и применимости. Недавно авторы предложили модифицированную версию алгоритма, для улучшения производительности локализации, приспособив функциональные оценки SRP к масштабируемым размерам сетки4. Однако, несмотря на то, что вычислительные затраты были значительно уменьшены, окончательная точность в конце определяется выбранным пространственным разрешением. В этом документе мы предлагаем расширенную стратегию, основанную на итерационной процедуре декомпозиции сетки для улучшения модифицированного алгоритма SRP. Метод оценивается в различных акустических условиях и сравнивается с другими алгоритмами на основе SRP. II. МОДИФИЦИРОВАННЫЙ SRP АЛГОРИТМ Рассмотрим выходной сигнал от микрофона l, ml (t) в системе M-микрофона. Алгоритм SRP основан на вычислении обобщенной взаимной корреляции (GCC) 5 (с фазовым преобразованием) между парами микрофонов (k,l), заданной формулой  (1) (1) где τ - время запаздывания, * обозначает комплексное сопряжение, а Ml(ω) - преобразование Фурье сигнала микрофона ml(t). SRP в пространственной точке x=[x,y,z] T для временной рамки n длины T может быть выражена как 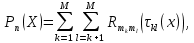 (2) (2) где 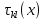 - функция задержки времени между микрофонами. Эта функция представляет собой теоретическую задержку времени поступления для пары микрофонов (k,l), полученную от точечного источника, расположенного в точке x. Это дается выражением - функция задержки времени между микрофонами. Эта функция представляет собой теоретическую задержку времени поступления для пары микрофонов (k,l), полученную от точечного источника, расположенного в точке x. Это дается выражением 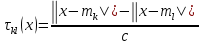 (3) (3)где c - скорость звука (в этой работе использовалось 340 м/с), а mk и ml - соответствующие местоположения микрофона. Для реализации алгоритма пространство обычно дискретизируется с помощью пространственной сетки G с пространственным разрешением r, так что уравнение (2) учитывает только значение GCC в дискретном пространстве x G. Заметим, что имеется всего Q=M(M-1)/2 пары микрофонов, которые должны обрабатываться. Предполагается, что местоположение источника во временном диапазоне n таково, что максимизируется Pn(x). Становится очевидным, что при использовании грубой пространственной сетки, скорее всего, будет не хватать глобального максимума пространства SRP. Для решения этой проблемы модифицированный SRP основан на накоплении запаздывания GCC, соответствующего объему, окружающему каждую точку пространственной сетки, в результате чего  (4) Пределы накопления GCC 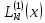 и и 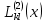 определяются градиентом функции задержки между микрофонами, соответствующим каждой паре микрофонов, таким образом, что принимается во внимание пространственное распределение возможных временных разностей, возникающих в результате данном расположении массива. Компоненты градиента определяются градиентом функции задержки между микрофонами, соответствующим каждой паре микрофонов, таким образом, что принимается во внимание пространственное распределение возможных временных разностей, возникающих в результате данном расположении массива. Компоненты градиента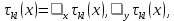  задаются выражением задаются выражением 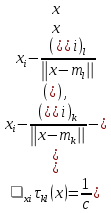 (5) Пределы накопления в зависимости от компонентов градиента равны  (6) (6) 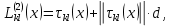 (7) (7)где для кубической пространственной сетки 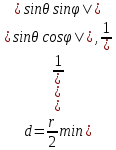 (8) (8) составляет угол наклона градиента 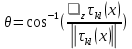 и азимутальный угол и азимутальный угол . Наконец, вычисленное местоположение источника xs заключается в максимизации модифицированного функционала по заданной пространственной сетке, то есть . Наконец, вычисленное местоположение источника xs заключается в максимизации модифицированного функционала по заданной пространственной сетке, то есть  (9) (9)III. ПРЕДЛАГАЕМЫЙ ПОДХОД A. Основанный на функциональных возможностях Подход, предложенный в этой статье, использует модифицированный функционал SRP с дополнительной вариацией. Вместо суммирования всех значений GCC между вычисленными пределами, мы вычисляем среднее по этому интервалу следующим образом:  (10) Средний функционал в уравнении (10) предназначен для компенсации накопленного GCC, рассматрвиаемого эти значения в результате очень больших интервалов, избегая при этом больших функциональных значений из-за накопленного шума. Чтобы проиллюстрировать эту идею, рассмотрим пример на рис. 1(a), который показывает градиент функции задержки для установки с двумя микрофонами по грубой пространственной сетке.  РИС1. (Цвет онлайн) A и B охватывают различные интервалы накопления в грубой сетке. (а) Градиент функции задержки. (а) Шумная GCC. Линии представляют полугиперболы с постоянной задержкой. Заметим, что заштрихованные области A и B охватывают различное количество линий с постоянной задержкой, что приводит к различным интервалам накопления. На рисунке 1(b) показан шумный GCC, полученный из той же самой установки и соответствующих диапазонов суммирования для A и B с частотой дискретизации 44,1 кГц. Обратите внимание, что, несмотря на то, что A содержит пик прямого звука GCC, накопленное значение в B может быть больше из-за накопления шума в течение большего интервала. Предлагаемый функционал, основанный на среднем, смягчает этот нежелательный эффект. Следует подчеркнуть, что, в отличие от узкополосных методов, эффекты пространственного наложения спектров широкополосных микрофонных массивов на основе SRP не так важны6. В нашем случае, несмотря на то, что для исключения пространственного наложения не применяется специальная обработка, сигналы микрофона фильтруются для поддерживания только составляющих сигналов в диапазоне частот речи. B. Итерационные разложение объема Шаги алгоритма, выполняемые в каждом временном диапазоне n, следующие: (1) Вычисление GCC с использованием сигналов входного микрофона во временном диапазоне n. Начинается с итерации i=0 и начального пространства локализации V-1=Vtotal. (2) Определение пространственного разрешения ri и построение пространственной сетки Gi, покрывающей желаемое пространство локализации Vi-1. (3) Применение уравнения (10) ко всем точкам сетки x Gi и выбор точки с наибольшим значением  (4) Новое пространство локализации заключается в том, что покрытие всех пространственных точек ближе к xi, чем любая другая точка сетки, то есть Vi ={x| ||x-xi|| ≤ || x- x Gi ||, x Gi ≠ xi }. (5) Переход к шагу (2) с итерацией i=i+1 и увеличение пространственного разрешения ri  РИС 2. Процедура деления субдома. C. Вычислительные затраты Предполагая, что лимиты накопления 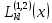 предварительно вычислены в процессе инициализации, вычислительные затраты предлагаемого метода отличаются от обычных SRP только по общему числу требуемых функциональных оценок νm. Если разрешение на каждой итерации определяется как постоянное масштабирование предыдущего решения, ri=α ri-1, с α<1, тогда предварительно вычислены в процессе инициализации, вычислительные затраты предлагаемого метода отличаются от обычных SRP только по общему числу требуемых функциональных оценок νm. Если разрешение на каждой итерации определяется как постоянное масштабирование предыдущего решения, ri=α ri-1, с α<1, тогда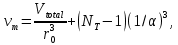 (11) (11)приводя к окончательному решению rf = r0· αNT-1. Следовательно, соотношение между числом операций обычного SRP, имеющего окончательное разрешение rf (обозначаемое как νf), и предлагаемое значение составляют 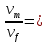 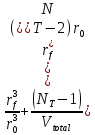 (12) (12) Если NT≤3, то уравнение (12) можно аппроксимировать выражением (rf/r0) 3. На рисунке 3(a) показано вышеприведенное соотношение для трехмерной сетки с разными начальными значениями r0 и rf=0,01 м. На рис. 3(b) показаны возможные комбинации α и NT для тех же начальных разрешений, что и на рис. 3 (а). IV. ЭКСПЕРИМЕНТЫ На рис. 3 (а) показано, что сокращение вычислкеий сильно зависит от выбранного начального разрешения r0. Разделы IVA-IVD оценивают эффективность предлагаемого подхода с различными исходными разрешениями и сравнивают его с другими подходами на основе SRP.  РИС3. (a) Редукция для различных начальных разрешений r0 и rf=0,01м. (b) Комбинации a и NT. Проведение оценки акустической модели на основе источника изображения7 было выполнено путем рассмотрения прямоугольного помещения с размерами 4м х 6м х 3м с переменным коэффициентом отражения на стенке ρ и отношением сигнал/шум (SNR). С этой целью был применен пакет Roomsim MATLAB8. В качестве источника звука использовался речевой сигнал длительностью 5 с, и результаты всегда представлялись путем усреднения 56 различных точек источников, равномерно распределенных на плоскости. Объем поиска был ограничен двумерной сеткой в одной плоскости. Для избежания неречевых кадров, источник звука был сегментирован вручную, чтобы включать только речевые кадры в вычисленные результаты. Система локализации состояла из M=6 микрофонов, расположенных в углах комнаты и в середине самой длинной стены. Обработка была выполнена с использованием частоты дискретизации 44,1 кГц, с временными окнами длиной 4096 выборок и 50% перекрытием. Параметр α всегда выбирался так, чтобы обеспечить окончательное разрешение rf=0,01 м после NT =3 итераций. A. Влияние начального разрешения На рисунках 4 (a) и 4(b) показана среднеквадратическая ошибка (RMSE) для различных начальных разрешений r0 в зависимости от SNR и коэффициента отражения стенки ρ соответственно. Также представлено соответствующее время реверберации T60 (в сек). На рис. 4 (a), ρ зафиксировано до 0,5, тогда как на рис. 4(b), SNR фиксировано до 25 дБ. Исходные испытанные разрешения те же, что и показанные на рис. 3. Обратите внимание, что при адекватных акустических условиях (SNR≤20 дБ и ρ≤0,5) RMSE всегда меньше rf (RMSE≈ 0,0035 м), независимо от r0. Различия между разными начальными разрешениями больше, когда SNR уменьшается и/или увеличивается реверберация (более высокое ρ). Это связано с тем, что более грубые решетки стремятся интегрировать больше шумов и ложных пиков GCC в неблагоприятных условиях, приводя к ошибкам в первой итерации. Однако относительная производительность среди различных начальных разрешений существенно не отличается при умеренных акустических условиях. В результате грубая начальная пространственная сетка (r0=0,5 м) позволяет проводить высокоточную локализацию, обеспечивая при этом уменьшение функциональных оценок на 105 при использовании трехмерного сетевого поиска. B. Сравнение алгоритмов В этом разделе сравниваются характеристики предложенного метода с двумя другими алгоритмами локализации: сжатие грубо-тонкой области (CFRC) 9 и обычный алгоритм SRP (Conv). Предлагаемый метод оценивается для NT=3, rf=0,01м и r0=0,5 м. 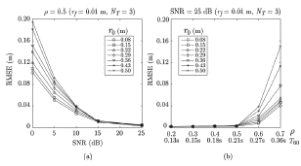 РИС4. (a) RMSE по отношению к SNR для q¼ 0,5. (B) RMSE против q для SNR = 25 дБ. 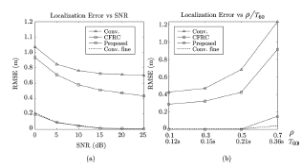 РИС5. Сравнение алгоритмов. (A) RMSE по отношению к SNR для q = 0,5. (B) RMSE против q для SNR = 25 дБ. РИС5. Сравнение алгоритмов. (A) RMSE по отношению к SNR для q = 0,5. (B) RMSE против q для SNR = 25 дБ.Обычный SRP оценивается для сетки, имеющей разрешение r=0,35 м, тогда как CFRC оценивается с использованием предложенных параметров9 (точек сетки J=300 и выбранных точек N=100). Кроме того, производительность алгоритма SRP с мелкой сеткой с разрешением r=0,01 м (Conv. Fine) также представляется в качестве образца. Эксперименты проводились в MATLAB с использованием портативного компьютера с двухъядерным процессором 1,7 ГГц и 4 ГБ оперативной памяти. Число функциональных оценок и среднее время вычисления tc для каждого случая: 196 для обычного SRP и предложенного алгоритма (tc=44 мс), 900 для CFRC (tc=46 мс) и 240,000 для мелкосеточного SRP (tc=920 мс). На рисунках 5(a) и 5(b) показаны результаты изменения SNR и коэффициента отражения соответственно. Обратите внимание, что предложенный метод явно превосходит остальные при использовании сопоставимого числа функциональных оценок. Фактически, производительность обычного SRP с r=0,01 м и предложенным методом очень схожи, с RMSE, который стремится аппроксимировать окончательное разрешение, когда акустические условия благоприятны. C. Реальная настройка. Реальная комната с размерами 5,7х6,7х2,1 м и T60=0,28 мс была взята для проверки применимости метода в реальных условиях. Схема микрофона была очень похожа на ту, что использовалась в симуляциях, и параметры алгоритма были такими же, как в разд. IV B. Таблица 1 содержит полученный RMSE для сравниваемых алгоритмов, показывающий, что предложенный метод имеет ту же производительность, что и метод мелкосеточной SRP. D. Обсуждение Обратите внимание, что как предложенный метод, так и CFRC основаны на итерационном сжатии исходного объема поиска, пока не будет достигнут достаточно малый объем. Однако в CFRC функционал, оцененный по каждой пространственной точке, соответствует функциональному признаку обычного SRP. В результате объем, окружающий каждую точку исходной сетки, не учитывается алгоритмом, что увеличивает вероятность сбоя на первом шаге, когда число начальных точек J недостаточно велико. ТАБЛИЦА1. RMSE для реаольной установки
Более того, операция сокращения в CFRC выполняется путем определения новой области (подобъема), содержащей лучшие N точек (с более высоким функциональным значением). В нашем методе достаточно выбрать только самый лучший, что значительно упрощает операцию сжатия и заставляет алгоритм быстрее сходиться к желаемому конечному разрешению. V. ЗАКЛЮЧЕНИЕ В этом документе представлен итерационный подход для высокоточной локализации источника звука с использованием модифицированного функционала SRP. Метод начинается с выполнения локализации источника по очень грубой пространственной сетке. Затем область сетки, имеющей самое высокое накопленное значение, делится на более мелкие области до достижения желаемого пространственного разрешения. Проведен ряд экспериментов по оценке этого нового подхода, сравнение его точности локализации с другими хорошо известными подходами в различных акустических условиях. Результаты показывают, что предложенный метод имеет производительность, сопоставимую с эффективностью мелкосеточного SRP с уменьшением приблизительно на 5 порядков по функциональным оценкам. ВЫРАЖЕНИЕ ПРИЗНАТЕЛЬНОСТИ Министерство экономики и конкурентоспособности Испании и FEDER поддержали эту работу в рамках проектов TEC2012-37945-C02-01 / 02. 1A. Y. Nakano, S. Nakagawa, and K. Yamamoto, “Automatic estimation of position and orientation of an acoustic source by a microphone array network,” J. Acoust. Soc. Am. 126, 3084–3094 (2009). 2M. Durkovic´, T. Habigt, M. Rothbucher, and K. Diepold, “Low latency localization of multiple sound sources in reverberant environments,” J. Acoust. Soc. Am. 130, 392–398 (2011). 3J. H. DiBiase, “A high accuracy, low-latency technique for talker localization in reverberant environments using microphone arrays,” Ph.D. thesis, Brown University, Providence, RI (2000). 4M. Cobos, A. Marti, and J. J. Lopez, “A modified SRP-PHAT functional for robust real-time sound source localization with scalable spatial sampling,” IEEE Signal Process. Lett. 18, 71–74 (2011). 5C. H. Knapp and G. C. Carter, “The generalized correlation method for estimation of time delay,” IEEE Trans. Acoust., Speech, Signal Process. ASSP-24, 320–327 (1976). 6J. Dmochowski, J. Benesty, and S. Affes, “On spatial aliasing in microphone arrays,” IEEE Trans. Signal Process. 57, 1383–1395 (2009). 7J. B. Allen and D. A. Berkley, “Image method for efficiently simulating small-room acoustics,” J. Acoust. Soc. Am. 65, 943–950 (1979). 8D. R. Campbell, “Roomsim: A MATLAB simulation shoebox room acoustics,” (2007) [Online]. Available: http://media.paisley.ac.uk/campbell/Roomsim (Last viewed July 30, 2013). 9H. Do and H. F. Silverman, “A fast microphone array SRP-PHAT source location implementation using coarse-to-fine region contraction (CFRC),” in Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (New Paltz, NY, 2007). |
