итоговое по высшей математике. Решение итогового задания по высшей математике.. Итоговое задание по высшей математике(Агафонова Н. В.) Задание

• Название: Итоговое задание по высшей математике(Агафонова Н. В.) Задание
• Анкор: итоговое по высшей математике
• Дата: 14.09.2022
• Размер: 36.23 Kb.
• Имя файла: Решение итогового задания по высшей математике..docx
• Тип: Документы; #676697

Итоговое задание по высшей математике(Агафонова Н.В.)

Задание. Для функции 𝑦 = (2𝑥 + 3)𝑒^5𝑥 :

1. 
   Найти область определения, точки разрыва.
   
2. 
   Исследовать функцию на четность, периодичность.
   
3. 
   Исследовать поведение функции на концах области определения. Указать асимптоты.
   
4. 
   Найти промежутки монотонности. Точки экстремума.
   
5. 
   Найти промежутки выпуклости. Точки перегиба.
   
6. 
   Найти площадь фигуры между кривыми 𝑦 = (2𝑥 + 3)𝑒^5𝑥, 𝑥 = 0, 𝑥 = 2, 𝑦 = 0.
   

Результаты исследования

Область определения, точки разрыва:	Ответ: (−∞,∞) или x ∈ R; Разрывов нет, поскольку нет дробей с неизвестными в знаменателе. Ответ: Нет разрывов
Четность, периодичность:	С помощью соотношений: f= f(-x) и f= -f(-x) -f(-x) = -(-2x + 3)e-5x - НЕТ f(-x) = (-2x + 3)e-5x - НЕТ Ответ: функция ни чётная, ни нечётная; не периодическая.
Поведение на концах области определения:	Используем степень и старший коэффициент для определения поведения. Ответ: Не является многочленом
Асимптоты:	Нет вертикальных асимптот(т.к. вертикальные асимптоты находятся в точках бесконечного разрыва непрерывности). Горизонтальные асимптоты: y=0; Нет наклонных асимптот(т.к. степень числителя меньше или равна степени знаменателя).
Промежутки монотонности:	Возрастает на промежутках (-∞ ;-17/10), убывает: (-17/10; +∞)
Точки экстремума:	Найдем, где первая производная равна 0, чтобы найти локальные максимумы и минимумы. (−17/10; −2/5e17/2) — локальный минимум Максимума нет.
Промежутки выпуклости:	(-∞ ;-19/10) – выпукла; (-19/10; +∞) - вогнута
Точки перегиба:	x1 = -19/10 – точка перегиба
Площадь криволинейной трапеции.	S= 2,907 * 104

Решение:

Горизонтальные асимптоты:

Вычислим limx→−∞(2x+3)e^5x чтобы определить горизонтальную асимптоту.

Перепишем (2x+3)e^5x в виде 2x+3/e^-5x.

limx→−∞2x+3/e^−5x

Применим правило Лопиталя.

limx→−∞−2/5e^−5x

Вычислим предел.

−2/5limx→−∞1/e^−5x-25

Поскольку числитель стремится к вещественному числу, а знаменатель неограничен, дробь 1/e^−5x стремится к 0.

Умножим на 0

−2/5⋅0=0

Ответ: горизонтальные асимптоты: y=0

Находим интервалы возрастания и убывания. Первая производная.

f'(x) = 5·(2·x+3)·e^5·x+2·e^5·x


или

f'(x)=(10·x+17)·e^5·x


Находим нули функции. Для этого приравниваем производную к нулю

(10·x+17)·e^5·x = 0


Откуда:

x₁ = -17/10

(-∞ ;-17/10)	(-17/10; +∞)
f'(x) < 0	f'(x) > 0
функция убывает	функция возрастает

В окрестности точки x = -17/10 производная функции меняет знак с (-) на (+). Следовательно, точка x = -17/10 - точка минимума.

Найдем интервалы выпуклости и вогнутости функции. Вторая производная.

f''(x) = 5·(10·x+17)·e^5·x+10·e^5·x


или

f''(x) = (50·x+95)·e^5·x


Находим корни уравнения. Для этого полученную функцию приравняем к нулю.

(50·x+95)·e^5·x = 0


Откуда точки перегиба:

x₁ = -19/10

(-∞ ;-19/10)	(-19/10; +∞)
f''(x) < 0	f''(x) > 0
функция выпукла	функция вогнута

Площадь криволинейной трапеции.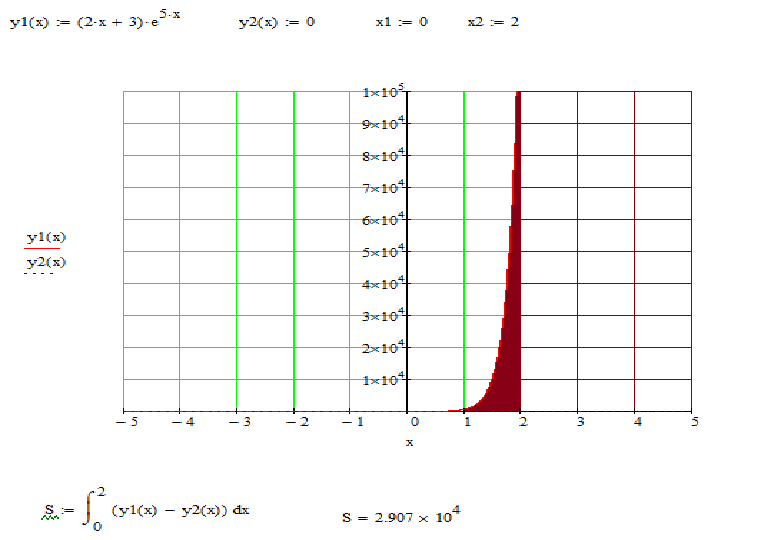