Контрольная работа. Итоговой диагностической работы по математике для учащихся 5х классов общеобразовательных учреждений Назначение диагностической работы

• Название: Итоговой диагностической работы по математике для учащихся 5х классов общеобразовательных учреждений Назначение диагностической работы
• Анкор: Контрольная работа
• Дата: 01.06.2022
• Размер: 42.8 Kb.
• Имя файла: К р.docx
• Тип: Документы; #561522

СПЕЦИФИКАЦИЯ

итоговой диагностической работы по математике

для учащихся 5-х классов общеобразовательных учреждений
1. Назначение диагностической работы

Диагностическая работа проводится в конце учебного года с целью определения уровня подготовки обучающихся 5-х классов общеобразовательных учреждений в рамках мониторинга достижений планируемых результатов освоения основной образовательной программы для образовательных учреждений, участвующих в переходе на ФГОС ООО.

Диагностическая работа охватывает содержание, включенное в массовые учебно-методические комплекты по математике, используемые в 5-х классах.

2. Структура диагностической работы

Работа состоит из 2 частей. Учащиеся на конец учебного года должны продемонстрировать

знания, умения, навыки : складывать, вычитать, делить, умножать десятичные дроби, решать текстовые задачи на нахождение нескольких процентов от числа; находить часть от числа, решать уравнения, решать задачи с помощью уравнений; находить среднее арифметическое нескольких чисел, знать виды углов, знать формулу пути, строить углы заданной градусной меры, решать текстовые задачи на вычисление части угла.

Часть 1 данной работы содержит 9 заданий базового уровня;

Часть 2 данной работы содержит 3 задания повышенного уровня;

Каждый вариант диагностической работы состоит из 12 заданий: шести с выбором одного правильного ответа (ВО), двух заданий с кратким ответом (КО), одного задания на установление соответствия(УС) и трех заданий с развернутым ответом (РО).

В каждом варианте представлены как задания базового уровня сложности, так и задания повышенного уровня сложности

3. Времявыполнения работы

На выполнение всей диагностической работы отводится 40 минут.4. Система оценивания отдельных заданий и работы в целом Верное выполнение каждого из заданий 1 – 9 оценивается в 1 балл. Задание 10-12 оценивается 0, 1 или 2 баллами (см. критерии оценивания). Максимальный первичный балл за выполнение всей работы – 15 баллов. Задание с кратким ответом или с выбором ответа считается выполненным, если записанный ответ совпадает с эталоном. Задание с развернутым ответом оценивается экспертом (учителем) с учетом правильности и полноты ответа в соответствии с критериями оценивания. Задание, оцениваемое в 2 балла, считается выполненными верно, если ученик выбрал правильный путь решения и в письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется 2 балла. Если в решении допущена ошибка , не имеющая принципиального характера и не влияющая на общую правильность хода решения, то выставляется 1 балл. 0 баллов получит ученик, если не получен верный ответ и неверный ход рассуждения. За выполнение диагностической работы образовательное учреждение может выставить обучающимся отметки по пятибалльной шкале после выполнения диагностической работы.

Для получения отметки «5» достаточно набрать 11 и более баллов.

Для получения отметки «4» достаточно набрать 8-10 баллов

Для получения отметки «3» достаточно набрать 5-7 баллов

Оценка «2» ставится, если ученик набрал меньше 5 баллов.

№	Часть работы	Тип заданий	Количество заданий	Максимальный первичный балл
1	Часть 1	С кратким ответом в виде одной цифры, которая соответствует номеру правильного ответа	6	1
2	Часть 1	В виде числа, последовательности цифр	3	1
3	Часть2	С развернутым ответом	3	2
ИТОГО			12	15

Обобщенный план варианта диагностической работы

№ п/п	Основные проверяемые требования к математической подготовке	Уровень сложности	Максимальный балл	Тип задания
1	Уметь выполнять деление и вычитание десятичных дробей	Б	1	ВО
2	Уметь располагать десятичные дроби в порядке возрастания	Б	1	ВО
3	Уметь решать задачи с обыкновенными дробями	Б	1	ВО
4	Уметь округлять десятичные дроби.	Б	1	ВО
5	Уметь выполнять умножение и деление дробей на 10, 100, 0,1, 0,001 ит.д.	Б	1	КО
6	Уметь решать уравнение	Б	1	ВО
7	Уметь решать задачу на проценты	Б	1	КО
8	Уметь установить соответствие между рисунком и величиной угла	Б	1	УС
9	Уметь находить среднее арифметическое нескольких чисел	Б	1	ВО
10	Уметь решать задачи на движение	П	2	РО
11	Уметь решать задачи с помощью уравнения	П	2	РО
12	Уметь находить градусную меру угла.	П	2	РО

1 ВАРИАНТ

1. Найдите значение выражения: 0,4 + 1,85 : 0,5

1) 4,5 2) 4,1 3) 3,7 4) 0,77

2. Расположите в порядке возрастания числа: 1,275; 0,128; 1,281; 12,82; 1,027

1) 1,275; 0,128; 1,281; 12,82; 1,027
2) 0,128; 1,281; 1,275; 1,027; 12,82
3) 0,128; 1,027; 1,275; 1,281; 12,82
4) 0,128; 1,275; 1,027; 1,281; 12,82

3. Задача: От веревки длиной 120 см отрезали 1/3  часть. Какова длина оставшейся веревки?

А) 180 см Б) 80 см В) 40 см Г) 60 см

4. Округлите 2,34798 до десятых.

1) 2,4

2) 2,34

3) 2,35

4) 2,3

5. Выполните умножение и деление

121,39 · 0,01 = ………

17,45 · 1000 = ………

314,51 :100 = ………

0,27 : 0,1 = ……………

6. Решите уравнение : 1,5х+1,2=4,8

1) 4

2) 50

3) 2,4

4) 2,04

Ответ: …………

7 .Задача. В яблоневом саду собрали 8400 кг яблок. На долю антоновских яблок приходится 45% всего урожая. Сколько килограммов антоновских яблок собрали в саду?

Ответ: …………

8. Установите соответствие.



Ответ: 1…… 2…… 3 ……4 ……

9. На спортивных соревнованиях трое судей оценили выступление гимнаста оценками 5,7; 5,5; 5,6. Найдите среднюю арифметическую оценку гимнаста.

1) 5,6

2) 5,5

3) 5,7

4) 5,55

Задания №10, №11, №12 решить с записью полного решения.

10. Собственная скорость лодки 5 км/ч, а скорость течения реки 2,2 км/ч. Сначала лодка прошла 1,2 ч против течения, а затем 0,8 ч по течению. Какой путь лодка прошла за всё это время?

11. Решите задачу с помощью уравнения. Два поля занимают площадь 156,8 га. Одно поле на 28,2 га больше другого. Найдите площадь каждого поля.

12. Начертите угол MKN, равный140°. Лучом KP разделите этот угол на два угла так, чтобы угол PKN был равен 55°. Вычислите градусную меру угла MKP.

Вариант 2.

1. Найдите значение выражения: 6,54 – 3,24 : 1,5

1) 2,2 2) 2,16 3) 3,3 4) 4,38

2. Расположите в порядке убывания числа: 1,583; 1,045; 1,451; 0,407; 1,513.

1) 1,583; 1,045; 1,451; 0,407; 1,513
2) 1,583; 1,513; 1,451; 1,045; 0,407
3) 1,513; 1,583; 1,451; 0,407; 1,045
4) 0,407; 1,045; 1,451; 1,513; 1,583

3. Задача :Надо отремонтировать 210 км дороги. В первую неделю отремонтировали   дороги. Сколько километров дороги осталось отремонтировать?

А) 30км Б) 180 км В) 60 км Г) 160 км

4.Округлите 5,24752 до сотых.

1) 5,25

2) 5,248

3) 5,24

4) 5,23

5. Выполните деление и умножение

87.54 : 10 = …………
87,54 : 0,001 = ………
3,84 * 1000 = ………
0,47 * 0,1 = ………

6. Решите уравнение: .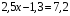

1) 8,5

2) 3,4

3) 2,36

4) 6

Ответ: …………

7. Задача .В старших классах 120 учащихся. Из них 85% работали летом на ферме. Сколько учащихся старших классов работали летом на ферме?

Ответ: …………………

8. Установите соответствие.

1. 12°	А) тупой угол
2. 91°	Б) острый угол
3. 90°	В) прямой угол
4. 180°	Г) развернутый угол

Ответ: 1 …… 2 …… 3 …… .4……

9. Купили трёх поросят массой 27,3 кг, 30,5 кг, 18,7 кг. Найдите среднюю массу купленных поросят.

1) 27,3

2) 25,5

3) 30,5

4) 38,25

Задания №10, №11, №12 решить с записью полного ответа.

10. Лодка шла по течению 0,8 ч и против течения 0,3 ч. Собственная скорость лодки 3,8 км/ч , а скорость течения 1,3 км/ч. Какой путь прошла лодка за это время?

11. Решите задачу с помощью уравнения. Два поля занимают площадь 79,9 га. Площадь первого поля в 2,4 раза больше второго. Какова площадь каждого поля?

12. Начертите угол MOK, равный 155°. Лучом OD разделите этот угол так, чтобы получившийся угол MOD был равен 103°. Вычислите градусную меру угла DOK.

Ответы

Номер задания	Вариант 1	Вариант 2
1	2	4
2	3	2
3	2	3
4	1	1
5	1,2139, 17450, 3,1415, 2,7	8,754, 87540, 3840, 0,047
6	3	2
7	3780	102
8	1-Б, 2-А, 3-В, 4-Г	1-Б, 2-А, 3-В, 4-Г
9	1	2
10	9,12км	4,83км
11	64,3га, 92,5га.	23,5га, 56,4га.
12	85	52

1 вариант

Решение задачи № 10

1. 
   5-2,2=2,8(км/ч)- скорость лодки против течения реки.
   
2. 
   5+2,2=7,2(км/ч)- скорость лодки по течению реки.
   
3. 
   2,8*1,2=3,36 (км) прошла лодка против течения
   
4. 
   7,2*0,8=5,76 (км) прошла лодка по течению реки
   
5. 
   3,36+5,76=9,12(Км) прошла лодка всего/
   

Ответ: 9,12км

Решение задачи № 11

х (га)-площадь 1 поля

х+28,2(га)- площадь 2 поля

Два поля занимают площадь 156,8 га.

х+х+28,2=156,8

2х=156,8-28,2

2х=128,6

Х=128,6:2

Х=64,3 (га) площадь 1 поля

Если х=64,3, то 64,3+28,2=92,5(га) площадь 2 поля

Ответ: 64,3га, 92,5га.

Решение задачи № 12

< MKP = 140-55= 85

2 вариант

Решение задачи № 10

1. 
   3,8-1,3=2,5(км/ч)- скорость лодки против течения реки.
   
2. 
   3,8+1,3=5,1(км/ч)- скорость лодки по течению реки.
   
3. 
   2,5*0,3=0,75 (км) прошла лодка против течения
   
4. 
   5,1*0,8=4,08 (км) прошла лодка по течению реки
   
5. 
   0,75+4,08=4,83(Км) прошла лодка всего.
   

Ответ: 4,83км

Решение задачи № 11

х (га)-площадь 1 поля

2,4х (га)- площадь 2 поля

Два поля занимают площадь 79,9 га.

х+2,4х=79,9

3,4х=79,9

х=79,9 :3,4

Х=23,5

Х=23,5 (га) площадь 1 поля

Если х=23,5, то 79,9-23,5=56,4 (га) площадь 2 поля

Ответ: 23,5га, 56,4га.

Решение задачи № 12

< DOK = 155-103=52