Практическое задание. Из генеральной совокупности извлечена выборка объема n. Найти среднее значение, дисперсию, среднее квадратичное отклонение, исправленную дисперсию, коэффициент вариации, моду и медиану

• Название: Из генеральной совокупности извлечена выборка объема n. Найти среднее значение, дисперсию, среднее квадратичное отклонение, исправленную дисперсию, коэффициент вариации, моду и медиану
• Дата: 11.06.2022
• Размер: 29.72 Kb.
• Имя файла: Практическое задание.docx
• Тип: Документы; #585230

Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления Форма обучения: заочная/очно-заочная

ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

Математические методы в психологии



Группа
Студент

МОСКВА 2021

Задание 1.

Из генеральной совокупности извлечена выборка объема n . Найти среднее значение, дисперсию, среднее квадратичное отклонение, исправленную дисперсию, коэффициент вариации, моду и медиану.

xi	9,5	10	10,5	11	11,5	12	12,5
ni	3	15	30	15	5	4	2

Решение:

xi	9,5	10	10,5	11	11,5	12	12,5	∑
ni	3	15	30	15	5	4	2	74
xini	28,5	150	315	165	57,5	48	25	789
(xi-X)2*ni	4,0368	6,534	0,768	1,734	3,528	7,1824	6,7712	30,5544

Среднее значение X = (1/n) * ∑x_i n_i = (1/74) * 789 = 10,66

Дисперсия D = (1/n) * ∑((x_i -X)² * n_i) = (1/74) * 30,55=0,412

Исправленная дисперсия S² = n/(n-1) * D = 74/73 * 0,412=0,417

Среднеквадратичное отклонение σ = √D = 0,642

Исправленное среднеквадратичное отклонение S = 0,646

Коэффициент вариации V = σ/X * 100% = 0,642/10,66*100% = 6,022%

Мода – величина с наибольшей частотой Мо = 10,5

Медиана - величина, находящаяся в середине ряда Ме = 10,5
Задание 2
Дан следующий вариационный ряд:

i	1	2	3	4	5	6	7	8	9	10
xi	2	2	3	3	5	5	5	6	6	6

Требуется:

1) Построить полигон распределения

2) Вычислить выборочную среднюю, дисперсию, моду, медиану.
Решение:

xi	2	3	5	6
ni	2	2	3	3

График полигона частот: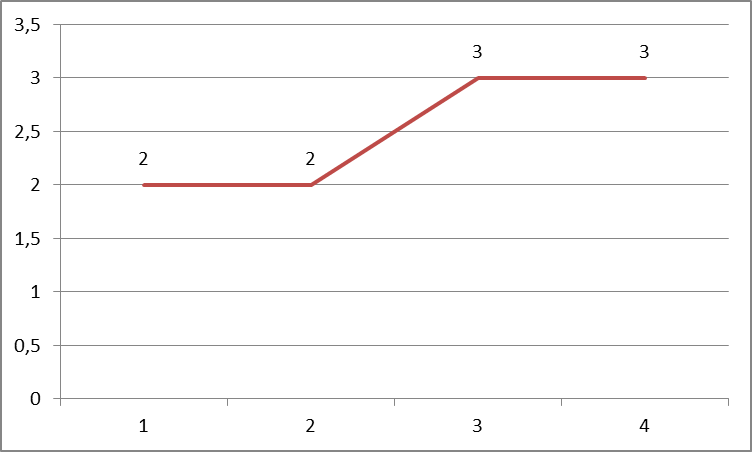



Выборочная средняя:

X = (1/n) * xini = (1/10)*(2*2+3*2+5*3+6*3) = 43/10 = 4,3

Выборочная дисперсия:

D = (1/n) * xi² ni – X² = (1/10)*(4*2+9*2+25*3+36*3) – 18,49 = 2,41

Выборочное среднеквадратичное отклонение:

 = D = 2,411,552.

Мода равна варианту с наибольшей частотой: 5;6 (две моды)

Медиана равна среднему варианту выборки: 5.
Задание 3
Были протестированы две группы студентов. Тест содержал 60 вопросов. Указано число правильных ответов каждого участника теста. Можно ли утверждать, что одна из групп превзошла другую группу по результатам теста?

Группа 1: 55, 45, 42, 40

Группа 2: 46, 41, 38, 35, 34
Решение:

Используем критерий U - критерий Манна-Уитни.

Гипотезы:

Н0: Уровень признака в группе 2 не ниже уровня в группе 1.

H1: Уровень признака в группе 2 ниже уровня признака в группе 1.

Соблюдены ограничения критерия U:

1. В каждой выборке должно быть не менее 3 наблюдений: n1,n2≥3; допускается, чтобы в одной выборке было 2 наблюдения, но тогда во второй их должно быть не менее 5.

2. В каждой выборке должно быть не более 60 наблюдений;

n1,n2≤60. Однако уже при n1,n2>20 ранжирование становится достаточно трудоемким.

Ранжируем наблюдения:

Меньшему значению начисляется меньший ранг. Наименьшему значению начисляется ранг 1. Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений.

Количество ранжируемых значений = 4 + 5 = 9.

Минимум 34 – ранг 1. Максимум 55 – ранг 9.

Если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны.

Группа 1	Ранг	Группа 2	Ранг
55	9
		46	8
45	7
42	6
		41	5
40	4
		38	3
		35	2
		34	1
Сумма	26	Сумма	19

Общая сумма = 9*(9+1)/2 = 45 = 26 + 19

Мы видим, что по уровню невербального интеллекта более «высоким» рядом оказывается выборка группы 1. Именно на эту выборку приходится большая ранговая сумма: 26.

Теперь мы готовы сформулировать гипотезы:

H0: Группа 1 не превосходит группу 2 по результатам теста.

Н1: Группа 1 превосходит группу 2 по результатам теста.

Определить значение U по формуле: U = (n₁*n₂) + n_x(n_x+1)/2 – T_x

где n₁ - количество испытуемых в группе 1; n₂ – количество испытуемых в группе 2; Т_x - большая из двух ранговых сумм; n_x - количество испытуемых в группе с большей суммой рангов.

Определяем эмпирическую величину U:

UЭМП = (4*5)+4(4+1)/2 – 26 = 4

Определяем критические значения для n₁=4, n₂=5.

Uкр = 2 при p ≤ 0,05;

Uкр = 0 при p ≤ 0,01.

4 больше и 2 и 0, Uэмп > Uкp.

H0 принимается.

Ответ: Группа 1 не превосходит группу 2 по результатам теста.

Задание 4
Психолог просит супругов проранжировать девять личностных черт, имеющих определяющее значение для семейного благополучия. Задача заключается в том, чтобы определить, в какой степени совпадают оценки супругов по отношению к ранжируемым качествам.

Заполните таблицу и, посчитав коэффициент ранговой корреляции Спирмена, ответьте на поставленный вопрос.

Черты личности	№	Муж	Жена
Ответственность	1
Общительность	2
Сдержанность	3
Выносливость	4
Жизнерадостность	5
Терпеливость	6
Решительность	7
Оптимизм	8
Надежность	9

Решение:

Заполняем таблицу. Далее, рассчитываем коэффициент ранговой корреляции Спирмена и составляем расчетную таблицу.

№	1	2	3	4	5	6	7	∑
РангX, dx	2	3	4	6	5	1	7	28
РангY, dy	2	5	1	7	6	3	4	28
(dx-dy)2	0	4	9	1	1	4	9	28

Вычисляем коэффициент ранговой корреляции Спирмена.

p = 1 – 6 * ( (∑d²) / (n³- n) ) = 1 – 6 * ( (28) / (7³- 7) ) = 0,5
Ответ:

Согласованность между мнениями супругов прямая, но умеренная.