ИЗМЕРЕНИЕ ДАВЛЕНИЙ. Контрольная работа. Измерение давлений

• Название: Измерение давлений
• Анкор: ИЗМЕРЕНИЕ ДАВЛЕНИЙ
• Дата: 16.02.2023
• Размер: 0.49 Mb.
• Имя файла: Контрольная работа.docx
• Тип: Реферат; #940586
• страница: 2 из 3

3. Расчет характеристик пружинных манометров и датчиков давления

Рассмотрим методику расчета статических и динамических характеристик пружинных манометров и датчиков давления.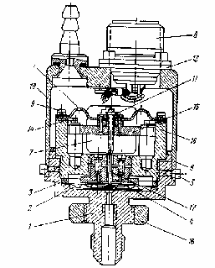



Рис.12. Конструкция датчика давления с индуктивным преобразователем:

1 корпус; 2 мембрана; 3 кольцо; 4 упор; 5 винт; 6 прокладка; 7 катушка; 8 вилка; 9 винт; 10 кожух; 11гайка; 12 пружина; 13 прокладка; 14 винт; 15 якорь; 16 крышка приемного узла; 17 шток; 18 контргайка

На рис.14 представлена структурная схема датчика абсолютного давления, отображающая процесс преобразования измеряемого давления р₁в выходной электрический сигнал U. Звенья структурной схемы выполняют следующие функции.

Звено 1 преобразует измеряемое давление р₁в давление p₁; дей­ствующее в корпусе манометра; в этом звене учитывается запаздывание имеющее место при передаче давления по трубопроводу. Звено 2 преобразует давление р₁в движущую силу Р_дв; это звено отображает силовую характеристику чувствительного элемента. Звено 3 преобразует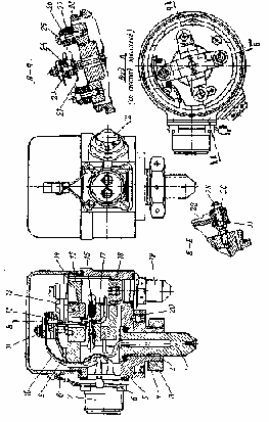



Рис.13. Конструкция унифицированного сигнализатора давления:

1 трубопровод; 2, 26 втулки; 3, 19штуцера; 4 гайка; 5 основание; 6, 9, 20, 25  винты; 7 штепсельная вилка; 8 корпус; 10 провод; 11 наконечник; 12 центр; 13 упор; 14 кронштейн; 15 шток; 16 мембранная коробка; 17 прокладка; 18 заглушка с сеткой; 21 нижняя пружина; 22 верхняя пружина; 23, 24 контакты; 27, 28 кольца; 29 шпилька; 30 гайка; 31 платинка; 32 заглушка

силу Р_дв в линейное перемещение S подвижной системы; это звено учитывает упругие и демпфирующие свойства и инерционные массы всех подвижных частей как чувствительного элемента, так и передаточно-множительного механизма. Звено 4 осуществляет преобразование линейного перемещения S в угловое перемещение ; звено 4 отображает уравнение кинематики передаточно-множительного механизма. Звено 5 (потенциометр, индуктивный преобразователь и т. п.) преобразует угловое перемещение  в электрическую величину Z.

При расчете статической характеристики манометра структурную схему можно упростить, поскольку для установившегося режима измерения р₁₌р₁, кроме того, демпфирующие и инерционные силы отсутствуют; это позволяет объединить звенья 1, 2 и 3 и рассматривать их как единое звено, осуществляющее преобра­зование р₁в Sв соответствии со статической характеристикой упругого чувствительного элемента (см. пунктир на рис.14):

S=_1-3( p₁ ).

Решая это уравнение совместно с уравнениями звеньев 4 и 5

=₄( S );

Z=₅( ),

получим статическую характеристику датчика:

Z=₅₄_1-3( p₁ ).

Чувствительность

S=S_1-3S₄S₅,

где S_1-3= 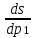 чувствительность упругого элемента;

S₄₌  чувствительность (передаточное отношение) механизма;

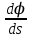S₅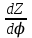₌  чувствительность электрического преобразователя перемещений.
Для получения равномерной шкалы необходимо, чтобы S=const, что возможно в двух случаях:

1. 
   Преобразующие звенья - чувствительный элемент, механизм и электрический преобразователь обладают линейной характеристикой, т. е. S_1-3=const, S₄=const и S₅=const.
   
2. 
   Нелинейность характеристики чувствительного элемента компенсируется нелинейностью механизма и электрического преобразователя так , что в любой точке шкалы S_1-3= .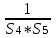
   

Для нахождения передаточной функции датчика предварительно определим передаточные функции звеньев структурной схемы на рис.14.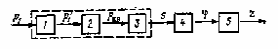



Рис.14. Структурная схема датчика абсолютного давления:

1 звено, отображающее процесс передачи давления по трубопроводу; 2звено, отображающее силовую характеристику упругого чувствительного элемента; 3 упругая подвижная система; 4 передаточно-множительный механизм; 5 потенциометр

Передаточная функция звена 1, преобразующего р₁ в р₁’, следует из линеаризованного дифференциального уравнения процесса передачи давления по трубопроводу, которое может быть получено следующим образом.

Масса воздуха , находящегося в корпусе манометра:

m₁= кг, (1)

где   объем воздуха внутри корпуса в м³,

  плотность воздуха в кг/м³.

Уравнение состояния газа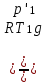

= н/м³, (2)

где R  газовая постоянная в м/град;

T  температура воздуха внутри корпуса в К;

g=9.81 м/сек².

Подставив (2) в (1), получим

m₁= 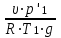. (3)

Продифференцируем выражение (3), считая при этом приближенно =constиT=const: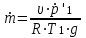

. (4)

Согласно закону Пуазейля массовый расход воздуха через трубопровод при ламинарном потоке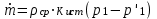

, (5)

где _{ср } средняя плотность воздуха в трубопроводе в кг/м³;

к_ист= 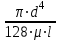коэффициент истечения в м⁵/нсек;

dдиаметр трубопровода в м;

l длина трубопровода в м;

  вязкость воздуха в н·сек/м².

Приравнивая правые части выражений (4) и (5), получим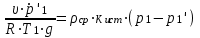

,

или (6)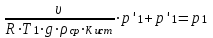

.

В выражении (6) можно заменить RT₁gρ_ср=р_ср,, где р_ср среднее давление воздуха в трубопроводе в н/м².

Тогда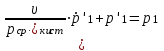

.

Обозначив далее постоянную времени

T_o= 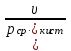, (7)

получим в окончательном виде дифференциальное уравнение звена 1: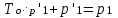

(8)

Если приближенно считать Т_о=const( пренебрегая изменением , р_ср и к_ист), то передаточная функция звена 1 будет

W₁(p)= 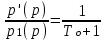. (9)

Если внутренний объем трубопровода соизмерим с объемом корпуса датчика, то при определении постоянной времени Т_о величину  следует приближенно брать равной сумме внутреннего объема корпуса и половине внутреннего объема трубопровода.

При использовании длинных трубопроводов следует учитывать также нелинейное запаздывание Т₁, которое равно времени прохождения звуковой волны от начала трубопровода к концу: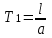

,

где а скорость звука в м/сек.

При этом передаточная функция звена 1 будет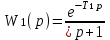

. (10)

Передаточная функция звена 2 определяется из линеаризованного уравнения силовой характеристики чувствительного элемента: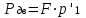

н,

где F эффективная площадь чувствительного элемента в м², откуда передаточная функция звена 2 будет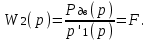

(11)

Передаточная функция звена 3 (подвижной системы) определяется по формуле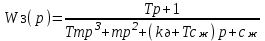

. (12)

При использовании этой формулы следует иметь ввиду, что в качестве воздушного демпфера здесь служит чувствительный элемент, который можно рассматривать как поршень с площадью F, равной эффективной площади сильфона, и объёмом , равным внутреннему объему сильфона. В качестве капилляра, через который происходит истечение воздуха из демпфера, используется трубопровод ( или дополнительное дросселирующее отверстие, расположенное на входе в чувствительный элемент ) диаметром db длинной l. Вычисление параметров T_uи k_д, входящих в выражение (12), следует вести по формулам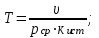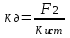

(*)

, (**)

где

р_ср=0.5(р₁+р’₁); к_ист= .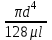

Входящий в формулу (12) параметр с_ж представляет собой приведенный коэффициент линейной жесткости, учитывающий жесткость упругого чувствительного элемента и жесткость дополнительной пружины, выбирающей люфты. Параметр m  это приведенная масса подвижной системы.

Передаточная функция звена 4 определяется из линеаризованного уравнения кинематики механизма

=S₄s,

где S₄ передаточное отношение механизма в рад/м.

Отсюда передаточная функция звена 4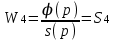

. (13)

Передаточная функция звена 5 определяется из уравнения электрического преобразователя Z=S₅, откуда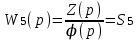

. (14)

Общая передаточная функция датчика давления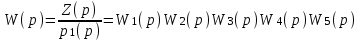



или с учетом выражений (10)(14)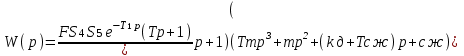

.

Если сравнить между собой постоянные времени Т_о и Т, определяемые по формулам (7) и (*), нетрудно заметить , что для изотермического процесса Т_о=Т; учитывая это обстоятельство и пренебрегая постоянной времени Т₁ ввиду ее малости , получим упрощенное выражение передаточной функции датчика давления в виде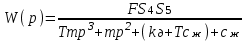

. (15)

Необходимо иметь ввиду, что приведенные расчеты выполнены без учета сухого трения, действующего в механизме прибора.

Расчет с учетом сухого трения показывает, что при свободных колебаниях системы 2-го порядка затухание колебаний за один период не зависит от частоты и равно 4, где  — зона застоя прибора. Поэтому сухое трение особенно эффективно гасит колебания на больших частотах. Так, при включении давления воздуха колебания стрелки манометра, имеющего собственную частоту 500 гц и зону застоя 0,5%, за каждый период будут уменьшаться на 2% и полностью затухать через 50 колебаний, т. е. за 0,1 сек.

4.Погрешности пружинных манометров и датчиков давления

Пружинным манометрам свойственны следующие инструментальные погрешности.

1.Погрешности характеристики (шкаловые погрешности), вызываемые неполной взаимной компенсацией нелинейности характеристик чувствительного элемента и передаточно-множительного механизма, а в датчиках— и электрического преобразователя. Эти погрешности минимизируют путем инди­видуальной регулировки механизма в изготовленных образцах приборов и датчиков.

Существуют специальные механизмы, позволяющие свести к нулю погрешности во многих точках характеристики. Примером такого механизма служит механи­ческий. корректор шкаловых погрешностей, в котором ролик скользит по кулачку, выполненному из гибкой ленты; кривизна кулачка может плавно изменяться за счет местного изгиба ленты с помощью регулировочных винтов (рис.15). Ролик укреплен на рычаге, который при своем повороте сообщает выходной оси дополнительное угловое перемещение того или другого знака. Знак дополнительного перемещения зависит от того, попадает ли ролик на выступ или впадину кулачка.



Рис.15. Схема механизации корректора:

1 входная ось; 2 скоба; 3 поперечная ось; 4 рычаг; 5ролик; 6 гибкая кольцевая лента; 7 ведущий поводок; 8 ведомый поводок; 9 выходная ось; 10 спиральная пружина; 11 стрелка или щетка потенциометра; 12 регулировочный винт

2. Погрешности, обусловленные влиянием вредных сил, к числу которых относятся прежде всего силы трения в передаточно-множительном механизме и электрическом преобразователе, силы от неуравновешенности подвижных частей, электромагнитные или электростатические силы от взаимного притяжения или отталкивания подвижных и неподвижных частей электрического преобразователя. Уменьшение этих погрешностей возможно следующими путями:

а) снижением вредных сил за счет улучшения качества опор, тщательной балансировки механизма и т. п. Повышение точно­сти балансировки позволяет ослабить натяги пружин, выбираю­щих люфты, что в свою очередь способствует уменьшению сил трения;

б) увеличением эффективной площади чувствительного элемента;

в) применением дифференциальных электрических преобразователей, у которых в начальном положении силы притяжения взаимно скомпенсированы;

г) применением следящих систем, разгружающих чувствительный элемент от сил трения.

3. Температурные погрешности манометров, вызываемые влиянием температуры окружающей среды на физические параметры материалов и геометрические размеры деталей.

Наиболее существенно температура влияет на модуль упругости чувствительного элемента.

Линеаризованная зависимость модуля упругости от температуры имеет вид

Е=Е_о(1+_Е) н/м²,

Где Е_о начальное значение Е (при =_о) в н/м²;

_Е  температурный коэффициент Е;

= - _о С.

Характеристика чувствительного элемента дифференциального манометра связана с модулем упругости соотношением

р=Еf(s) н/м².

Относительная величина температурной погрешности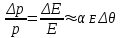

.

Например, при значении _Е=-210^-4 и =-80 величина относительной температурной погрешности 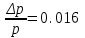или 1,6 %.

Влияние температуры на геометрические размеры чувствительного элемента и передаточно-множительного механизма выражается зависимостью

l=l_o(1+_l) м,

где l геометрический размер;

_lкоэффициент линейного расширения.

Это влияние сказывается на показаниях прибора значительно слабее благодаря тому, что температурные коэффициенты _l линейного расширения металлов на порядок меньше, чем температурные коэффициенты _Е модуля упругости.

Температура влияет также на величину остаточного давления р_ост внутри анероидов (вакуумированных чувствительных элементов), применяемых в манометрах абсолютного давления. При изменении температуры на величину  возникает погрешность 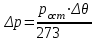. Наконец, при изменении температуры может изменяться выходной параметр R, L, М или С электрического преобразователя.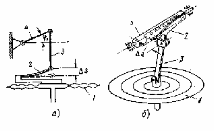



Рис.16. Схемы биметаллических компенсаторов:

а 1-го рода; б 2-го рода; 1 мембранная коробка; 2 биметаллическая пластина; 3 шатун; 4 кривошип; 5 ось кривошипа

Уменьшение температурных погрешностей достигается следующими способами:

а) изготовлением чувствительных элементов из сплава типа элинвар, обладающих весьма малым температурным коэффициентом модуля упругости;

б) снижением остаточного давления внутри анероидов путем более тщательного вакуумирования их;

в) введением в конструкцию прибора специальных биметаллических компенсаторов, которые вызывают в зависимости от температуры приращение показания прибора, равное по величине и противоположное по знаку температурной погрешности прибора.

Различают биметаллические компенсаторы 1 и 2-го рода.

Действие компенсаторов 1-го рода (рис.16, а) основано на введении последовательно с упругим чувствительным элементом кинематического звена, выполненного в виде консольно закрепленной биметаллической пластины, линейное перемещение свободного конца которой s, пропорциональное приращению температуры, складывается с прогибом s упругого чувствительного элемента (или вычитается из него). Расчет величины s для биметаллического компенсатора пластинчатого типа (см. рис.19, а) производится по формуле: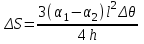

м, (16)

где hтолщина биметаллической пластины в м;

₁и ₂коэффициенты линейного расширения компонент биметалла;

l длина пластины в м;

  приращение температуры С.

Компенсатор 1-го рода компенсирует только аддитивную температурную погрешность.

Действие компенсаторов 2-го рода (см. рис. 16,6) основано на введении в кривошип кинематического звена, выполненного в виде биметаллической пластины, перемещение свободного конца которой, пропорциональное приращению температуры, вызывает увеличение или уменьшение плеча кривошипа на величину а, которая определяется так же, как и величина s для компенсатора 1-го рода, по формуле (16). Характер влияния компенсатора 2-го рода на приращение показаний прибора зависит от начального угла ₁ установки кривошипа (см. рис.16, а). Если этот угол близок к нулю, т. е. если при s = 0 кривошип примерно перпендикулярен шатуну, то приращение а плеча кривошипа почти не вызывает начального поворота кривошипа, а лишь из­меняет передаточное отношение механизма. Поэтому при ₁=0 вводимая компенсатором 2-го рода поправка носит чисто мультипликативный характер. Относительная величина этой поправки равна 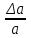= , где а — плечо кривошипа. Если же ₁0, то изменение температуры вызывает начальный поворот кривошипа при s = 0, и в этом случае вводимая компенсатором 2-го рода поправка содержит как аддитивную, так и мультипликативную составляющие;

г) применением дифференциальных электрических преобразователей, выдающих два переменных параметра z₁ и z₂ и вклю­ченных по схеме делителя напряжений; при работе на высокоомную нагрузку дифференциальный преобразователь не имеет температурной погрешности, так как величина снимаемого напряжения от величины параметров z₁ и z₂ не зависит, а определяется соотношением z₁/z₂; важно обеспечить лишь равенство температурных коэффициентов параметров z₁ и z₂;

д) применением электрических компенсаторов, выполненных в виде проволочного или полупроводникового термосопротивлений и включаемых во внешнюю электрическую цепь так, чтобы ском­пенсировать температурные погрешности, вносимые всеми остальными элементами датчика.

4. Погрешности от люфтов в опорах, шарнирах и направляющих передаточно-множительного механизма. Для устранения погрешностей от люфтов на выходной оси передаточно-множительного механизма устанавливается спиральная пружина (волосок), которой дается начальный натяг. Величина натяга выбирается из тех соображений, чтобы во всем диапазоне углов поворота выходной оси момент, создаваемый пружиной вокруг своей оси, несколько превышал приведенный момент небаланса, умноженный на максимальную величину вибрационной перегрузки или перегрузки от линейных ускорений. Слишком большой натяг пружины нежелателен, так как он приводит к увеличению погрешностей от трения.

5. Погрешности от гистерезиса и упругого последействия. Снижение этих погрешностей достигается выбором материалов с хорошими упругими свойствами и улучшением режимов их термической обработки. Наименьшими погрешностями от гистерезиса и упругого последействия обладают чувствительные элементы, изготовленные из сплавов типа 47ХНМ и бериллиевой бронзы.

6. Погрешности от влияния давления окружающей среды. Эти погрешности возникают в манометрах со сдвоенными чувствительными элементами (см. рис.6 и 8) в случае неравенства их эффективных площадей. Для уменьшения погрешностей подбирают чувствительные элементы с возможно более близкими эффективными площадями.