ЛР8подг. ЛР8 подг. измерение сопротивлений токопроводящих моделей при помощи мостa уитстона
 Скачать 49.74 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра Физики отчет по лабораторной работе №8 по дисциплине «Физика» Тема: «ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ТОКОПРОВОДЯЩИХ МОДЕЛЕЙ ПРИ ПОМОЩИ МОСТA УИТСТОНА»
Санкт-Петербург 2020 Цель работы. Ознакомление с методом измерения сопротивлений при помощи моста постоянного тока; приобретение навыков расчета сопротивления проводников переменного сечения; определение удельных сопротивлений материалов токопроводящих моделей. 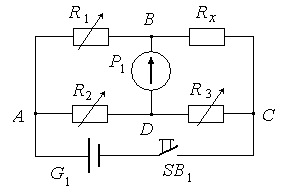 Схема установки (моста Уитстона):Мост состоит из четырёх резисторов, R1, R2, R3 – известны, Rx – необходимо найти. Клеммами А и С мост присоединён к источнику G1, а в диагональ BD моста включён нуль-индикатор (гальванометр) P1. Если сопротивления в плечах моста подобраны так, что напряжение UAC делится между R1 и Rx в ветви АВС в том же соотношении, что и между R2 и R3 в ветви ADC, то разность потенциалов между точками B и D равна нулю: тока через гальванометр нет и 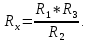 Такой мост называется сбалансированным. В качестве резисторов R1, R2, R3 используются многодекадные магазины образцовых резисторов, изменяя номиналы которых, добиваются баланса моста, а затем рассчитывают Rx. Измерения проводятся на двух моделях, имеющих сопротивления Rx1 и Rx2. Переключатель SA1 (на схеме не указан) обеспечивает включение в плечо моста резистора Rx1 либо Rx2. Основные теоретические положения. Сопротивление проводников зависит от их формы и размеров, от рода вещества и его состояния. Сопротивление проводника в форме цилиндра постоянного поперечного сечения: 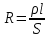 где l – длина проводника; S – площадь его поперечного сечения; 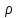 – удельное сопротивление материала проводника.Удельное сопротивление служит одной из основных электрических характеристик вещества. Зная 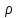, можно рассчитать размеры проводника, требуемые для получения заданного его сопротивления, или наоборот – сопротивление при известных геометрических размерах проводника.Выражениe 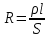имеет ограниченное применение: оно непригодно дляпроводников переменного сечения, в которых плотность тока не одинакова в любом сечении, например, при расчете сопротивления утечки цилиндрического конденсатора, заполненного проводящей средой. Рассчитывают такие сопротивления, разбивая (руководствуясь соображениями симметрии) проводники (или проводящую среду) на множество элементов длиной dl с поперечным сечением S так, чтобы плотность тока в любой точке отдельного элемента была одинаковой. Сопротивление каждого отдельного элемента 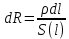 где S – площади поперечного сечения проводника, а сопротивление проводника на участке от точки 1 до точки 2 равно 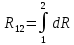 Если такое разбиение невозможно или зависимость S(l) слишком сложна, используют подобие электрического поля в однородной проводящей среде с током электростатическому полю в диэлектрике при условии, что удельное сопротивление проводящей среды много больше удельного сопротивления материала электродов. Иначе говоря, распределение потенциала в проводящей среде с током окажется таким же, как и в диэлектрике (или вакууме), если, не меняя размеров и формы электродов, их взаимного расположения и разности потенциалов между ними, проводящую среду заменить диэлектрической. При этом выполняется соотношение 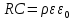 где R – сопротивление утечки между двумя электродами в проводящей среде с удельным сопротивлением 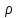; C – взаимная электроемкость электродов в среде с относительной диэлектрической проницаемостью 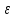 .Таким образом, расчет сопротивления утечки между электродами в проводящей среде можно свести к расчету взаимной электроемкости двух проводников, т. е., по существу, к задаче электростатики. Взаимная электроемкость электродов рассчитывается по формуле 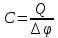 где Q – заряд на одном из электродов (на другом электроде имеется равный по модулю и противоположный по знаку заряд –Q); 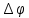 – разность потенциалов между электродами.Разность потенциалов находится криволинейным интегрированием электрического поля: 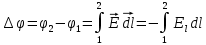 где El – касательная к пути интегрирования компонента вектора E. Путь интегрирования следует выбирать, руководствуясь соображениями простоты расчетов – например, при интегрировании вдоль силовой линии электрического поля El = E. Электрическое поле находится либо как суперпозиция полей электродов, либо по формуле Гаусса (если задача обладает подходящей симметрией), либо другим, не столь простым способом (методом изображений, замены переменных и т. п.). В результате расчета получится выражение для 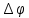в виде произведения Q на множитель, зависящий только от геометрии системы и диэлектрической проницаемости среды. Обратная этому множителю величина есть взаимная электроемкость этих электродов. Формула для расчета сопротивления утечки между электродами в проводящей среде получается из соотношения 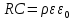. Следует также отметить, что из-за подобия распределения полей в проводящей среде и в диэлектрике проводящая среда с током может служить моделью для исследования электростатических полей. Например, вместотрудоемких расчетов или непосредственного измерения емкости какой-либо системы проводников сложной формы можно поместить модели этих проводников в проводящую среду, измерить сопротивление между ними, а затем найти емкость, используя соотношение 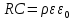. Во многих случаях такая методика оказывается предпочтительной.Теоретические вопросы: Вопрос № 17: Выведите формулу для расчета сопротивления утечки цилиндрического конденсатора. 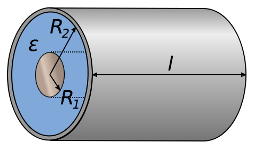 Воспользуемся законом Ома в интегральной форме: 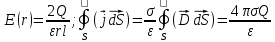 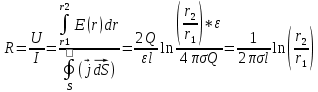 Где 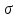 – удельное сопротивление диэлектрикаВопрос №20: Как можно рассчитать сопротивление проводника, зная его удельное сопротивление 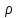и геометрические размеры?Если проводник в форме цилиндра, то можно воспользоваться формулой: 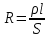Где S – площадь поперечного сечения проводника, l – его длина; Если проводник переменного сечения или в которых плотность тока не одинакова в любом сечении, то для таких проводников рассчитывают сопротивление, разбивая проводники (или проводящую среду) на множество элементов длиной dl с поперечным сечением S так, чтобы плотность тока в любой точке отдельного элемента была одинаковой. Сопротивление каждого отдельного элемента 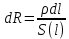где S – площади поперечного сечения проводника, а сопротивление проводника на участке от точки 1 до точки 2 равно 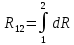Если такое разбиение невозможно или зависимость S(l) слишком сложна, используют подобие электрического поля в однородной проводящей среде с током электростатическому полю в диэлектрике при условии, что удельное сопротивление проводящей среды много больше удельного сопротивления материала электродов. Иначе говоря, распределение потенциала в проводящей среде с током окажется таким же, как и в диэлектрике (или вакууме), если, не меняя размеров и формы электродов, их взаимного расположения и разности потенциалов между ними, проводящую среду заменить диэлектрической. При этом выполняется соотношение 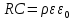где R – сопротивление утечки между двумя электродами в проводящей среде с удельным сопротивлением 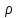; C – взаимная электроемкость электродов в среде с относительной диэлектрической проницаемостью 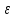. |