курсовая по тоэ в 1. Курсовая. Изобразим цепь с параметрами, исключив отсутствующие элементы
 Скачать 479.16 Kb. Скачать 479.16 Kb.
|
|
Задание 1. Вариант 1.3 Цепи постоянного тока  J Изобразим цепь с параметрами, исключив отсутствующие элементы     R1=7 Ом R1=7 Ом R2=12 Ом R2=12 Ом           E2 R5 R3=9 Ом        R4 R3 R2 R1 R4=10 Ом     E2 E1 R5=4 Ом       J=1 A J=1 AE1= 12 B E2=20 B E4= 12 B Rx= 3 Преобразуем её, применяя метод эквивалентного источника       У3 У1 E5=J*R5=1*4=4 B         I5 E5 R5         I3 I2 E2 R4 R1      R3 R2   I1    I4 E4 E1   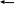    У2 Найдем количество контуров n с помощью количества p ветвей и количества q узлов p= 5 q=3 n=p-(q-1)=5-(3-1)=3 контура       У3 У1       E5 R5         К2 E2 R4 R1           К3 К1 R3 R2      E4 E1   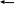   У2 Составляем СЛАУ: Сопротивление контуров R11=R1+R2=7+12= 19 Ом R22=R2+R3+R5=12+9+4= 25 Ом R33=R3+R4=9+10= 19 Ом Взаимный общий контур R12=R21= 12 Ом R23=R32= - 9 Ом R13=R31= 0 Ом Контурные ЭДС Ек1=Е1+Е2=14+20 = 34 В Ек2=Е2+Е5=20+4= 24 В Ек3=Е4=12 В Составляем матрицу: 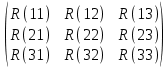 * * 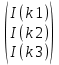 = = 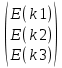 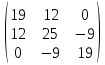 * * 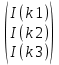 = = 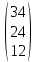 IK= 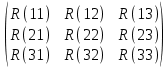 ^(-1) * ^(-1) * 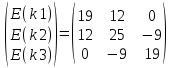 ^(-1) * ^(-1) * 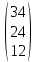 = = 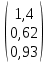 А АНаходим токи ветвей: I1= Ik1= 1,4 A I2= Ik1+Ik2= 1,4 + 0,62 = 2,02 A I3= Ik2 – Ik3= 0,62 – 0,93 = - 0,31 A I4= Ik3= 0,93 A I5= Ik2= 0,62 A Выполним проверку, согласно первому закону Кирхгофа: У1=I1+I5-I2= 1,4+0,62-2,02=0 A У2=I1+I4+I3-I2= 1,4+0,93-0,31-2,02=0 A У3=I3+I4-I5=-0,31+0,93-0,62=0 A Напряжение элементов (резисторов) U1= I1*R1= 1,4 * 7 = 9,8 B U2= I2*R2= 2,02*12 = 24,24 B U3= I3*R3= (-0,31) * 9 = -2,79 B U4= I4*R4= 0,93 * 10 = 9,3 B U5= I5*R5= 0,62 * 4 = 2,48 B Проверка напряжений по второму закону Кирхгофа: К1: Е2+Е1=U1+U2 => 14+20=9,8+24,24=> 34≈34,04 К2: Е2+Е5=U2+U3+U5 => 20+4=24,24-2,79+2,48=> 24≈23,93 К3: Е4=U4-U3 => 12=9,3-(-2,79) => 12≈12,09 Мощность элементов и их баланс: Потребители (резисторы): Pr1=U1*I1=9,8*1,4=13,72 Вт Pr2=U2*I2=24,24*2,02=48,97 Вт Pr3=U3*I3=(-2,79)*(-0,31)=0,87 Вт Pr4=U4*I4=9,3*0,93=8,65 Вт Pr5=U5*I5=2,48*0,62=1,54 Вт Сумма мощностей потребителей равна: Pr= Pr1+ Pr2+ Pr3+ Pr4+ Pr5=13,72+48,97+0,87+8,65+1,54=73,75 Вт Генераторы (источники): Pе1=Е1*I1=14*1,4=19,6 Вт Pе2=Е2*I2=20*2,02=40,4 Вт Pе4=Е4*I4=12*0,93=11,16 Вт Pе5=Е5*I5=4*0,62=2,48 Вт Сумма мощностей источников равна: Pe= Pе1+ Pе2+ Pе4+ Pе5=19,6+40,4+11,16+2,48=73,64 Вт Возьмем узел У2 как базисный (заземленный): µ2=0, тогда       У3 У1       E5 R5         К2 E2 R4 R1           К3 К1 R3 R2      E4 E1      У2 Найдем собственные потенциалы узлов G11=1/R1+1/R2+1/R5=1/7+1/12+1/4=0,48 Ом-1 G33=1/R4+1/R3+1/R5=1/10+1/9+1/4=0,46 Ом-1 G12=G21=-1/R5=-0,25 Ом-1 -Iy1=E1/R1-E2/R2+E5/R5=14/7-20/12+4/4=1,3 A -Iy3=E4/R4-E5/R5=12/10-4/4=0,2 A Составляем матрицу: 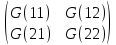 * *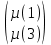 = =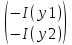 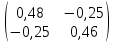 * *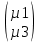 = =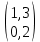 Отсюда µ1=4,3 B µ3=3,05 B Найдем токи ветвей в соответствии с узлами I1=(E1-µ1)/R1=(14-4,3)/7=1,39 A I2=(E2+µ1)/R2=(20+4,3)/12=2,025 A I3=-µ3/R3=-3,05/9=-0,33 A I4=(E4-µ3)/R4=(12-3,05)/10=0,92 A I5= (µ3-µ1+E5)/R5=(3,05-4,3+4)/4=0,64 A Проверим по первому закону Кирхгофа: J1: I1+I5-I2=1,39+0,64-2,025≈0 J2: I1+I3+I4-I2=1,39-0,33+0,92-2,025≈0 J3: I3+I4-I5=-0,33+0,92-0,64≈0 Метод эквивалентного источника относительно R3        I5 У3 У1        E5 R5            b I2 К2 E2 R4 R1            К3 К1 R2      a I3       I1 I4 E4 E1        У2 Преобразуем цепь в эквивалентную методом прямой свертки:                                   b a E4 E2 E5 E1 R1 R2 R5 R4 Меняем Е1, R1, E2 и R2 на эквивалентную схему (меняем источник напряжения на источник тока): J1=E1/R1=14/7=2 A J2=E2/R2=20/12=1,7 A                                       J1 J2 R2 R1 R5 E5 E4 R4 b a Складываем источники тока и резисторы и создаем эквивалентную схему, заменяя источник тока на источник напряжения: J12=J1-J2=2-1,7=0,3 A R12=R1*R2/(R1+R2)=12*7/(12+7)=4,42 Oм Е12=R12*J12=4,42*0,3=1,33 В        E5                     b a E4 R4 E12 R12 R5 Складываем источники напряжения и резисторы: R125=R12+R5=4,42+4=8,42 Ом Е125=Е5-Е12=4-1,33=2,67 В                  b a E4 R4   R125    E125 Преобразуем источники ЭДС в источники тока J125=E125/R125=2,67/8,42=0,32 A J4=E4/R4=12/10=1,2 A               b a            R125 R4 J4 J125  Складываем источники тока и резисторы J1245=J125+J4=0,32+1,2=1,52 A R1245=R125*R4/(R125+R4)=8,42*10/(8,42+10)=4,57 Ом             b a       J1245 R1245 Заменяем источник тока на ЭДС Е1245=R1245*J1245=4,57*1,52=6,95 B        R1245     E1245 R3 Для расчета ток через резистор воспользуемся законом Кирхгофа для полной цепи I3=E1245/(R3+R1245)=6,95/(4,75+9)=0,34 A Сила тока, полученная при расчете, соответствует значению при использовании метода контурных токов и метода узловых потенциалов. Таблица токов, напряжений и мощности. |
