Практическая. ПР№2. Изучение математических моделей нелинейных динамических систем
 Скачать 203.25 Kb. Скачать 203.25 Kb.
|
|
Практическая работа № 2. Тема:Изучение математических моделей нелинейных динамических систем. Динамические системы. Динамическая система – это объект или процесс, который характеризуется своим состоянием как совокупностью характеристик в некоторые моменты времени, и определен закон эволюции состояния динамической системы во времени. Примеры динамических систем можно найти в физике, биологии, химии, информатике, экономике, социуме. Закон эволюции состояния динамической системы во времени может быть задан например, системой дифференциальных уравнений. Математическое моделирование нелинейных динамических систем является междисциплинарным инструментом исследования разнообразных процессов в природе и обществе. При этом реализуется единый методологический подход, позволяющий на основе объективных законов анализировать движение разнообразных динамических систем различного уровня сложности – от механических до социальных. Первоначально основные математические модели динамических систем были разработаны для технических и естественнонаучных приложений. Впоследствии выяснилось, что аналогичные эффекты, закономерности поведения присущи и другим системам – метеорологическим, экономическим, финансовым, социальным. Сложные хозяйственные системы охватывают практически все перечисленные направления. Классификации динамических систем.Рассмотрим различные виды динамических систем и соответствующих им математических моделей на основе математического аппарата теории обыкновенных дифференциальных уравнений. Существуют различные классификации процессов в динамических системах. Рассмотрим один из возможных вариантов. 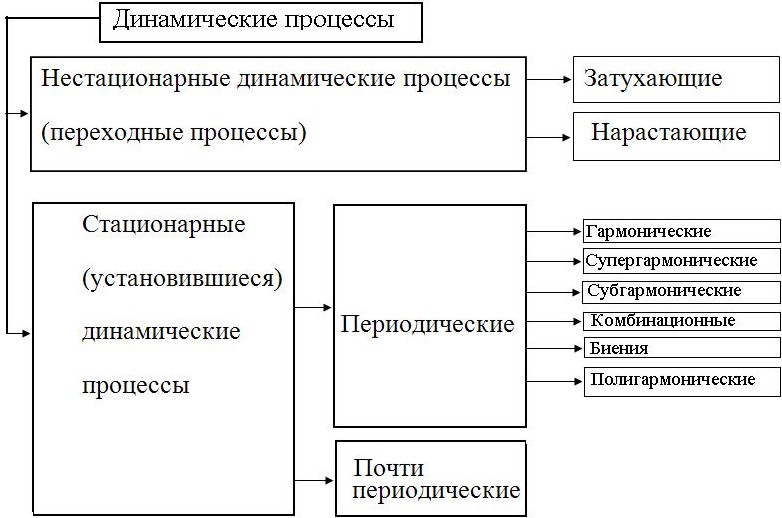 Рисунок 1 – Классификация динамических процессов Детерминированными называют модели, в которых все переменные детерминированы; функции являются детерминированными функциями своих аргументов. Естественно ожидать, что решения в таких моделях будут детерминированными функциями. Во многих случаях это так, но решения некоторых существенно нелинейных систем в определенных условиях ведут себя как случайные функции. Стохастическими называют модели, в которых внешние воздействия или параметры системы являются случайными функциями. Динамические модели по числу переменных, включаемых в динамический процесс, разделяются на системы с одной степенью свободы, системы с несколькими степенями свободы и системы с бесконечным числом степеней свободы (континуальные). Одна из возможных классификаций моделей приведена ниже. 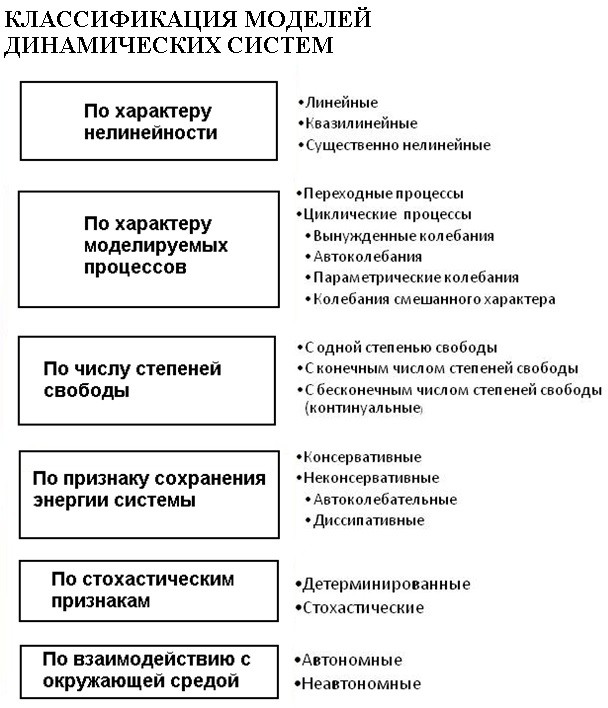 Рассмотрим подробнее основные разновидности динамических систем. Автономные и неавтономные системы. Линейные и нелинейные модели динамических процессов разделяются на автономные и неавтономные. В автономных системах внешние воздействия зависят только от состояния системы, и в дифференциальное уравнение движения время tявным образом не входит. В дифференциальные уравнения движения неавтономных систем время tвходит явно, в них присутствуют функции времени t. Понятие автономности не совпадает с понятием замкнутости (изолированности) системы. Последнее соответствует отсутствию внешних воздействий. Автономная система может быть незамкнутой (пример – системы, в которых возникают автоколебания). Замкнутая система может быть неавтономной (при действии парных внешних воздействия, заданных в виде явных функций времени t). Автономные системы могут быть консервативными и неконсервативными. К неконсервативным системам относятся диссипативные и автоколебательные. Консервативными системами называются автономные системы, в которых полная энергия (для механических систем) или ее аналог (для других систем) постоянны во времени. Диссипативными называют автономные системы, в которых присутствуют диссипативные силы (силы сопротивления движению) или их аналоги. Неавтономные системы характеризуются тем, что в них присутствуют слагаемые, явным образом зависящие от времени t. Обычно эти слагаемые соответствуют внешним воздействиям. Линейные и нелинейные модели динамических систем. Первые математические модели динамических систем базировались на основе линейных дифференциальных уравнений. Линейные модели позволили получить первые принципиальные результаты (эффекты резонанса при вынужденных колебаниях, взаимодействия различных мод колебаний в многомерных динамических системах и др.), но эти модели достаточно быстро достигли предела своей применимости. Отмечается принципиальное несоответствие некоторых результатов, получаемых с помощью линейных моделей, результатам натурных экспериментов даже для простейших механических и электромеханических систем (например, возможность существования неограниченно возрастающих решений в математической модели). Следующим этапом развития динамического моделирования можно считать учет нелинейных зависимостей в математической модели. Первоначально нелинейные слагаемые принимались как малые величины по сравнению с линейными составляющими моделей. Такие системы получили название квазилинейных, и для их анализа были развиты асимптотические методы. Результаты, полученные с помощью асимптотических методов, позволили обнаружить много новых по сравнению с линейными моделями эффектов. Среди этих результатов можно выделить возможность существования нескольких устойчивых и неустойчивых динамических режимов при одинаковых параметрах динамической системы и внешнего возмущения, неизохронность собственных колебаний, то есть зависимость частоты собственных колебаний от их амплитуды, существование субгармонических и ультрагармонических решений, бифуркации решений, существование устойчивых автоколебаний с ограниченной амплитудой, эффекты синхронизации и захватывания в динамических системах. Впоследствии, с развитием вычислительной техники, стало возможным строить существенно нелинейные динамические модели. |
