лб. Линеаризация динамических систем
 Скачать 148.6 Kb. Скачать 148.6 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра КСУ отчет по лабораторной работе №1 по дисциплине «Математическое моделирование объектов и систем управления» Тема: «Линеаризация динамических систем» Вариант 1
Санкт-Петербург 2021 Цель работы: освоить аналитические и машинные способы линеаризации динамических систем, проанализировать и оценить свойства динамических систем по линеаризованным моделям. Выполнения работы 1. Построить модель динамической системы в среде SIMULINK в соответствии с исходными данными. Исходная СНДУ: 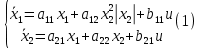 По исходной СНДУ (1) была построена модель динамической системы в среде SIMULINK, рисунок 1. 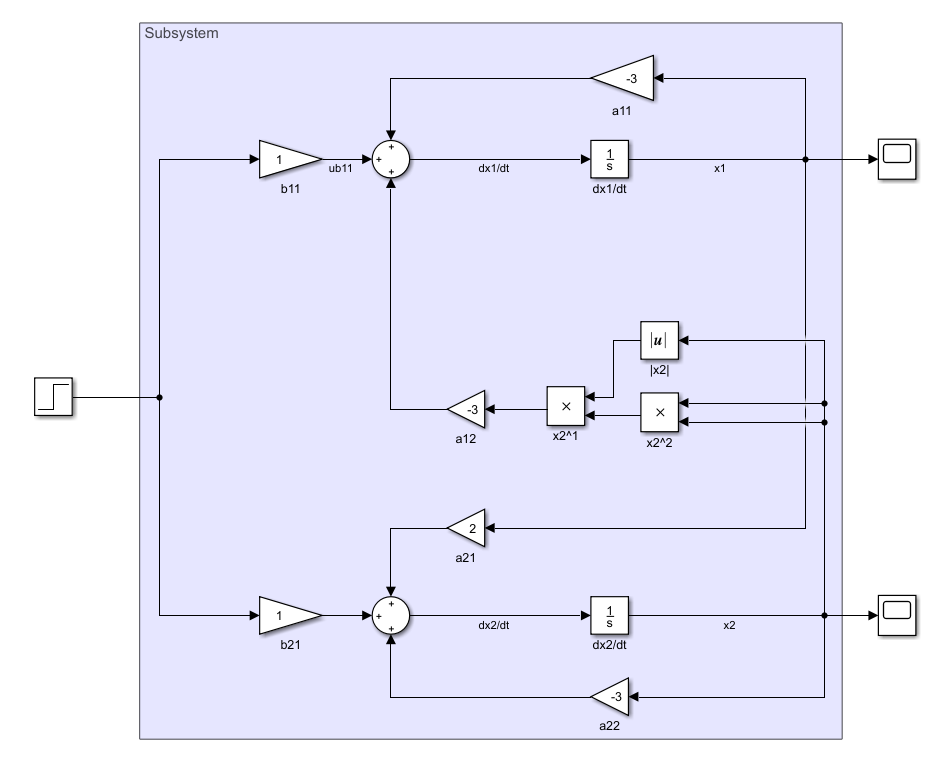 Рис.1 Модель динамической системы в среде SIMULINK 2. Подобрать коэффициенты модели таким образом, чтобы система оказалась устойчивой. Путём моделирования были подобранны коэффициенты: a11 = -3; a12 = -3; a21 = 2; a22 = -3; b11 = 1; b21 = 1; Результаты моделирования: 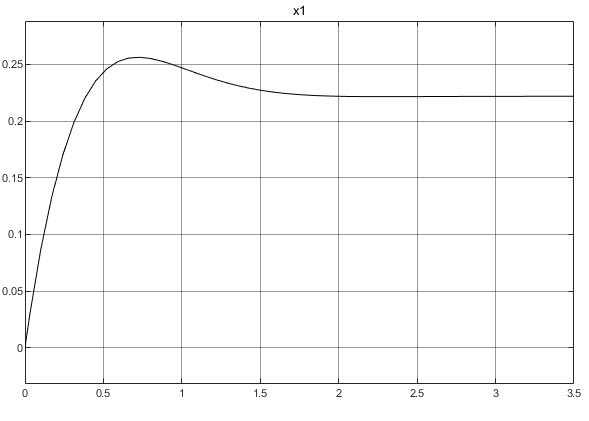 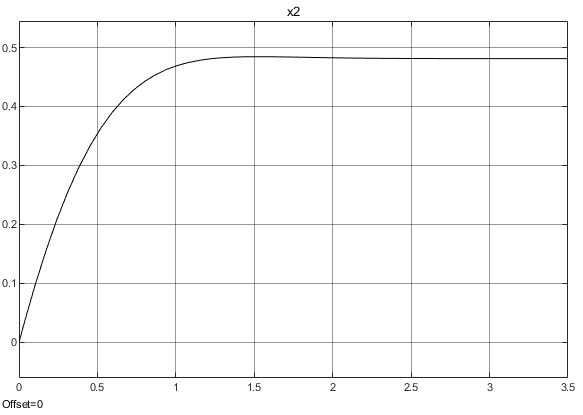 Рис.2 Результаты моделирования при единичном входном ступенчатом воздействии x1, x2, при u = 1. Как видно из установившихся переходных процессов рисунка 2, система оказалось устойчивой. 3. Создать модель, аналогичную найденной, используя в качестве входных и выходных сигналов порты входа-выхода. 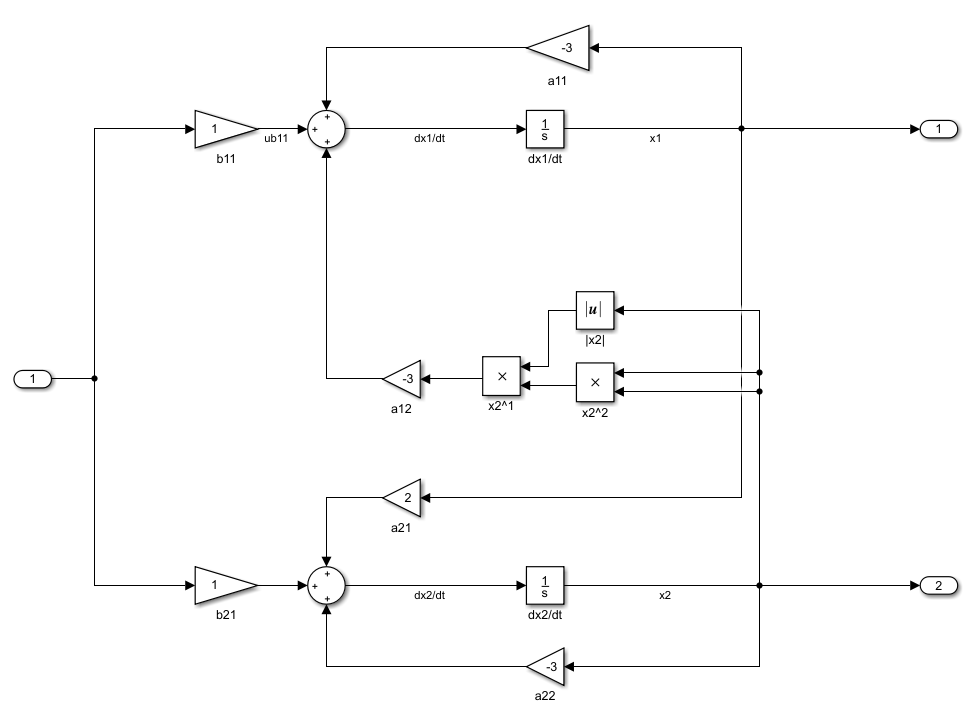 Рис.3 Модель динамической системы в среде SIMULINK с входными и выходными сигналами в виде портов входа-выхода 4. Определить точку равновесия, используя функцию TRIM с тремя аргументами. С помощью функции «TRIM» определим точку равновесия системы: [x,u,y] = trim('Lab11', [0; 0], 1) Где «Lab11» – модель, изображенная на рис.3. Полученные точки равновесия:  Рис.4 Результат выполнения функции «TRIM» без фиксирования значений 5. Проверить корректность работы функции TRIM моделированием. По графикам модели (см. рисунок 2) установившееся значения переменных состояния: х1 = 0,222; х2 = 0,481 (2) Результаты моделирования с помощью SIMULINK и функции TRIM не совпадают. Это связано с тем, что функция «TRIM» ищет ближайшую из существующих точек равновесия, если не задать в ней фиксированное начальное значение входа u. Используем функцию «TRIM» повторно, но с фиксированным входным воздействием: [xs, us, ys] = trim ('Lab11', [0; 0], 1, [0; 0], [], [1], []); Результат выполнения программы представлен на рисунке 5. 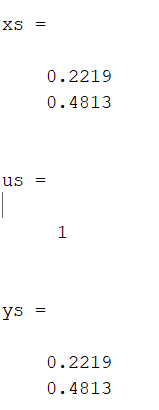 Рис.5 Результат выполнения функции «TRIM» с фиксированными значениями. Значения полученной точки равновесия с помощью функции «TRIM» c зафиксированным входным значением совпадает с установившимися значениями модели SIMULINK (2). 6. Найти линеаризованную модель системы аналитическим и машинным способом. Проверить модели на соответствие. Найдём линеаризованную модель аналитическим способом: За выходы системы принимаем х1, х2, то есть: 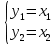 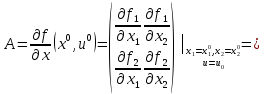 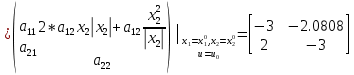 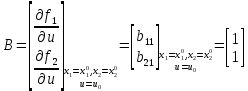 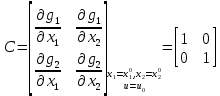 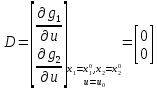 Линеаризованная система, полученная аналитическим способом, имеет следующий вид: 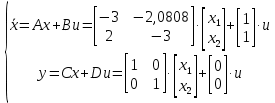 С помощью функции «linmod» получим матрицы СЛДУ, фрагмент исполняющего кода: xs = [0.2219; 0.4813]; us = [1]; [A1, B1, C1, D1] = linmod ('Lab11', xs, us); Результат выполнения программы:  Рис.6 Результат выполнения функции «linmod» Модели, полученные аналитическим и машинным способом, совпадают. 7. Определить точку равновесия, соответствующую заданным в п. 4 входным воздействиям. Найти линеаризованную модель для новой точки равновесия. Найдём решение СНДУ при u=1 (точки равновесия системы с фиксированным входным воздействием) с помощью функции «SOLVE». Код программы: syms x1 x2 u = 1; f1=a11*x1+a12*abs(x2)*x2*x2 + b11*u; f2=a21*x1+a22*x2+b21*u; vars = [x1 x2]; eqns = [f1, f2]; [solX1, solX2] = solve(eqns, vars); s1 = double(solX1); s2 = double(solX2); x_1 = (s1(1)) x_2 = (s2(1)) x_3 = (s1(2)) x_4 = (s2(2)) % % Линеаризованные значения по полученным значениям СНДУ: [A, B, C, D] = linmod('Lab11', [x_1; x_2], 1) С помощью функции «SOLVE», были получены две точки равновесия представленные на рисунке 7. Точка 0.2219; 0.4813 совпадает с полученной ранее, в отличии от точки -2.6623; -1.4416. 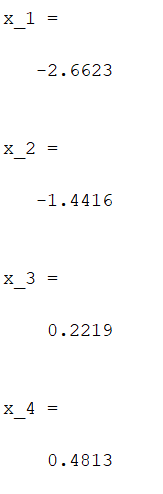 Рис.7 Точки равновесия Матрицы СЛДУ для новой точки равновесия -2.6623; -1.4416:  Рис.8 Линеаризованная модель для новой точки равновесия. 8. Сравнить собственные числа моделей, найденных в п. 6 и п. 7. Найдём собственные числа для линеаризованной модели полученной с помощью функции «TRIM» и функции «SOLVE»:  Рис.9 Линеаризованная модель для новой точки равновесия. В первой точки действительная часть собственных чисел отрицательная, что говорит об устойчивости системы, в отличии от положения во второй, что говорит об неустойчивости системы. Вывод. В данной лабораторной работе были найдены точки равновесия системы с помощью функции «TRIM» и «SOLVE». Для обработки SIMULINK объекта, использовалась функция «TRIM» с тремя аргументами, полученная точка равновесия не удовлетворяла т.к. не совпадала с найденной в SIMULINK модели. С помощью функци «TRIM» с фиксированным значением по входу была найдена точка равновесия совпадающая с найденной в SIMULINK модели. С помощью функция «SOLVE» были найдены две точки равновесия, одна из которых совпала с найденной в модели SIMULINK, для несовпадающей же точки будем искать линеаризованную модель и сравнивать с полученной в «TRIM» с фиксированным значением. Нашли линеаризованные модели СНДУ аналитическим и машинным способом. После произведены сравнения собственных чисел моделей, для точки полученной с помощью функции «TRIM» вещественная часть собственных чисел лежит в левой полуплоскости, что говорит об устойчивости системы. Для другой точки, найденной с помощью функции «SOLVE», вещественная часть одного из собственных чисел лежит в правой полуплоскости, что говорит о неустойчивости системы в этой точке. Код программы: clc; [x, u, y] = trim('Lab11', [0; 0], 1); [xs, us, ys] = trim('Lab11', [0; 0], 1, [0; 0], [], [1], []); [A1, B1, C1, D1] = linmod('Lab11', xs, us); b11 = 1; b21 = 1; a11 = -3; a12 = -3; a21 = 2; a22 = -3; [x, u, y] = trim('Lab11', [0; 0], 1); [xs, us, ys] = trim('Lab11', [0; 0], 1, [0; 0], [], [1], []) [A1, B1, C1, D1] = linmod('Lab11', xs, us); b11 = 1; b21 = 1; a11 = -3; a12 = -3; a21 = 2; a22 = -3; syms x1 x2 u = 1; f1=a11*x1+a12*abs(x2)*x2*x2 + b11*u; f2=a21*x1+a22*x2+b21*u; vars = [x1 x2]; eqns = [f1, f2]; [solX1, solX2] = solve(eqns, vars); s1 = double(solX1); s2 = double(solX2); x_1 = (s1(1)) x_2 = (s2(1)) x_3 = (s1(2)) x_4 = (s2(2)) % % Линеаризованные значения по полученным значениям СНДУ: [A, B, C, D] = linmod('Lab11', [x_1; x_2], 1) % % % Собственные значений линеаризованных значений: forTrim = eig(A1) forSolve = eig(A) |
