Моделирование. Мат.мод.Ан.И ИМ.. Комбинированные модели (Асхемы) Комбинированные модели
 Скачать 1.26 Mb.
|
|
Комбинированные модели (А-схемы) Комбинированные модели базируются на понятии агрегативной системы (англ.aggregate system) – формальная схема общего вида, далее А – схема. Подход предложен Н.П. Бусленко. При агрегативном описании сложный объект разбивается на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие их взаимодействие. Система делится на части (агрегаты) таким образом, чтобы при моделировании они были удобными для математических описании. В результате декомпозиции сложная система представляется многоуровневой конструкцией их взаимосвязанных элементов, объеденные в подсистемы различных уровней. Под агрегатом понимается любой объект, определяемый упорядоченной совокупностью множеств  и случайных операторов . Множества:  - моменты времени  ;  - входные сигналы -  ;  - выходные сигналы ; состояние агрегата  . Переход агрегата из состояния  в состояние происходит за малый интервал времени, т.е. имеет место скачек . Переходы агрегата из в  определяется собственными параметрами  и входными сигналами .В начальный момент времени  состояние  имеют значение , т.е.  задаваемое законом распределения . - случайный оператор, которым описывают процесс функционирования агрегата в случае воздействия входного сигнала в момент времени . Состояние будет определено в форме  - случайный оператор определения состояния агрегата в интервале времени  если нет поступления не одного сигнала. Состояние агрегата определяется соотношением Совокупность и рассматривают как оператор переходов агрегатов в новое состояние. - случайный оператор, представляющий собой частный случай оператора используется для описания скачков состояния в особые моменты времени  : Переход агрегата из одного состояния в другое (операторы и ) состоит из скачков . Моменты скачков называют особыми моментами времени . - оператор выходов Здесь в подмножестве  выделяют подмножество  ,что если  достигнет , то это состояние является моментом выдачи выходного сигнала –  Входные сообщения или  – сообщения – последовательность входных сигналов, расположенных в порядке их поступления в А – схему.Выходное сообщение или – сообщение – последовательность выходных сигналов, упорядоченных относительно времени выдачи.Агрегативная система Существует класс сложных систем, которые не могут быть формализованы в виде математической схемы одного агрегата. Формируют конструкцию из отдельных агрегатов –  , которую и называют агрегативной системой – А – схемой. Необходимо математическое описание, как отдельных агрегатов, так и связей между ними.Агрегат  в системе имеет:-входные контакты, куда поступает совокупность входных сигналов  -выходные контакты, с которых снимается совокупность элементарных сигналов  .У агрегата  входных и  выходных контактов.Сигналы между агрегатами в А – схеме передаются по элементарному каналам. При этом к входному контакту можно присоединить только один канал, а от выходного контакта может направляться несколько элементарных каналов. Внешняя среда представляется фиктивным  агрегатом, вход которого содержит  входных контактов , а выход –  выходных контактов . Сигнал А – схемы, выдаваемый во внешнюю среду воспринимается как входной, а сигнал в А – схемы как выходной. А – схема характеризуется: Множеством входных контактов  , обозначим Множеством выходных контактов  , обозначим  .Множества и являются математической моделью элемента , используемого для формального описания сопряжения с прочим элементами А – схемы и внешней средой Входному контакту 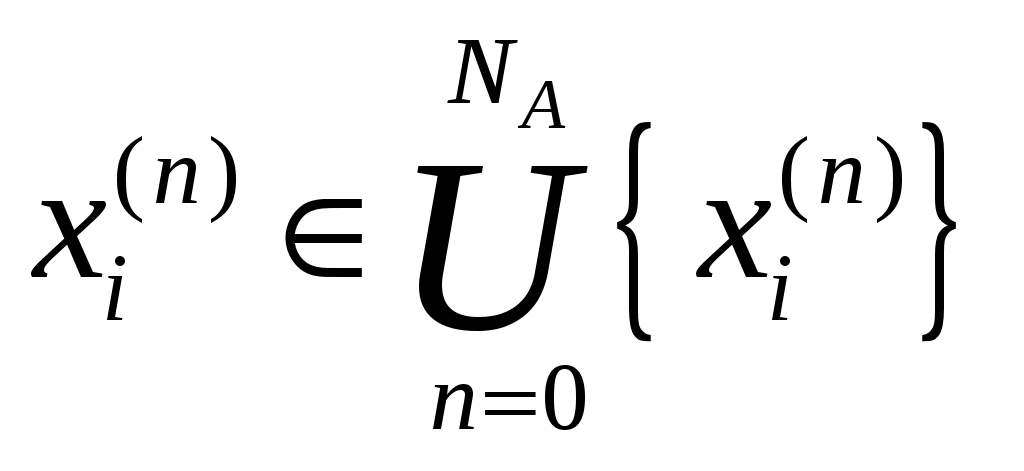 соответствует не более чем один выходной контакт 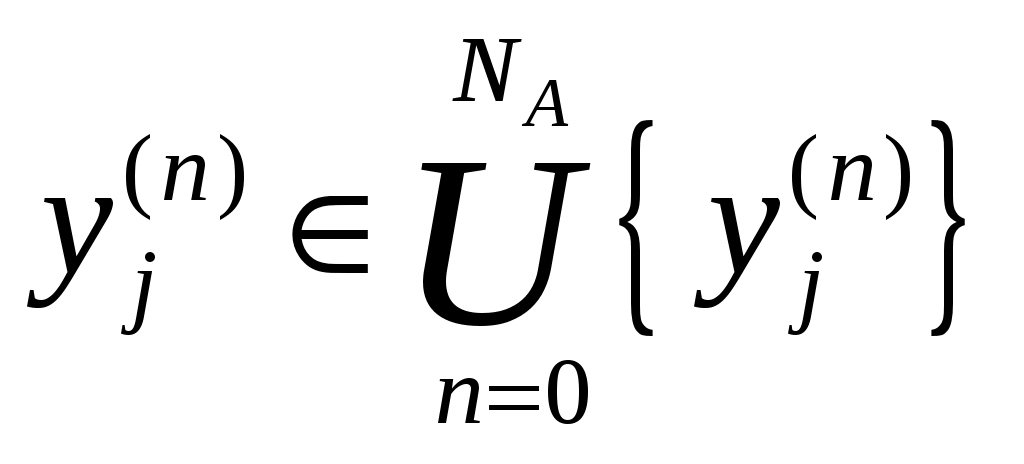 ,где  -множество входных контактов всех элементов А – схемы и внешней среды  - множество выходных контактов всех элементов А – схемы и внешней среды , с которыми она связана элементарным каналом Можно ввести однозначный оператор  , сопоставляющий входному контакту выходной сигнал , связанный с ним элементарным каналом. Оператор не определен, если в А – схеме к контакту не подключен элементарный канал. Совокупность множеств ,  и оператор образуют схему сопряжения элементов в систему  .Рассмотрим пример оператора в виде таб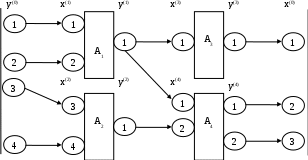лицы для А – схемы, показанной на рис. 4.5Вариант №1  А0 Оператор сопряжения
Рис.4.5. Структура агрегативной системы. Рассмотрение связей в направлении противоположном стрелкам. Ограничения в структуре сопряжения агрегатов: Каждый элементарный канал, передающий сигналы во внешнюю среду начинался в одном из выходных контактов одного из агрегатов системы Каждый элементарный канал, передающий сигнал из внешней среды заканчивался на одном из входных контактов А – схемы  Сигналы от одного агрегата к другому передаются без устройств, способных отсеивать сигнал по каким – либо признакам Сигналы между агрегатами передаются мгновенно без искажения и перекодирования, изменяющего структуру сигнала.Осуществляется согласование функционирования агрегатов по времени  Частный случай – кусочно – линейные агрегаты, для которых результаты моделирования могут быть получены аналитическим методом. В более сложных случаях прибегают к имитационному методу. 4.5 Аналитические математические модели Классификация аналитических моделей В аналитических математических моделях результат можно вычислить, т.е. совокупность соотношений может быть решена относительно исходных величин. В связи с целями моделирования различают модели дискрептивные, оптимизационные, многофакторные. Дискрептивные модели имеют цели получения описаний процессов функционирования систем, т.е. характеристик при некоторых воздействиях, параметрах и начальных условиях. В оптимизационных моделях решают задачи выбора оптимального варианта из некоторого их числа. При этом задаются критерии оптимальности, служащие мерилом при выборе варианта. Многофакторные модели связаны с учетом большого числа факторов, формирующих результат. Структура аналитических моделей определяется типом математических соотношений и характером рассматриваемых явлений. В целом можно выделить следующие разновидности моделей: конечных автоматов; математической физики; сетевые; теории графов; массового обслуживания; теории игр; математического программирования. В связи с видом соотношения модели математического программирования делят на группы: линейные, не линейные, динамические, диаметрические, дискретные, стохастические, эвристические. Структура аналитических моделей (АМ) показана на рис 5.6. 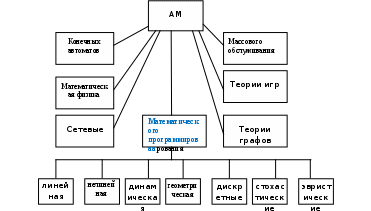 | ||||||||||||||||||||||||||||||||||