Моделирование. Мат.мод.Ан.И ИМ.. Комбинированные модели (Асхемы) Комбинированные модели
 Скачать 1.26 Mb.
|
|
Аналитические математические модели В АММ результат можно вычислить, т.е. совокупность соотношении может быть решена относительно исходных величин. В связи с целями моделирования различают модели дискрективные, оптимизационные, многофакторные. Дискриктивные (относительные) модели имеют целью описание процессов функционирования систем в форме характеристик. В оптимизационных моделях решают задачи выбора оптимального варианта из некоторого их числа при этом задают некоторые критерии оптимальности, которые и служат мерилом оптимальности. Многофакторные модели связаны с учетом большого числа факторов, формирующих результат. Структура АММ определяется типом (видом) математической схемы (математических соотношений) и характером рассматриваемых явлений. Выше уже рассматривались ряд математических схем, которые и определяют по большей части АММ. Классификационная схема АММ приведена на рис.4 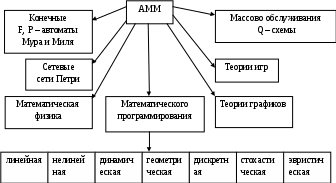 Выделяют следующие классы моделей в связи с их математическими схемами: конечных автоматов (F, P – автоматы Мура и Миля), сетевые (сети Петри), математической физики, массово обслуживания (Q – схемы), теории игр, теории графиков, а также математического программирования с широким диапазоном математических схем. Заметим, что приведенные разновидности математических схем не исчерпывают всей палитры математических методов, но чаще всего используются в аналитических схемах, а также в ряде случаев и в имитационных моделях. Модели математического программирования Представление задачи моделирования:  - некоторая целевая функция, для СТС это может быть показатель эффективности,  и  управляемые и неуправляемые векторы переменных величин, задача найти максимум и минимум или некоторый оптимум  при ограничениях . Здесь  - есть функция i-го ресурса, а  - его величина. Нахождение оптимального решения зависит от вида и структуры функций: целевой и ограничений .Линейное программирование – функции и  линейны относительно вектора  . Это, как правило, система линейных алгебраических уравнений.Нелинейное программирование – функции и нелинейны относительно вектора .Динамическое программирование – функция имеет определенную структуру: аддитивна относительно , т.е.  , мультипликативна относительно , т.е.  .Геометрическое программирование – функции  и  представляются функциями полиномами вида: ,где – некоторые коэффициентыСтохастическое программирование – – неуправляемая величина. Задача состоит в получении  при ограничениях . Здесь – математическое ожидание по  . Возможные вероятностные ограничения:  или  – вероятности выполнения условий  .Дискретное программирование – на одну из управляемых переменных наложено условие дискретности (целочисленности, к примеру,  – целое число)Эвристическое программирование – точные оптимум целевой функции алгоритмическим путем найти невозможно из-за большого числа вариантов. В этом случае отыскивают удовлетворительное решение путем выдвижения эвристик (догадок) в этом случае сокращается число просматриваемых вариантов.Модели математического программирования относятся к числу оптимизационных. Используются в моделях оптимизации. Применимы для детерминированных систем, где влияние случайных факторов несущественно отражается на результате функционирования системы. Имитационное моделирование Общие сведения по имитационному моделированию Под термином “Имитационное моделирование следует понимать такие математические модели (ММ) с помощью которых нельзя заранее вычислить или предсказать результат.” Для предсказания результата необходим эксперимент – имитация на модели при заданных исходных данных. Имитация представляет собой численный метод проведения на ЭВМ экспериментов с ММ, описывающих поведение системы в течении заданного или формируемого периода времени. Другие определения ИММ: ИМ – это алгоритм, программа описывающая процесс функционирования СТС, реализуема на компьютере. ИМ применяют для систем, которые нельзя описать аналитическими формулами, уравнениями. Много случайных факторов, неизвестны законы, управляющие поведением СТС. Структура и характерные понятия для ИМ Структура ИМ в общем случае одинакова с рассмотренной ранее формой ММ. В обобщенном виде можно представить схемой  В структуре обозначено:  - результат действия системы,  - управляемые и неуправляемые переменные и параметры,  - функциональная зависимость.Понятия характерные для ИМ: Компоненты – составные части системы; Переменные – экзогенные – входные порождаются вне системы, эндогенные – возникающие в системе – это переменные состояния и выходные; Функциональные зависимости – описывают поведение параметров и переменных в компонентах Ограничения – пределы изменения параметров и переменных Целевая функция – отображение целей и задач системы Критерии – мерило оценки, правило проверки Функция критерия – процесс манипуляции с моделью с целью оптимизации заданного критерия Основа ИММ моделирующии алгоритм МА, воспроизводящий функционирование оригинала, МА представляется комбинацией ряда подалгоритмов в основном трех типов: объединение подпроцессов в процессе согласования отдельных подалгоритмов. Структура №1 показана на рис.4 . на вход ИМ поступает набор чисел, отображающих процесс с заданной корреляционной функцией. По реализации выходного сигнала можно оценить корреляционную функцию выходного сигнала. С  труктура МАКлассификация ИМ Классификационная схема приведена на рис.4.. 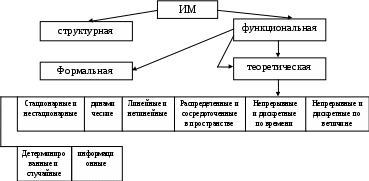 Стационарные и нестационарные ИМ определяются видом моделируемого случайного процесса. Частный случай статическая модель при установившихся (равновесных) режимах. Динамические модели задают дифференциальные уравнениями Линейные и нелинейные модели рассматривают по отношению к входным сигналам: линейная – комбинации сигналов на входе и выходе модели линейны; нелинейная – два подкласса моделей по виду уравнений – алгебраические и трансцендентные. Модели непрерывные и дискретные по времени и величинам соответствуют процессам с непрерывными или дискретными значением времени или величин. Детерминированные или случайные модели описываются детерминированными или случайными функциями. Информационные модели – определяют скорость, содержание и формат подготовки потока информации. |