Моделирование. Мат.мод.Ан.И ИМ.. Комбинированные модели (Асхемы) Комбинированные модели

• Название: Комбинированные модели (Асхемы) Комбинированные модели
• Анкор: Моделирование
• Дата: 05.10.2022
• Размер: 1.26 Mb.
• Имя файла: Мат.мод.Ан.И ИМ..doc
• Тип: Документы; #714950
• страница: 3 из 5

Для ИМ характерны понятия:

• 
  компоненты – составные части, которые при объединении образуют систему – это элементы и подсистемы;
  
• 
  переменные – рассматриваются двух типов:
  

экзогенные – входные, порождаются вне системы, являются результатом внешних причин, независимые;

эндогенные – возникают в системе в результате действия внутренних причин – это переменные состояния или выходные переменные;

• 
  функциональные зависимости – описывают поведение параметров и переменных в пределах компонент или выражают соотношения между ними;
  
• 
  ограничения – устанавливают пределы изменения переменных и параметров, могут быть искусственными – вводящимися разработчиками и накладываемые системой вследствие присущих ей свойств;
  
• 
  целевая функция – точное отображение целей и задач системы и правила оценки их выполнения;
  
• 
  критерий – мерило оценки, правило или вид проверки, при помощи которого составляется правильное суждение о чем-либо;
  
• 
  функция критерия – процесс манипуляции с моделью, направленный на оптимизацию или удовлетворение заданного критерия.
  

Основу ИМ составляет моделирующий алгоритм, приближенно воспроизводящий функционирование оригинала. Имитируется, как правило, элементарные явления, составляющие процесс с сохранением логической структуры и последовательности протекания во времени.

Моделирующий алгоритм представляется комбинацией ряда подалгоритмов, из которых можно выделить три основных типа: моделирование элементарных процессов; объединение подпроцессов в процесс; согласование отдельных подалгоритмов. Структура комбинаций подалгоритмов показана на рис 4.9.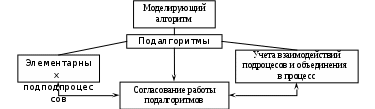

Рис. 4.9. Структура моделирующего алгоритма ИМ

В отличие от аналитической модели в ИМ на входе задают набор чисел, отображающих процесс с заданной корреляционной функцией. В ходе моделирования получают реализацию выходного процесса, по которой можно оценить корреляционную функцию выходного сигнала.

Классификация ИМ по основным признакам показана ниже. Основным типом ИМ является функциональная теоретическая. Вид этих моделей определяется классом случайного процесса, которым описывается функционирование системы. На схеме рис. 4.10. показаны виды ИМ, а ниже приведены их характеристика.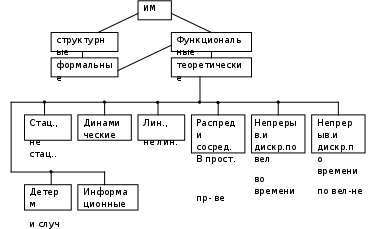



Рис.4.10. Классификационная схема ИМ

Стационарные и нестационарные ИМопределяются видом моделируемого случайного процесса. В стационарной ИМ имеет место сдвиг по времени входного и выходного сигналов, при этом форма не изменяется, а оператор системы не меняет структуры и свойств во времени. В случае нестационарной ИМ выходной сигнал изменяет форму, меняются также структура и свойства во времени. Частным случаем стационарной модели является статическая модель, описывающая связи между переменными процесса в установившихся режимах (равновесное состояние, к примеру, тепловые балансы, медленно протекающие процессы). Стационарные ИМ состоят из дифференциальных уравнений, а статические – из алгебраических.

Динамические модели задаются дифференциальными уравнениями (к примеру, LC – контур или маятник, см. выше). Состояние системы можно наблюдать в различные моменты времени.

Линейные и нелинейные модели рассматриваются по отношению к входным сигналам. Модель и система называются линейными, если выполняется принцип суперпозиции: линейной комбинации произвольных входных сигналов соответствует линейная комбинация на выходе системы.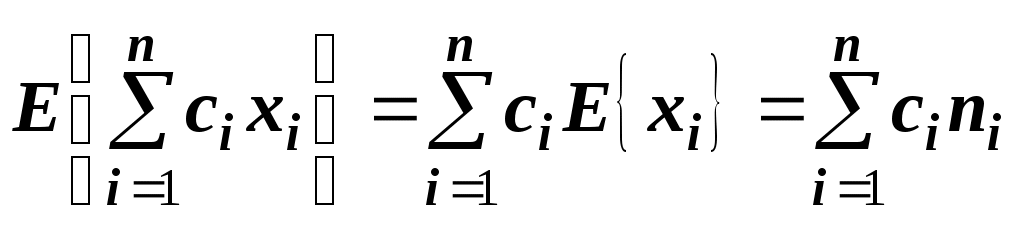



Нелинейные модели делят на два подкласса по виду уравнений: алгебраические и трансцендентные.

Модели распределенные и сосредоточенные в пространстве – моделируемый процесс может быть распределен или сосредоточен в пространстве.

Модели непрерывные и дискретные во времени: непрерывная – переменные определяются для любого времени – y=E(t), где t может принимать любые значения; дискретная – переменные получают значения только в определенные моменты времени - y=f(kΔt), k=0,1,2…

Непрерывные и дискретные по величине модели – соответствуют процессам с непрерывными и дискретными значениями.

Детерминированные и случайные модели, имеют математические описания детерминированными или случайными функциями.

Информационные модели применяют при моделировании сложных устройств и комплексов типа ЭВМ, определяют содержание, формат и скорость подготовки потока информации.

4.8 Механизм имитации функционирования СТС на ЭВМ

Модельное время

Пример. Объектом имитации является обработка i-ой детали на нескольких станках. Каждый j-ый станок выполняет набор операций – представляет собой функциональное действие . Обработку множества деталей можно представить как сложную систему.

В результате выполнения 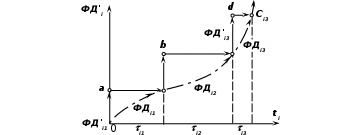происходит некоторое событие . Любое связано с компонентой и выполняется за интервал времени . Для каждой можно рассматривать свое локальное время . В сложной системе все выполняются одновременно, характер их изменения различен и определяется последовательностью временных интервалов .

В ИМ апроксимируется упрощенным , что определяет степень детализации сложной системы. Таким образом, в ИМ представляется парой - , которая выполняется следующим образом: вначале реализуется при неизменном , а затем отображается изменение на величину , инициируя появление события . Представление об имитации функционирования компоненты можно получить из графика рис.4.11.



Рис. 4.11. График функционирования компоненты СТС

В ИМ в общем случае описывается некоторым алгоритмом , и происходит изменение на величину . Таким образом, любая ИМ описывается набором «молекул» (ячеек), каждая из которых содержит и оператор модификации - , осуществляющего изменение на . Пару - называют активностью и обозначают . Реализация активности в ИМ приводит к появлению события .

Если в ЭВМ имитировать поведение только одной компоненты, то активности можно было бы выполнять строго последовательно, и дело свелось бы к пересчету временной координаты . Реальные сложные системы состоят из нескольких компонент и все – функционируют одновременно. ЭВМ в каждый момент времени может реализовать алгоритм только одной компоненты. Для имитации параллельных событий реальной системы вводят глобальную переменную – модельное (системное) время – . С помощью организуется синхронизация всех событий и выполнение алгоритмов .

В ИМ используют три представления времени: реальное – работы системы , модельное – для синхронизации событий , машинное – имитации . С помощью реализуется квазипараллельная работа компонент. “Квази-” приставка, означающая последовательное обслуживание событий в ИМ, одновременно возникающих в разных компонентах реальной системы.

Корректировка нескольких осуществляется следующим образом. Пусть нескольких при выполнении совпадают (одновременно происходят несколько событий), тогда последовательно обслуживаются с одинаковым (конкретное значение , при котором происходит событие ), при этом не меняется, далее выполняется оператор и вычисляется новое значение . Это значение запоминается и используется для определения момента новой активизации в ИМ .

Активизация означает выполнение следующей активности , с завершением имитации событий меняется . Существует два способа изменения : фиксированных (фиксированный шаг) и переменных (шаг за шагом) интервалов. Рассмотрим на примере реализацию этих способов.

Пусть в системе функционируют 3 компоненты (i=1,2,3), рис. 4.12.


Рис. 4.12. Процесс функционирования компонент и способы изменения модельного времени

Модельное время здесь изменяется по способу фиксированного шага. На величину . События, попадающие в интервал считаются происходящими одновременно. Модельное время изменяется в моменты S₁, S₂, S₃,…,что является событием в ИМ. События обслуживаются управляющей программой модели (УПМ). Обслуживание события сводится к инициации и выполнению соответствующих активностей. Точность появления событий зависит от изменения модельного времени .

В случае способа шагов до следующего события, модельное время изменяется в моменты m₁, m₂, m₃… Сдвиг происходит каждый раз на величину, равную минимальному приращению времени , соответствующую .

Каждое событие в модели является результатом выполнения активности , что требует некоторого ресурса времени ЭВМ. Способ фиксированного шага изменения является более экономичным, т.к. имеет место групповое обслуживание событий. На практике наибольшее распространение получил способ шага до следующего события.