|
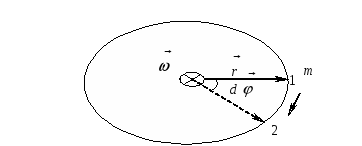
Рис. 2
|
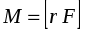
, (3)
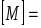
Нм.
Направление вектора момента сил
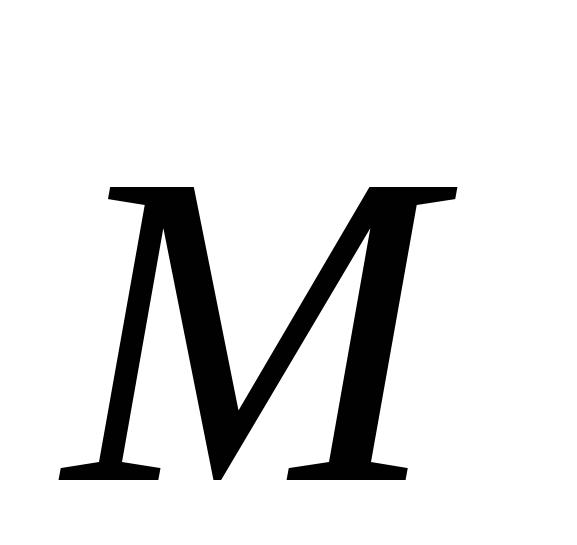
определяется по
правилу векторного произведения (правилу правого винта): вращая винт от первого вектора
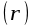
ко второму
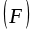
, поступательное движение винта указывает на направление вектора
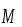
.
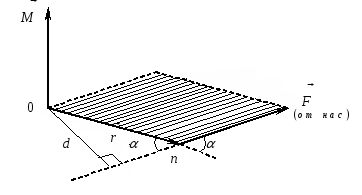
Модуль вектора
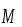
определяется как
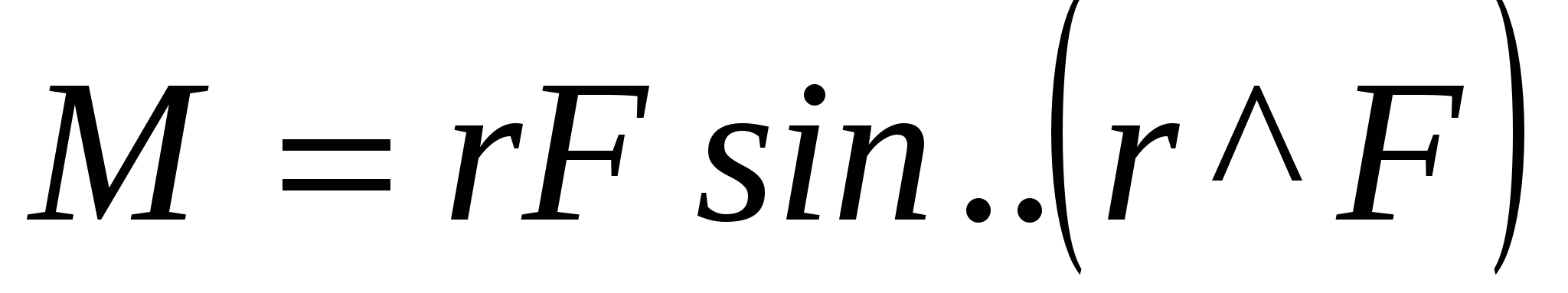 (4)
(4)и численно равен площади заштрихованной фигуры (рис. 2). Учитывая, что
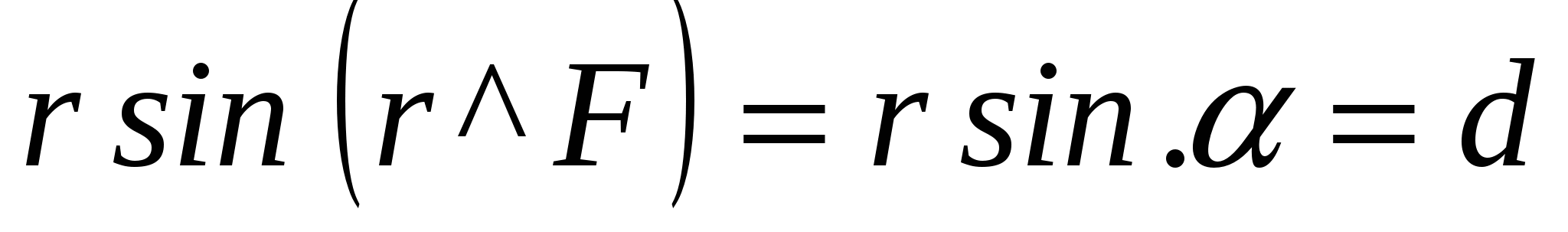
, можно записать
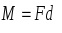
,
(5)где
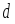
- плечо силы, т.е. кратчайшее расстояние от точки
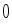
, относительно которой происходит вращение, до линии действия силы
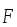
.
|
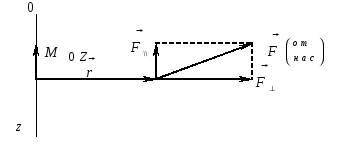
Рис. 3
|
При рассмотрении момента сил относительно оси
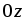
необходимо спроектировать векторное произведение
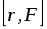
на эту ось, т.е.
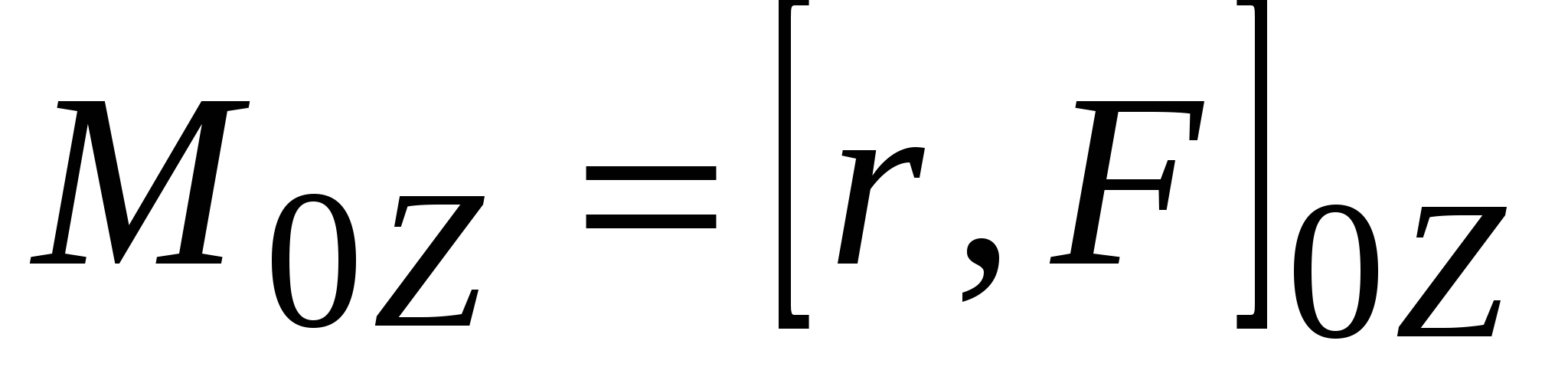
. (6)
Из рис. 3 видно, что момент силы создается лишь силой
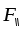
(силой, параллельной оси
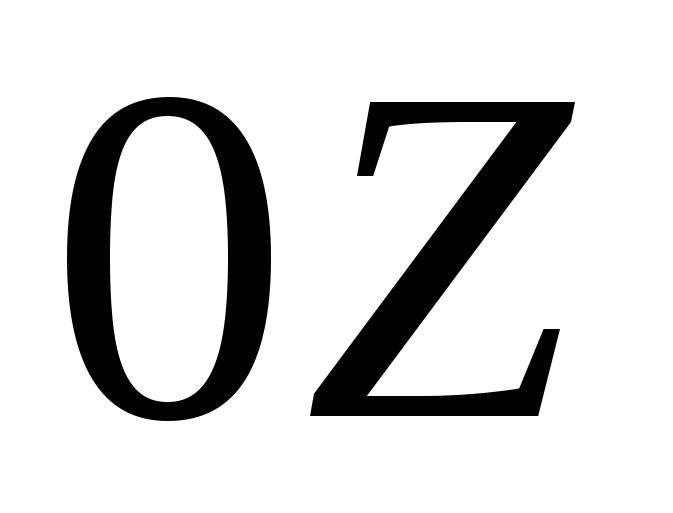
), момент силы
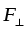
равен нулю.
Для нахождения связи между угловым ускорением
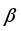
и моментом сил
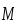
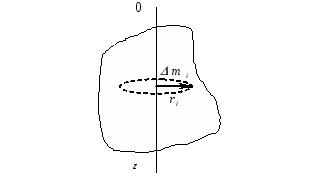
, действующих на него, рассмотрим движение одной какой-то частицы вращающегося тела (рис.4).
|
Рис. 4
|
Пусть частица с массой
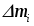
находится на расстоянии
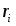
от оси вращения
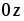
. На
частицу могут действовать как внутренние, так и внешние силы. Внешние силы приложены со стороны других тел, а внутренние – со стороны частей того же самого тела.
Обозначим проекцию суммы внутренних сил, действующих на
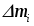
, на направление, перпендикулярное к
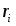
, как
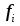
, а проекцию суммы внешних сил как
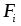
. Тогда, применяя 2-ой закон Ньютона к каждой точке вращающегося тела, можно записать:
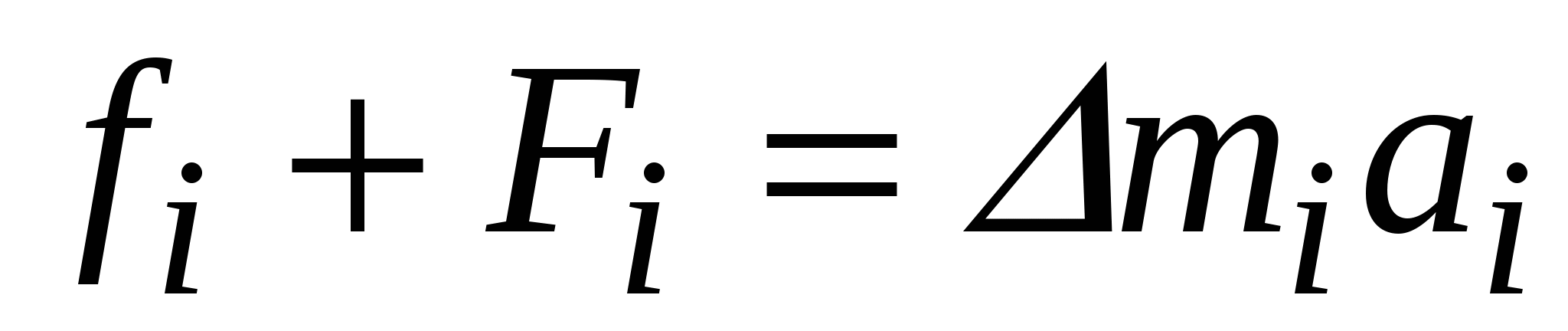

, (7)
где
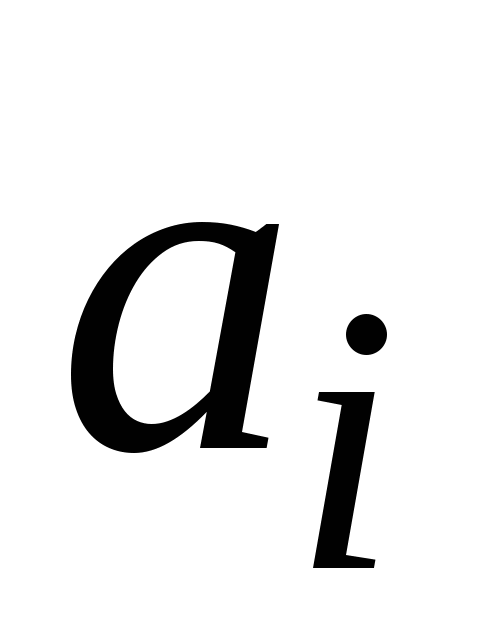
– линейное ускорение точки.
Если умножить выражение (7) на
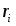
и учесть, что
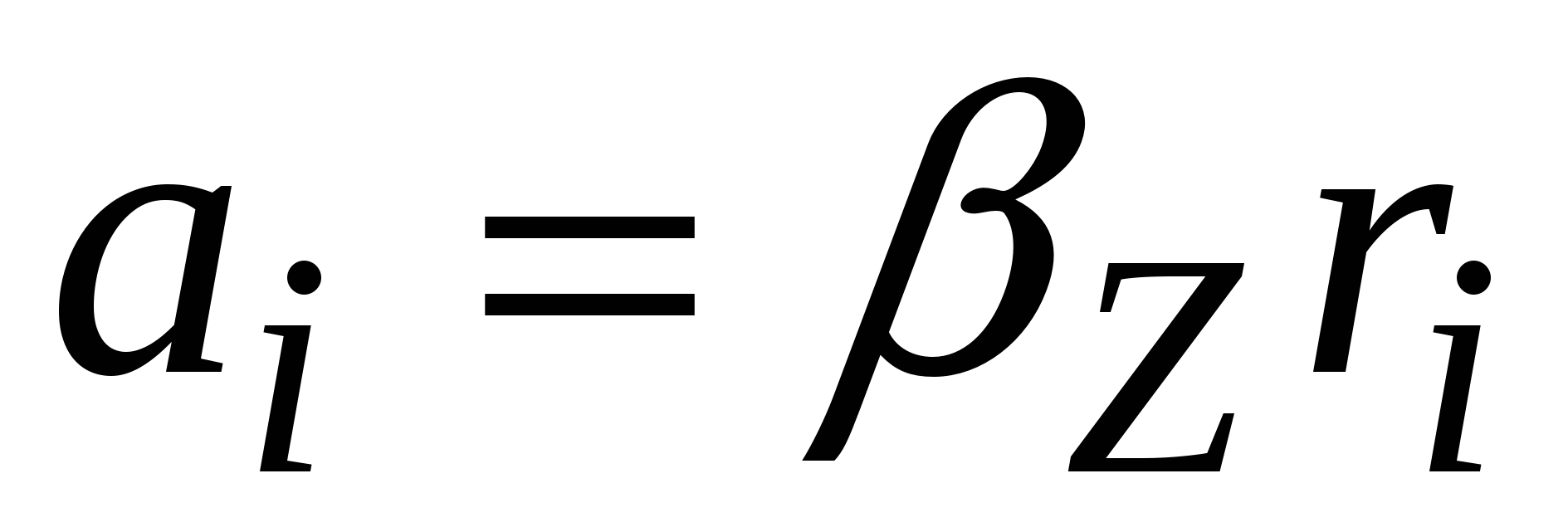
, то получим:
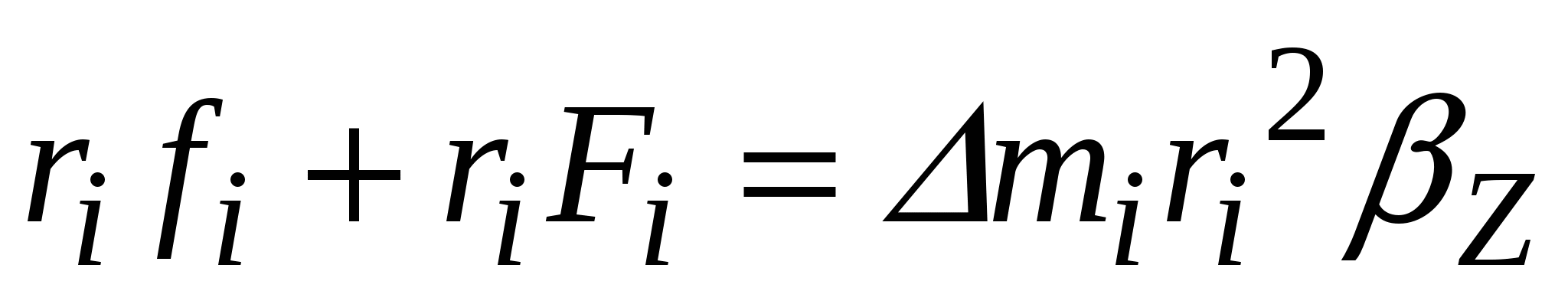
, (8)
где
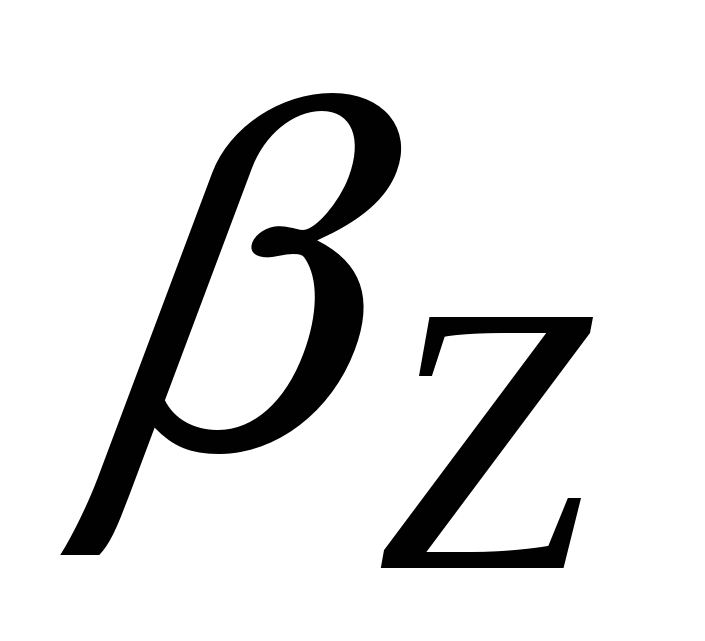
- проекция углового ускорения на ось OZ.
Величина
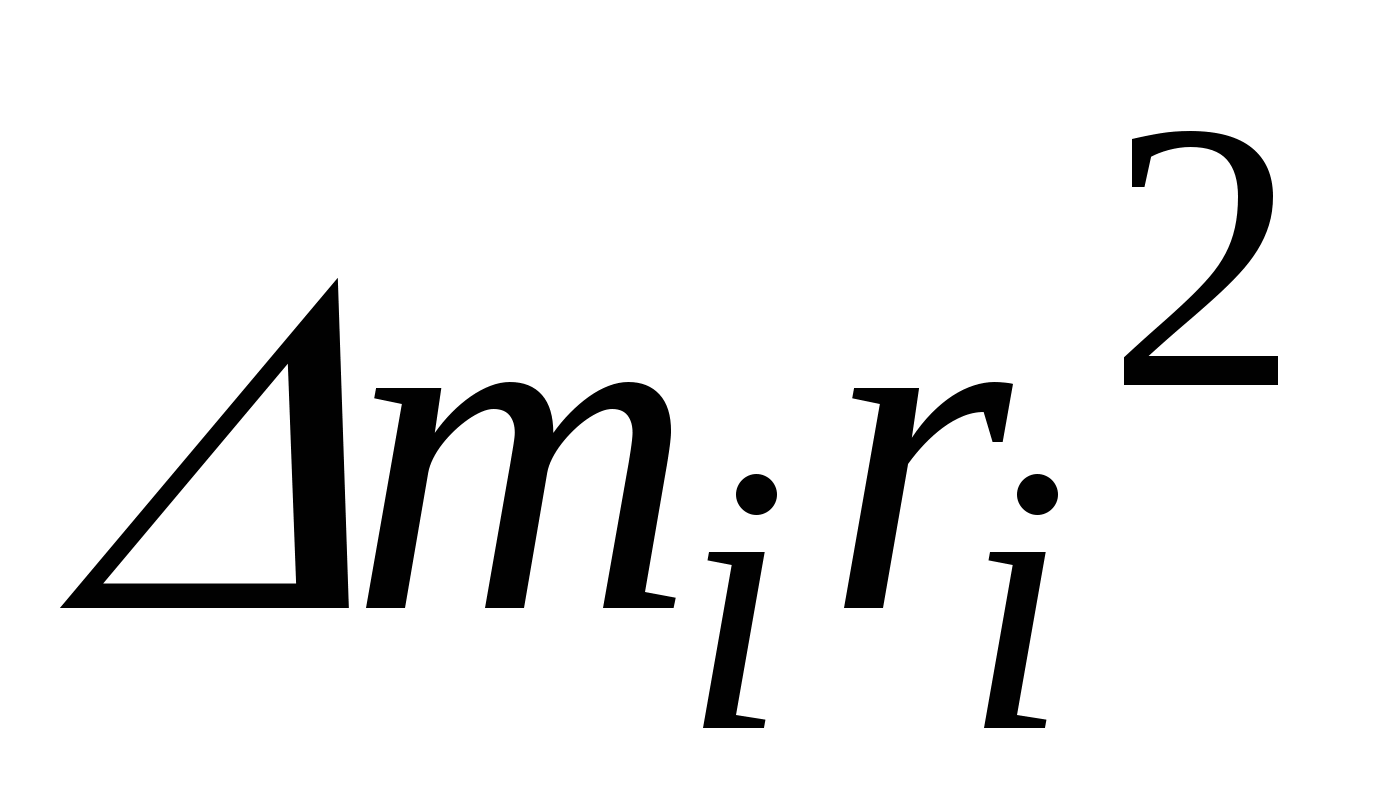
,численно равная произведению массы на квадрат расстояния от оси вращения, называется
моментом инерции точки относительно оси вращения.
Величины
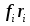
и
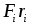
определяют моменты внутренних и внешних сил, действующих на
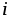
-ю точку.
Уравнения типа (7) и (8) можно записать и для остальных точек тела. Суммируя выражение (8) по всем элементам тела, получим:
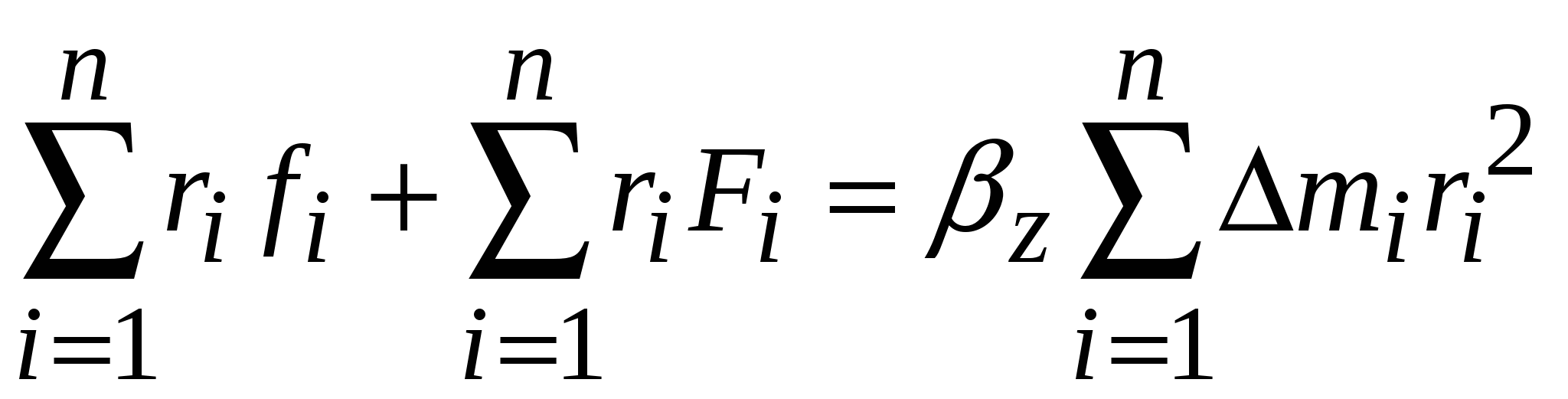
, (9)
где
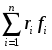
- сумма проекций на ось
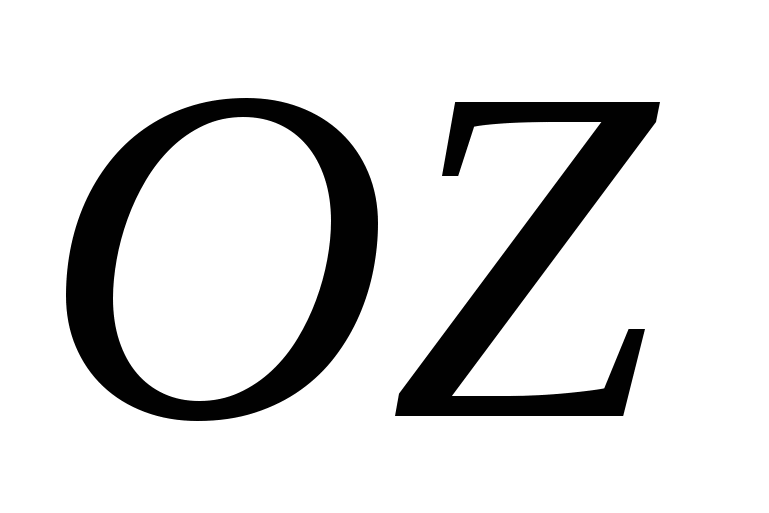
всех внутренних моментов сил (
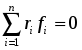
, т.к. каждая внутренняя сила имеет равную и противоположную себе силу, приложенную к другой частице тела с тем же самым плечом);
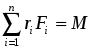
- сумма проекций на ось
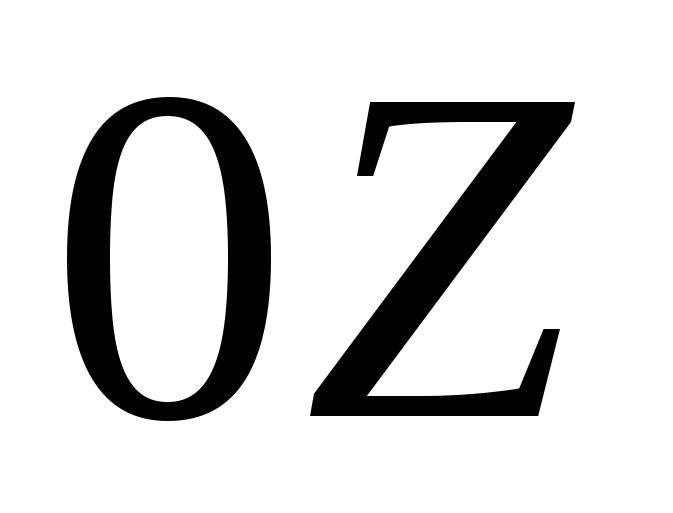
всех внешних моментов сил, приложенных к телу;
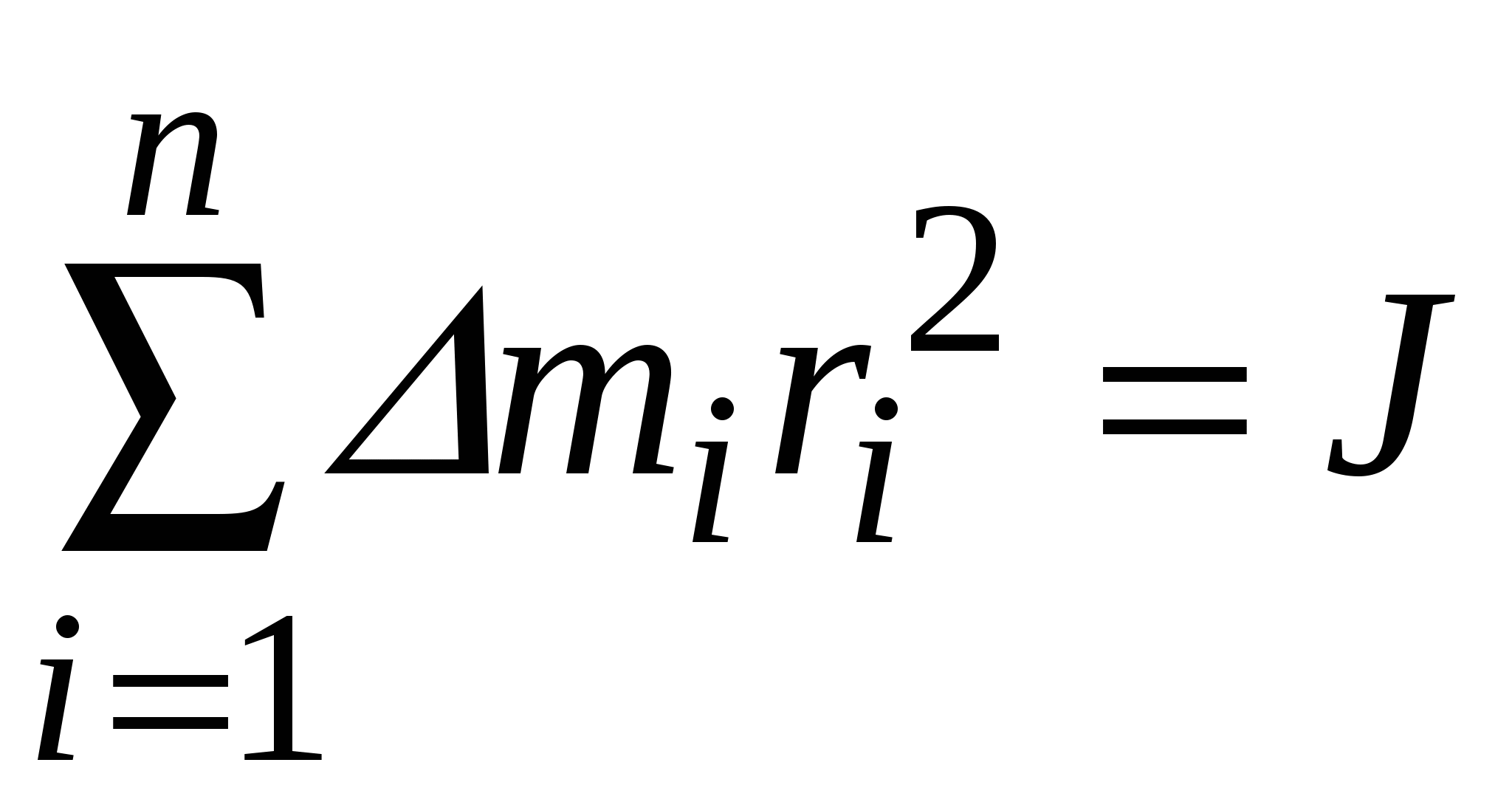
- момент инерции твердого тела относительно оси вращения
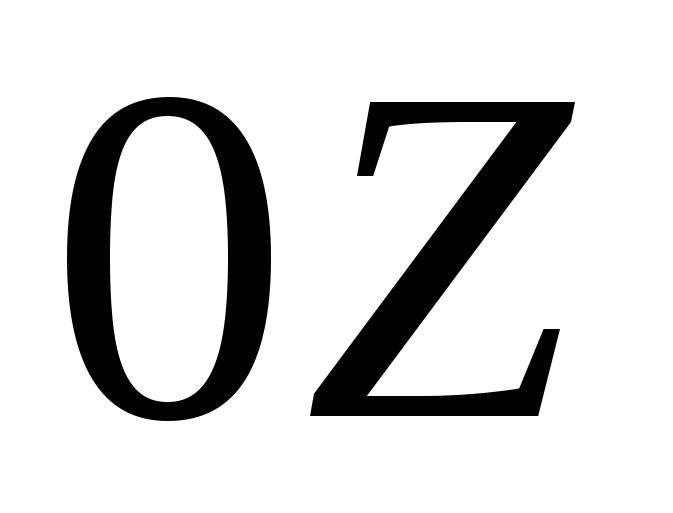
, равный сумме моментов инерции отдельных элементов тела (
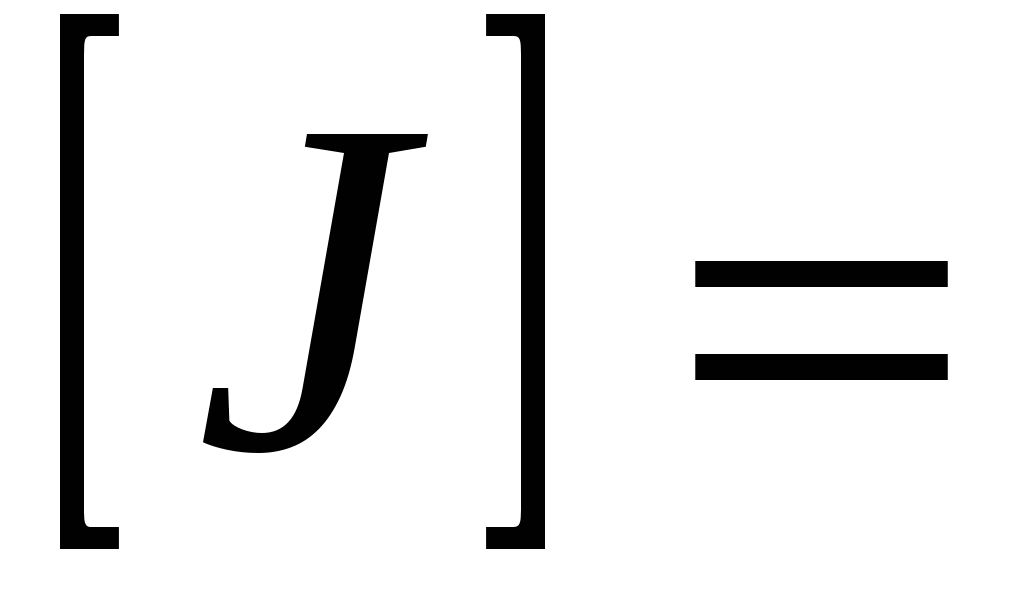
кгм
2).
Использовав все обозначения, получим:
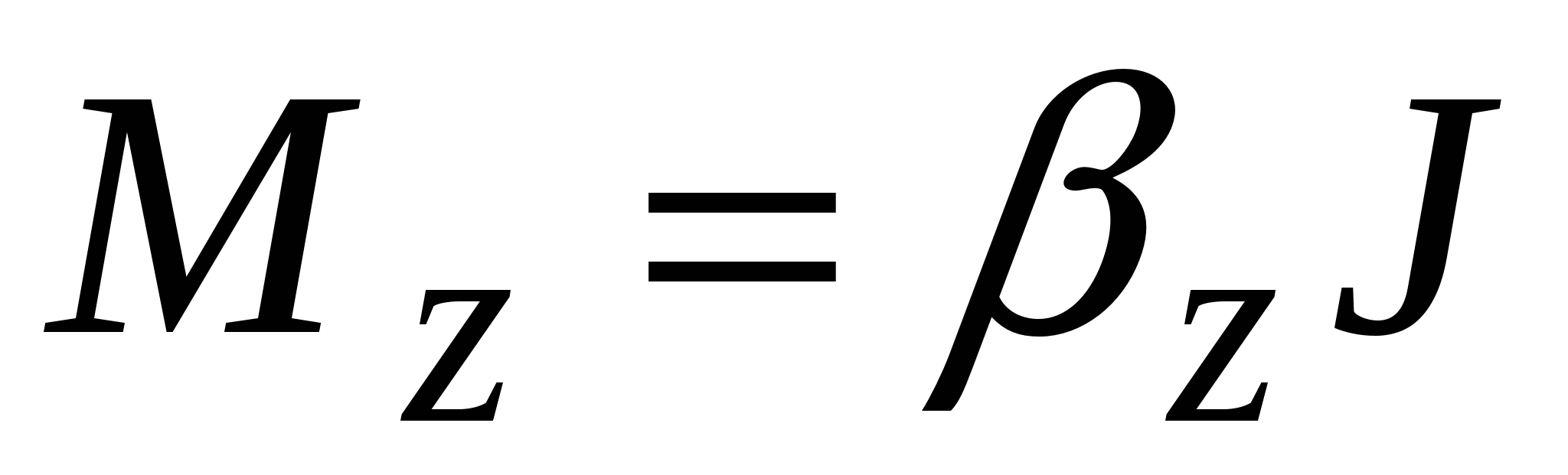
, (10)
откуда
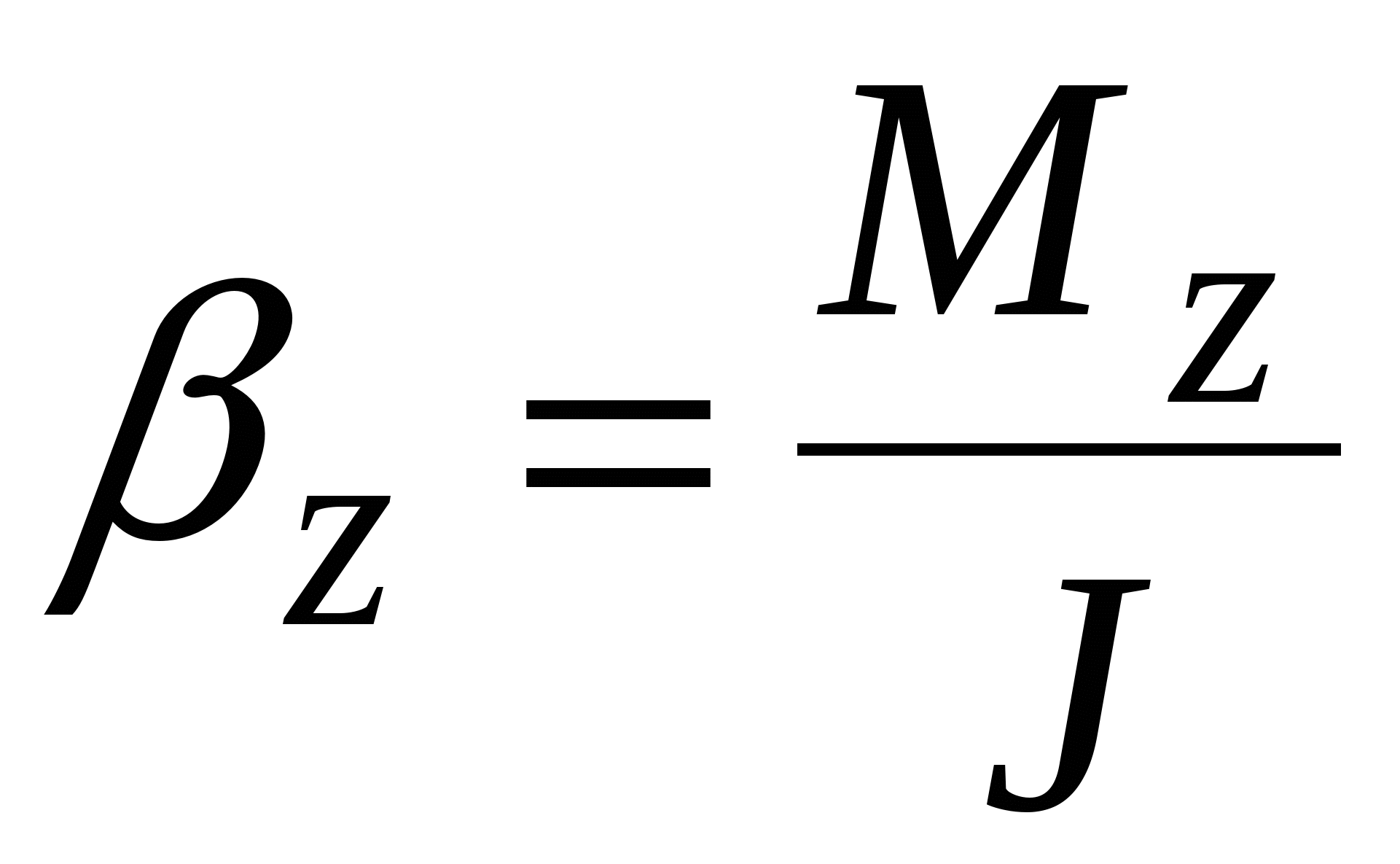
(11)
основной закон динамики вращательного движения.
В векторном виде этот закон может быть записан:
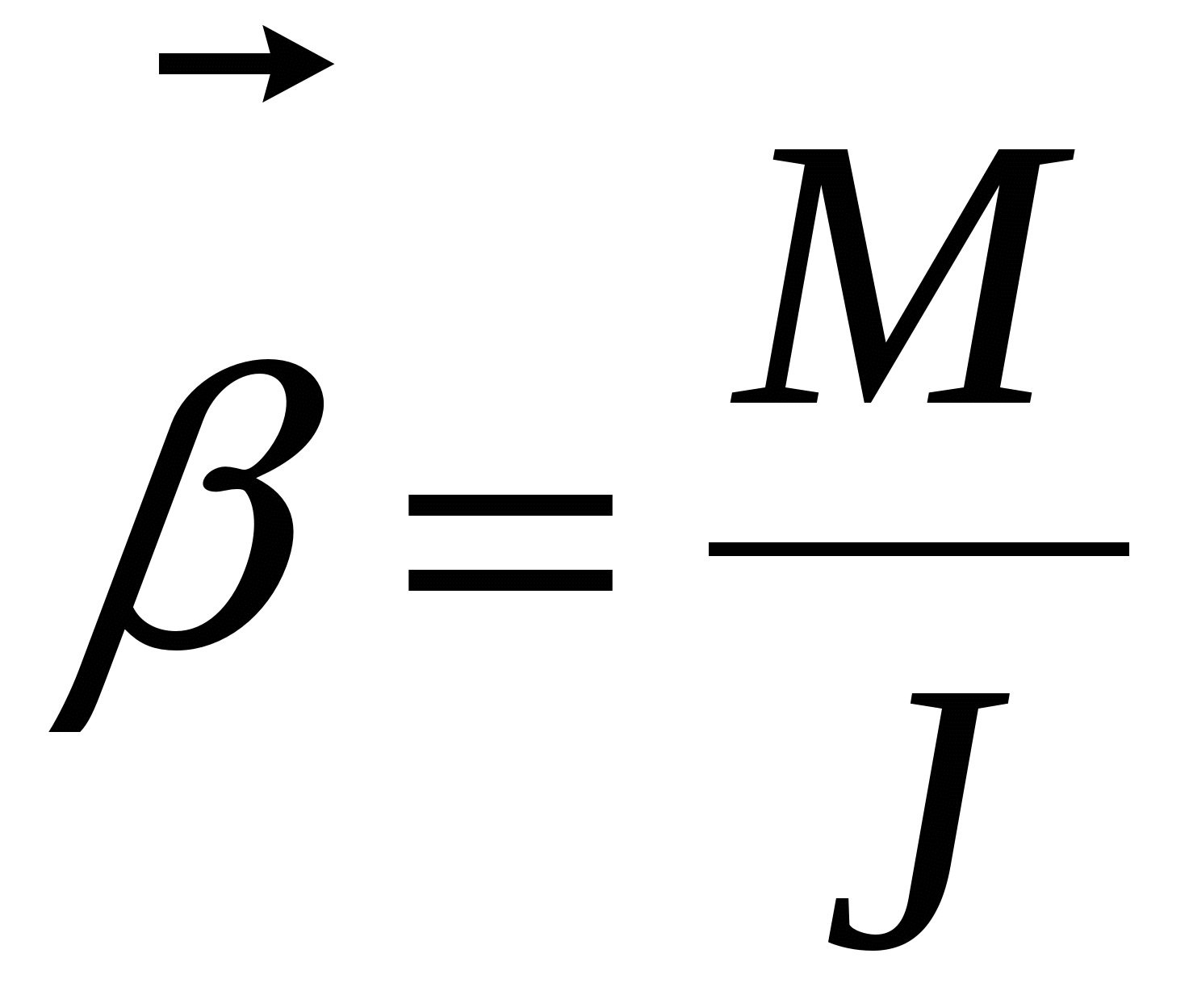
.
(12)то есть
угловое ускорение пропорционально действующему внешнему моменту сил и обратно пропорционально моменту инерции твердого тела относительно оси вращения.Этот закон аналогичен закону динамики для поступательного движения:
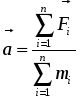
,
(13)где
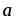
- линейное ускорение;
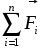
-
сумма всех внешних сил;
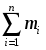
- сумма всех элементарных масс.
Используя аналогию, можно сделать вывод о том, что момент инерции

при вращательном движении играет такую же роль, как и масса
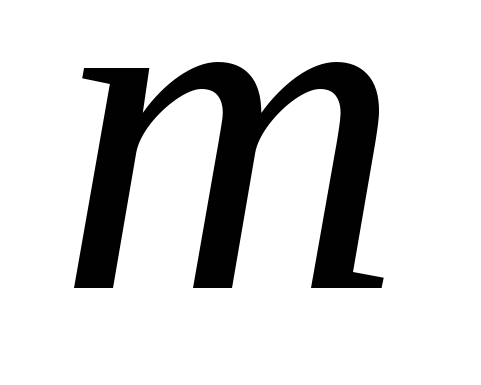
при поступательном движении, т.е. момент инерции является мерой инертности тела при вращательном движении.
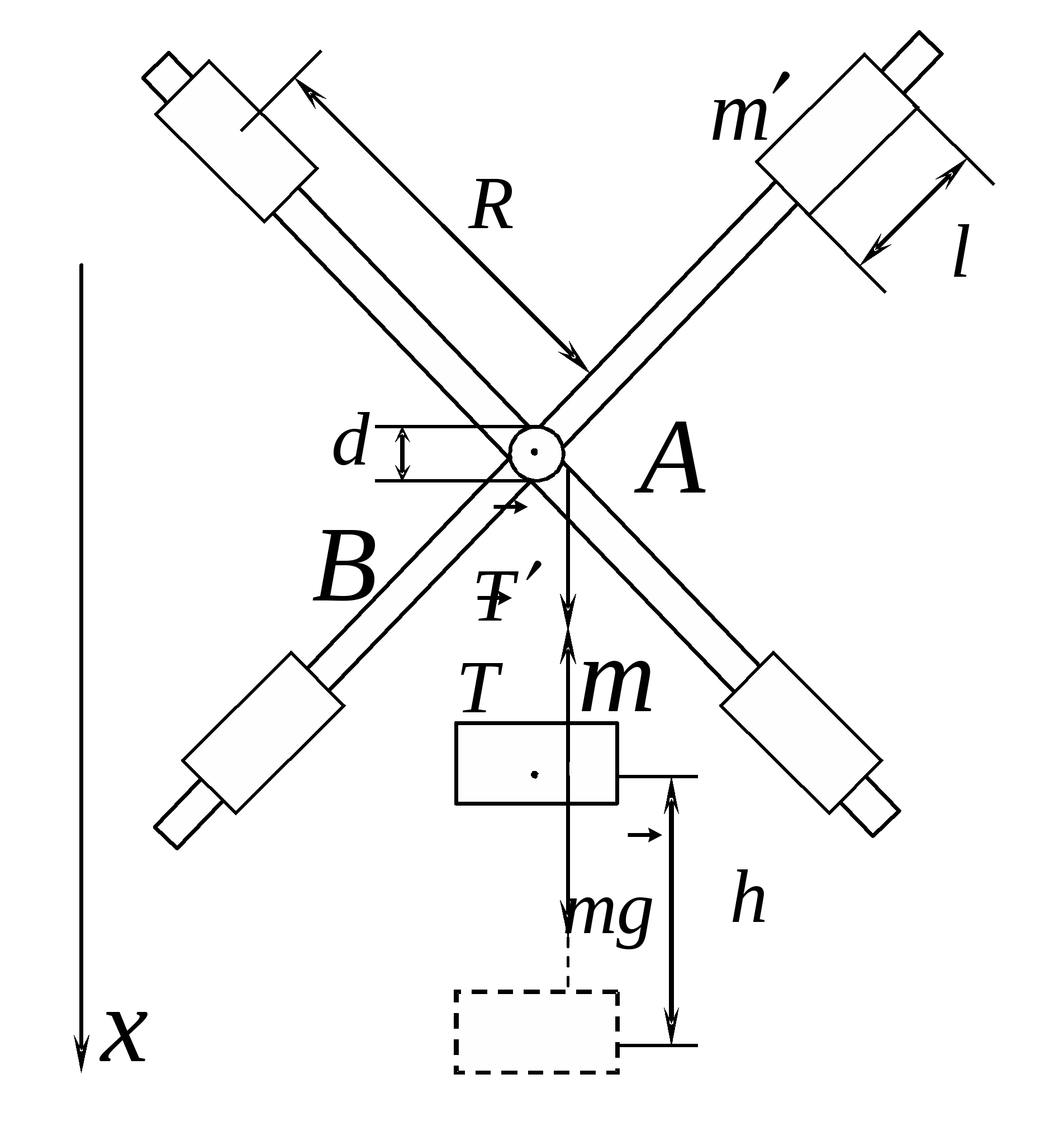
Проверка основного закона вращательного движения производится на приборе, называемом маятником Обербека (рис. 5).
МЕТОДИКА ЭКСПЕРИМЕНТА И ОПИСАНИЕ УСТАНОВКИ
Маятник Обербека состоит из вала
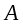
диаметром
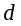
, к которому прикреплены 4 одинаковых стержня
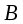
, расположенных под углом 90
0 друг к другу (рис. 5). На каждом стержне закрепляется по одному грузу одинаковой массы
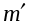
. Благодаря возможности фиксировать данные грузы на различных расстояниях от оси вращения это позволяет изменять момент инерции маятника Обербека. На вал
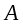
наматывается нить, к концу которой прикрепляется груз массой
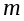
(значение
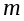
можно менять). Под действием груза нить, разматываясь с вала А, приводит всю систему во вращательное движение.
|
Рис. 5
|
В применении к маятнику Обербека экспериментально определим основные величины, входящие в уравнение (11).
Угловое ускорение. Пусть
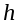
- высота падения груза массой
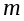
, прикрепленного к концу нити,
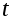
- время падения груза. Тогда линейное ускорение груза определяется из уравнения кинематики
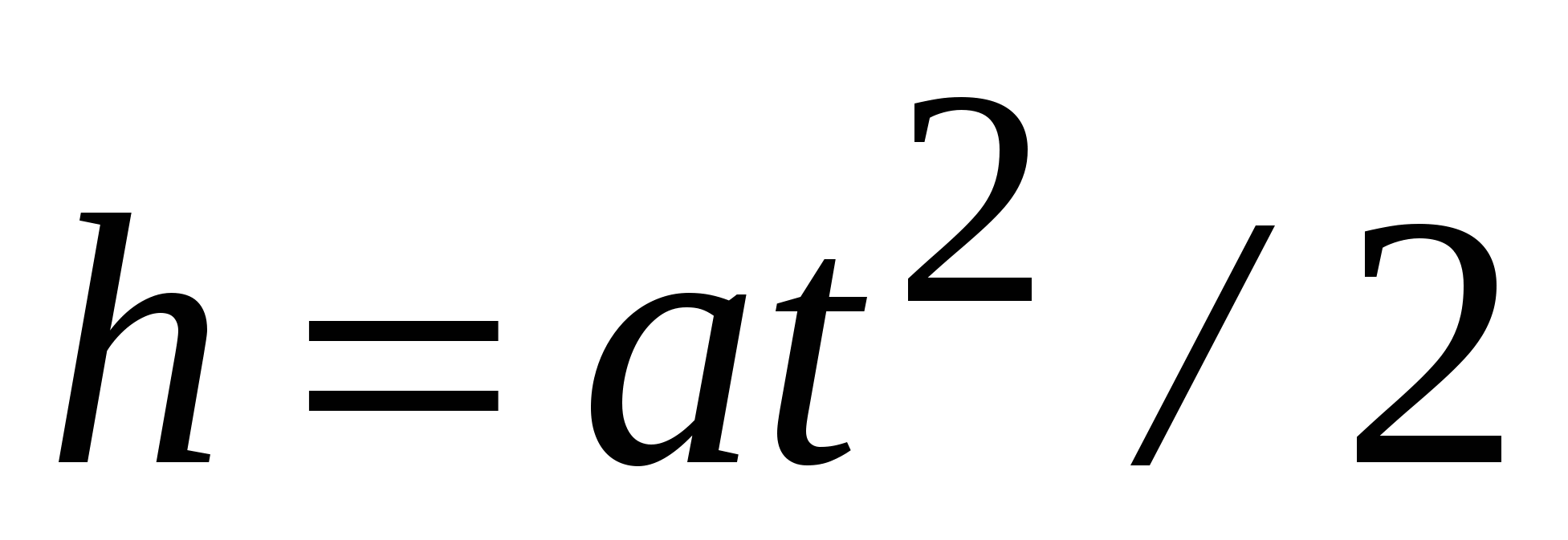
, как
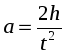
. (14)
С таким же линейным ускорением движутся точки вала
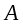
, находящиеся на расстоянии
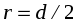
от оси вращения. Используя связь между линейным и угловым ускорениями
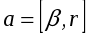
(15)
и учитывая, что
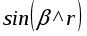
=1, получим
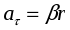
;
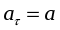
. (16)
Следовательно,
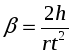
. (17)
Момент сил. Вращающий момент системы создается силой упругости нити (силой натяжения нити
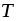
).
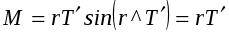
.
Учитывая, что
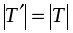
и
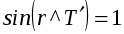
, имеем
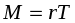
, (18)
где
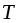
-
сила натяжения нити;
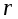
- радиус действия силы, совпадающий с радиусом валика
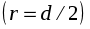
.
Натяжение нити можно определить так. Запишем 2-ой закон Ньютона для падающего груза:
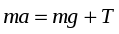
. (19)
Учитывая выбранное направление
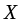
(рис. 5), выражение (19) можно записать в виде:
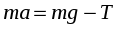
,
откуда
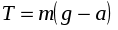
,
а момент сил равен
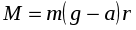
. (20)
Момент инерции. Так как момент инерции – величина аддитивная, то полный момент инерции системы равен:
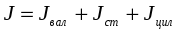
. (21)
Если составляющие маятник части являются геометрически правильными и простыми по своей форме, то все три составляющие можно рассчитать теоретически. В настоящей конструкции прибора такой расчет для
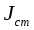
(стержня) и
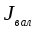
(валика) несколько затруднен. Поэтому теоретически рассчитывается только
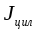
(цилиндра). По теореме Штейнера для
четырех цилиндров момент инерции равен:
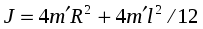
, (22)
где
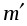
- масса одного цилиндра;
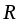
- расстояние от оси вращения до центра масс цилиндра;
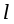
- длина цилиндра (рис. 5).
Момент инерции системы будет равен
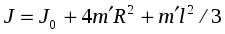
. (23)
Значение
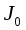
можно определить опытным путем. Для этого со стержней маятника снимаются 4 цилиндра и система приводится во вращательное движение под действием груза массой
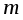
. Момент инерции
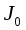
равен

. (24)
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
ЗАДАНИЕ 1. Определить момент инерции
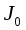
.
Снять со стержней маятника цилиндрические грузы.
Измерить диаметр 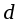 вала штангенциркулем и определить
вала штангенциркулем и определить 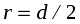 .
.
Определить массу 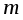 груза, подвешенного к нити, которая наматывается на вал.
груза, подвешенного к нити, которая наматывается на вал.
Предоставить возможность грузу падать и зафиксировать время 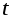 падения груза с высоты
падения груза с высоты 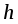 (
(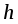 измеряется с помощью вертикального масштаба).
измеряется с помощью вертикального масштаба).
Измерения
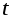
нужно выполнить несколько раз (не менее трех), оставляя высоту падения постоянной. Данные занести в таблицу 1.
По формулам 14, 17, 20, 24 рассчитать линейное ускорение 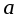 , угловое ускорение
, угловое ускорение 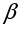 , момент сил
, момент сил 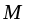 , момент инерции
, момент инерции 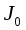 и результаты занести в табл. 1 для двух различных падающих масс
и результаты занести в табл. 1 для двух различных падающих масс 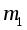 и
и 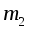 .
.
Таблица 1
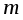 , кг , кг
|
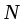
|
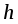 , м , м
|
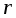 , м , м
|
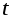 , с , с
|
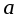 , ,
м/с2
|
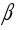 , ,
рад/с2
|
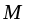 , ,
Нм
|
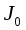 , ,
кгм2
|
∆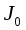 , кгм2 , кгм2
|
σ, кгм2
|
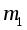
|
1
2
3
|
|
|
|
|
|
|
|
|
|
средние значения
|
|
|
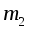
|
1
2
3
|
|
|
|
|
|
|
среднее значение
|
|
|
|
|
Изменяя массу подвешенного к нити груза, можно изменить силу натяжения нити, а, следовательно, и момент сил. Однако момент инерции маятника не должен зависеть от изменения этих внешних воздействий, и с учетом погрешностей момент инерции должен принимать одинаковые значения. Это дает возможность найти среднее значение
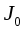
.
Оценить погрешность измерений
Записать конечный результат в виде J0=J0ср±2σ.
ЗАДАНИЕ 2. Проверка основного закона динамики вращательного движения. Проверка соотношения
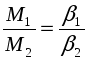 (26)
(26)при
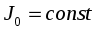
.
Для проверки этого соотношения можно воспользоваться данными из табл. 1. Найдем отношения
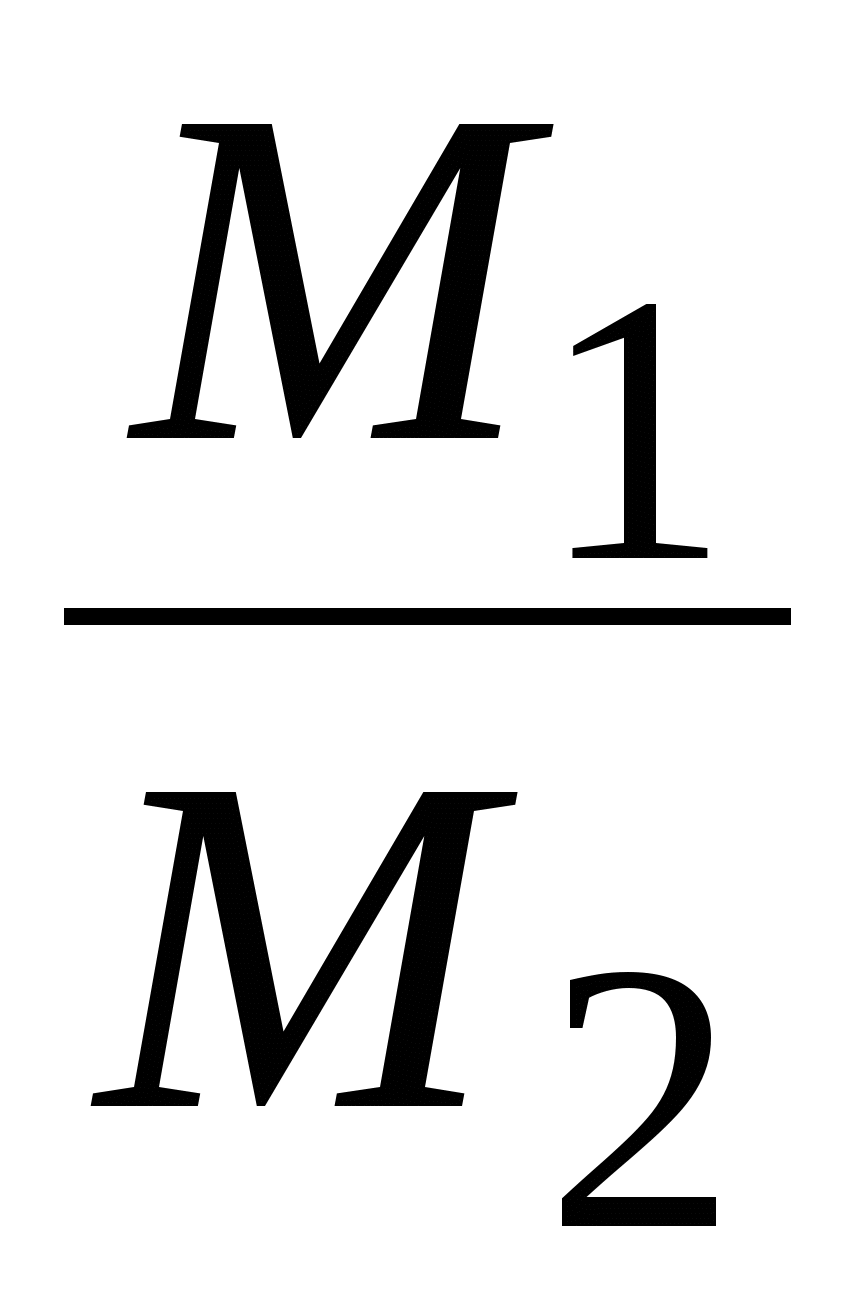
,
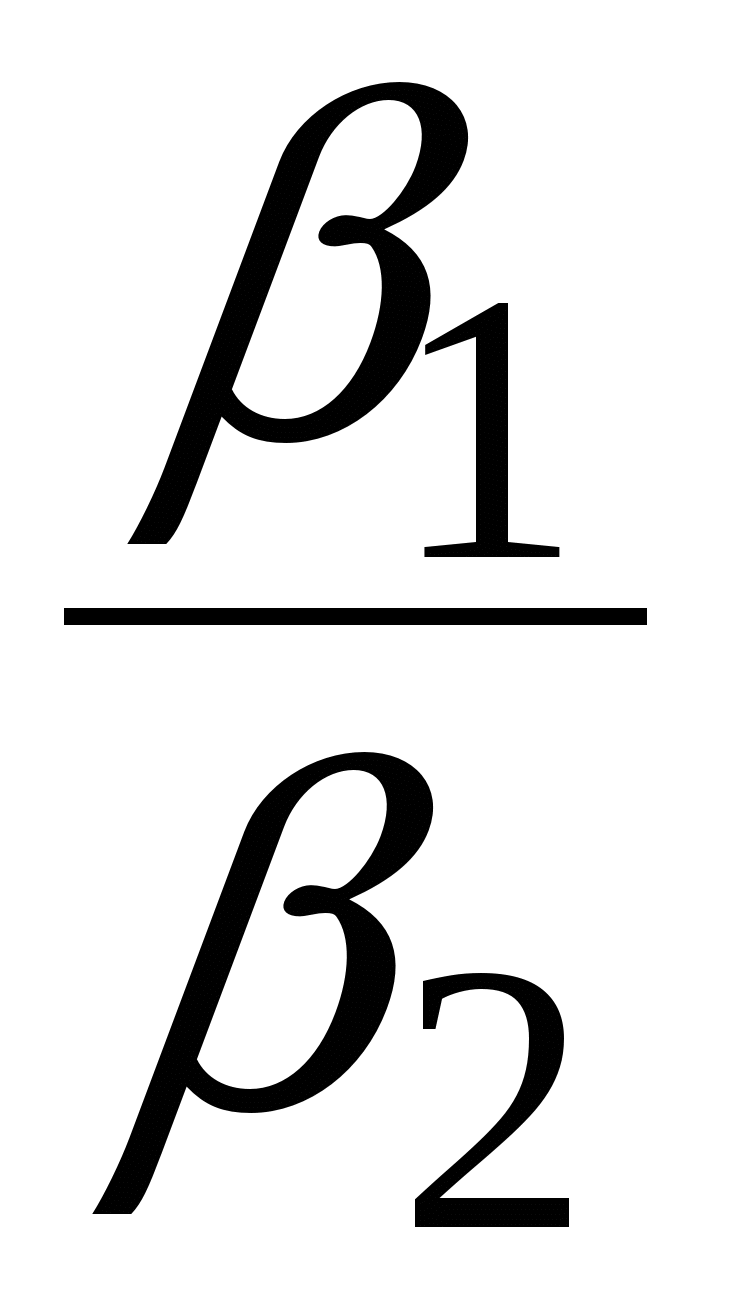
и сравним их между собой. Должно выполняться равенство (26).
ЗАДАНИЕ 3. Изучение зависимости момента инерции крестообразного маятника от положения грузов на стержнях, т.е. от распределения его массы по отношению к оси вращения. Проверка соотношения
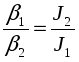 (27)
(27)при
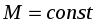
.
Надеть на стержни цилиндрические грузы и расположить их на определенном расстоянии 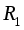 от оси вращения. После закрепления грузов необходимо убедиться в том, что маятник достаточно сбалансирован, т.е. привести его в состояние безразличного равновесия путем перемещая грузов на стержнях на небольшие расстояния.
от оси вращения. После закрепления грузов необходимо убедиться в том, что маятник достаточно сбалансирован, т.е. привести его в состояние безразличного равновесия путем перемещая грузов на стержнях на небольшие расстояния.
Подвесить груз массой 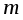 1 и провести все измерения, необходимые для определения момента инерции маятника (см. табл. 1).
1 и провести все измерения, необходимые для определения момента инерции маятника (см. табл. 1).
Рассчитать по формуле (17) угловое ускорение 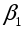 и по формуле (24) момент инерции
и по формуле (24) момент инерции 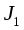 маятника с цилиндрами массой
маятника с цилиндрами массой 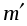 (все измерения производить в соответствии с заданием 1, но только лишь с одной падающей массой
(все измерения производить в соответствии с заданием 1, но только лишь с одной падающей массой 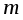 ).
).
Измерив 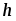 и
и 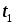 (время падения груза массой
(время падения груза массой 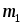 ), рассчитать по формуле (17) угловое ускорение
), рассчитать по формуле (17) угловое ускорение 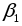 .
.
Расположив цилиндрические грузы на другом расстоянии
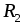
от оси вращения
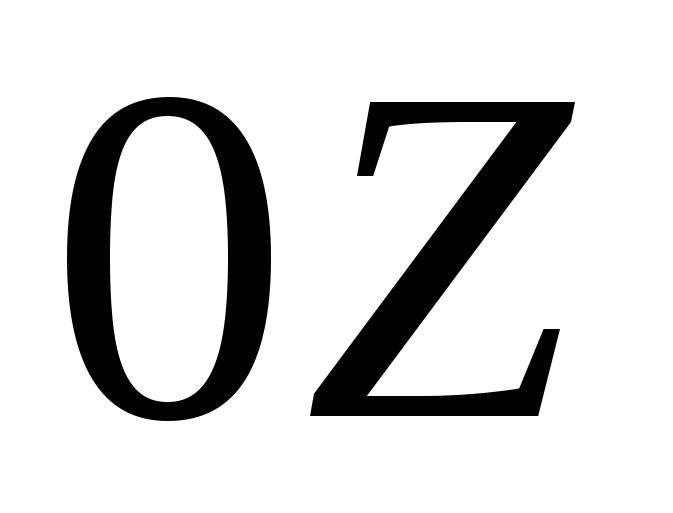
, провести аналогичные измерения.
По формуле (17) рассчитать угловое ускорение 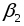 (если
(если 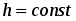 , то необходимо только зафиксировать время
, то необходимо только зафиксировать время 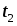 падения груза массой
падения груза массой 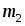 ).
).
Полученные данные занести в таблицу 2.
Таблица 2
При 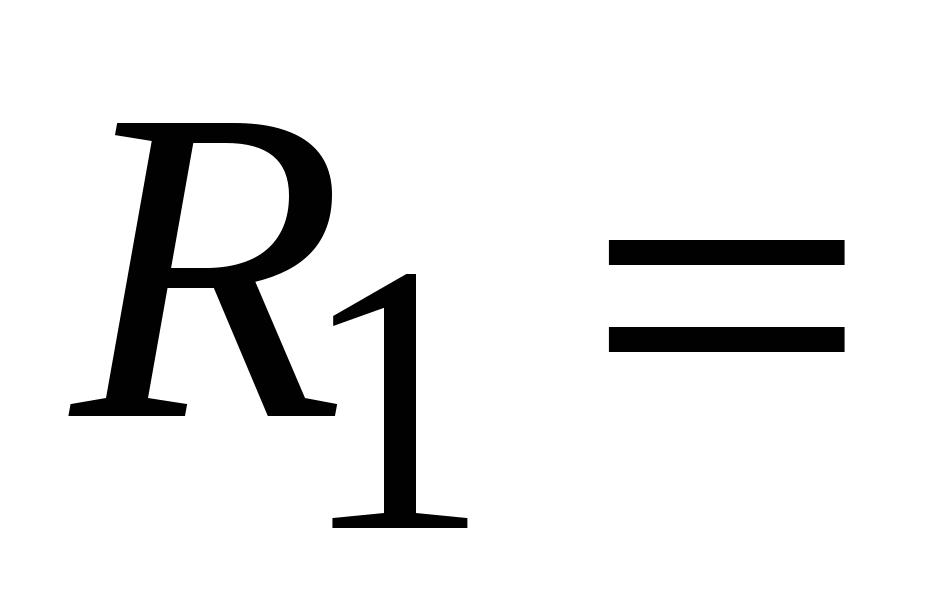
|
|
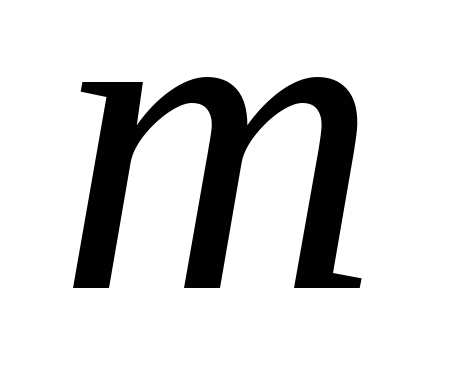 , кг , кг
|
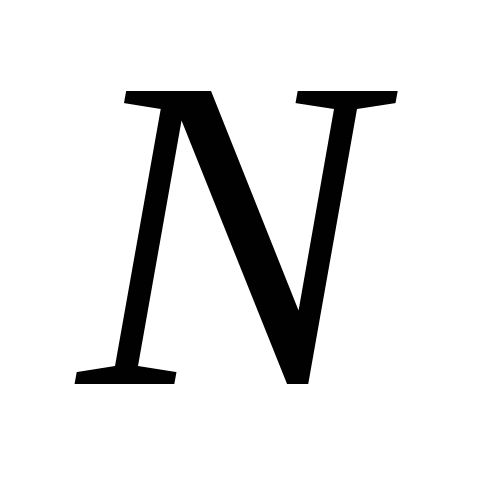
|
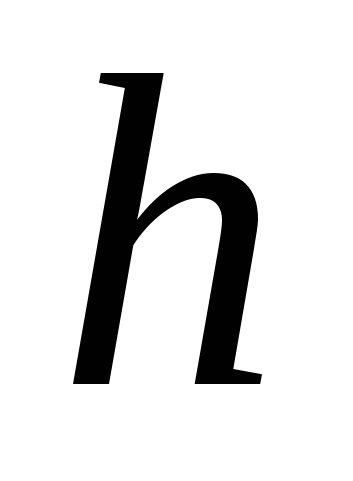 , м , м
|
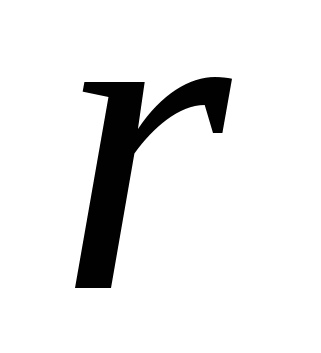 , м , м
|
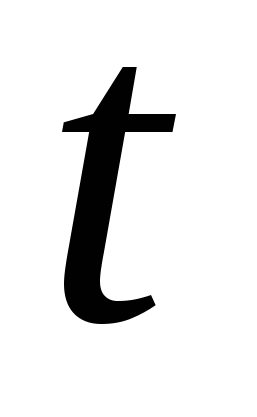 , с , с
|
 , ,
м/с2
|
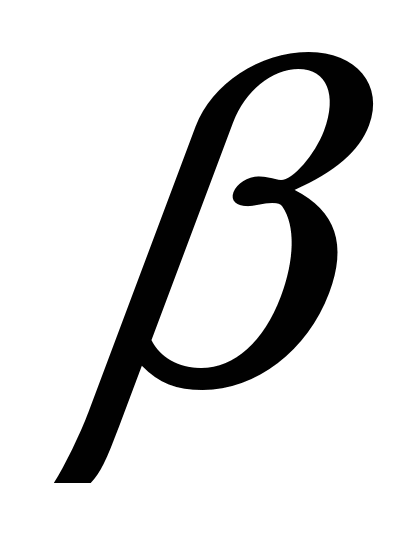 , ,
рад/с2
|
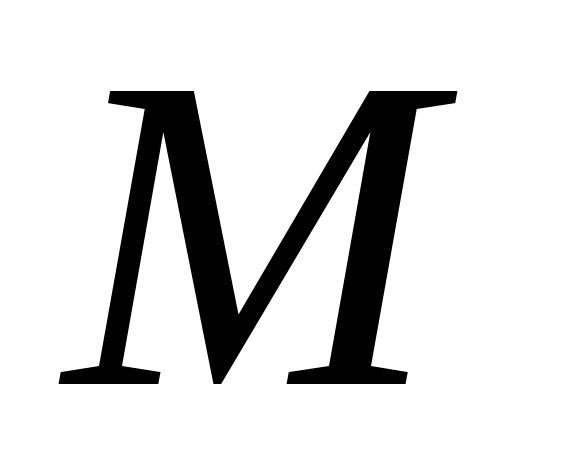 , ,
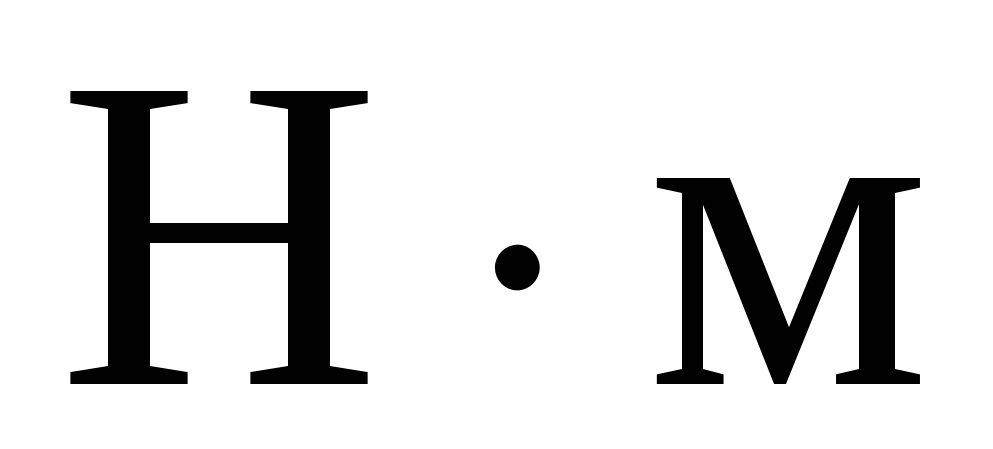
|
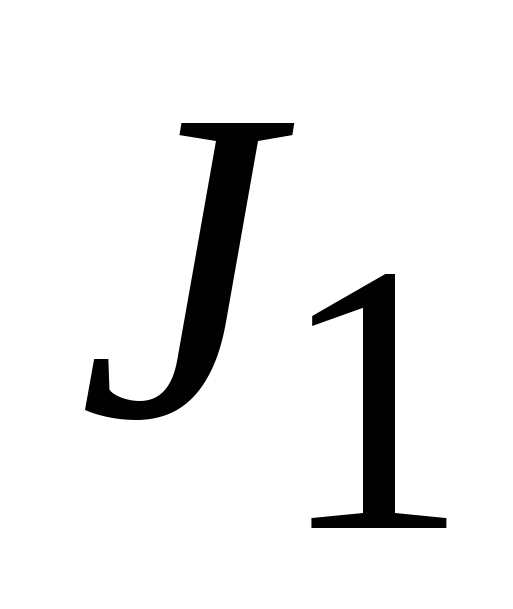 , ,
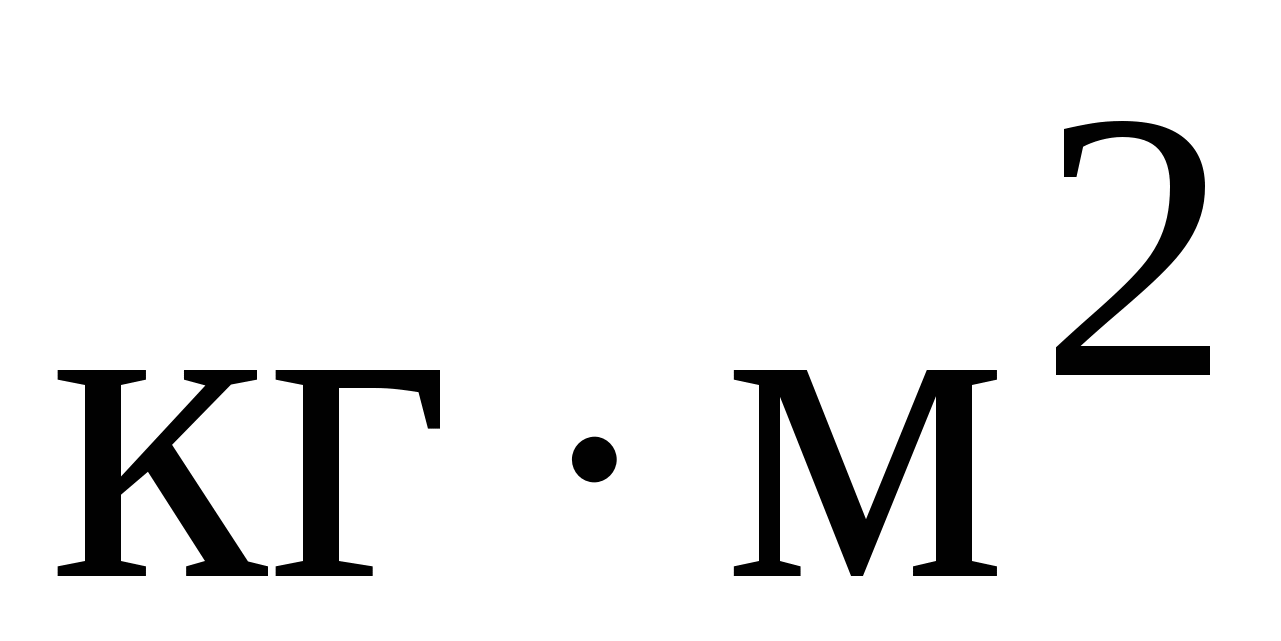
|
∆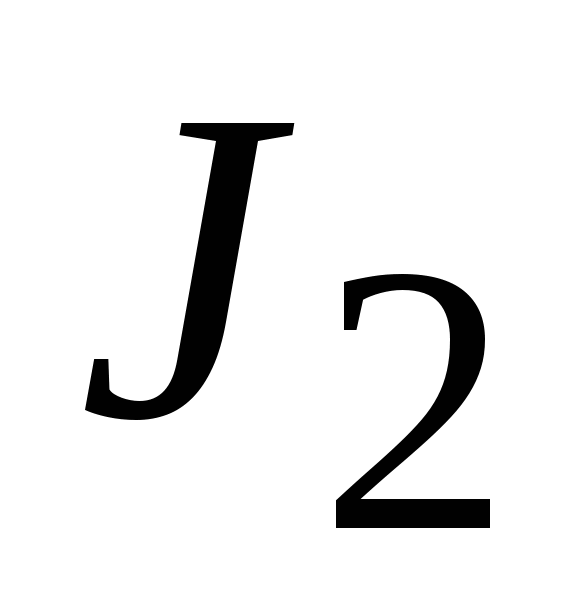 , ,
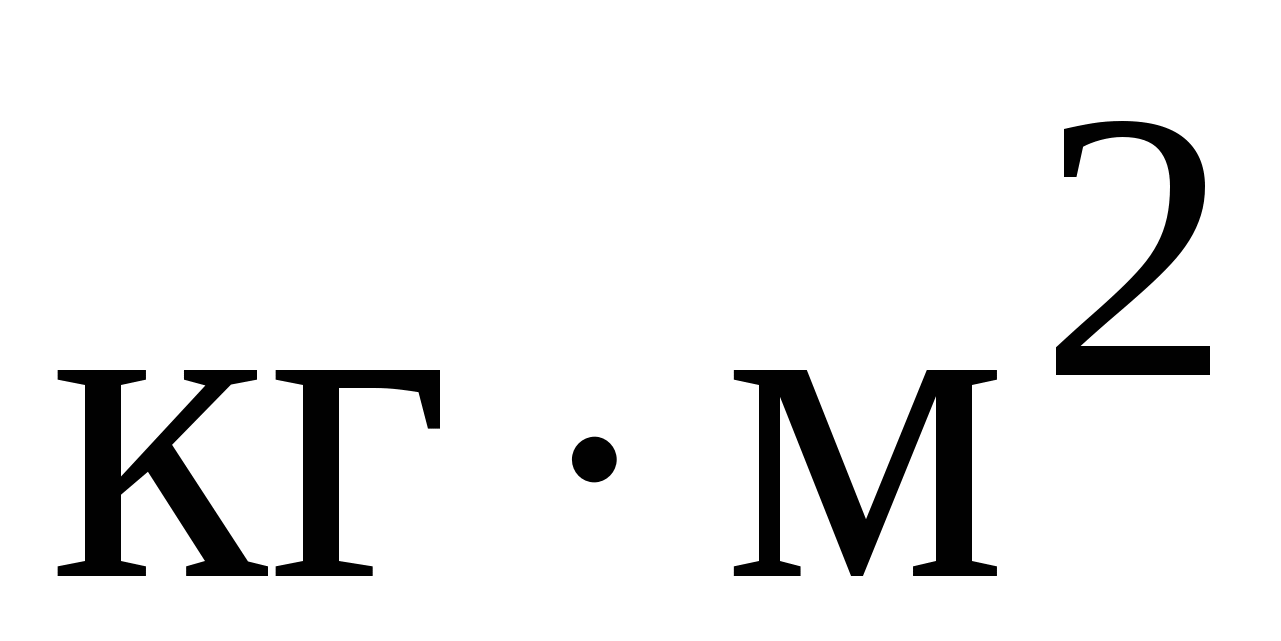
|
σ,
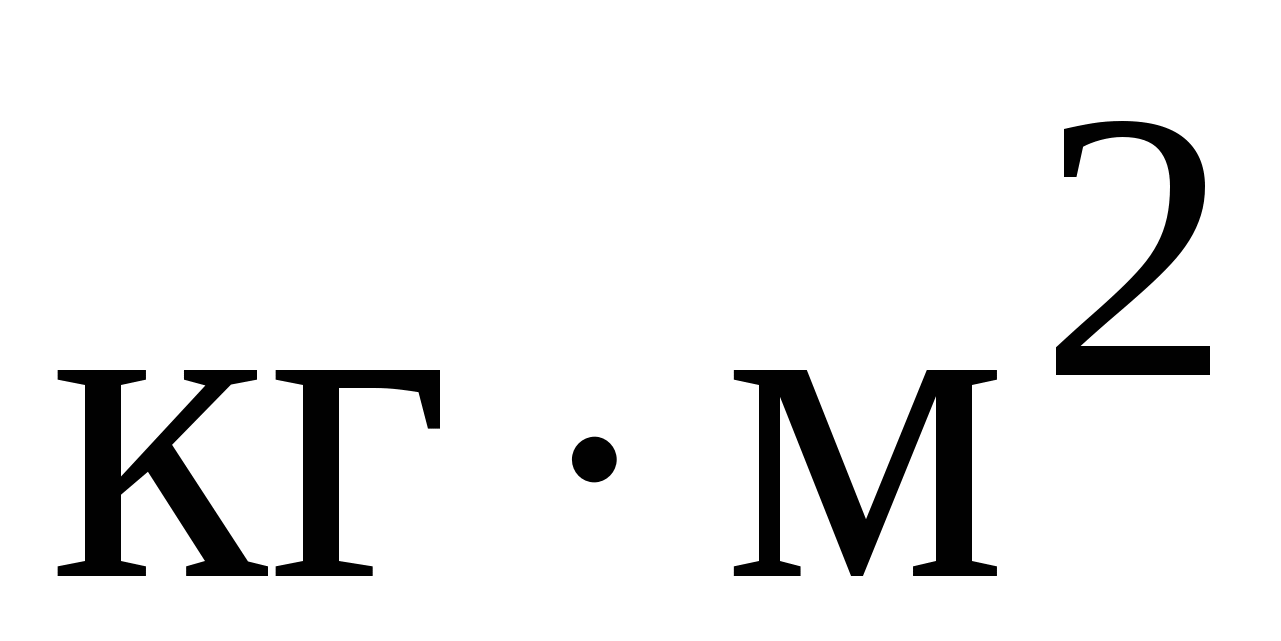
|
|
1
2
3
|
|
|
|
|
|
|
|
|
|
Средние значения
|
|
|
|
|
При 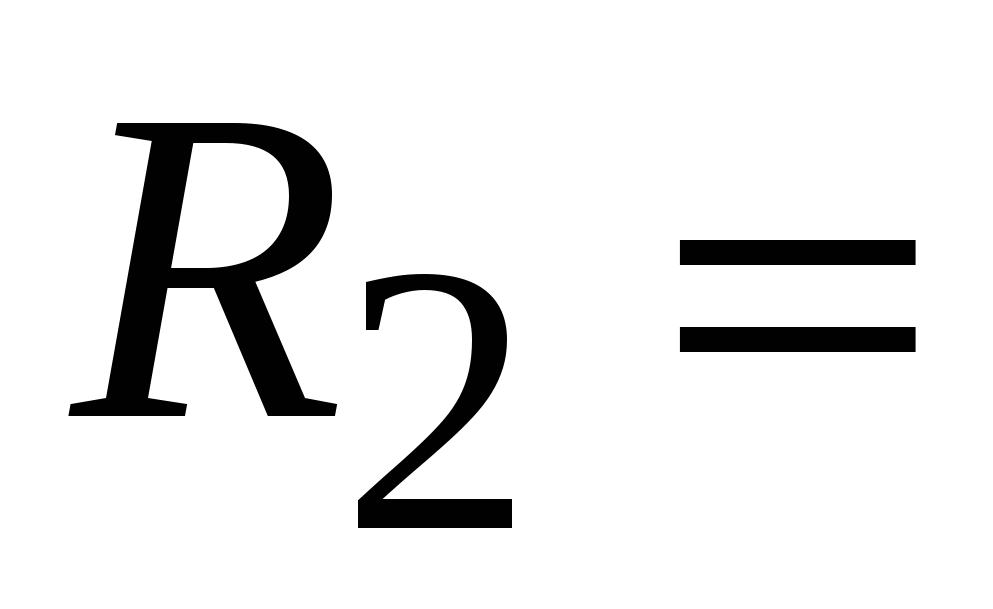
|
|
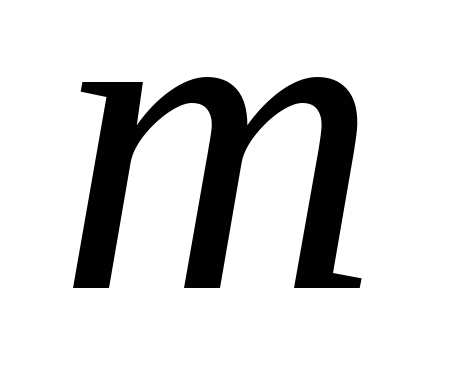 , кг , кг
|
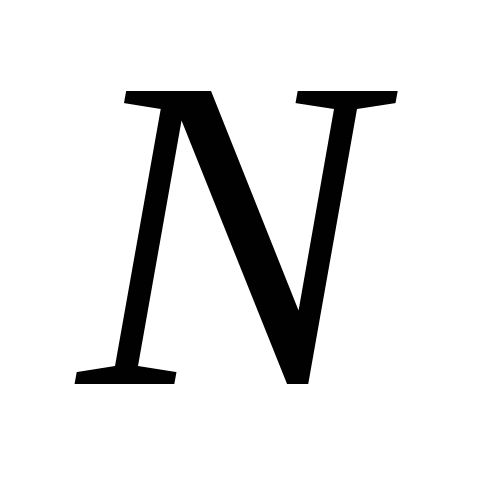
|
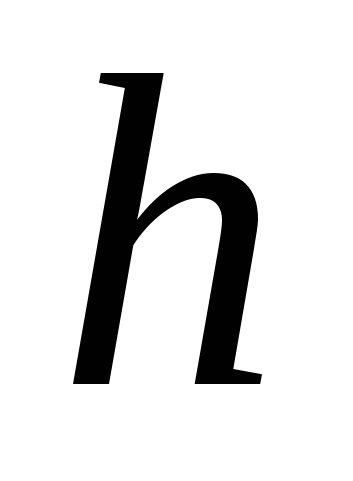 , м , м
|
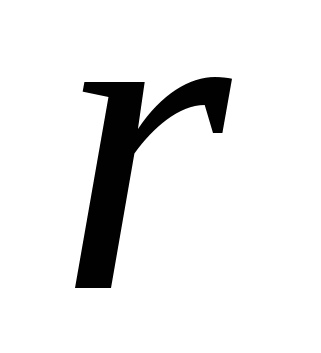 , м , м
|
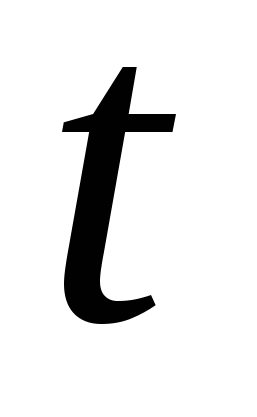 , с , с
|
 , ,
м/с2
|
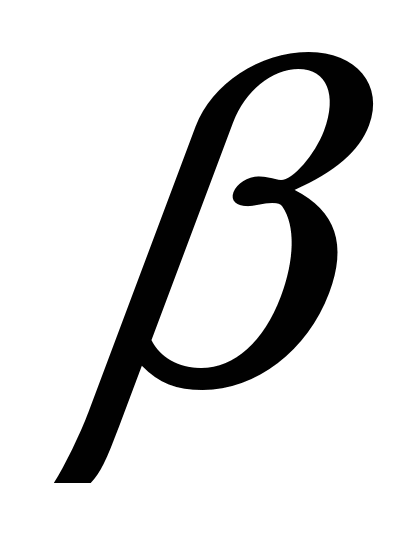 , ,
рад/с2
|
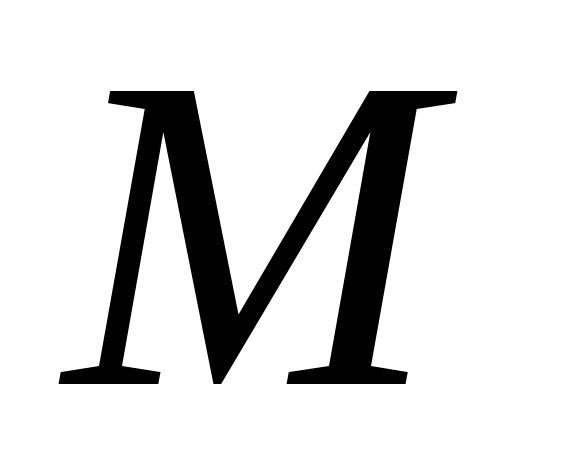 , ,
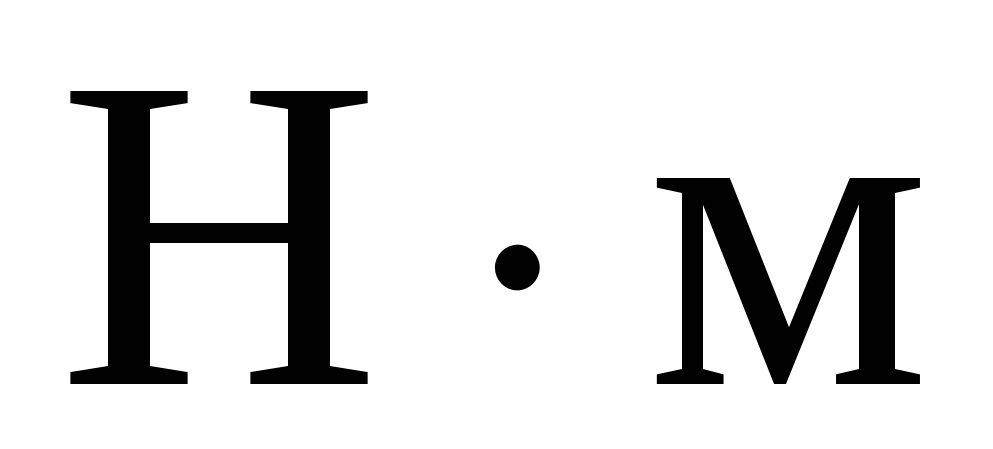
|
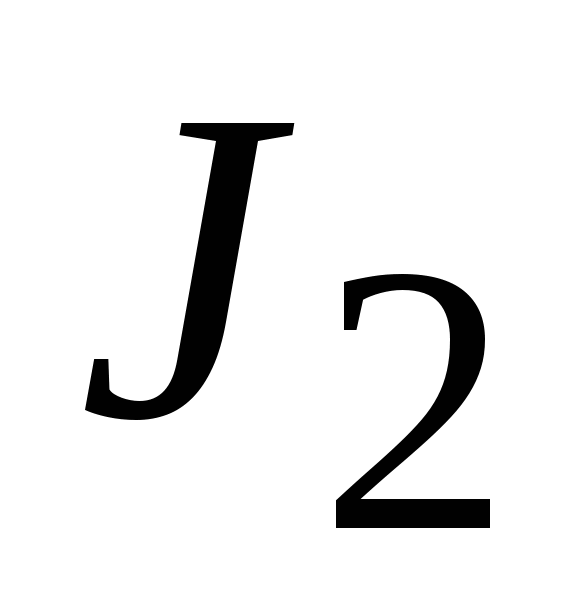 , ,
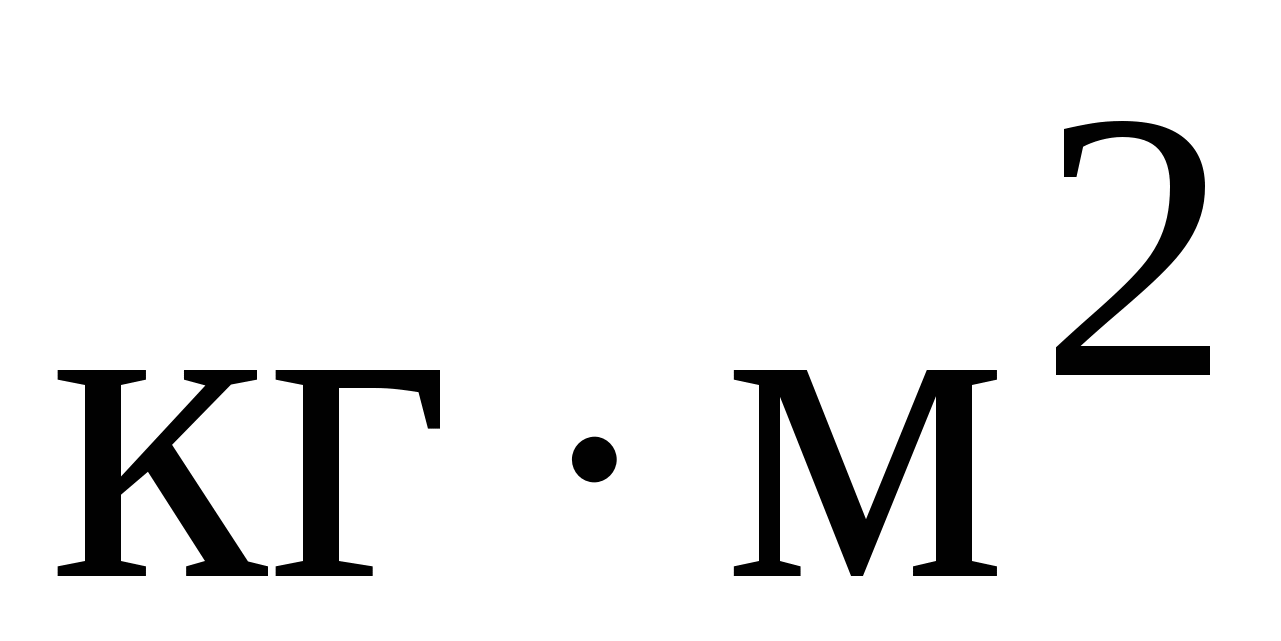
|
∆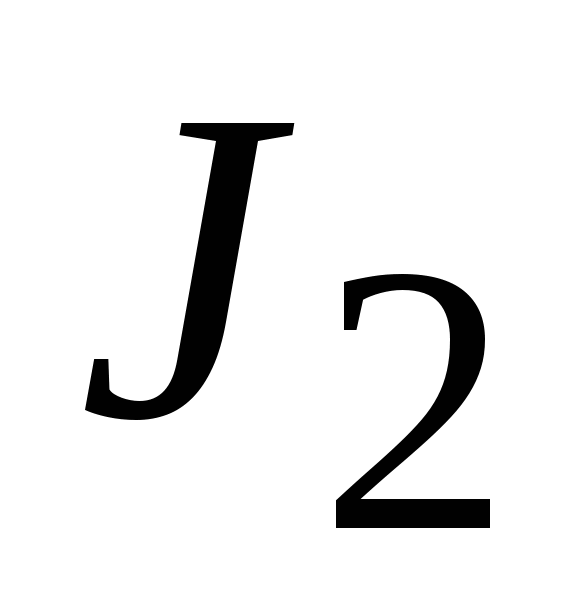 , ,
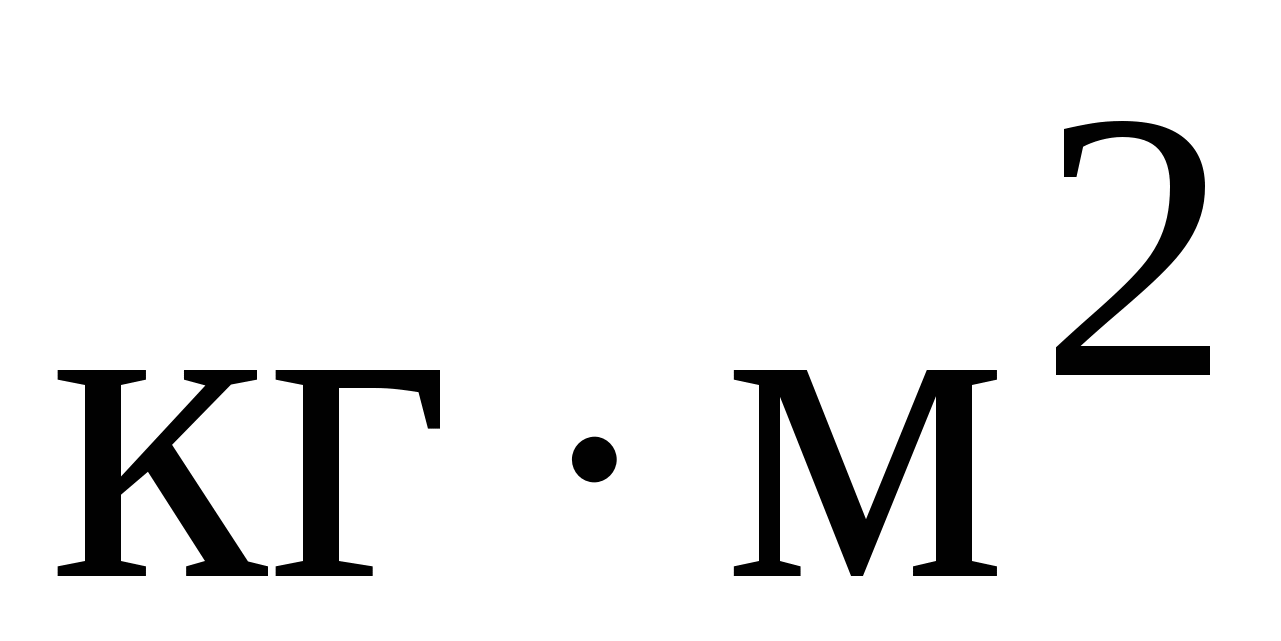
|
σ,
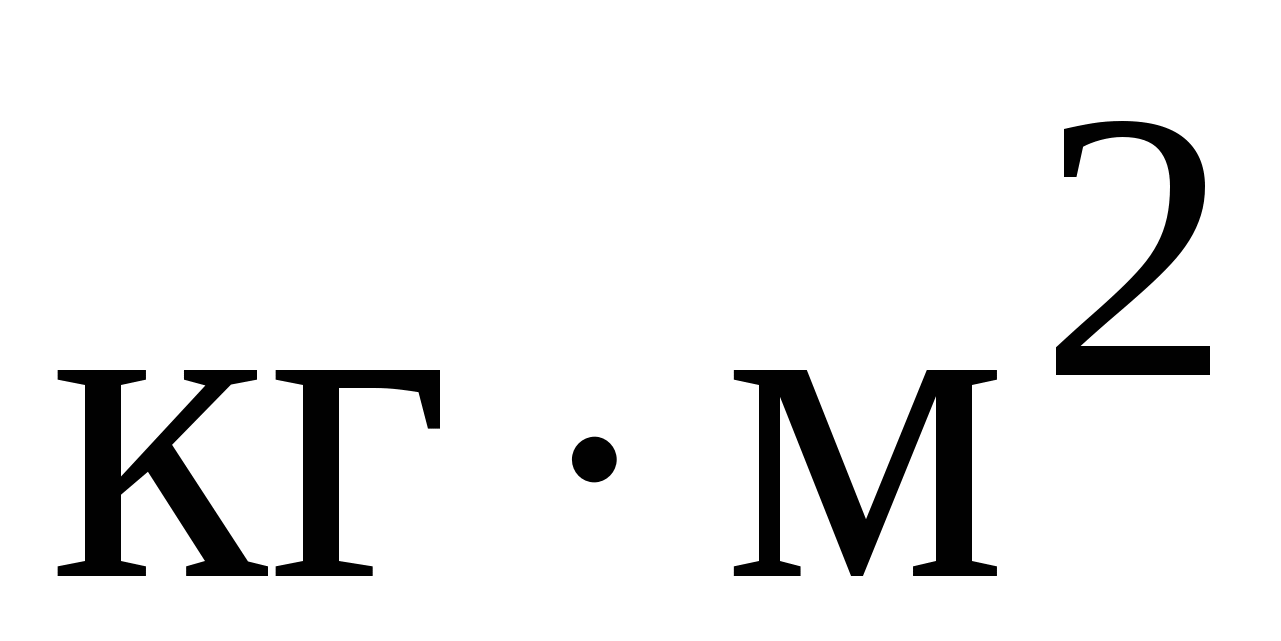
|
|
1
2
3
|
|
|
|
|
|
|
|
|
|
Средние значения
|
|
|
|
|
Оценить погрешность измерений и запишите результаты в виде
J
1=J
1ср±2σ.
J
2=J
2ср±2σ.
Найти отношения 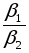 и
и 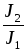 и проверить справедливость соотношения (27).
и проверить справедливость соотношения (27).
Сравнивая значения 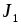 и
и 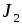 , сделать вывод о том, как момент инерции маятника зависит от распределения его массы по отношению к оси вращения.
, сделать вывод о том, как момент инерции маятника зависит от распределения его массы по отношению к оси вращения.
КОНТРОЛЬНЫЕ ВОПРОСЫ
Проверьте аналогию между величинами, характеризующими поступательное и вращательное движение, составив таблицу соответствия
Примечание: 1) таблица заполняется обязательно при оформлении отчета;
2) необходимо знать определение направления векторных величин.
Между какими величинами устанавливает связь основной закон динамики вращательного движения? Сформулируйте его.
Как определяется величина и направление моментов сил? В каких единицах измеряется эта величина?
От чего зависит момент инерции  , в каких единицах измеряется? Как понимать, что момент инерции величина аддитивная? Из чего состоит момент инерции маятника Обербека?
, в каких единицах измеряется? Как понимать, что момент инерции величина аддитивная? Из чего состоит момент инерции маятника Обербека?
Сделайте вывод формулы момента инерции цилиндра относительно оси, совпадающей с его осью симметрии.
Сформулируйте теорему Штейнера. Для чего она используется в работе?
Опираясь на схему установки, получите формулу, с помощью которой рассчитывали момент инерции маятника (24).
В ходе каких измерений мы убедились в зависимости момента инерции маятника от расстояния, на котором располагаются цилиндры относительно оси вращения и массы маятника?
В ходе каких измерений мы убедились в независимости момента инерции маятника от сил, приводящих в его вращению?
 Скачать 0.67 Mb.
Скачать 0.67 Mb.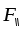 (силой, параллельной оси
(силой, параллельной оси 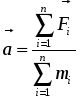 , (13)
, (13)