Л4 - Изучение развития электрического разряда в диэлектриках. Изучение развития электрического разряда в диэлектриках
 Скачать 240.47 Kb. Скачать 240.47 Kb.
|
|
2 Growth – выбор этого пункта начинает процесс моделирования, который можно прервать в произвольный момент времени нажатием любой клавиши и попасть в главное меню после подтверждения о прекращении процесса моделирования. 3 Inspector – позволяет просматривать (инспектировать) текущие значения в конкретной точке моделируемого промежутка. При выборе этого пункта меню в первом окне появляется курсор, который перемещается стрелками на клавиатуре, а в нижнем левом углу экрана отображается окно «Data Inspector», в котором выводятся значение следующих параметров в точке, на которой находится курсор: координаты точки, потенциал (Potenial), напряженность электрического поля E (Field), плотность сводных зарядов (Free Charge), плотность полного заряда (Total Charge), проницаемость диэлектрика (Permittivity) и проводимость канала (Conductivity), если курсор находится на разрядной структуре. 4 Print – вывод содержимого экрана на принтер (в черно-белом варианте, см. «Drawing BW»). Возможна печать в черновом (Draft), нормальном (Normal), уменьшенном (Little) режимах для матричных и струйных принтеров и на лазерном принтере (Laser). Information – получение информации о программе, методе и разработчиках. 6 Drawing BW – просмотр вида черно белого изображения, которое будет выведено на принтер при выборе в главном меню пункта «Print». Здесь задаются следующие параметры: процент от максимальной проводимости, выше которого каналы будут рисоваться толстыми линиями (Criterion for drawing), число силовых линий в первом и число эквипотенциальных линий (Number izoline) втором окнах. 7 Quit – выход из программы. По каждому пункту меню можно получить короткую информацию нажав клавишу F1. Под главным меню выведены параметры модели, с которыми в данный момент производится расчет: Needle length - длина острия (L); Applay voltage - приложенное напряжение (V); Growth exponent - показатель роста (); Threshold field - критическая напряженность поля (Ec); Time constant - временной параметр (); Size X, Size Y - размер моделируемого промежутка по X и по Y (в узлах решетки); Trans. parameter - параметр наследования проводимости вновь образованным каналом; Inc. param - параметр увеличения проводимости канала (); Decay parameter - параметр уменьшения проводимости канала; Init. Conduct. - начальная проводимость канала, инициированного с острия. Справа выводятся текущие значения числа пробитых точек (DS Site) и физического времени развитии разряда (time). Ниже расположены три окна, в которых отображается следующая информация: в первом окне (окна нумеруются слева направо) отображается напряженность поля в межэлектродном промежутке и распределение плотности свободных зарядов в разрядной структуре, значение которых можно определить с помощью цветовой палитры, расположенной слева от окна и максимального и минимального значений, выведенных под окном; во втором окне отображается распределение потенциала в межэлектродном промежутке; в третьем окне отображается проводимость каналов разрядной структуры. Под окнами выводятся три графика (рис 11): зависимость ln r от lnN; зависимость Q от t; зависимость l от t. где N - число пробитых узлов, попавших в окружность радиуса r и центром на кончике острия верхнего электрода, Q - общий заряд, t - текущее время развития пробоя, l - максимальная длина канала структуры разряда. 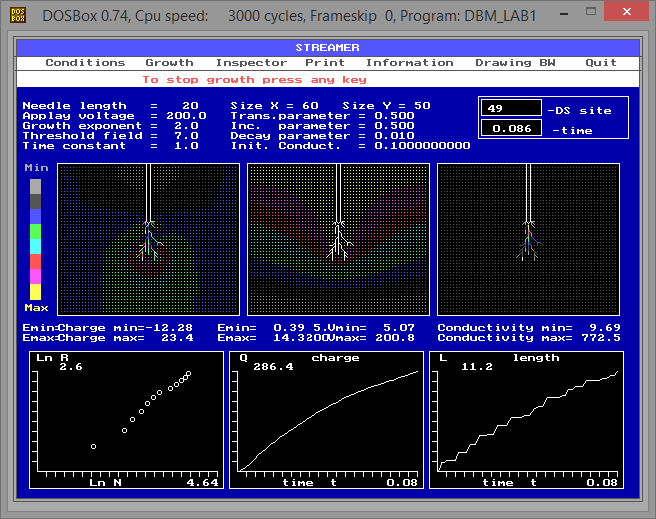 Рис. 11 – Интерфейс программы во время моделирования 3.2 Порядок выполнения работы Задание №1 Исследование влияния величины приложенного напряжения V на характер и время развития разряда в диэлектрике. 1.1 Запустите программу и введите следующие параметры диэлектрика Ec = 4; = 2; = 1; =0.5 и условия пробоя V и l (табл. 11). 1.2 Рассчитайте и занесите в табл. 2 среднюю напряженность поля в Eср промежутке Eср = V/d, где d = 50 - L - длина разрядного промежутка. 1.3 После расчета начального распределения поля, с помощью «инспектора», определите и занесите в таблицу №2 максимальную напряженность поля Emax. 1.4 Рассчитайте и занесите в табл. 1 коэффициент неоднородности поля k=Emax/Eср. 1.5 Распечатайте на принтере начальную конфигурацию поля. 1.6 Начните моделирование развития разрядной структуры. После завершения пробоя занесите в табл. 2 значения максимальной проводимости каналов max и времени развития разряда tр. 1.7 Распечатайте на принтере картину разряда и конфигурацию поля. 1.8 По графику зависимости логарифма числа пробитых узлов lnN от логарифма расстояния до острия lnr оцените фрактальную размерность D. Результаты занесите в таблицу №2. 1.9 Повторите действия п.п. 1.2 – 1.8 для следующих значений приложенного напряжения V = 205 и V= 210, при одинаковых значениях остальных величин. 1.10 Проанализируйте результаты исследования и напишите выводы. Таблица 1 – Условия пробоя
Таблица 2 – Результаты моделирования
Задание №2 Исследование влияния проводимости разрядных каналов на характер развития разряда и распределение поля в диэлектрике. 2.1 Запустите программу и введите следующие параметры диэлектрика: Ec = 4, =2, = 1, =0.5 и условия пробоя V и l (табл. 11). 2.2 Рассчитайте и занесите в табл. 3 среднюю напряженность поля в Eср промежутке Eср=V/d, где d = 50 - L - длина разрядного промежутка. 2.3 После расчета начального распределения поля, с помощью «инспектора», определите и занесите в табл. 3 максимальную напряженность поля Emax. 2.4 Рассчитайте и занесите в табл. 3 коэффициент неоднородности поля k = Emax/Eср. 2.5 Распечатайте на принтере начальную конфигурацию поля. 2.6 Начните моделирование развития разрядной структуры. 2.7 Прервите моделирование, когда разрядная структура достигнет половины разрядного промежутка. 2.8 С помощью инспектора определите напряженность поля у головки разрядных каналов Eг и в пространстве между каналами Eк. Результаты измерений занесите в табл. 4. 2.9 Продолжите моделирование развития разряда до завершения пробоя. Занесите в табл. 4 значения максимальной проводимости каналов max и времени развития разряда tр. Распечатайте на принтере картину разряда и конфигурацию поля. 2.11 По графику зависимости логарифма числа пробитых узлов lnN от логарифма расстояния до острия lnr оцените фрактальную размерность D. Результаты занесите в табл. 4. 2.12 Повторите действия п.п. 2.6 – 2.11 для параметров возрастания проводимости = 0.40 и = 0.59, при одинаковых значениях остальных величин. 2.13 Проанализируйте результаты исследования и напишите выводы. Таблица 3 – Условия пробоя
Таблица 4 – Результаты моделирования
Задание №3 Исследование влияния диэлектрического барьера на характер развития разряда и распределение поля в диэлектрике. 3.1 Запустите программу и введите следующие параметры диэлектрика: Ec = 4, = 2, = 1, =0.5 и условия пробоя V и l (табл. 11). 3.2 Введите в межэлектродный промежуток между острием и нижним электродом барьер с диэлектрической проницаемостью б = 10. 3.3 Рассчитайте и занесите в табл. 6 среднюю напряженность поля в Eср промежутке Eср = V/d , где d = 50 - L - длина разрядного промежутка. 3.4 После расчета начального распределения поля, с помощью «инспектора», определите и занесите в табл. 6 максимальную напряженность поля Emax. В табл. 5 внесите координаты расположения барьера. 3.5 Рассчитайте и занесите в табл. 5 коэффициент неоднородности поля k = Emax/Eср. 3.6 Определите и занесите в табл. 6 начальную напряженность поля в барьере Eб. 3.7 Распечатайте на принтере начальную конфигурацию поля. 3.8 Начните моделирование развития разрядной структуры. После завершения пробоя занесите в табл. 6 значение времени развития разряда tр. 3.9 Распечатайте на принтере картину разряда и конфигурацию поля. 3.10 Повторите действия п.п. 3.2-3.9 для значений диэлектрической проницаемости барьера б = 15 и б = 25, при одинаковых значениях остальных величин и расположении барьера. 3.11 Проанализируйте результаты исследования и напишите выводы. Таблица 5 – Условия пробоя
Таблица 6 – Результаты моделирования
Задание №4 Исследование влияния положительно заряженного включения на характер развития разряда и распределение поля в диэлектрике. 4.1 Запустите программу и введите следующие параметры диэлектрика: Ec = 4, = 2, = 1, = 0.5 и условия пробоя V и l (табл. 11). 4.2 Введите в межэлектродный промежуток перед острием круглое заряженное включение с плотностью свободных зарядов = 1 и внесите в табл. 7 координаты включения. 4.3 Рассчитайте и занесите в табл. 8 среднюю напряженность поля в Eср промежутке Eср = V/d , где d = 50 - L - длина разрядного промежутка. 4.4 Рассчитайте и занесите в табл. 7 коэффициент неоднородности поля k = Emax/Eср. 4.5 Распечатайте на принтере начальную конфигурацию поля. 4.6 Начните моделирование развития разрядной структуры. После завершения пробоя занесите в табл. 8 значение времени развития разряда tр и минимальное отклонение r0 структуры разряда от включения. 4.7 Распечатайте на принтере картину разряда и конфигурацию поля. 4.8 Повторите действия п.п. 4.2-4.7 для значений для значений плотности свободных зарядов включения = 2 и = 4, при одинаковых значениях остальных величин и расположении включения. 4.9 Проанализируйте результаты исследования и напишите выводы. Таблица 7 – Условия пробоя
Таблица 8 – Результаты моделирования
Задание №5 Исследование влияния диэлектрического включения на характер развития разряда и распределение поля в диэлектрике. 5.1 Запустите программу и введите следующие параметры диэлектрика: Ec = 4, = 2, = 1, = 0.5 и условия пробоя V и l (табл. 11). 5.2 Введите в межэлектродный промежуток в стороне от острия круглое диэлектрическое включение с диэлектрической проницаемостью в = 10 и внесите в табл. 9 координаты включения. 5.3 Рассчитайте и занесите в табл. 10 среднюю напряженность поля в Eср промежутке Eср = V/d , где d = 50 - L - длина разрядного промежутка. 5.4 Рассчитайте и занесите в табл. 9 коэффициент неоднородности поля k = Emax/Eср. 5.5 Распечатайте на принтере начальную конфигурацию поля. 5.6 Начните моделирование развития разрядной структуры. После завершения пробоя занесите в табл. 10 значение времени развития разряда tр и минимальное отклонение r0 структуры разряда от включения. 5.7 Распечатайте на принтере картину разряда и конфигурацию поля. 5.8 Повторите действия п.п. 5.2-5.7 для значений для значений диэлектрической проницаемости включения в = 20 и в = 30, при одинаковых значениях остальных величин и расположении включения. 5.9 Проанализируйте результаты исследования и напишите выводы. Таблица 9 – Условия пробоя
Таблица 10 – Результаты моделирования
Таблица 11 – Значения длины острия и напряжения
4 КОНТРОЛЬНЫЕ ВОПРОСЫ Что такое электрический пробой? Какими факторами определяется электрическая прочность диэлектрика? На какие стадии можно разделить процесс пробоя, каковы их отличительные особенности? Какие неустойчивости приводят к зарождению и развитию разрядных каналов в диэлектрике? Чем количественно характеризуются эти неустойчивости? Каковы причины стохастичности разряда? Как влияет величина приложенного напряжения V на характер развития разряда? Как влияет величина коэффициента неоднородности поля и перенапряжения на характер развития разряда? Что такое фрактал? Приведите примеры фрактальных структур и процессов, приводящих к их формированию? Что такое фрактальная размерность и как можно ее определить? Какими свойствами обладают фрактальные структуры? Как влияет увеличение проводимости разрядных каналов на распределение электрического поля и на характер развития разряда? Каковы изменения распределения электрического поля и характера развития разряда при увеличении диэлектрической проницаемости барьера? Как влияет заряд и диэлектрическая проницаемость включений на траекторию разрядных каналов? СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ Смирнов Б.М. Физика фрактальных кластеров. - М.: Наука, 1991. - 136 с. Федер Е. Фракталы. - М.: Мир, 1991. - 254 с. Сканави Г.И. Физика диэлектриков. (Область сильных полей). - М.: ГИФМ, 1958. - 907 с. Бонч-Бруевич В.Л., Звягин И.П., Миронов А.Г. Доменная электрическая неустойчивость в полупроводниках. - М,: Наука, 1972. Niemeyer L., Pietronero L., Wiesman H.J. Fractal dimension of dielectric breakdown. - Phys. Rev. Lett., 1984, vol. 52, p. 1033-1036. Кухта В.Р., Лопатин В.В., Носков М.Д. Применение фрактальной модели к описанию развития разряда в конденсированных диэлектриках. - ЖТФ, 1995, т. 65, вып. 2, с.63-75. |
