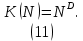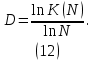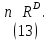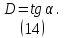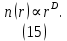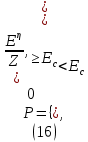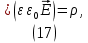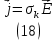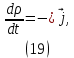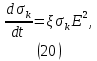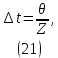|
|
Л4 - Изучение развития электрического разряда в диэлектриках. Изучение развития электрического разряда в диэлектриках
2 ОСНОВЫ ФРАКТАЛЬНОГО ПОДХОДА
Изучая различные встречающиеся в природе явления и объекты, мы прежде всего описываем их геометрическую форму. При этом обычно используем понятия евклидовой геометрии: прямые, плоскости, окружности, сферы и т.д. Однако многие процессы, протекающие в природе, приводят к образованию структур, для описания которых недостаточно обычной геометрии. Возьмем примеры из природы: горы, реки, береговые линии, облака, деревья. Их сложно описать с помощью прямых линий, плоскостей, сфер и т.д. Отличительной особенностью этих объектов является самоподобие, т.е. часть объекта подобна целому. Например, геометрия притока реки подобна геометрии всей реки. Рассматривая самоподобный объект во все увеличивающихся масштабах, мы будем выявлять все более тонкие детали его структуры, а вновь выявленная структура будет подобна той, что можно видеть в более мелком масштабе. Обладающие такими свойствами объекты называют фракталами. (Термин «фрактал», от латинского слова «fractus» - изломанный, был введен в науку в 1975 г. Б. Мандельбратом). В последние годы понятие фрактал стало широко распространенным в разных областях науки: в физике, химии, биологии, социологии и т.д. Фрактальные свойства обнаружены у множества объектов. Молекулы белков и скопление звезд в космосе, структуры кровеносных сосудов человека и поверхности разломов стали, турбулентные течения, электрические разряды и т.д. – все эти различные по своей природе структуры обладают фрактальными свойствами.
Мы определили фрактал, как структуру, которая состоит из частей, которые в каком-то смысле подобны целому. Количественно фрактальная структура характеризуется значением фрактальной размерности. Определим понятие фрактальной размерности, как размерности подобия. Рассмотрим в качестве примера одномерный объект – отрезок (рис. 3а). Если разделить отрезок на N равных частей (рис. 3б), то мы увидим, что он состоит из N своих копий уменьшенных в N раз.

Рис. 3 – Одномерный объект
Если мы будем разбивать на части двумерный объект – квадрат, то увидим, что он состоит из N2 своих копий уменьшенных в N раз (рис. 4а). Трехмерный куб состоит уже из N3 своих копий уменьшенных в N раз (рис. 4б). Таким образом, если D мерный объект состоит из К(N) своих копий уменьшенных в N раз, то выполняется соотношение
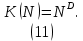
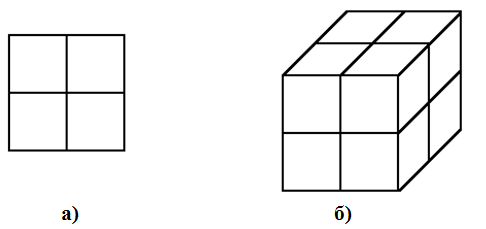
Рис. 4 – Двумерный (а) и трехмерный (б) объекты
Из этого соотношения можно выразить размерность объекта.
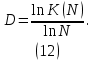
Теперь попытаемся построить объект, имеющий дробную размерность. Построение будем проводить по шагам. Пусть на нулевом шаге n = 0 имеется отрезок длиной L0 (рис. 5 а). На первом шаге заменяем исходный отрезок тремя отрезками длины L1 = L0/2, расположенными друг относительно друга, как показано на рис. 5 б. На втором шаге, каждый из новых отрезков длиной L1 заменяем тремя отрезками длиной L2 = L1/2 (рис. 5 в). Аналогичным образом выполняются третий и четвертый шаги (рис. 5 г, д). Мысленно продолжая описанную процедуру до бесконечности, получим самоподобный объект, который состоит из трех своих копий, уменьшенных в два раза. Следовательно, ему можно сопоставить дробную размерность D равную ln 3/ln 2 1,585. Построенный таким образом объект является геометрическим фракталом. Так же, как и любой объект геометрии, он «идеализирует» действительность. Реальные физические фрактальные объекты, такие, как например, фрактальные кластеры (агрегаты, образующиеся при слипании микроскопических частиц), являются самоподобными только статистически. К тому же они всегда имеют некоторый минимальный и максимальный размер. Поэтому, можно говорить о фрактальности реальных объектов только в определенном диапазоне масштабов: от минимального до максимального.
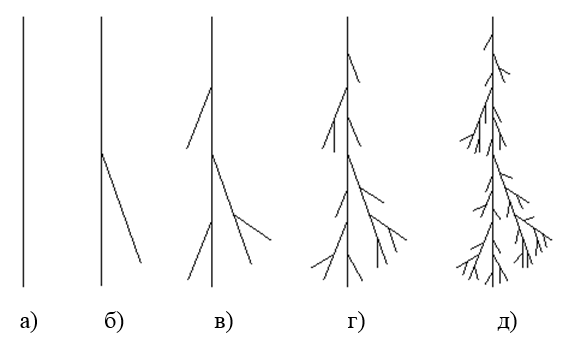
Рис. 5 – Фрактальный объект
Экспериментально фрактальную размерность можно определить, изучая зависимость числа элементов, составляющих фрактальную структуру, от ее размера. Рассмотрим сначала одномерную структуру, например, линейную цепочку частиц длиной R (рис. 6). Очевидно, что число частиц в таком объекте n пропорционально размеру R (n
R). Если частицы образуют двумерный объект – диск, то n
R2. Для трехмерного объекта n
R3. Тогда для фрактальной структуры с дробной размерностью D выполняется соотношение
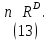
Следовательно, число элементов из которых состоит фрактал, пропорционально его размеру в степени D, где D - фрактальная размерность объекта.
Таким образом, чтобы определить размерность фрактальной структуры, необходимо построить в двойном логарифмическом масштабе график зависимости числа элементов, составляющих фрактал, от его размера R. Полученная зависимость аппроксимируется прямой линией, тангенс угла наклона которой будет равен фрактальной размерности (рис. 7):
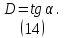
Таким образом, мы ввели понятие фрактала, дали определение фрактальной размерности D, рассмотрели метод ее вычисления. Все это составляет геометрическую основу фрактального подхода к изучению различных физических явлений. Физика фракталов изучает связь между фрактальной геометрией и физическими свойствами природных явлений. Мы будем применять методы физики фракталов для изучения структуры разрядных каналов, возникающих при пробое диэлектрика.
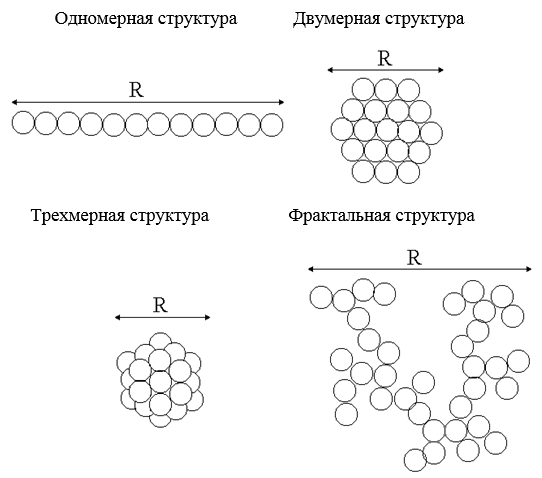
Рис. 6 – Многомерные фрактальные структуры
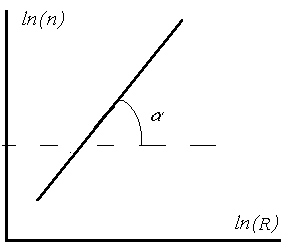
Рис. 7 – Зависимость числа элементов от размера фрактала
С помощью понятий фрактальной геометрии можно не только качественно, но и количественно описать стохастические структуры разрядных каналов, подобные изображенным на рис. 1. Кустообразная структура, рис. 1б, плотно заполняет пространство, т.е. можно сказать, что она имеет размерность равную трем и, следовательно, не является фракталом. В отличие от нее древовидная структура, рис. 1а, самоподобна и обладает фрактальными свойствами. Фрактальную размерность D такой структуры можно определить, используя вытекающее из формулы (14) соотношение между полной длиной n(r) всех разрядных каналов, заключенных в сфере радиуса r с центром в начале структуры, и величиной r,
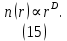
Из выражения (15) следует, что фрактальная размерность D будет равна тангенсу угла наклона прямой, аппроксимирующей график зависимости ln n от ln r. Измеренная таким способом фрактальная размерность D структуры, изображенной на рис. 1а равна примерно 1,8.
Фрактальная размерность развивающихся при пробое разрядных структур зависит от свойств диэлектрика и вида прикладываемого напряжения. Например, анализ экспериментальных данных показывает, что величина фрактальной размерности увеличивается с повышением напряжения. Следовательно фрактальная размерность разрядной структуры связана с происходящими при пробое процессами. Поэтому определение фрактальной размерности имеет важное значение для полного понимания физики пробоя диэлектриков.
2.1 Фрактальная модель роста разрядной структуры
2.1.1 Описание модели
Фрактальная модель развития разряда основана на совместном рассмотрении как стохастических, так и детерминистических процессов. Детерминистические закономерности используются для определения распределения электрических полей, зарядов, токов в диэлектрике, а стохастические - для описания роста разрядных каналов. Необходимость применения стохастических закономерностей связана с определяющей ролью неустойчивостей в развитии разрядных каналов. В результате развития любой неустойчивости микроскопические флуктуации параметров диэлектрика быстро нарастают по величине и приводят к стохастическому росту разрядных каналов. Развитие всех типов неустойчивостей определяется в первую очередь напряженностью электрического поля. Поэтому вероятность формирования канала P в том или ином месте должна зависеть от локальной напряженности поля Eл. Вид функции, выражающей эту зависимость, может быть установлен путем анализа микроскопических процессов, приводящих к неустойчивостям, или с помощью сравнения результатов моделирования с экспериментальными данными. В качестве первого приближения можно принять, что вероятность роста P пропорциональна E, если напряженность поля больше некоторой критической напряженности Ec, и равна нулю, если E < Ec:
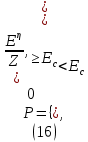
где Z = E – нормирующий множитель, величина которого определяется из условия нормировки: сумма вероятностей по всем направлениям роста каналов должна быть равна единице P = 1. Введение в формулу (16) критической напряженности Ec означает, что развитие неустойчивостей и формирование каналов не происходит, если напряженность поля меньше некоторого порогового значения. Величина Ec зависит от свойств диэлектрика.
Показатель степени , определяющий связь вероятности роста с напряженностью поля, можно рассчитать по законам квантовой механики и статистической физики для конкретного вида неустойчивости. Развитие всех неустойчивостей определяется энергией электрического поля. Предположив, что вероятность роста канала P связана с плотностью энергии электрического поля 0E2/2, можно сделать вывод, что значение должно быть близко к двум.
Напряженность электрического поля в диэлектрике рассчитывается с помощью теоремы Гаусса:
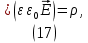
где – плотность свободных зарядов. Распределение свободных зарядов и электрического поля изменяется в процессе развития пробоя. Поскольку проводимость разрядных каналов значительно выше проводимости диэлектрика, движением зарядов в диэлектрике можно пренебречь. Динамика зарядов в разрядной структуре описывается законом Ома:
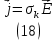
и уравнением непрерывности:
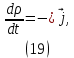
здесь k – проводимость разрядных каналов, j – плотность тока.
Проводимость разрядных каналов k растет пропорционально выделяющейся в них энергии. Изменение проводимости можно определить, например, по формуле Ромпе-Вейцеля:
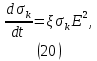
где - параметр увеличения проводимости.
Таким образом, во фрактальной модели пробоя рост разрядных каналов описывается стохастически соотношением (17), а динамика распределения электрических полей и зарядов определяется детерминистическими законами, формулы (18-20).
2.1.2 Численная реализация модели
Для проведения компьютерного моделирования фрактальная модель реализована как дискретный алгоритм роста на двухмерной решетке. Развитие разряда рассматривается в геометрии острие-плоскость. Диэлектрик, находящийся между электродами, описывается квадратной решеткой, рис. 8. Рост разрядной структуры начинается с острия и происходит по шагам. За один временной шаг структура растет на одно ребро или диагональ решетки. Вероятность того, что пробой произойдет по некоторому ребру или диагонали, соединяющей уже принадлежащий структуре разряда и еще не пробитый узел, зависит от локальной напряженности поля между ними (разности потенциалов между этими узлами, деленной на расстояние между ними) согласно соотношению (17).
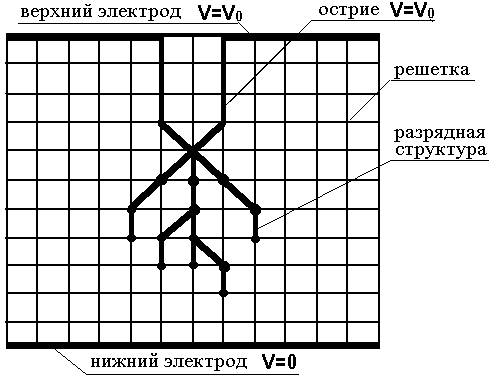
Рис. 8 – Геометрия электродов, используемая для моделирования
Распределение электрического потенциала и зарядов на решетке находится с помощью конечно-разностной формы уравнений (17) – (20). Граничными условиями являются потенциалы электродов: потенциал острия V0, а потенциал нижнего электрода равен нулю.
Динамика движения зарядов и изменение проводимости разрядных каналов определяются согласно формулам (18) – (20) в дискретной форме. Величина интервала физического времени t, соответствующая данному шагу моделирования, определяется распределением вероятностей роста (16). Используя теорию вероятностей, можно показать, что значение t обратно пропорционально величине нормирующего множителя Z:
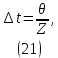
где – является параметром перехода к физическому времени.
Таким образом работа программы сводится к последовательному выполнению следующих процедур на каждом шаге роста:
расчет электрического потенциала по теореме Гаусса (17);
определение места роста канала и интервала физического времени, соответствующего данному шагу, в соответствии с распределением вероятности (16);
расчет изменения распределения зарядов согласно закону Ома (18) и уравнению непрерывности (19);
определение изменения проводимости каналов согласно формуле Ромпе-Вейцеля (20).
Результат моделирования зависит от условий пробоя (напряжение V, длина острия L) и параметров (Ec, , , ), описывающих свойства диэлектрика. Параметры времени и увеличения проводимости определяют скорость нарастания проводимости разрядных каналов. Увеличение и приводит к росту проводимости и уменьшению падения напряжения вдоль разрядных каналов. Напряженность поля на концах разрядных каналов увеличивается, а между одновременно развивающимися каналами уменьшается. В результате этого разрядная структура становится менее ветвистой (фрактальная размерность D уменьшается).
Увеличение значения критической напряженности Еc приводит к сокращению числа возможных путей роста разрядной структуры и, следовательно, к уменьшению ветвистости структуры разряда (D 1). Если критическая напряженность Еc превосходит локальную напряженность во всех точках, то развитие разряда прекращается, и мы имеем незавершенный пробой. Параметр η определяет зависимость вероятности роста от величины локальной напряженности поля. При η= 0 рост равновероятен для всех разрешенных направлений. В результате будет образовываться плотная структура, полностью заполняющая пространство (D = 2). При больших значениях параметра η
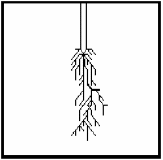
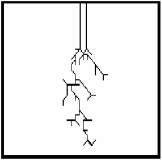
(η >> 1) рост будет происходить только в направлении с наибольшей напряженностью поля. При этом будет возникать линейная структура (D = 1). При значениях параметра η порядка единицы в процессе роста образуются ветвящиеся структуры, размерность D которых зависит от величины η. На рис. 9 изображены картины разряда, полученные для значений параметра η, равных 1 и 3 соответственно, при прочих равных условиях.
|
|
а) при η = 1
|
б) при η = 3
|
Рис. 9 – Результат моделирования
3 СОДЕРЖАНИЕ РАБОТЫ
3.1 Описание программы
Программное обеспечение, созданное на базе фрактальной модели пробоя диэлектриков, реализовано на языке программирования Pascal и имеет «дружественный» графический интерфейс, позволяющий изменять параметры моделирования в широком диапазоне. Запуск исполняемого файла приводит к появлению на экране заставки, которая исчезает после нажатия любой клавиши или по истечению некоторого времени. После чего отображается рабочий экран, состоящий из главного меню, списка текущих параметров моделирования, окон отображающих картину пробоя и графиков (выводятся после начала счета). Изменение параметров моделирования, просмотр текущих значений в моделируемой области и управление программой производятся через главное меню, находящееся в верхней части рабочего экрана.
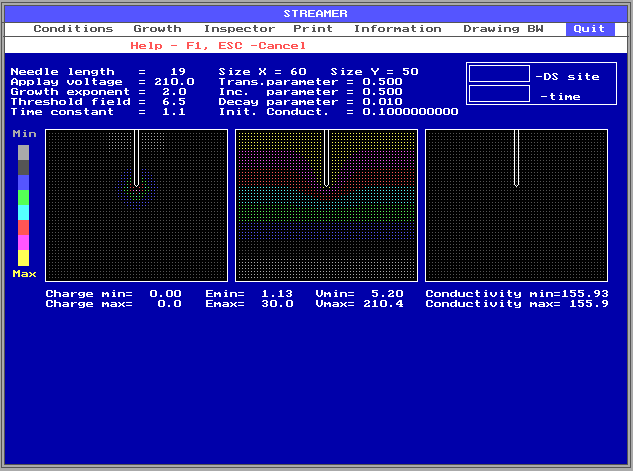
Рис 10 – Графический интерфейс программы
Главное меню состоит из семи пунктов:
1Conditions – ввод параметров модели, при выборе которого появляется вертикальное подменю, содержащее пять следующих пунктов:
1.1 Condition - после выбора этого пункта запрашивается подтверждение ввода новых параметров, в случае положительного ответа вы можете изменять длину острия L (Needle length) и значение приложенного напряжения V (Applied voltage). После чего производится пересчет поля с новыми условиями пробоя.
1.2 Dielectric – выбор этого пункта позволяет вам изменять следующие параметры: показатель роста (Growth exponent), критическую напряженность поля Ес (Threshold field), и временной параметр (Time parameter).
1.3 Channals – позволяет внести изменение параметра увеличения проводимости канала (Increasing parameter).
1.4 Inclusion - после выбора этого пункта появляется следующее меню, позволяющее выбрать форму включения (New rectangle - прямоугольник, New ellipse - эллипс), а также редактировать уже введенные включения (Edit). При выборе первых двух пунктов в среднем окне появляется курсор. Перемещая курсор стрелками на клавиатуре выберите левую верхнюю вершину области включения и зафиксируйте ее нажатием клавиши «Enter». Аналогичным образом выберите правую нижнюю вершину области включения (если форма включения - эллипс (New ellipse), то в выбранную прямоугольную область будет вписан эллипс). По окончанию ввода геометрии включения появляется окно, которое позволяет изменить значения плотности свободных зарядов (Add Charge) и проницаемости (Add Permittivity) в выбранной области, здесь вводится значение, на которое необходимо изменить соответствующий параметр (например нужно, чтобы включение обладало проницаемостью равной 20, для этого в поле «Add Permittivity» надо ввести 19. Так как сам диэлектрик обладает проницаемостью равной единице, то в результате 19 + 1 = 20 - проницаемость в выбранной области будет равно двадцати). После чего происходит пересчет полей. При выборе пункта «Edit» появляется окно «Inclusions list», в котором можно посмотреть введенные включения и их параметры, а также удалить ненужные.
1.5 Options – выбор этого пункта позволяет определить в каких окнах показывать введенные включения (Window1 [x], Window2 [x], Window3 [x]), по умолчанию включения отображаются во всех окнах, а также указать через сколько шагов роста выводить изменения графиков (Change). Во всех окнах ввода параметров указаны пределы их изменения.
|
|
|
 Скачать 240.47 Kb.
Скачать 240.47 Kb.