телетрафик. Изучение свойств и характеристик пуассоновского процесса

• Название: Изучение свойств и характеристик пуассоновского процесса
• Анкор: телетрафик
• Дата: 28.04.2021
• Размер: 65.84 Kb.
• Имя файла: телетрафик.docx
• Тип: Отчет; #199713

Минобрнауки России

Юго-Западный государственный университет
Кафедра космического приборостроения и систем связи

Отчёт по выполнению лабораторной работы №1 по курсу «Теория телетрафика»

на тему «Изучение свойств и характеристик пуассоновского процесса»

Выполнил: студент группы ИТ-81б

Носова В. И.
Вариант: 9

(подпись)

«»2021 г.

Проверил: преподаватель кафедры КПиСС

Чуев А.А

(подпись)

«»2021 г.


Курск 2021 г.

1 Цель работы

Изучить свойства и характеристики пуассоновского (простейшего) потока. Сравнить теоретические и модельные значения полученных характеристик.

2 Краткая теория

Простейший поток обладает следующими свойствами: стационарность, ординарность и отсутствие последействия.

Свойство стационарности означает, что с течением времени вероятностные характеристики потока не меняются.

Свойство ординарности означает практическую невозможность группового поступления требований.

Свойство отсутствия последействия означает независимость вероятностных характеристик потока от предыдущих событий.

3 Выполнение работы

Интенсивность поступления требования для варианта 9 равна 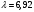треб/мин.

С помощью программы Microsoft Excel сгенерированы случайные равномерно распределённые числа r_i(0,1). Для этого использована функция СЛЧИСЛ().

Длины промежутков времени между последовательными требованиями потока равны: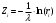

Исследуемы промежуток в соответствии с вариантом: [13;17]. Моменты поступления запросов находятся по формуле:

Полученные результаты внесены в таблицу 1.
Таблица 1 – Результаты полученные в ходе выполнения работы

Случайные переменные ri	Случайное значение Zi	Моменты поступления требования, tk
0,809374952	0,028199066	13,028199
0,992242707	0,001038338	13,029237
0,358954691	0,136607881	13,165845
0,633770306	0,060809158	13,226654
0,185199128	0,224843155	13,451498
0,394879977	0,123889789	13,575387
0,993224485	0,000906476	13,576294
0,652854961	0,056853371	13,633147
0,343850834	0,142339645	13,775487
0,62787951	0,062054266	13,837541
0,884570649	0,016353719	13,853895
0,070617446	0,353397074	14,207292
0,151565996	0,251564551	14,458856
0,224239934	0,199338489	14,658195
0,805918996	0,028769606	14,686965
0,81196611	0,02777289	14,714737
0,324419181	0,150095844	14,864833
0,44784798	0,107106858	14,97194
0,251303295	0,184145963	15,156086
0,944769859	0,007575189	15,163661
0,274357652	0,17244303	15,336104
0,44590954	0,107685223	15,44379
0,226693036	0,197887792	15,641677
0,45118205	0,106117915	15,747795
0,860042935	0,020103062	15,767898
0,911700246	0,012325869	15,780224
0,9135952	0,012049026	15,792273
0,297390048	0,161694761	15,953968
0,720943611	0,043625914	15,997594
0,189919392	0,221487407	16,219081
0,385513753	0,127090455	16,346172
0,289163761	0,165434947	16,511607
0,487357381	0,095834344	16,607441
0,499400454	0,092579599	16,700021
0,180093237	0,228570744	16,928591
0,765717292	0,0355923	16,964184

Интервал [13;17] разделён на 25 промежутков и определено количество требований, попавших в каждый промежуток, который равен τ= 0,16 мин. Данные значения занесены в таблицу 2.
Таблица 2 – Количество требований попавших в промежуток

№ интервала	1	2	3	4	5
XN(τ)	2	2	1	3	1
№ интервала	6	7	8	9	10
XN(τ)	2	0	1	0	1
№ интервала	11	12	13	14	15
XN(τ)	3	1	1	2	1
№ интервала	16	17	18	19	20
XN(τ)	1	1	4	2	0
№ интервала	21	22	23	24	25
XN(τ)	2	1	1	1	2

Из таблицы 2 определены параметры статистического распределения случайной величины и занесены в таблицу 3. n_k­ количество интервалов, в которое попало k требований.
Таблица 3 ­ Параметры статистического распределения случайной величины

Xk(τ)	0	1	2	3	4	5
nk	3	12	7	2	1	0

Математическое ожидание числа требований в k интервале равно: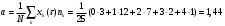
треб
Отсюда 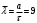треб/мин.

Вероятность поступления kтребований для модельного значения параметра потока находится по формуле 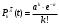(1).
(1)

Вероятность поступления k требований для заданного значения параметра потока находится по формуле 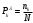(2).

(2)

Тогда:

а) Вероятность отсутствия требования P₀(t) за промежуток t=T₂-T₁.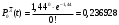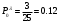



б) Вероятность поступления одного требования P₁(t).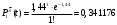




в) Вероятность поступления четырёх требований P₄(t).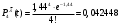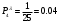




г) Вероятность поступления не менее пяти требований P_≥5(t) = 1 - (P₀+ P₁+ P₂+ P₃+P₄).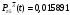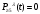





д) Вероятность поступления менее трёх требований P_<3(t) = P₀+ P₁+ P₂.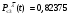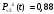



е) Вероятность поступления не более семи требований P_≤7(t) = P₀+ P₁+ P₂+ P₃+P₄ +P₅+ P₆+P₇.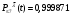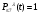





ж) Вероятность, что промежуток между требованием P[0,1 < z_k <0,5] = F(0,5) - F(0,1).

P[0,1 < z_k <0,5] = 0,191462461 - 0,039827837 = 0,151634624

4 Вывод

Сгенерировал случайные равномерно распределённые числа, вычислил интенсивность потока, на промежутке Т₁;Т₂ получил последовательность моментов поступления требований, провёл статистическую обработку полученных результатов, для каждого промежутка определить количество требований, определил параметры статистического распределения случайной величины, определил модельное значение параметра потока, для заданного и модельного значения определил вероятности отсутствия, поступления одного, четырёх, не менее пяти, менее трёх и не более семи требований, а так же вероятность, что промежуток между требованием (0,1;0,5).