моча съела гавно. распечатать. Изучение законов вращательного движения на маятнике обербека
 Скачать 39.94 Kb.
|
|
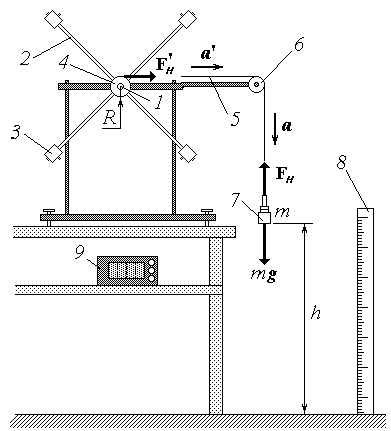
Лабораторная работа 1.3 ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА МАЯТНИКЕ ОБЕРБЕКА Цель работы 1) изучение кинематических и динамических характеристик вращательного движения; 2) экспериментальное определение момента инерции крестовины маятника Обербека и момента сил трения; 3) проверка справедливости закона сохранения (превращения) энергии механической системы. Схема экспериментальной установки
Fн = т(g – a) (1) Мн = т(g – a)R (2) J = Мн – Мтр , (3)  (4) (5)Wp = mgh; (6)  , (7) , (8)Атр = – Мтр, (9)  (10) (11) (12) (13) (14)Порядок измерений и обработки результатов 1. Ознакомьтесь с рекомендациями по выполнению работы на данной экспериментальной установке. Запишите в тетрадь рекомендуемое значение высоты h. 2. Освободив шкив от намотанной на него нити, измерьте штангенциркулем его диаметр. Рассчитайте радиус шкива R и, выразив его в метрах, также запишите в тетрадь. 3. Занесите во второй столбец таблицы значение массы груза т (в кг).
4. Вращая крестовину, намотайте нить на шкив (равномерно, одним слоем) так, чтобы нижняя поверхность груза 7 оказалась на заданной высоте h над полом. 5. Отпустив крестовину, одновременно включите секундомер, а в момент касания грузом пола – выключите. Запишите время падения в третий столбец таблицы. 6. Повторите пп. 4 и 5 с тем же грузом еще два раза. Рассчитайте и занесите в таблицу среднее из трех значений времени t. 7. Увеличивая массу груза согласно рекомендациям, выполните пп. 3-6 еще пять раз. 8. Для каждого из шести проделанных опытов рассчитайте ускорение а по формуле (4), подставляя в нее среднее из трех измеренных значений времени падения t. Величину а (с точностью не менее чем до трех значащих цифр) запишите в четвертый столбец таблицы. 9. По формулам (2) и (5) вычислите значения момента силы натяжения нити Мн и углового ускорения . Результаты занесите в соответствующие столбцы таблицы. 10. Руководствуясь правилами, изложенными в части I, постройте график зависимости углового ускорения от момента силы натяжения (в данной работе необходимо, чтобы начало координат совпадало с нулевыми значениями откладываемых величин и Мн). Нанесите на график экспериментально полученные точки. 11. Одним из описанных ниже способов* обработайте линейную экспериментальную зависимость (Мн) и найдите значения момента инерции крестовины J и момента сил трения Мтр. Запишите эти значения в тетрадь. 12. Для одного из проделанных опытов* рассчитайте по формулам (12)-(14) скорость груза v, угловую скорость вращения и угол поворота крестовины маятника Обербека в момент падения груза на пол. 13. Вычислите значения левой и правой частей уравнения закона сохранения энергии (11). Сравнив эти значения между собой, сделайте выводы. Обработка зависимости (Мн) Угловое ускорение крестовины и момент силы натяжения нитиМн связаны уравнением основного закона динамики вращательного движения (3). Как показано в части I (см. с. 22), зависимость (Мн) можно представить в виде  , (15)где  . Таким образом, определив коэффициенты линейной зависимости (15) Kиb, легко найти момент инерции J и момент сил трения Мтр : (16)Обработку экспериментальной зависимости (Мн) необходимо провести графическим методом. 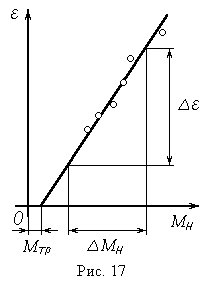 Графический способ. По экспериментальным точкам проведите сглаживающую прямую. Из уравнения (3) следует, что угловое ускорение обращается в нуль при Мн = Мтр . Таким образом, момент сил трения Мтр определяется (с учетом масштаба!) отрезком, отсекаемым проведенной прямой на оси абсцисс (см. рис.). Величина K в уравнении (15) представляет собой угловой коэффициент прямой, т.е. тангенс угла ее наклона к оси абсцисс. Согласно (16), момент инерции J есть величина, обратная K, – значит, его можно найти как котангенс этого угла. Выбрав на сглаживающей прямой две достаточно удаленные друг от друга точки, рассчитайте значение J как отношение отрезков  ,причем величины отрезков Мн и должны быть взяты с учетом масштаба графика и выражены в соответствующих единицах измерения: Мн – в Нм, а – в рад/с2 или в с – 2. Только в этом случае результат будет правильным, и момент инерции будет иметь размерность кгм2. ** По рекомендации преподавателя. |
