метрология умкд. БАРЖ УМКД А5 2020. Ж. А. Даев Бейсызыты автоматты басару жйелері Пніні ОУдістемелік кешені

• Название: Ж. А. Даев Бейсызыты автоматты басару жйелері Пніні ОУдістемелік кешені
• Анкор: метрология умкд
• Дата: 18.01.2021
• Размер: 1.39 Mb.
• Имя файла: БАРЖ УМКД А5 2020.doc
• Тип: Документы; #169173
• страница: 5 из 6

5. ПРАКТИКАЛЫҚ /СЕМИНАР САБАҚТАРДЫҢ ӘДІСТЕМЕЛІК НҰСҚАУЛАРЫ
1-ТАҚЫРЫП. Бейсызықты жүйелердің негізгі ерекшеліктері. Типтік бейсызықты сипаттамалар. Бейсызықты дифференциалдық теңдеулер
Практикалық сабақ жоспары:

1. Сабақтың басында көрсетілген мысалды талқылау.

2. Көрсетліген мысалдардағы әдістерді бекіту мақсатында берілген есептерді шығару.

3. Шығарылған есептердің шешімін талқылау.

4. Практикалық жұмыс бойынша есепті рәсімдеу және оларды оқытушыға тексеруге тапсыру.
Тапсырмалар:

Мысал №1. Тақырыптағы типтік бейсызықты сипаттамаларды зерттеуді VisSim бағдарламасы арқылы жасаймыз. VisSim пакетінің құрамында бар типтік бейсызықты элементтерді қарастырып зерттейміз. Бұл идеал реле, қанығу сипаттамасы, сезімталдық. Осы элементтердің бейнесіне әрқайсысында екі рет басу арқылы 0-ден артық сезімталдық аймағын енгізуге болады. 1-суретте көрсетілгендей бейсызықты элементтің параметрлерін өзгерту үшін тілқатысу терезесін шақыруға болады.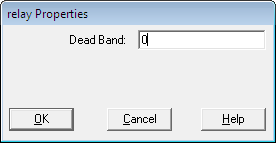



Сурет. 1. Релелік элементтің тілқатысу терезесі
Төмендегі сұлбада көрсетілген АБЖ құрастырып, сондай-ақ элементтерді тізбектей және параллель қосу арқылы АБЖ жұмысын тексереміз. Ол үшін 2-суретте көрсетілген сызбаны жинаймыз.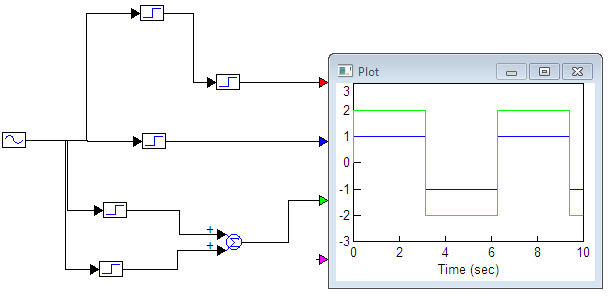



Сурет. 2. Бейсызықты элементтердің бірлік, параллель және тізбектей қосылуы
Жүйенің кірісіне sinusoid командасы бойынша Signal Producers бөлімінен синусоидалы сигнал беріледі. 2-суретте көрсетілгендей, кестедегі тізбекті және бірлік қосылған элементтер арасында еш айырмашылығы жоқ, өйткені элементтерді тізбектей қосу олардың жұмысына сәйкес келеді, ал параллельді қосу олардың қосындысына сәйкес келеді, сондықтан кестеде олардың сипаттамасы екі есе артты.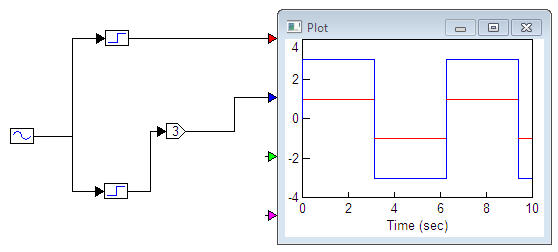


Сурет.3. Екі релелік сипаттамаларды салыстыру
Екінші жағынан, егер релелік элемент сигнум-функциямен іске асырылатыны белгілі болса, екі идеалды релелік элементті салыстыруға болады, онда біреуі gain буынының көмегімен үлкейтіледі. Ол үшін 3-суреттегі сұлбаны жинау қажет.

Осыдан кейін 4-суретте көрсетілгендей сезімтал емес элементтің сипаттамаларын де зерттейміз.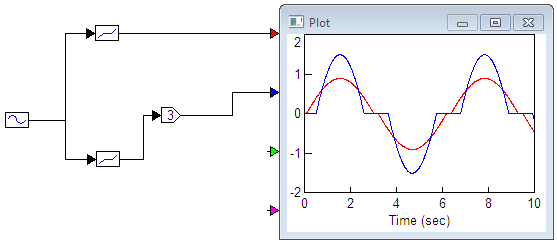



Сурет.4. Сезімталсыздық буын сипаттамалары
Limit буынын енгізу арқылы қанығу буынының сипаттамасын зерттейміз. Бұл 5-суретте ұсынылғандай етіп құрастырамыз.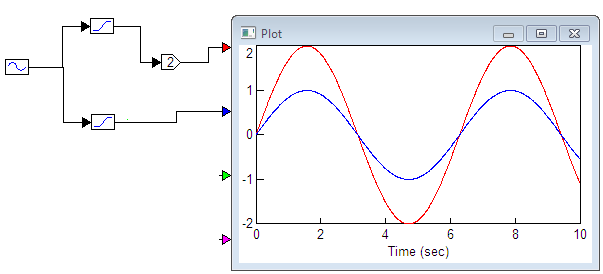


Сурет. 5. Екі қанығу сипаттамаларын салыстыру
Өзіндік жұмысқа арналған тапсырмалар

Студенттерге өзінің нұсқасына сәйкес сұлбаларды жинау, бейсызықты элементтердің параметрлерін өзгерту және олардың сипаттамаға әсерін бағалау қажет.

Кестеге сәйкес нұсқа бойынша сұлбаны құрастырып, АЖБ параметрлерін өзгерту арқылы оның қасиеттерін зерттеу қажет.

Нұсқа АБЖ параметрлері

Күшейту коэффициенті Сезімталсыздық Қанығу

1 2 0,6 20

2 3 0,4 20

3 4 0,4 30

4 2,5 0,3 30

5 2,3 0,2 20

6 3,5 0,6 20

7 3,2 0,5 34

8 3,4 0,6 50

9 4 0,4 50

10 4,3 0,2 60

11 2,5 0,6 100

12 2,6 0,5 50

13 2,7 0,8 50

14 3 0,1 60

15 3,1 0,6 30

16 2,5 2 30

17 2 2,1 20

18 1,5 2,0 30

19 1,8 2,3 60

20 1,6 2,4 55

21 2,3 1,8 50

22 2,2 1,6 40

23 2,6 1,9 85

24 2,5 1,4 50

25 2,8 1,5 60

26 3 0,8 20
Бақылау сұрақтары:

1. Бейсызықты автоматты реттеу жүйесі дегеніміз не?

2. Автономды бейсызықты АБЖ дегеніміз не?

3. АБЖ типтік бейсызықты элементтерін атаңыз.

4. Осы жұмыстағы әрбір бейсызықты элемент үшін аналитикалық өрнектерді жазыңыз.

5. АБЖ құрамына оларды қосқанда не болады?
2-ТАҚЫРЫП. Фазалық жазықтық туралы негізгі мәліметтер. Ерекше нүктелер мен ерекше сызықтар
Практикалық сабақ жоспары:

1. Сабақтың басында көрсетілген мысалды талқылау.

2. Көрсетліген мысалдардағы әдістерді бекіту мақсатында берілген есептерді шығару.

3. Шығарылған есептердің шешімін талқылау.

4. Практикалық жұмыс бойынша есепті рәсімдеу және оларды оқытушыға тексеруге тапсыру.
Тапсырмалар:

Мысал 1. Төмендегі сызықты жүйенің фазалық портретін құрастырыңыз.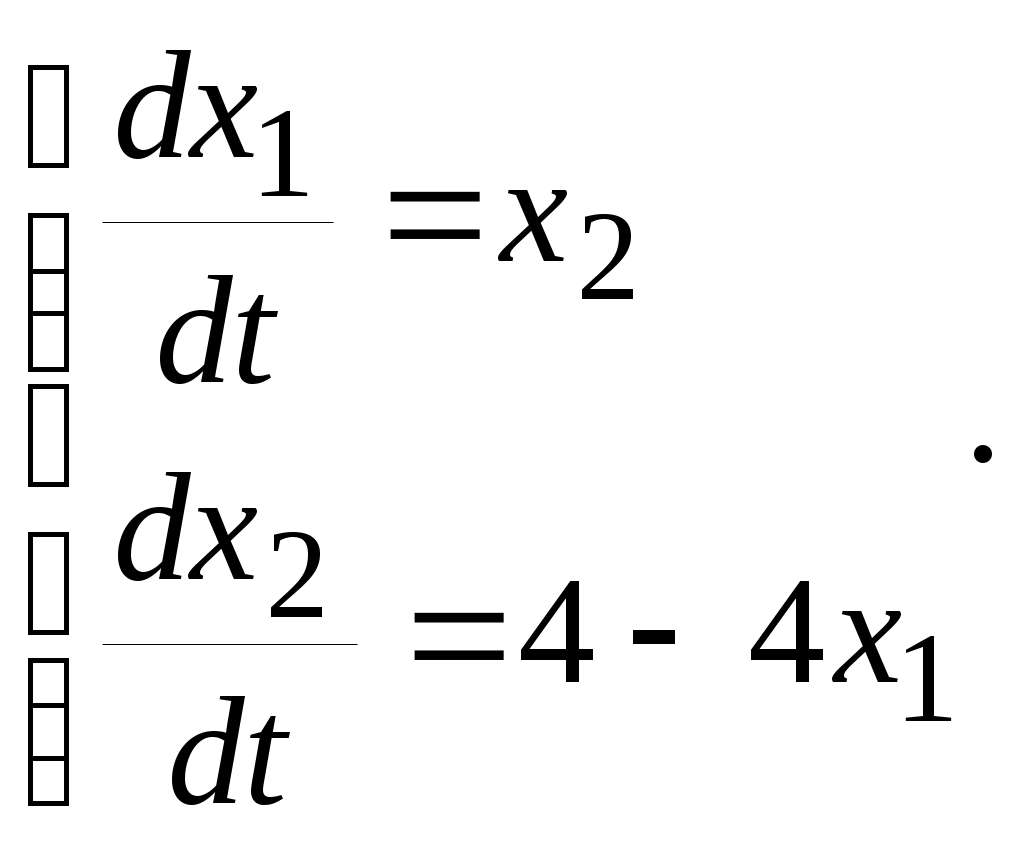



Есептің шешімі.




Фазалық траекториялар орталығы ығысқан шеңберлер. Фазалық траекториялар 1-суретте көрсетілген.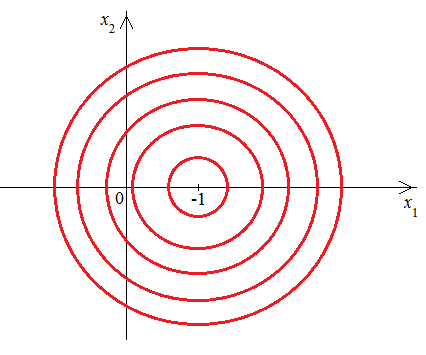



Сурет 1. Фазалық траекториялар

Өзіндік жұмысқа арналған тапсырмалар:

Есеп 1. Төмендегі сызықты жүйенің фазалық портретін құрастырыңыз.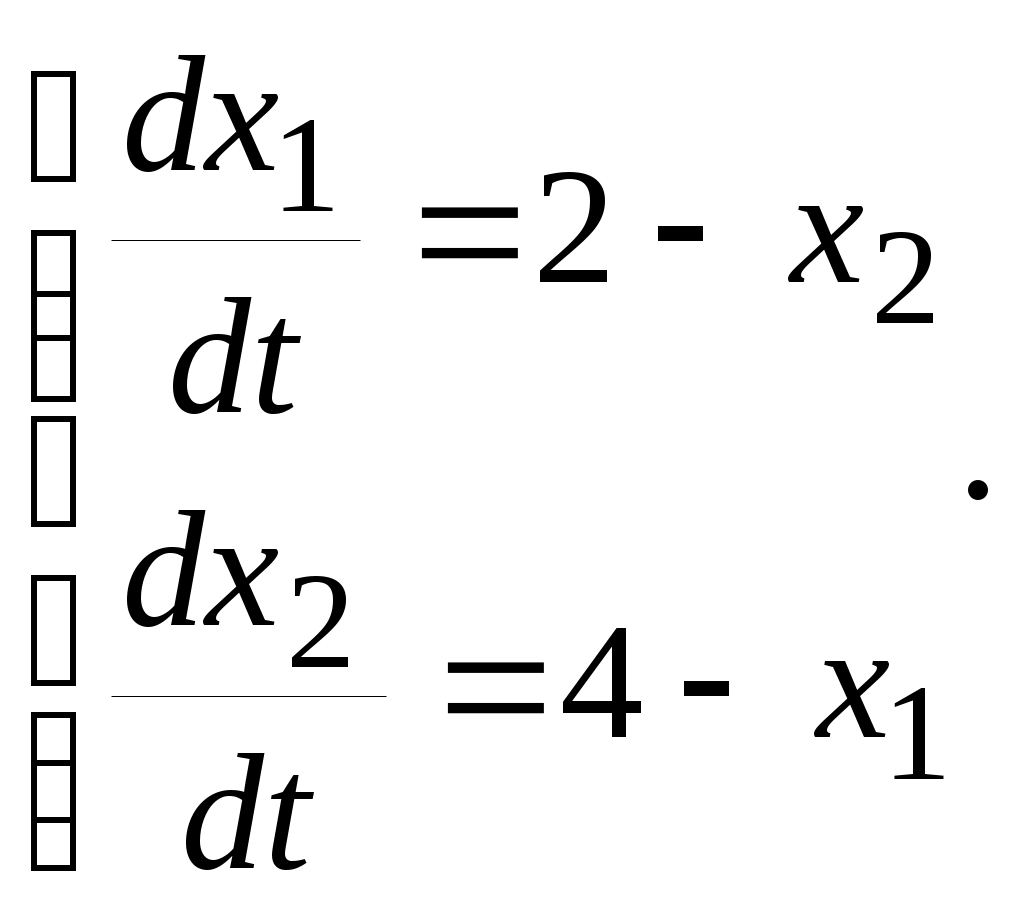


Есеп 2. Төмендегі сызықты жүйенің фазалық портретін құрастырыңыз.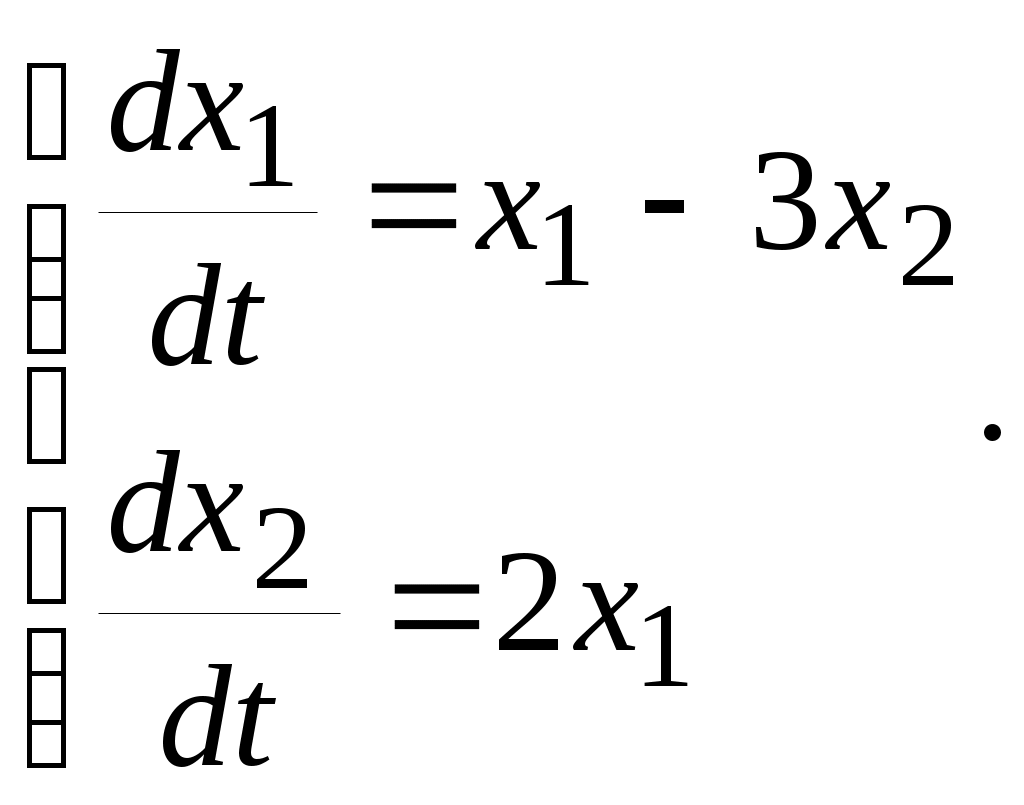


Есеп 3. Төмендегі сызықты жүйенің фазалық портретін құрастырыңыз.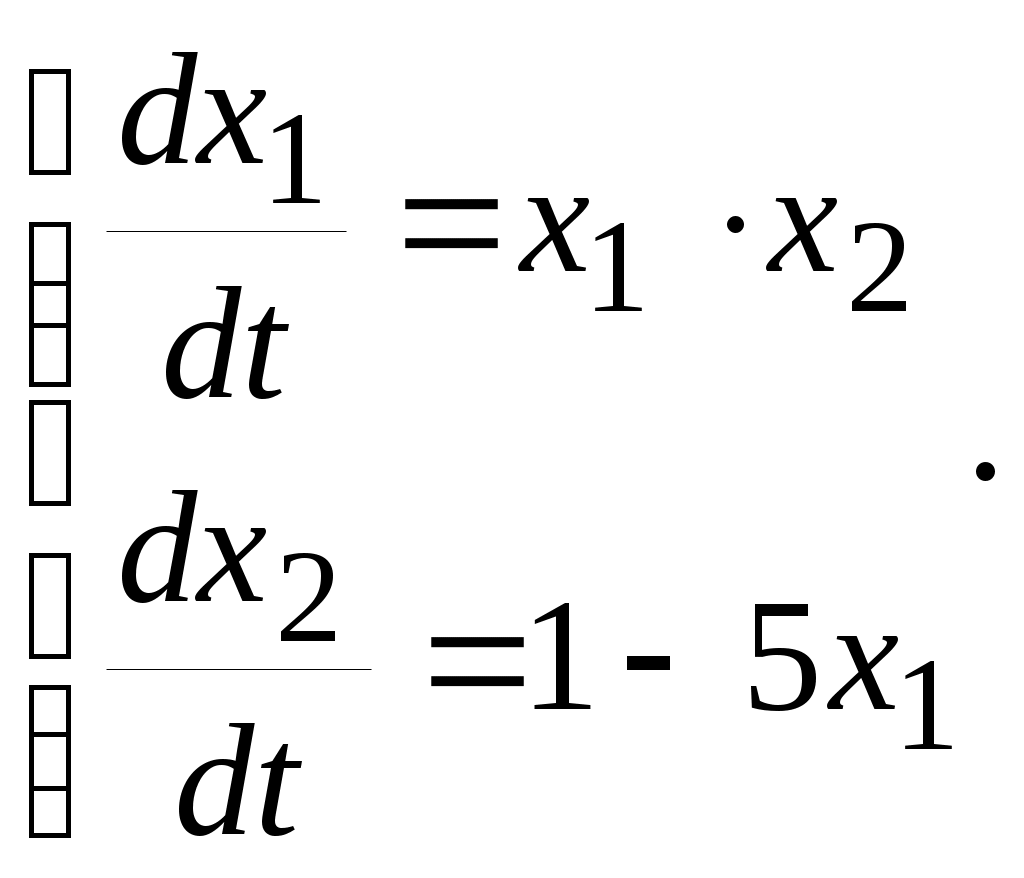


Есеп 4. Төмендегі сызықты жүйенің фазалық портретін құрастырыңыз.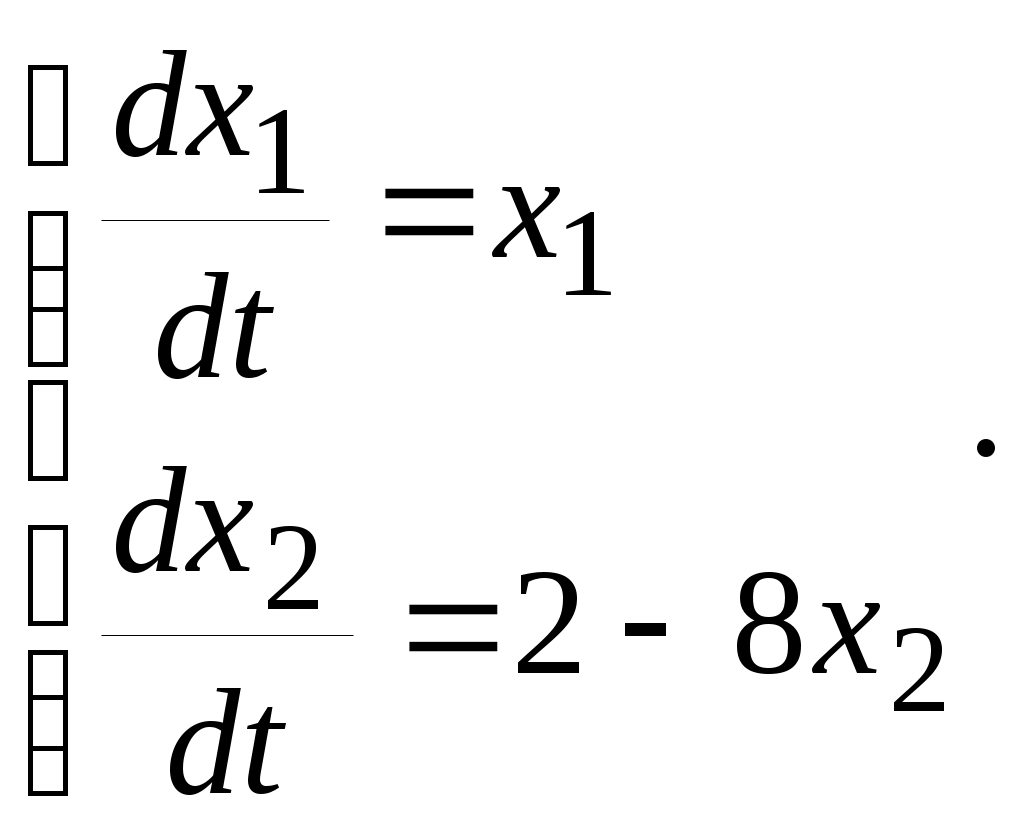


Бақылау сұрақтары:

1. Бейнелейтін нүкте дегеніміз не?

2. Жүйенің фазалық портреті дегеніміз не?

3. Жүйенің фазалық траекториясы дегеніміз не?

4. «Фазалық жазықтық» әдісінің кемшілігі неде?

5. Фазалық жазықтықта жүйенің қандай қозғалыстары оңай іске асырылады?
3-ТАҚЫРЫП. Фазалық жазықтықта ерекше нүктелерді зерттеу
Практикалық сабақ жоспары:

1. Сабақтың басында көрсетілген мысалды талқылау.

2. Көрсетліген мысалдардағы әдістерді бекіту мақсатында берілген есептерді шығару.

3. Шығарылған есептердің шешімін талқылау.

4. Практикалық жұмыс бойынша есепті рәсімдеу және оларды оқытушыға тексеруге тапсыру.
Тапсырмалар:

Мысал 1. Егер бейсызықты АРЖ құрамында төмендегідей сызықты бөлігі болса, оның фазалық жазықтық бетіндегі ерекше нүктелерін анықтаңыз:



Есептің шешімі. Есепті шешудің екі жолы бар. Бірінші жолы сызықты теңдеу түріндегі модельді теңдеулер жүйесі түріне келтіру қажет:

Соңғы теңдеудің кері Лаплас түрлендіруі арқылы түпнұсқасына келтіреміз: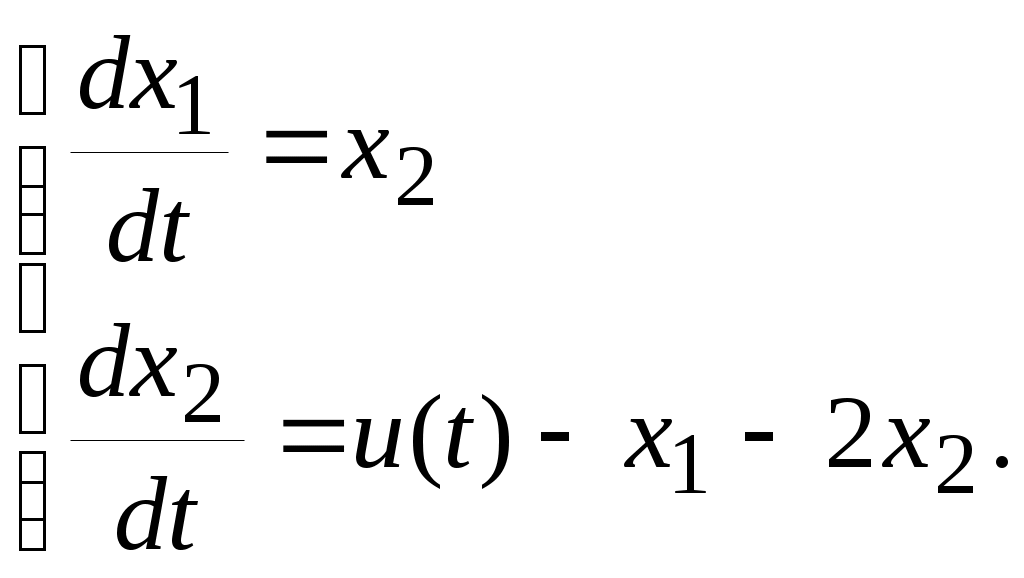


Соңғы теңдеулер жүйесінен ерекше нүктеледі алуға болатын, сипаттауыш теңдеуді құрастырамыз: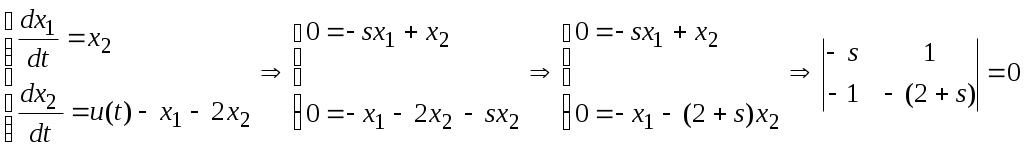

Соңғы анықтауыштан сипаттауышты табуға болады:

Соңғы сипаттауыш теңдеу беріліс функцияның бөлімі болып табылады. Сондықтан ерекше нүктелерді анықтаудың екінші жолы, беріліс функцияның бөлімін қарастыру. Енді осы теңдеудің түбірлерін анықтау қажет:

Түбірлер комплексті-түйіндес болып шықты, яғни ерекше нүктелер орнықты фокус болып табылады.


Өзіндік жұмысқа арналған тапсырмалар:

Есеп 1. Егер бейсызықты АРЖ құрамында төмендегідей сызықты бөлігі болса, оның фазалық жазықтық бетіндегі ерекше нүктелерін анықтаңыз:


Есеп 2. Егер бейсызықты АРЖ құрамында төмендегідей сызықты бөлігі болса, оның фазалық жазықтық бетіндегі ерекше нүктелерін анықтаңыз:



Есеп 3. Егер бейсызықты АРЖ құрамында төмендегідей сызықты бөлігі болса, оның фазалық жазықтық бетіндегі ерекше нүктелерін анықтаңыз:



Есеп 4. Егер бейсызықты АРЖ құрамында төмендегідей сызықты бөлігі болса, оның фазалық жазықтық бетіндегі ерекше нүктелерін анықтаңыз:



Есеп 5. Егер бейсызықты АРЖ құрамында төмендегідей сызықты бөлігі болса, оның фазалық жазықтық бетіндегі ерекше нүктелерін анықтаңыз:



Бақылау сұрақтары:

1. Жүйенің фазалық портреті дегеніміз не?

2. Түйін түрлі ерекше нүктесі дегеніміз не? Ол қашан орын алады?

3. Ер-тұрман түрлі ерекше нүктесі дегеніміз не? Ол қашан орын алады?

4. Шекті цикл дегеніміз не?

5. Орталық нүктесі дегеніміз не? Ол қашан орын алады?

6. Фокус ерекше нүктесі дегеніміз не? Ол қашан орын алады?

7. Ер-тұрманның орнықты нүктесі бар ма? Неге түсіндіріңіз.
4-ТАҚЫРЫП. Орнықтылық туралы ілімді анықтау. Жүйелердің «кіші», «үлкен» және «тұтас» орнықтылығы. Абсолюттік орнықтылық туралы негізгі ұғым.
Практикалық сабақ жоспары:

1. Сабақтың басында көрсетілген мысалды талқылау.

2. Көрсетліген мысалдардағы әдістерді бекіту мақсатында берілген есептерді шығару.

3. Шығарылған есептердің шешімін талқылау.

4. Практикалық жұмыс бойынша есепті рәсімдеу және оларды оқытушыға тексеруге тапсыру.
Тапсырмалар:

Есеп 1. Келесі теңдеулер жүйесі арқылы берілген автоматты реттеу жүйесі үшін Ляпунов функциясын құрастыру қажет: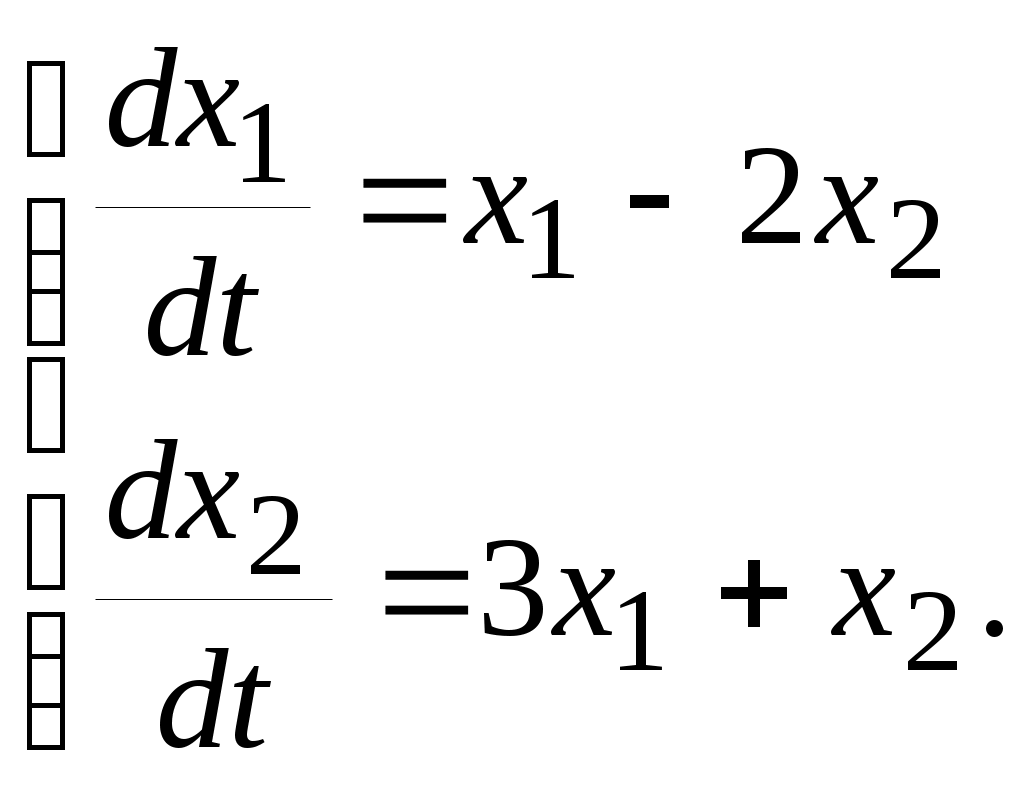



Есептің шешімі. Ляпунов функциясын табудың әмбебап алгоритмы мен толық тәсілі жоқ, сондықтан Ляпунов функцияларын табудың кейбір жағдайларда қолданылатын амалдары болады.

Солардың бірі Ляпунов функциясын келесі түрде қарастыру:



Бұл тәсілдің ерекшелігі Ляпунов функциясы араласпаған екі бөлік айнымалыдан тұратын функцияның қосындысы ретінде қарастыру.

Ляпунов функциясының туындысын қарастырамыз:





Алдыңғы тұжырымға сәйкес Ляпунов функциясының араласқан айнымалылары бар мүшелері болмауы тиіс, сондықтан бірден екі айнымалысы бар мүшелер нольге теңболуы тиіс:



Енді соңғы пайда болған дифференциал теңдеуден белгісіз функцияларды интегралдау арқылы табамыз. Ол үшін бірдей айнымалыларды теңдіктің бір бөлігіне топтаймыз: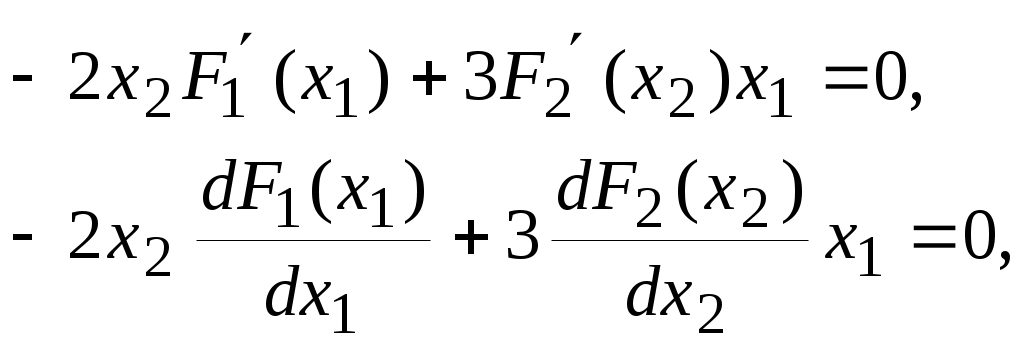





Соңғы теңдікті бірдей тұрақты санға теңестіріп, белгісіз функцияларды табамыз:







Енді Ляпунов функциясы келесідей болады:



Өзіндік жұмысқа арналған тапсырмалар:

Есеп 1. Келесі теңдеулер жүйесі арқылы берілген автоматты реттеу жүйесі үшін Ляпунов функциясын құрастыру қажет: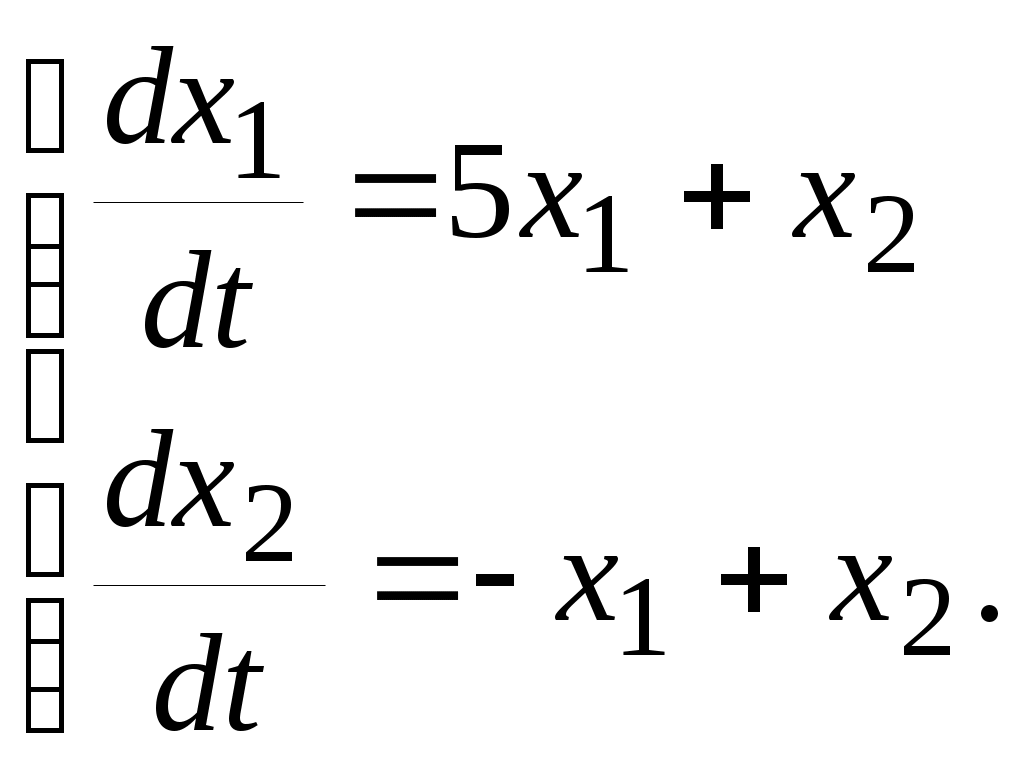


Есеп 2. Келесі теңдеулер жүйесі арқылы берілген автоматты реттеу жүйесі үшін Ляпунов функциясын құрастыру қажет: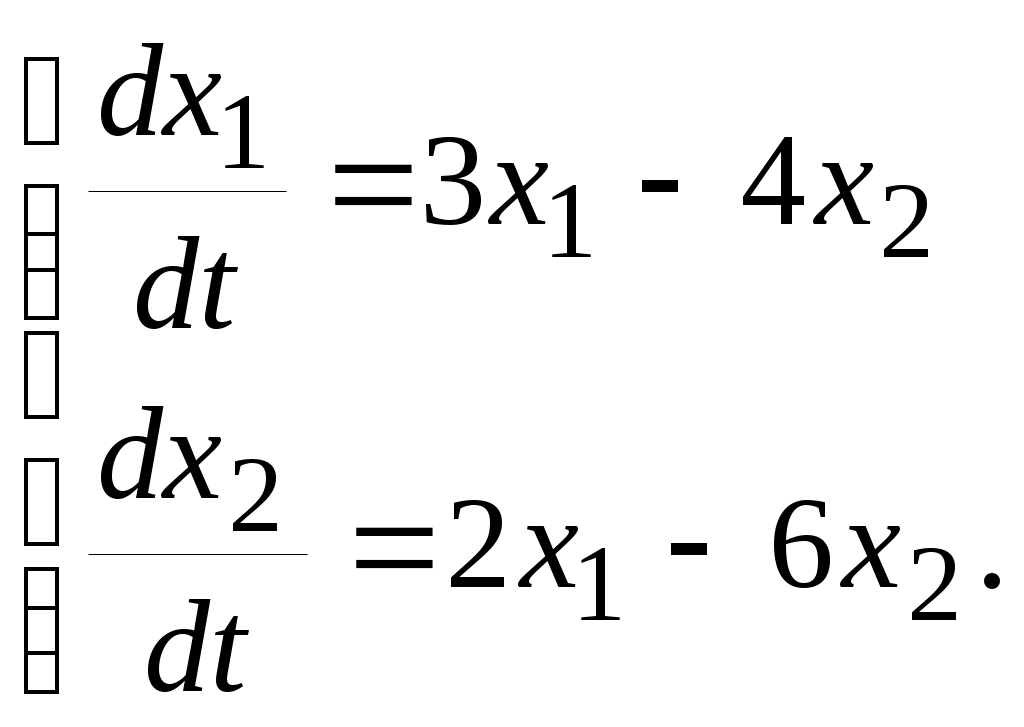


Есеп 3. Келесі теңдеулер жүйесі арқылы берілген автоматты реттеу жүйесі үшін Ляпунов функциясын құрастыру қажет: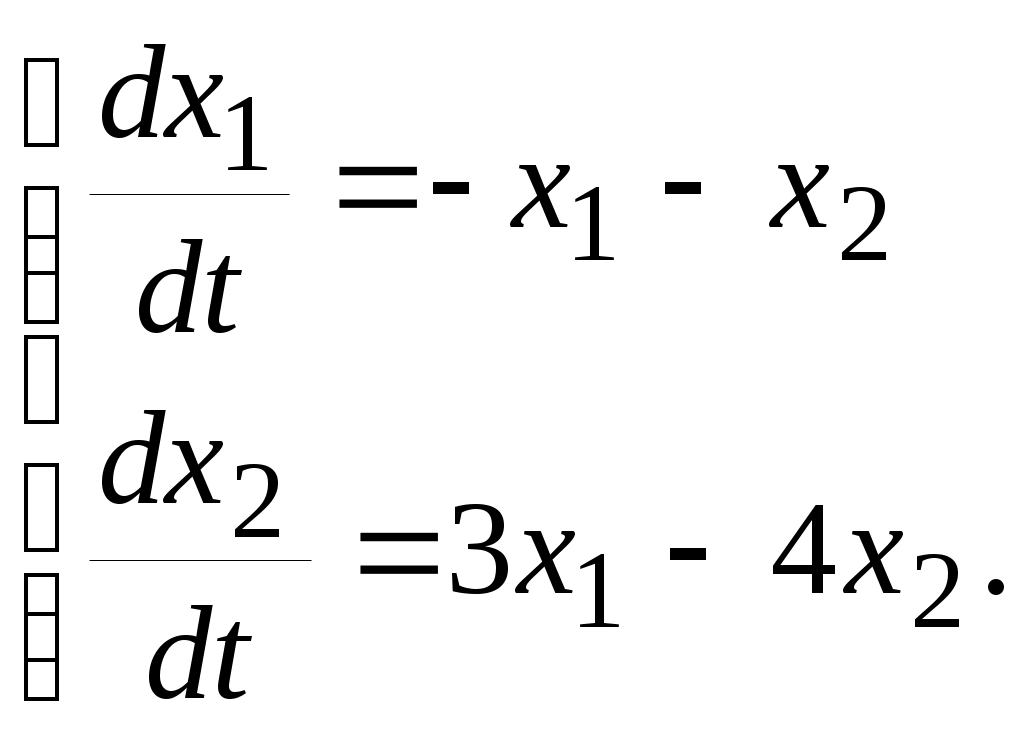



Есеп 4. Келесі теңдеулер жүйесі арқылы берілген автоматты реттеу жүйесі үшін Ляпунов функциясын құрастыру қажет: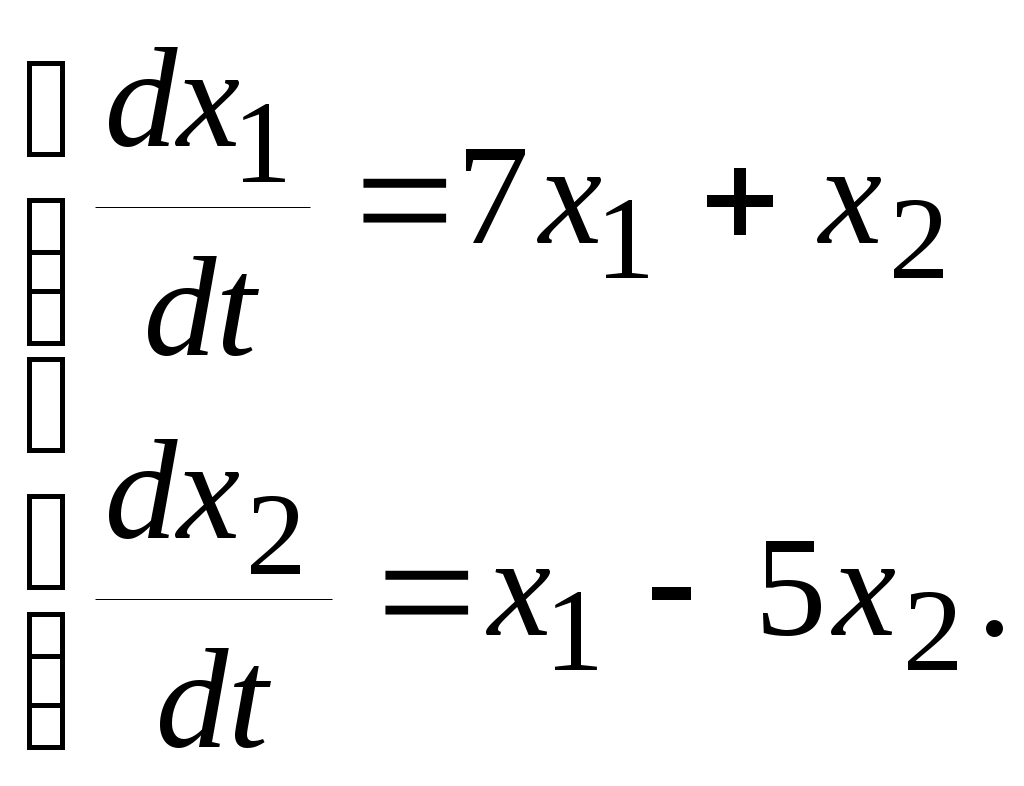


Есеп 5. Келесі теңдеулер жүйесі арқылы берілген автоматты реттеу жүйесі үшін Ляпунов функциясын құрастыру қажет: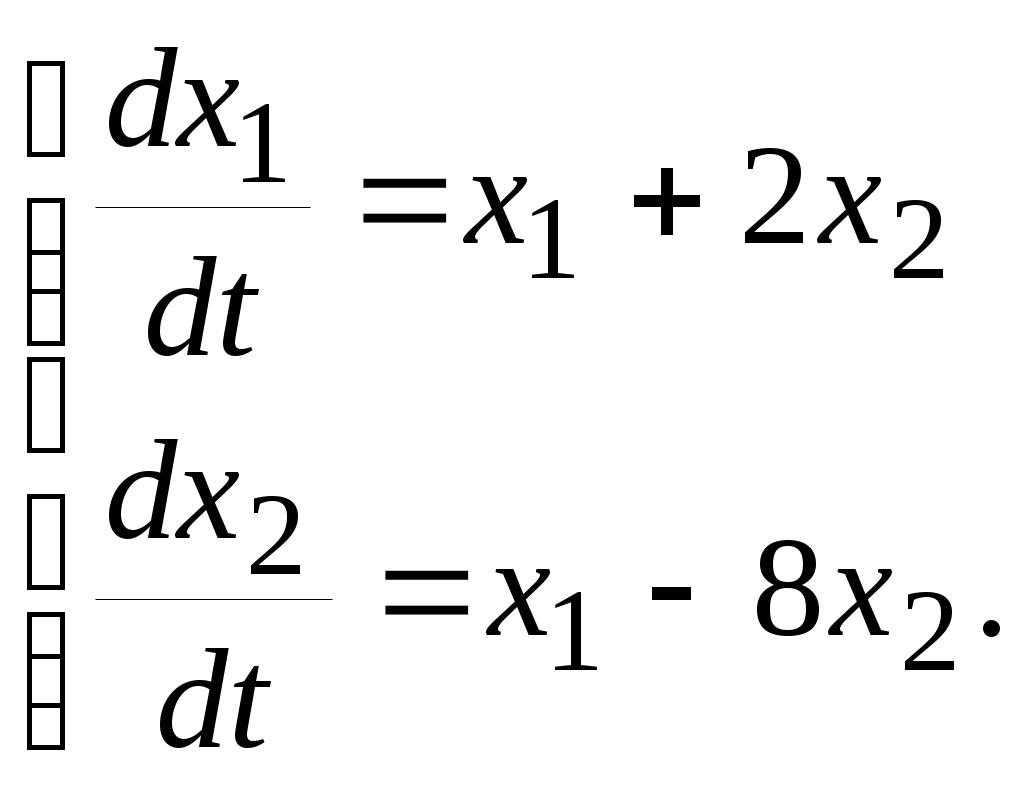


Бақылау сұрақтары:

1. Орнықтылық дегеніміз не? Оның қандай түрлері болады?

2. «Кіші» орнықтылық дегеніміз не?

3. «Үлкен» орнықтылық дегеніміз не?

4. «Тұтас» орнықтылық деген не?

5. Абсолюттік орнықтылық деген не?
5-ТАҚЫРЫП. В.М. Поповтың абсолюттік орнықтылық туралы теоремасы. В.М. Поповтың теоремасы шарттарының графикалық түсіндірмесі
Практикалық сабақ жоспары:

1. Сабақтың басында көрсетілген мысалды талқылау.

2. Көрсетліген мысалдардағы әдістерді бекіту мақсатында берілген есептерді шығару.

3. Шығарылған есептердің шешімін талқылау.

4. Практикалық жұмыс бойынша есепті рәсімдеу және оларды оқытушыға тексеруге тапсыру.
Тапсырмалар:
Есеп 1. Егер автоматты басқару жүйесінің сұлбасы суреттегідей болса, оның абсолюттік орнықтылығын Попов теоремасы арқылы тексеріңіз. Жүйенің бейсызықты сипаттамасының параметрлері мен сызықты бөлігінің беріліс функциясы келесідей: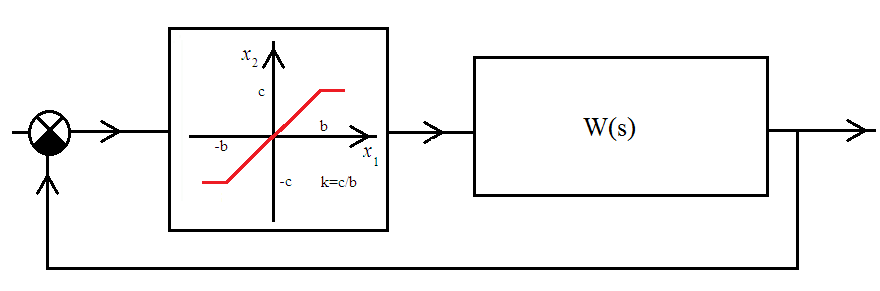





Есептің шешімі. Бейсызықты сипаттаманы коэффициенті арқылы шектеуге болады.

АБЖ сипаттауыш теңдеуі келесі формуламен беріліс функцияның бөлімі арқылы жазылады:



Содан кейін АБЖ жиіліктік береліс функциясының формуласын дайындаймыз: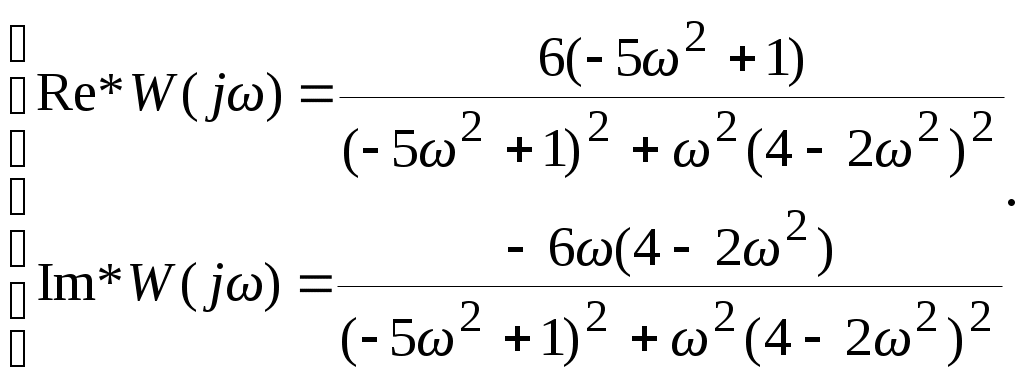

	0	1/√5	√2	∞
	6	0	-0,67	0
	0	-3,73	0	0

Енді комплекстік жазықтық бетіне осы годографты және критикалық нүктенің 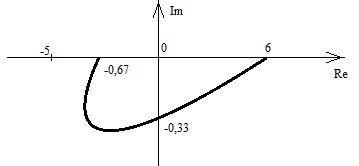мәнін түсіреміз. Осы кртикалық нүкте арқылы бірнеше түзу сызықтар өткізуге болады және годографтың графигі осы сызықтарды қиып өтпей де сол жағынан орналасады.


Годограф пен критикалық нүкте орналасуы
Жауабы: Берілген АБЖ абсолюттік орнықты болып табылады.
Өзіндік жұмысқа арналған тапсырмалар:
Есеп 1. Егер автоматты басқару жүйесінің сұлбасы суреттегідей болса, оның абсолюттік орнықтылығын Попов теоремасы арқылы тексеріңіз. Жүйенің бейсызықты сипаттамасының параметрлері мен сызықты бөлігінің беріліс функциясы келесідей: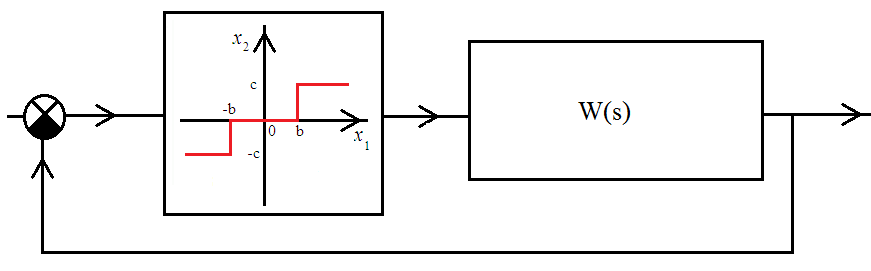



Есеп 2. Егер автоматты басқару жүйесінің сұлбасы суреттегідей болса, оның абсолюттік орнықтылығын Попов теоремасы арқылы тексеріңіз. Жүйенің бейсызықты сипаттамасының параметрлері мен сызықты бөлігінің беріліс функциясы келесідей: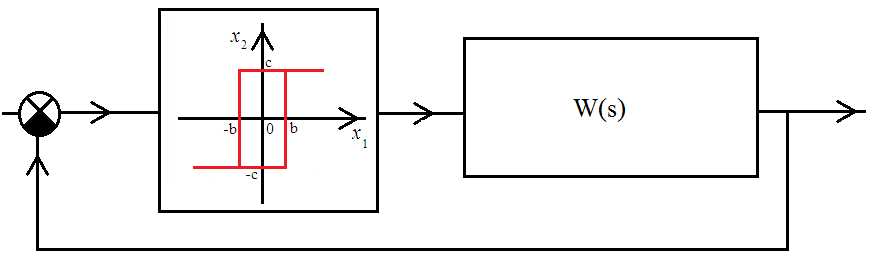



Есеп 3. Егер автоматты басқару жүйесінің сұлбасы суреттегідей болса, оның абсолюттік орнықтылығын Попов теоремасы арқылы тексеріңіз. Жүйенің бейсызықты сипаттамасының параметрлері мен сызықты бөлігінің беріліс функциясы келесідей: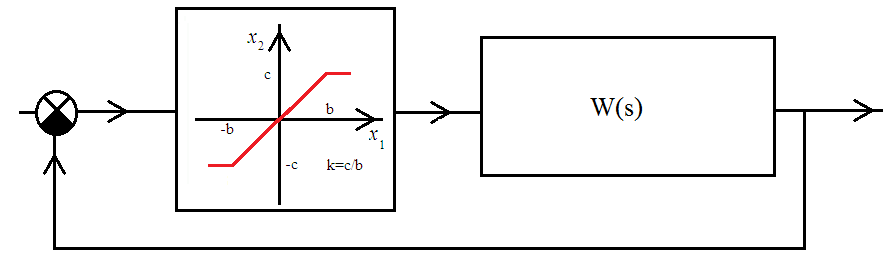



Бақылау сұрақтары:

1. Попов теоремасының мәні неде?

2. Попов теоремасын АРЖ орнықтылығын зерттеу үшін қалай қолданады?

3. Жүйенің абсолюттік тұрғыдан орнықты болу үшін, оның сызықты бөлігі маңызды ма?
6-ТАҚЫРЫП. А.М. Ляпуновтың екінші әдісі туралы негізгі мәліметтер. Ляпуновтың екінші әдісінің теоремалары

Практикалық сабақ жоспары:

1. Сабақтың басында көрсетілген мысалды талқылау.

2. Көрсетліген мысалдардағы әдістерді бекіту мақсатында берілген есептерді шығару.

3. Шығарылған есептердің шешімін талқылау.

4. Практикалық жұмыс бойынша есепті рәсімдеу және оларды оқытушыға тексеруге тапсыру.
Тапсырмалар:

Есеп 1. Келесі теңдеулер жүйесі арқылы берілген автоматты реттеу жүйесінің орнықтылығын Ляпуновтың екінші әдісі арқылы тексеріңіз: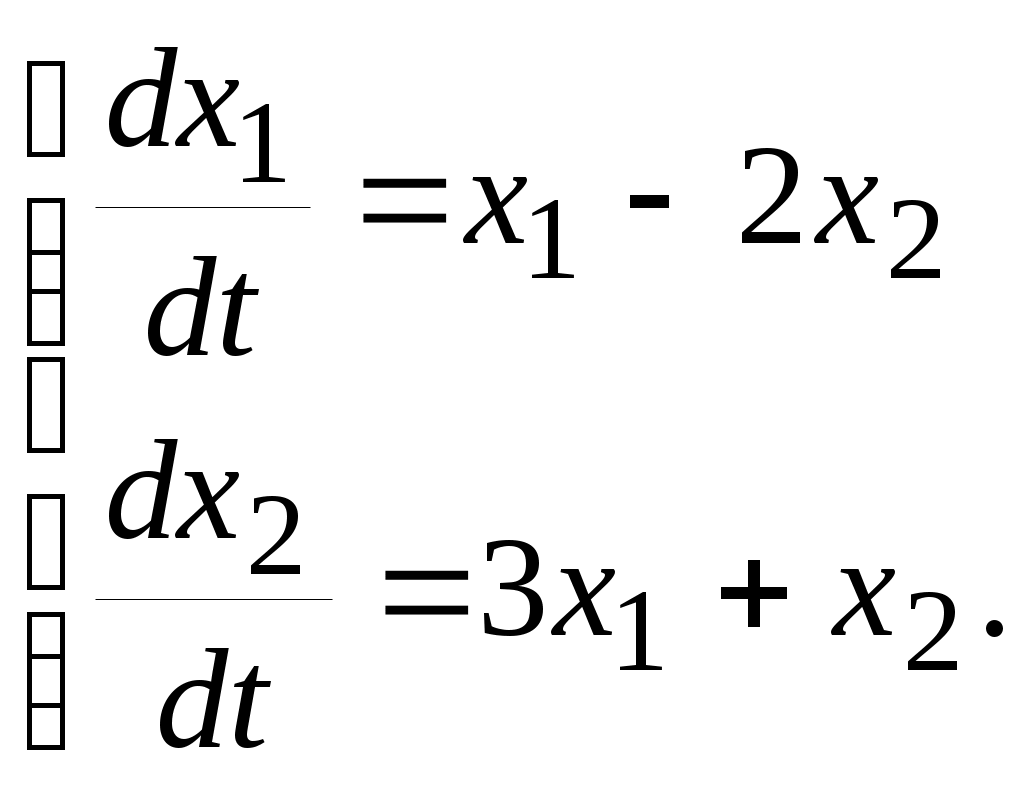



Есептің шешімі. Ляпунов функциясын табу қажет. Ляпунов функциясын келесі түрде қарастырып көреміз:



Ляпунов функциясының туындысын қарастырамыз:







Мұндағы коэффициенттерді табу оңай емес, сондықтан Ляпунов функциясы квадраттық форма болсын деп, коэффициенттерін тағайындайық та, соңғы коэффициентті табайық:



Осыған сәйкес Ляпунов:



Ляпунов функциясы оң мәнді функция болып шықты.

Енді Ляпуновтың екінші әдісіне сәйкес, Ляпунов функциясының туындысын тауып аламыз:


Ляпунов функциясы туындысының таңбасы өзгерген жоқ, сондықтан автоматты реттеу жүйесі орнықсыз болып табылады.
Өзіндік жұмысқа арналған тапсырмалар:
Есеп 1. Келесі теңдеулер жүйесі арқылы берілген автоматты реттеу жүйесінің орнықтылығын Ляпуновтың екінші әдісі арқылы тексеріңіз: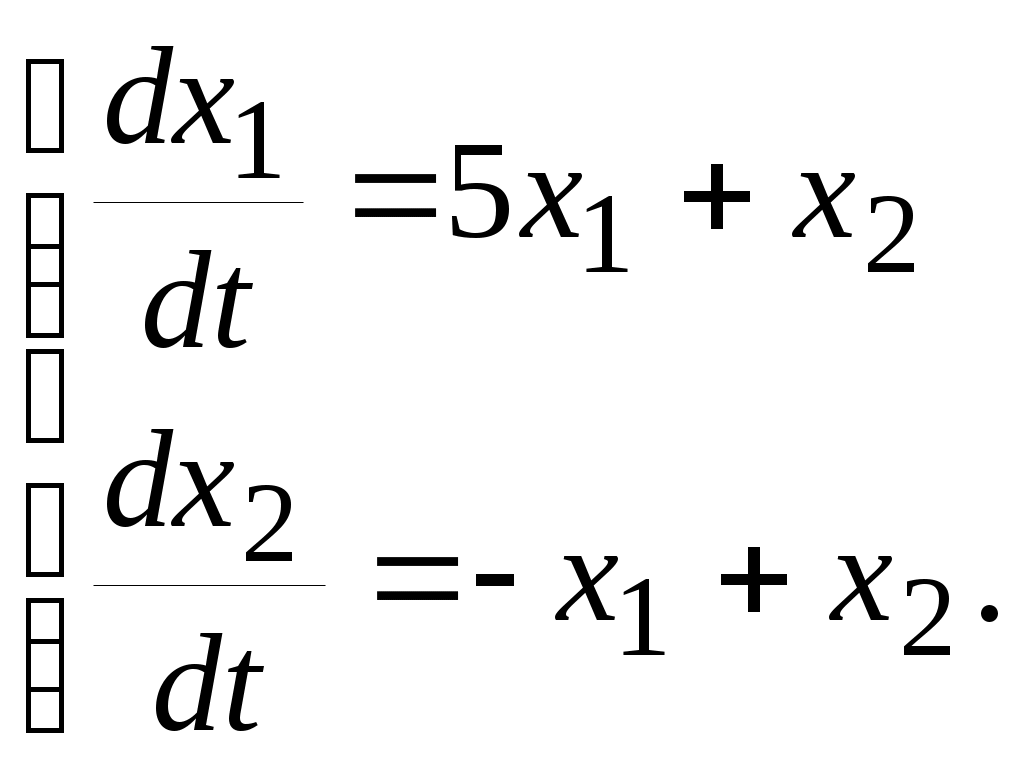


Есеп 2. Келесі теңдеулер жүйесі арқылы берілген автоматты реттеу жүйесінің орнықтылығын Ляпуновтың екінші әдісі арқылы тексеріңіз: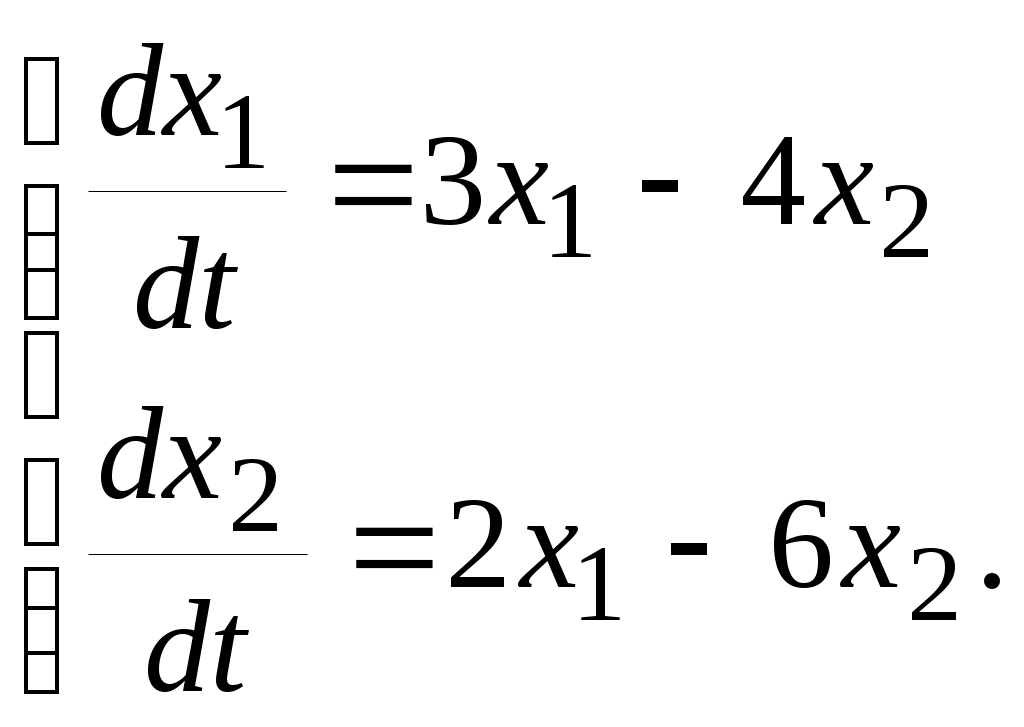


Есеп 3. Келесі теңдеулер жүйесі арқылы берілген автоматты реттеу жүйесінің орнықтылығын Ляпуновтың екінші әдісі арқылы тексеріңіз: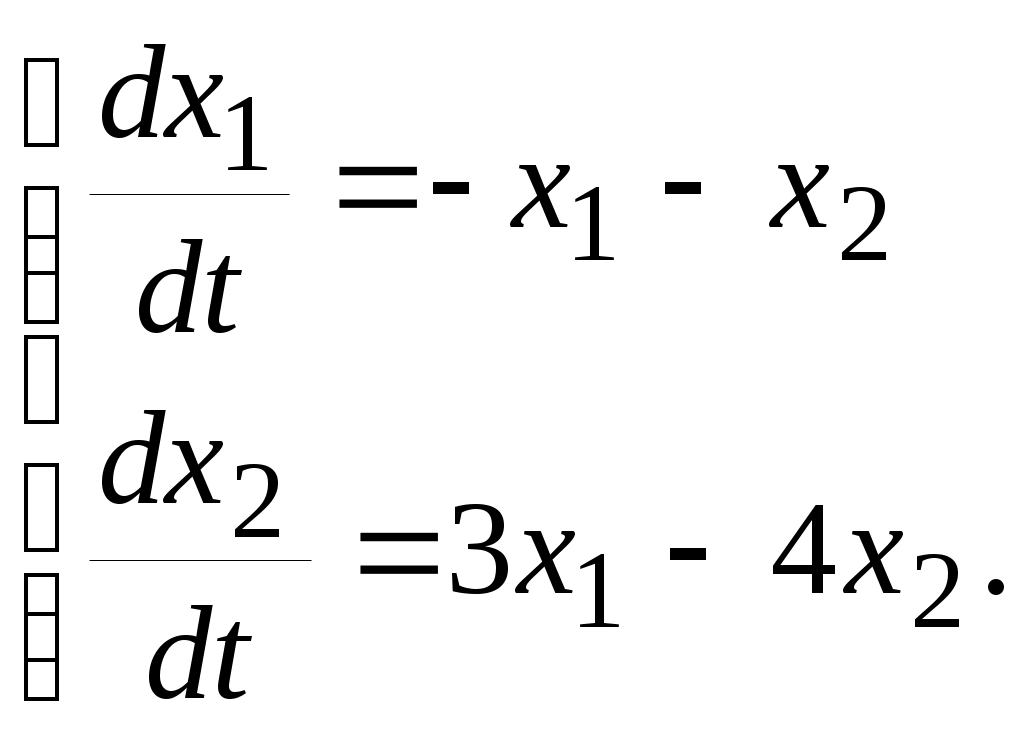



Есеп 4. Келесі теңдеулер жүйесі арқылы берілген автоматты реттеу жүйесінің орнықтылығын Ляпуновтың екінші әдісі арқылы тексеріңіз: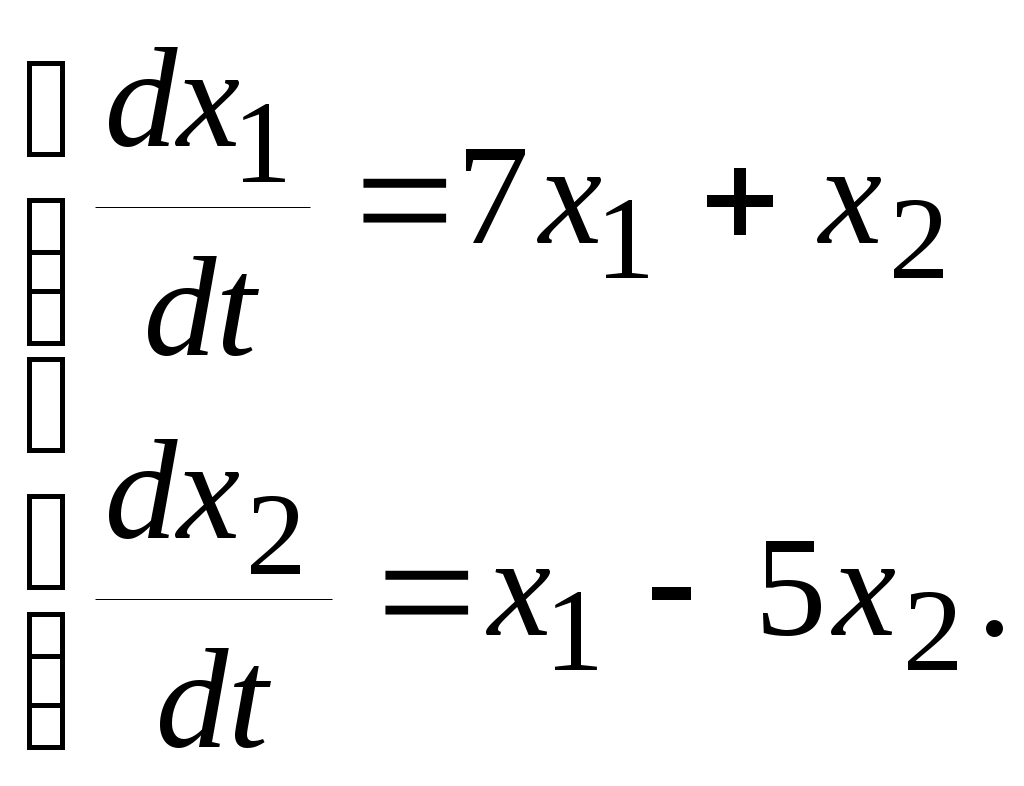


Есеп 5. Келесі теңдеулер жүйесі арқылы берілген автоматты реттеу жүйесінің орнықтылығын Ляпуновтың екінші әдісі арқылы тексеріңіз: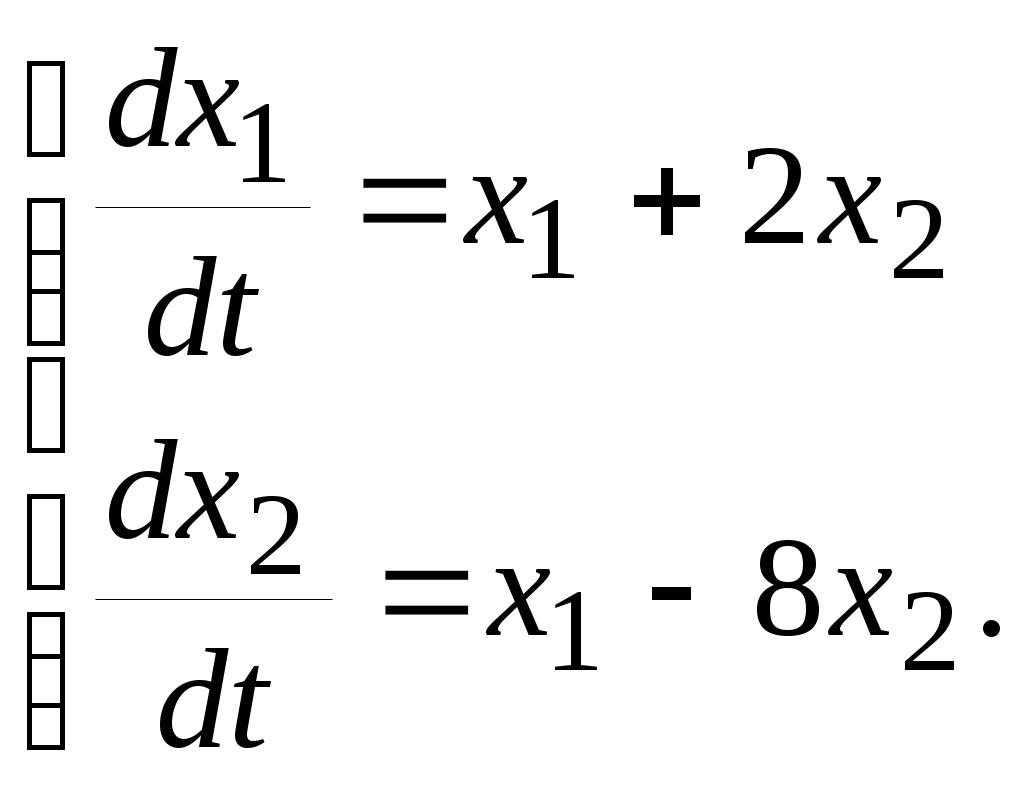


Бақылау сұрақтары:

1. Ляпунов функциялараның түрлері қандай болуы мүмкін?

2. Ляпуновтың бірінші әдісінің мәні неде?

3. Ляпуновтың екінші әдісінің мәні неде? Оны түсіндіріп беріңіз.

4. Ляпунов функцияларын қалай табады?

5. Ляпуновтың орнықтылық теоремаларын айтып беріңіз.
7-ТАҚЫРЫП. Гармоникалық баланс әдісі. Гармоникалық сызықтандыру және оның коэффициенттері
Практикалық сабақ жоспары:

1. Сабақтың басында көрсетілген мысалды талқылау.

2. Көрсетліген мысалдардағы әдістерді бекіту мақсатында берілген есептерді шығару.

3. Шығарылған есептердің шешімін талқылау.

4. Практикалық жұмыс бойынша есепті рәсімдеу және оларды оқытушыға тексеруге тапсыру.
Тапсырмалар:

Есеп 1. Егер бейсызықты автоматты басқару жүйесінде бейсызықты элемент төмендегі статикалық сипаттамасы арқылы берілсе, жүйенің гармоникалық сызықтандырылған беріліс функциясын табыңыз. Статикалық сипаттама параметрлері: 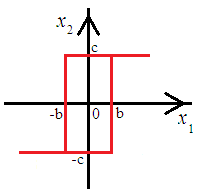және


Есептің шешімі. Біріншіден осы сипаттамаға сәйкес гармоникалық коэффициенттер келесідей болады, беріліс функциясы оңай табылады: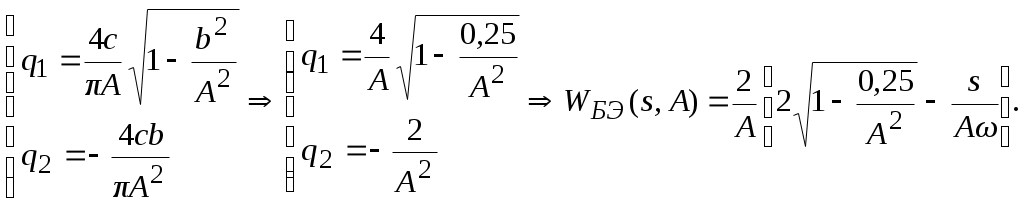


Өзіндік жұмысқа арналған тапсырмалар:
Есеп 1. Егер бейсызықты автоматты басқару жүйесінде бейсызықты элемент төмендегі статикалық сипаттамасы арқылы берілсе, жүйенің гармоникалық сызықтандырылған беріліс функциясын табыңыз. Статикалық сипаттама параметрлері: 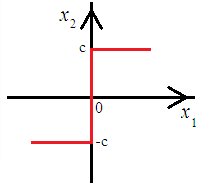және

Есеп 2. Егер бейсызықты автоматты басқару жүйесінде бейсызықты элемент төмендегі статикалық сипаттамасы арқылы берілсе, жүйенің гармоникалық сызықтандырылған беріліс функциясын табыңыз. Статикалық сипаттама параметрлері: 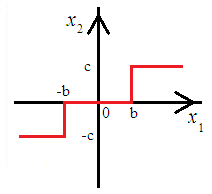және


Есеп 3. Егер бейсызықты автоматты басқару жүйесінде бейсызықты элемент төмендегі статикалық сипаттамасы арқылы берілсе, жүйенің гармоникалық сызықтандырылған беріліс функциясын табыңыз. Статикалық сипаттама параметрлері: 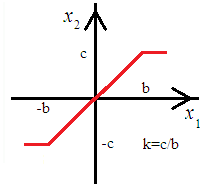және


Есеп 4. Егер бейсызықты автоматты басқару жүйесінде бейсызықты элемент төмендегі статикалық сипаттамасы арқылы берілсе, жүйенің гармоникалық сызықтандырылған беріліс функциясын табыңыз. Статикалық сипаттама параметрлері: 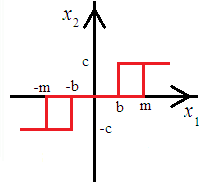және



Есеп 5. Егер бейсызықты автоматты басқару жүйесінде бейсызықты элемент төмендегі статикалық сипаттамасы арқылы берілсе, жүйенің гармоникалық сызықтандырылған беріліс функциясын табыңыз. Статикалық сипаттама параметрлері: 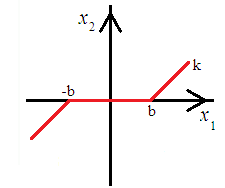және


Бақылау сұрақтары:

1. Гармоникалық баланс әдісі деген не?

2. Гармоникалық коэффициенттерді есептеудің алгоритмі қандай?

3. Гармоникалық сызықтандырудың негізгі ойы қандай?

4. Фильтр гипотезасы деген не?

5. Гармоникалық сызықтандыру шарттары қандай?
8-ТАҚЫРЫП. Л.С. Гольдфарб пен Д. Коченбургер әдістері арқылы бейсызықты АРЖ зерттеу
Практикалық сабақ жоспары:

1. Сабақтың басында көрсетілген мысалды талқылау.

2. Көрсетліген мысалдардағы әдістерді бекіту мақсатында берілген есептерді шығару.

3. Шығарылған есептердің шешімін талқылау.

4. Практикалық жұмыс бойынша есепті рәсімдеу және оларды оқытушыға тексеруге тапсыру.
Тапсырмалар:
Есеп 1. Автоматты басқару жүйесінің құрамында бейсызықты элемент статикалық сипаттамасымен берілген, осы жүйеде орнайтын автотербелістердің орнықты параметрлерін Л.С. Гольдфарб әдісі арқылы табу қажет.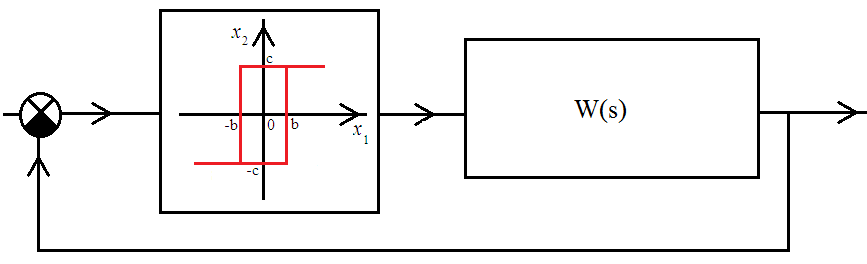



Есептің шешімі. Жүйенің гармоникалық коэффициенттерін табу қажет және оның сызықтандырылған беріліс функциясын анықтап, годографтарын комплекстік жазықтық бетіне түсіру қажет.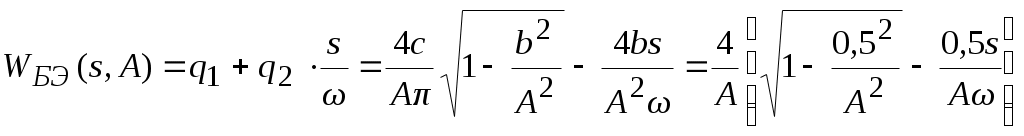



және
Сызықты бөліктің сипаттамасын құрастыру үшін:


Бейсызықты бөліктің сипаттамасын құрастыру үшін:

Екі сипаттаманың қиылысқан нүктелірін табу арқылы орнықты автотербелістер параметрлерін анықтаймыз: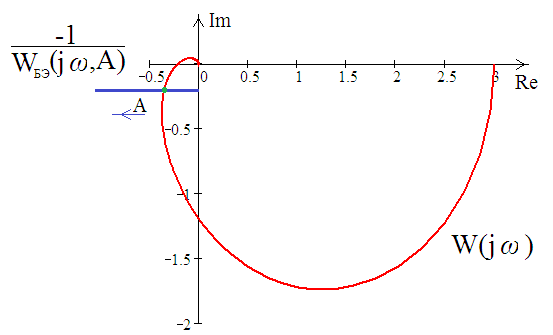



Автотербелістер параметрлерін анықтау
Жүйедегі автотербелістер апараметрлері:

1. және ;

2. және .
Өзіндік жұмысқа арналған тапсырмалар:

Есеп 1. Автоматты басқару жүйесінің құрамында бейсызықты элемент статикалық сипаттамасымен берілген, осы жүйеде орнайтын автотербелістердің орнықты параметрлерін Л.С. Гольдфарб әдісі арқылы табу қажет.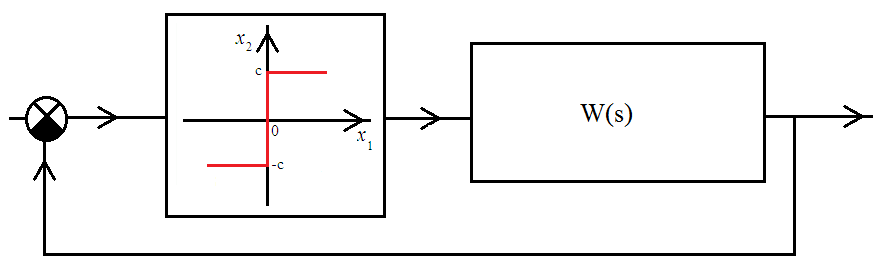




Есеп 2. Автоматты басқару жүйесінің құрамында бейсызықты элемент статикалық сипаттамасымен берілген, осы жүйеде орнайтын автотербелістердің орнықты параметрлерін Л.С. Гольдфарб әдісі арқылы табу қажет.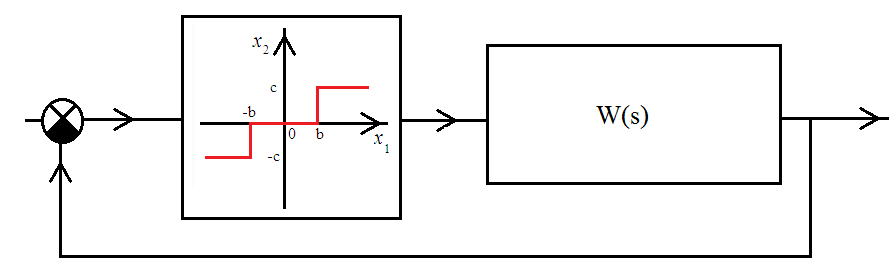




Есеп 3. Автоматты басқару жүйесінің құрамында бейсызықты элемент статикалық сипаттамасымен берілген, осы жүйеде орнайтын автотербелістердің орнықты параметрлерін Л.С. Гольдфарб әдісі арқылы табу қажет.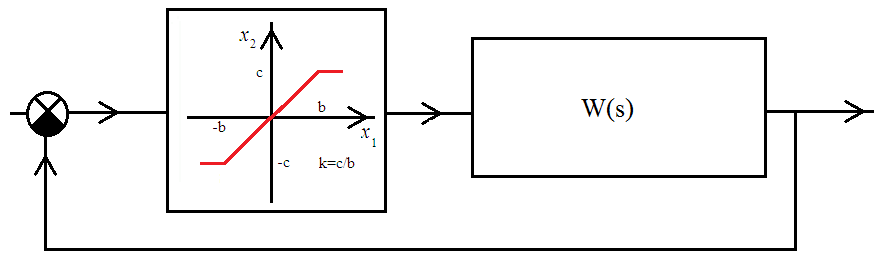



Бақылау сұрақтары:

1. Гармоникалық баланс әдісі деген не?

2. Гольдфарб әдісінің негізгі мәні неде?

3. Гармоникалық коэффициенттерді есептеудің алгоритмі қандай?

4. Коченбург әдісі Гольдфарб әдісінен немен ерекшеленеді?

5. Автотербеліс деген не?
9-ТАҚЫРЫП. Дискретті және импульсттік элементтері бар автоматты басқару жүйелері. Модуляция туралы негізгі ілім
Практикалық сабақ жоспары:

1. Сабақтың басында көрсетілген мысалды талқылау.

2. Көрсетліген мысалдардағы әдістерді бекіту мақсатында берілген есептерді шығару.

3. Шығарылған есептердің шешімін талқылау.

4. Практикалық жұмыс бойынша есепті рәсімдеу және оларды оқытушыға тексеруге тапсыру.
Тапсырмалар:

Есеп 1. Берілген үздіксіз сигналдың амплитудалық модуляциясы орындалғаннан кейінгі сигналдың графигін құрастыру. Модуляцияланған дискреттік сигналдың дискреттеу периоды 100 мс, ал бір импульстің ұзақтығы 50 мс. Сигнал:

Есептің шешімі. Амплитудалық модуляция жағдайында импульстердің ені тұрақты болады да, олардың амплитудасы өзгереді. Есепті шешу барысында осыны ескеру қажет.

Үздіксіз сигналдың графигін құрастырып, оның үстіне модуляцияланған дискреттік сигналдың графигін құрастырамыз.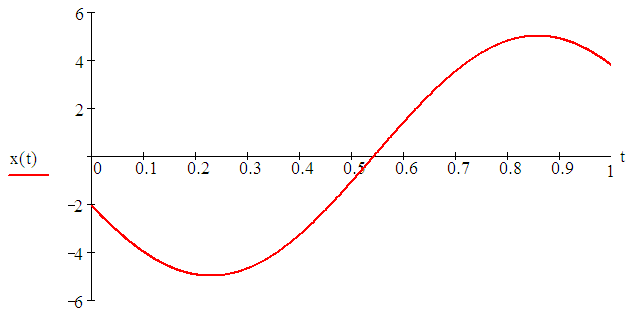


Үздіксіз сигнал графигі
Енді осы сигналды дискреттеу арқылы, амплитудалық модуляцияланған дискреттік сигналдың графигін құрастырамыз. Дискреттеу периоды 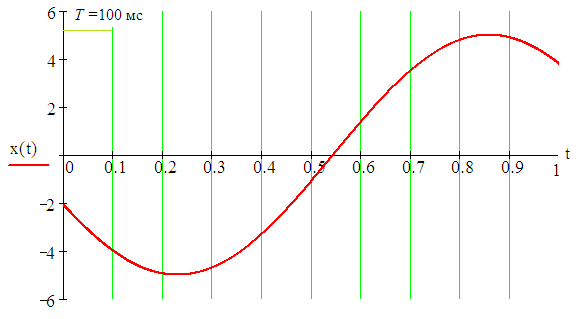мс болса, оны жасыл тік сызықтар арқылы белгілейміз.


Дискреттеу периодын орнату
Егер модуляцияланған сигналдың ұзақтығы 50 мс болса, онда ол дискреттеу периодының жартысын алады. Сонда сигналдың амплитудасы өзгермесе, ал ұзақтығы дискреттеу периодының жартысын алса, амплитудалық-импульстік модуляцияланған (АИМ) дискреттік сигналдың графигі төмендегідей болады.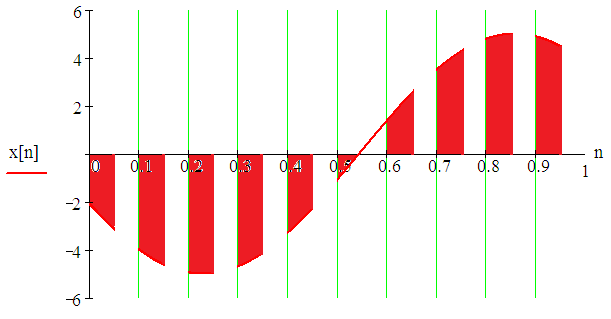


АИМ дискреттік сигналдың графигі
Есептің шешімі 3-суретте көрсетілген дискреттік сигналдың графигі болып есептеледі.
Өзіндік жұмысқа арналған тапсырмалар:
Есеп 1. Төмендегі сигналдың ЕИМ дискреттік сигналын құрастырып, оның графигін орындап беріңіз. Дискреттік сигналдың дискреттеу периоды 1 с, ал ЕИМ сигналының амплитудасы 300 мВ болсын.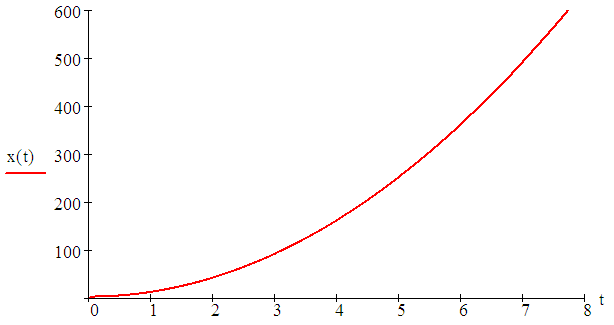


Үздіксіз сигнал графигі
Есеп 2. Төмендегі сигналдың ЕИМ дискреттік сигналын құрастырып, оның графигін орындап беріңіз. Дискреттік сигналдың дискреттеу периоды 1 с, ал ЕИМ сигналының амплитудасы 2 мВ болсын.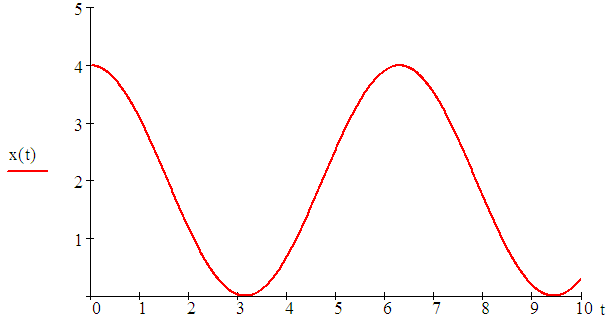


Үздіксіз сигнал графигі
Есеп 3. Төмендегі сигналдың АИМ дискреттік сигналын құрастырып, оның графигін орындап беріңіз. Дискреттік сигналдың дискреттеу периоды 1 с, ал АИМ сигналының импульс ені (ұзақтығы) 300 мс болсын.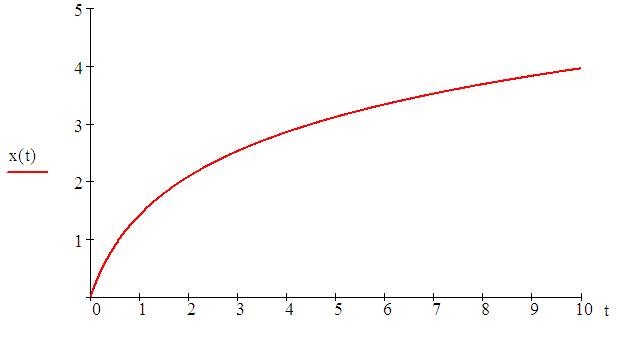


Үздіксіз сигнал графигі
Бақылау сұрақтары:

1. Дискретті автоматты реттеу жүйесі дегеніміз не?

2. Сигналдарды дискреттеудің қандай тәсілдері болады?

3. Сигналдарды кванттау мен модуляция арасында қандай айырмашылық бар?

4. Модуляцияның қандай түрлері болады?

5. Ендік модуляцияның негізгі принциптерін түсіндіріп беріңіз?

6. Амплитудалық модуляцияның негізгі принциптерін түсіндіріп беріңіз?

7. Уақыттық импульстік модуляция қалай жүзеге асады?
10-ТАҚЫРЫП. Дискретті және импульстік АРЖ математикалық анықталуы. Торлы функциялар
Практикалық сабақ жоспары:

1. Сабақтың басында көрсетілген мысалды талқылау.

2. Көрсетліген мысалдардағы әдістерді бекіту мақсатында берілген есептерді шығару.

3. Шығарылған есептердің шешімін талқылау.

4. Практикалық жұмыс бойынша есепті рәсімдеу және оларды оқытушыға тексеруге тапсыру.
Тапсырмалар:

Есеп 1. Берілген торлы функцияның алғашқы айырымдарын табу және олардың графиктерін құрастыру. Келесі торлы функция берілген:



Есептің шешімі. Торлы функцияның айырымын табу үшін оның аргументін бірге қосып, пайда болған функциядан бастапқы функцияны алып тастайды, яғни функцияның алғашқы айырымы келесідей есептеледі:





Торлы функцияның алғашқы айырымы Енді пайда болған функция үшін осы әдісті қолдана отырып, торлы функцияның екінші айырымын табуға болады:



Сонда функцияның екінші айырымы Соңғы пайда болған функцияда аргументі жойылғасын, берілген торлы функцияның тек екі айырымы болатыны байқауға болады. Енді торлы функцияның және оның айырымдарының графиктерін құрастырайық.

Төмендегі 1-суретте торлы функцияның өз графигі құрастырылған. Содан кейін торлы функцияның бірінші айырымы (Сурет 2) және екінші айырымы құрастырылған (Сурет 3).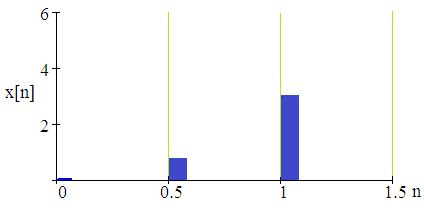


Торлы функцияның графигі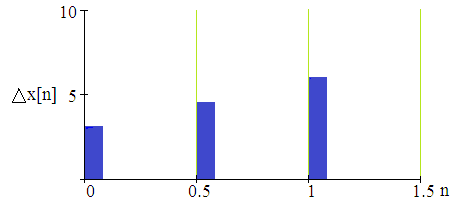


Торлы функцияның бірінші айырымы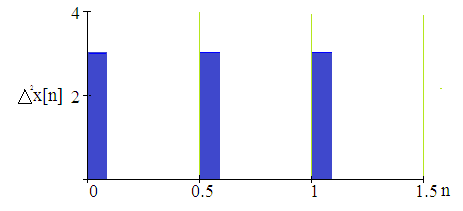


Торлы функцияның екінші айырымы
Көрсетілген графиктердегі функциялардың дискреттеу периоды 0,5 секундқа тең.
Өзіндік жұмысқа арналған тапсырмалар:

Есеп 1. Берілген торлы функцияның алғашқы екі айырымдарын табу және олардың графиктерін құрастыру. Келесі торлы функция берілген:


Есеп 2. Берілген торлы функцияның алғашқы екі айырымдарын табу және олардың графиктерін құрастыру. Келесі торлы функция берілген:


Есеп 3. Берілген торлы функцияның алғашқы екі айырымдарын табу және олардың графиктерін құрастыру. Келесі торлы функция берілген:


Есеп 4. Берілген торлы функцияның алғашқы екі айырымдарын табу және олардың графиктерін құрастыру. Келесі торлы функция берілген:


Есеп 5. Берілген торлы функцияның алғашқы екі айырымдарын табу және олардың графиктерін құрастыру. Келесі торлы функция берілген:


Бақылау сұрақтары:

1. Дискретті автоматты реттеу жүйесі дегеніміз не?

2. Торлы функция деген не? Ол не үшін қажет?

3. Торлы функцияның айырымы деген не?

4. Торлы функцияның айырымын қалай есептейді?

5. Айырымдардың түрлендіруін қалай жүргізеді?

6. Айырымдық теңдеу деген не?
11-ТАҚЫРЫП. Лапластың дискреттік түрлендіруі және оның қасиеттері. Z-түрлендіру
Практикалық сабақ жоспары:

1. Сабақтың басында көрсетілген мысалды талқылау.

2. Көрсетліген мысалдардағы әдістерді бекіту мақсатында берілген есептерді шығару.

3. Шығарылған есептердің шешімін талқылау.

4. Практикалық жұмыс бойынша есепті рәсімдеу және оларды оқытушыға тексеруге тапсыру.
Тапсырмалар:

Есеп 1. Берілген торлы функция ретінде берілген импульстік сигналдың дискреттік Лаплас түрлендіруінің (ДЛТ) негізінде кескінін табу қажет. Содан кейін осы сигналдың z-түрлендіруін да табу қажет.

Сигнал:
Есептің шешімі. ДЛТ формуласы келесідей болса



сигналдың кескінін келесідей етіп табайық:



Сигналдың z-түрлендіруін табу үшін пайда болған ДЛТ кескінінде келесі айнымалылардың алмастыруын орындау қажет Сонда z-түрлендіру бойынша сигналдың кескіні келесідей болады:


Есеп 2. Берілген торлы функция ретінде берілген импульстік сигналдың ДЛТ негізінде кескінін табу қажет. Содан кейін осы сигналдың z-түрлендіруін да табу қажет.

Сигнал:
Есептің шешімі. Тригонометриялық функциялардың ДЛТ кескінін дайындау үшін функцияның формуласын түрлендіру қажет, яғни келесі экспоненциялды түрге көшу қажет:



Сонда ДЛТ кескіні келесідей табылады:






Бөлшектің алымы мен бөлімін шамасына көбейтсек, сигналдың толық кескінін табамыз:


Сигналдың z-түрлендіру бойынша кескіні келесідей болады:


Өзіндік жұмысқа арналған тапсырмалар:

Есеп 1. Берілген торлы функция ретінде берілген импульстік сигналдың ДЛТ негізінде кескінін табу қажет. Содан кейін осы сигналдың z-түрлендіруін да табу қажет.

Сигнал:
Есеп 2. Берілген торлы функция ретінде берілген импульстік сигналдың ДЛТ негізінде кескінін табу қажет. Содан кейін осы сигналдың z-түрлендіруін да табу қажет.

Сигнал:
Есеп 3. Берілген торлы функция ретінде берілген импульстік сигналдың ДЛТ негізінде кескінін табу қажет. Содан кейін осы сигналдың z-түрлендіруін да табу қажет.

Сигнал:
Есеп 4. Берілген торлы функция ретінде берілген импульстік сигналдың ДЛТ негізінде кескінін табу қажет. Содан кейін осы сигналдың z-түрлендіруін да табу қажет.

Сигнал:
Есеп 5. Берілген сигналдың кескінінен оның түпнұсқасын табу қажет.

Сигнал:

Есеп 6. Берілген сигналдың кескінінен оның түпнұсқасын табу қажет.

Сигнал:
Бақылау сұрақтары:

1. Дискретті автоматты реттеу жүйесі дегеніміз не?

2. ДЛТ деген не?

3. Z-түрлендіру деген не?

4. Сигналдың түпнұсқасын табудың алгоритмі қандай?

5. Кері ДЛТ деген не?

6. Кері Z-түрлендіру қалай жасалады?

7. Z-түрлендіру мен ДЛТ арасында қандай байланыс бар?
12-ТАҚЫРЫП. Импульстік автоматты реттеу жүйелерді беріліс функциялар арқылы сипаттау әдістері
Практикалық сабақ жоспары:

1. Сабақтың басында көрсетілген мысалды талқылау.

2. Көрсетліген мысалдардағы әдістерді бекіту мақсатында берілген есептерді шығару.

3. Шығарылған есептердің шешімін талқылау.

4. Практикалық жұмыс бойынша есепті рәсімдеу және оларды оқытушыға тексеруге тапсыру.
Тапсырмалар:

Есеп 1. Егер импульстік автоматты реттеу жүйесі (АРЖ) төмендегі беріліс функция арқылы берілетін болса, кері z-түрлендіру арқылы оның импульстік сипаттамасын табу қажет:

АРЖ:

Есептің шешімі.

1. АРЖ полюстерін анықтаймыз. Ол үшін сипаттауыш теңдеудің түбірлерін табу қажет:

.

Квадрат теңдеуді шешу нәтижесіндегі түбірлер:

2. Табылған түбірлердің қалындысын келесі формула арқылы есептейміз:


2.1. түбір үшін:



2.2. түбір үшін:


Сонда АРЖ импульстік сипаттамасы екі түбірдің қалындысының қосындысы болып табылады:


Өзіндік жұмысқа арналған тапсырмалар:

Есеп 1. Егер импульстік автоматты реттеу жүйесі (АРЖ) төмендегі беріліс функция арқылы берілетін болса, кері z-түрлендіру арқылы оның импульстік сипаттамасын табу қажет:

АРЖ:

Есеп 2. Егер импульстік автоматты реттеу жүйесі (АРЖ) төмендегі беріліс функция арқылы берілетін болса, кері z-түрлендіру арқылы оның импульстік сипаттамасын табу қажет:

АРЖ:

Есеп 3. Егер импульстік автоматты реттеу жүйесі (АРЖ) төмендегі беріліс функция арқылы берілетін болса, кері z-түрлендіру арқылы оның импульстік сипаттамасын табу қажет:

АРЖ:

Есеп 4. Егер импульстік автоматты реттеу жүйесі (АРЖ) төмендегі беріліс функция арқылы берілетін болса, кері z-түрлендіру арқылы оның импульстік сипаттамасын табу қажет:

АРЖ:

Есеп 5. Егер импульстік автоматты реттеу жүйесі (АРЖ) төмендегі беріліс функция арқылы берілетін болса, кері z-түрлендіру арқылы оның импульстік сипаттамасын табу қажет:

АРЖ:
Бақылау сұрақтары:

1. Дискретті автоматты реттеу жүйесі дегеніміз не?

2. Импульстік сипаттама деген не?

3. Кері Z-түрлендіру деген не?

4. Сигналдың түпнұсқасын табудың алгоритмі қандай?

5. Импульстік АРЖ беріліс функциясы деген не?

6. Кері Z-түрлендіру қалай жасалады?

7. Z-түрлендіру мен ДЛТ арасында қандай байланыс бар?
13-ТАҚЫРЫП. Импульстік жүйелерді қосу, жинау және салыстырмалы түрде сараптау
Практикалық сабақ жоспары:

1. Сабақтың басында көрсетілген мысалды талқылау.

2. Көрсетліген мысалдардағы әдістерді бекіту мақсатында берілген есептерді шығару.

3. Шығарылған есептердің шешімін талқылау.

4. Практикалық жұмыс бойынша есепті рәсімдеу және оларды оқытушыға тексеруге тапсыру.
Тапсырмалар:

Есеп 1. Егер импульстік автоматты реттеу жүйесі (АРЖ) төмендегідей сұлба арқылы берілсе, жүйенің толық беріліс функциясын табыңыз.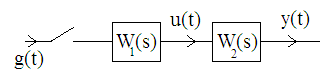


АРЖ: ,
Есептің шешімі.

1. Екі үздіксіз буын тізбектей қосылғасын жерде және олардың арасында кванттау кілті жоқ болғасын жерде олардың беріліс функцияларын көбейтеміз:



2. Содан кейін осы пайда болған буынның импульстік нұсқасын келесі формула арқылы есептеу қажет: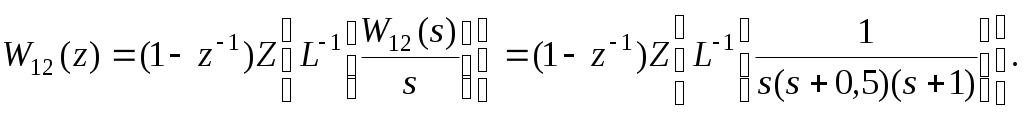



2.1. Беріліс функцияның кері Лаплас түрлендіруін анықтау қажет:



Белгісіз коэффициенттер оңай есептеледі: Түпнұсқа келесідей:



2.2. Енді соңғы түпнұсқадан z-түрлендіру операциясын орындау қажет:



2.3. Толық импульстік беріліс функция формулаға сәйкес келесідей болады:


Есетің жауабы:
Өзіндік жұмысқа арналған тапсырмалар:

Есеп 1. Егер импульстік АРЖ төмендегідей сұлба арқылы берілсе, жүйенің толық беріліс функциясын табыңыз.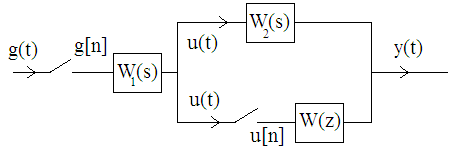



АРЖ:
Есеп 2. Егер импульстік АРЖ төмендегідей сұлба арқылы берілсе, жүйенің толық беріліс функциясын табыңыз.



АРЖ:
Есеп 3. Егер импульстік АРЖ төмендегідей сұлба арқылы берілсе, жүйенің толық беріліс функциясын табыңыз.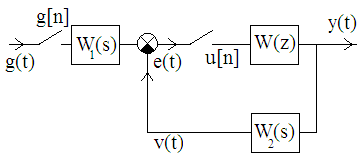


АРЖ:

Бақылау сұрақтары:

1. Дискретті автоматты реттеу жүйесі дегеніміз не?

2. Импульстік сипаттама деген не?

3. Үздіксіз буынның импультстік нұсқасы қалай табылады?

4. Сигналдың түпнұсқасын табудың алгоритмі қандай?

5. Импульстік АРЖ қосу түрлері қандай болып келеді?

6. Кері байланыс импльстік АРЖ үшін қалай жасалады?

7. Z-түрлендіру мен дискреттік Лаплас түрлендіруі арасында қандай байланыс бар?
14-ТАҚЫРЫП. Амплитудалық импульсті модуляциясы бар импульстік жүйелердің орнықтылығын зерттеу. Орнықтылықтың алгебралық критерийі
Практикалық сабақ жоспары:

1. Сабақтың басында көрсетілген мысалды талқылау.

2. Көрсетілген мысалдардағы әдістерді бекіту мақсатында берілген есептерді шығару.

3. Шығарылған есептердің шешімін талқылау.

4. Практикалық жұмыс бойынша есепті рәсімдеу және оларды оқытушыға тексеруге тапсыру.
Тапсырмалар:

Есеп 1. Егер импульстік автоматты реттеу жүйесінің (АРЖ) беріліс функциясы төмендегі теңдеумен берілсе, жүйенің орнықтылығын алгебралық критерий (Гурвиц критерийінің аналогы) арқылы зерттеу қажет.
АРЖ: .

Есептің шешімі.

1. Жүйенің сипаттауыш теңдеуін бөлек жазып аламыз:



2. Содан кейін Мебиус түрлендіруін жасаймыз да, жаңа сипаттауыш теңдеу құрастырамыз:

,

2.1. Теңдеудің ортақ бөлімін табамыз және алымын жаңа сипаттауыш теңдеу ретінде қарастырамыз:

,

.

2.2. Теңдеуді жақшаларды ашу арқылы ықшамдағаннан кейін ол келесідей түрде болады:

немесе .

3. Енді Гурвиц матрицасын құрастыру қажет қажет: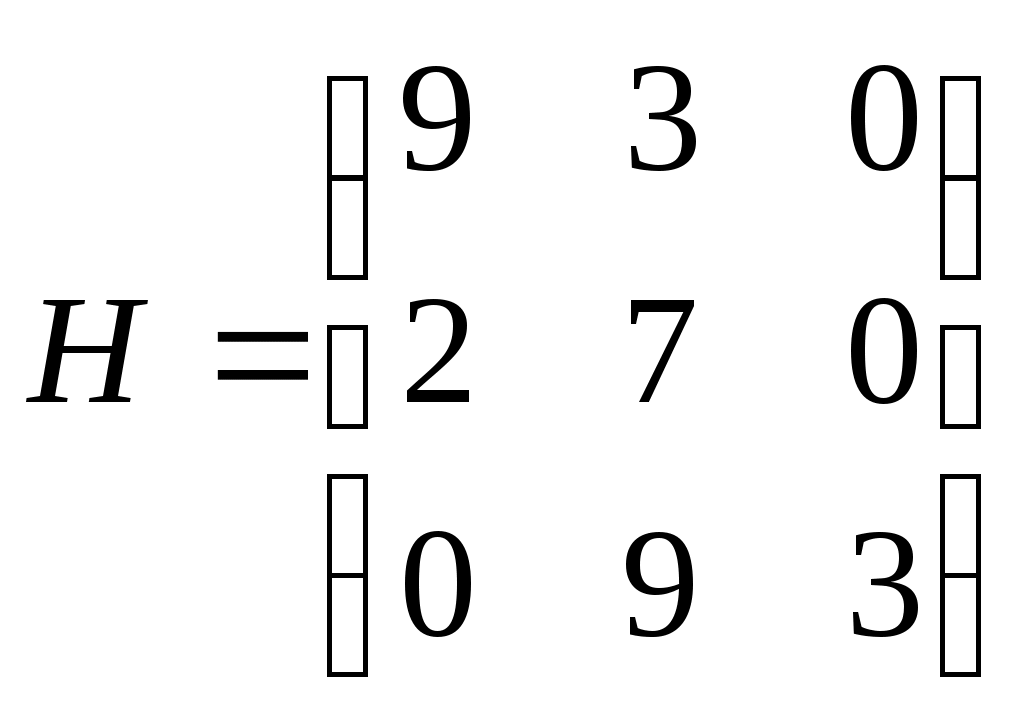

.

3.1. Гурвиц матрицасының барлық диагональдық минорларын есептеу қажет: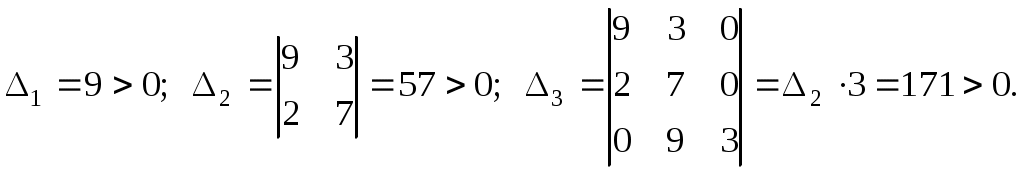



Барлық диагональдық минорлардың мәндері оң болғасын, импульстік АРЖ орнықты деп тұжырым жасаймыз.

Есетің жауабы: Жүйе орнықты.
Өзіндік жұмысқа арналған тапсырмалар:

Есеп 1. Егер импульстік автоматты реттеу жүйесінің (АРЖ) беріліс функциясы төмендегі теңдеумен берілсе, жүйенің орнықтылығын алгебралық критерий (Гурвиц критерийінің аналогы) арқылы зерттеу қажет.

АРЖ: .

Есеп 2. Егер импульстік автоматты реттеу жүйесінің (АРЖ) беріліс функциясы төмендегі теңдеумен берілсе, жүйенің орнықтылығын алгебралық критерий (Гурвиц критерийінің аналогы) арқылы зерттеу қажет.

АРЖ: .

Есеп 3. Егер импульстік автоматты реттеу жүйесінің (АРЖ) беріліс функциясы төмендегі теңдеумен берілсе, жүйенің орнықтылығын алгебралық критерий (Гурвиц критерийінің аналогы) арқылы зерттеу қажет.

АРЖ: .

Есеп 4. Егер импульстік автоматты реттеу жүйесінің (АРЖ) беріліс функциясы төмендегі теңдеумен берілсе, жүйенің орнықтылығын алгебралық критерий (Гурвиц критерийінің аналогы) арқылы зерттеу қажет.

АРЖ: .
Бақылау сұрақтары:

1. Дискретті автоматты реттеу жүйесі дегеніміз не?

2. Импульстік сипаттама деген не?

3. Импульстік АРЖ орнықтылығының негізгі шарттары қандай?

4. Алгебралық орнықтылық критерийінің негізгі қадамдары қандай?

5. Мебиус түрлендіруін неге қолданады?

6. Гурвиц матрицасын қалай құрастырады?

7. Қандай жағдайда импульстік АРЖ орнықытылық шекарасында болады?
15-ТАҚЫРЫП. Амплитудалық импульсті модуляциясы бар импульстік жүйелердің орнықтылығын зерттеу. Орнықтылықтың жиіліктік критерийі
Практикалық сабақ жоспары:

1. Сабақтың басында көрсетілген мысалды талқылау.

2. Көрсетілген мысалдардағы әдістерді бекіту мақсатында берілген есептерді шығару.

3. Шығарылған есептердің шешімін талқылау.

4. Практикалық жұмыс бойынша есепті рәсімдеу және оларды оқытушыға тексеруге тапсыру.
Тапсырмалар:

Есеп 1. Егер импульстік автоматты реттеу жүйесінің (АРЖ) беріліс функциясы төмендегі теңдеумен берілсе, жүйенің орнықтылығын графикалық-аналитикалық критерий (Михайлов критерийінің аналогы) арқылы зерттеу қажет.
АРЖ: .
Есептің шешімі.

1. Жүйенің сипаттауыш теңдеуін бөлек жазып аламыз:



2. Содан кейін түрлендіруін жасаймыз да, жаңа сипаттауыш теңдеуден сипаттауыш кешен құрастырамыз:



2.1. Эйре теңдеуін ескеру арқылы сипаттауыш кешенді түрлендіреміз:



.
2.2. Кешеннің нақты және жорамал бөліктерін жеке жазып шығамыз:
және .
3. Енді бұрыштың мәндерін аралығында өзгерту арқылы, кешеннің нақты және жорамал бөліктерін есептейміз. Годографты тұрғызуымыз қажет:

	0	30	60	90	120	150	180
	1,75	0,43	-1,708	1,086	0,618	0,23	0,731
	0	0,058	-1,396	1,12	1,07	-0,89	-1,627

3.1. Енді комплексті жазықтық бетіне осы годографты тұрғызу қажет: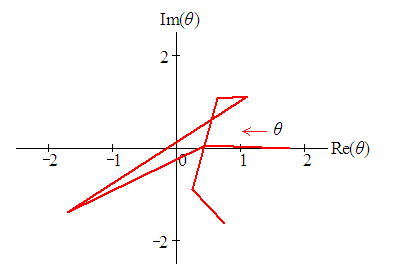

Орнықты АРЖ үшін годограф оң нақты осьте басталып, тізбектей 2N ширекті өтіп шығуы қажет, мұндағы N – жүйенің дәрежесі. Яғни осы есептің шарты бойынша годограф 6 ширекті тізбектей өтіп шығу қажет. Суреттен көріп отырғандай, годограф тізбектей ширектерді өтіп шыққан жоқ, сондықтан АРЖ орнықсыз.

Есетің жауабы: Жүйе орнықсыз.
Өзіндік жұмысқа арналған тапсырмалар:
Есеп 1. Егер импульстік автоматты реттеу жүйесінің (АРЖ) беріліс функциясы төмендегі теңдеумен берілсе, жүйенің орнықтылығын графикалық-аналитикалық критерий (Михайлов критерийінің аналогы) арқылы зерттеу қажет.

АРЖ: .

Есеп 2. Егер импульстік автоматты реттеу жүйесінің (АРЖ) беріліс функциясы төмендегі теңдеумен берілсе, жүйенің орнықтылығын графикалық-аналитикалық критерий (Михайлов критерийінің аналогы) арқылы зерттеу қажет.

АРЖ: .

Есеп 3. Егер импульстік автоматты реттеу жүйесінің (АРЖ) беріліс функциясы төмендегі теңдеумен берілсе, жүйенің орнықтылығын графикалық-аналитикалық критерий (Михайлов критерийінің аналогы) арқылы зерттеу қажет.

АРЖ: .

Есеп 4. Егер импульстік автоматты реттеу жүйесінің (АРЖ) беріліс функциясы төмендегі теңдеумен берілсе, жүйенің орнықтылығын графикалық-аналитикалық критерий (Михайлов критерийінің аналогы) арқылы зерттеу қажет.

АРЖ: .

Есеп 5. Егер импульстік автоматты реттеу жүйесінің (АРЖ) беріліс функциясы төмендегі теңдеумен берілсе, жүйенің орнықтылығын графикалық-аналитикалық критерий (Михайлов критерийінің аналогы) арқылы зерттеу қажет.

АРЖ: .
Бақылау сұрақтары:

1. Дискретті автоматты реттеу жүйесі дегеніміз не?

2. Импульстік сипаттама деген не?

3. Импульстік АРЖ орнықтылығының негізгі шарттары қандай?

4. Графикалық-аналитикалық орнықтылық критерийінің негізгі қадамдары қандай?

5. Эйлер формуласын не үшін қолданады?

6. Годограф қанша ширекті өтіп шығу қажет және неге?

7. Қандай жағдайда импульстік АРЖ орнықытылық шекарасында болады?