пОЯСНИТЕЛЬНАЯ ЗАПИСКА ПО КУРСОВОМУ ПРОЕКТУ ЖБК, ПГС. 2 ПЗ КП ОБРАЗЕЦ (Восстановлен) (Восстановлен1). Железобетонные конструкции многоэтажного каркасного здания
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
|
РАСЧЕТ И КОНСТРУИРОВАНИЕ ОДНОПРОЛЕТНОГО РИГЕЛЯ Для опирания пустотных панелей принимается сечение ригеля высотой hb =60 см. Ригели могут выполняться обычными или предварительно напряженными. Исходные данные Нормативные и расчетные нагрузки на 1 м2перекрытия принимаются те же, что и при расчете панели перекрытия. Ригель шарнирно оперт на консоли колонны, hb= 60 см. Расчетный пролет (рис. 6): 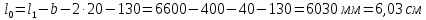 где 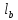 - пролет ригеля в осях; - пролет ригеля в осях;b– размер колонны; 20 - зазор между колонной и торцом ригеля; 130 – размер площадки опирания. Расчетная нагрузка на 1 м длины ригеля определяется с грузовой полосы, равной шагу рам, в данном случае шаг рам 7,4 м. (рис. 1) Постоянная нагрузка (табл. 1): - от перекрытия с учетом коэффициента надежности по ответственности здания 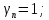 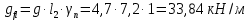 - от веса ригеля: 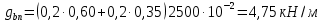 где 2500 кг/м3– плотность железобетона. С учетом коэффициента надежности по нагрузке 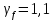 и по ответственности здания и по ответственности здания 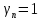 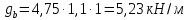 Итого постоянная нагрузка погонная, т.е. с грузовой полосы, равной шагу рам: 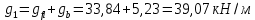 Временная нагрузка (ʋ1) с учетом коэффициента надежности по ответственности здания 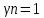 и коэффициента сочетания (см. табл.1). и коэффициента сочетания (см. табл.1).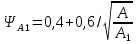 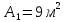 - для помещений указанных с поз. 1, 2, 12 [1]; - для помещений указанных с поз. 1, 2, 12 [1];А – грузовая площадь ригеля; А = 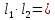 6,6×7,2 = 47,52 м2 6,6×7,2 = 47,52 м2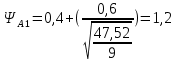 На коэффициент сочетания умножается нагрузка без учета перегородок: 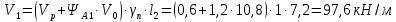 Полная расчетная погонная нагрузка на ригель: 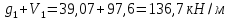 .; .;  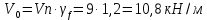  Рисунок 6 – Расчетный пролет ригеля  Рисунок 7 – Расчетное сечение ригеля Рисунок 7 – Расчетное сечение ригеля3.1 Определение усилий в ригеле Расчетная схема ригеля – однопролетная шарнирно опертая балка пролетом 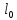 . Вычисляем значение максимального изгибающего момента М и максимальной поперечной силы Q от полной расчетной нагрузки: . Вычисляем значение максимального изгибающего момента М и максимальной поперечной силы Q от полной расчетной нагрузки: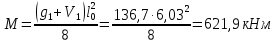 . .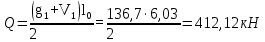 . .Характеристики прочности бетона и арматуры: - Бетон тяжелый класса B15: 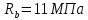 ; ; 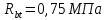 ; ;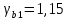 ; ; - Арматура: - продольная ненапрягаемая класса А400 диаметром 10-40 мм: 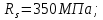 - поперечная ненапрягаемая класса А400 диаметром 6-8мм: 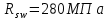 3.2 Расчет ригеля по прочности нормальных сечений при действии изгибающего момента Определяем высоту сжатой зоны 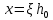 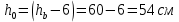 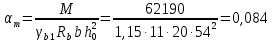 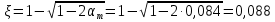 ; ;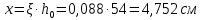 . .Граница сжатой зоны проходит в узкой части сечения ригеля, следовательно, расчет ведем как для прямоугольного сечения. Расчет по прочности нормальных сечений производится в зависимости от соотношения относительной высоты сжатой зоны бетона и граничной относительной высоты ξR, при которой предельное состояние элемента наступает по сжатой зоне бетона одновременно с достижением в растянутой арматуре напряжения, равного расчетному сопротивлению Rs Значение ξR определяется по формуле: 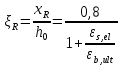 где, 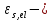 относительная деформация растянутой арматуры при напряжениях, равных Rs; относительная деформация растянутой арматуры при напряжениях, равных Rs;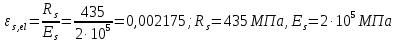 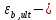 относительная деформация сжатого бетона при напряжениях равных Rb, принимаемая равной 0,0035 (п. 6.2.7 [3]): относительная деформация сжатого бетона при напряжениях равных Rb, принимаемая равной 0,0035 (п. 6.2.7 [3]): 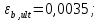 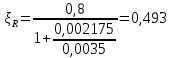 значение ξR можно определить по табл. 3.2 [5] или по Приложению 11. Т.к. ξ=0,481 < ξR=0,493, площадь сечения растянутой арматуры определяется по формуле: 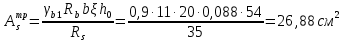 Подбираем 6Ø25 А400 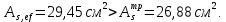 Определим процент армирования поперечного сечения ригеля: 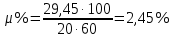 . .3.3 Расчет ригеля по прочности при действии поперечных сил Расчёт ригеля по прочности при действии поперечных сил производится на основе модели наклонных сечений [3]. Ригель опирается на колонну с помощью консолей, скрытых в его подрезке, т.е. имеет место резко изменяющаяся высота сечения ригеля на опоре. Для ригелей с подрезками на опорах производится расчёт по поперечной силе для наклонных сечений, проходящих у опоры консоли, образованной подрезкой. При этом в расчётные формулы вводится рабочая высота h01короткой консоли ригеля. Таким образом, в качестве расчётного, принимаем прямоугольное сечение с размерами b × h1= 20×30 см, в котором действует поперечная сила Q=174,92кН от полной расчётной нагрузки. Рабочая высота сечения ригеля в подрезке составляет 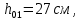 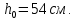 При диаметре нижних стержней продольной рабочей арматуры ригеля ds=22мм с учётом требований п.8.3.10 [3] назначаем поперечные стержни (хомуты) 2Ø6 А400. Их шаг на приопорном участке предварительно принимаем по конструктивным соображениям sw1=10 см, что в соответствии с п.8.3.11[3] не превышает 0,5h01=13,5 см и 30 см. Значения прочностных характеристик бетона класса В20, входящие в расчётные зависимости, принимаем с учётом коэффициента условий работы 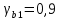 . .Расчёт ригеля по бетонной полосе между наклонными трещинами производится из условия: 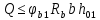 , ,где 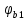 - коэффициент, принимаемый равным 0,3. - коэффициент, принимаемый равным 0,3.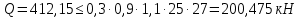 т.е. принятые размеры сечения ригеля в подрезке достаточны. Проверяем, требуется ли поперечная арматура по расчёту, из условия: 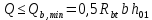 т.е. 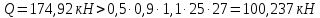 Расчет поперечной арматуры необходим. Находим погонное усилие в хомутах для принятых выше параметров поперечного армирования Asw=0,57 см2 (2Ø6 А500) , Rsw=300 МПа, sw1= 10 см: 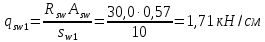 Расчёт ригеля с рабочей поперечной арматурой по наклонному сечению производится из условия: 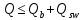 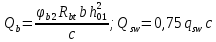 где с − длина проекции наклонного сечения на продольную ось элемента, 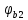 − коэффициент, принимаемый равным 1,5 (п. 6.2.34 [3]). − коэффициент, принимаемый равным 1,5 (п. 6.2.34 [3]).Наиболее опасная длина проекции наклонного сечения: 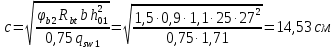 которая должна быть не более 2h01= 54 см. С учётом этой величины условие ( 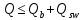 ) преобразуем к виду: ) преобразуем к виду: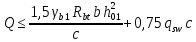 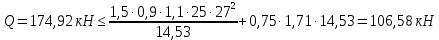 т.е. условие прочности ригеля по наклонному сечению в подрезке при действии поперечной силы не соблюдается. Ставим отгибы 2 Ø20 А400. Необходимо также убедиться в том, что принятый шаг хомутов не превышает максимального шага хомутов, при котором ещё обеспечивается прочность ригеля по наклонному сечению между двумя соседними хомутами, т.е. 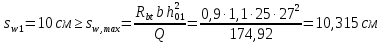 Примем, согласно п.8.3.11 [3], шаг хомутов в средней части пролёта равным 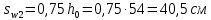 , что не превышает 500 мм. , что не превышает 500 мм. Погонное усилие в хомутах для этого участка составляет: 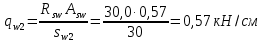 что не меньше минимальной интенсивности этого усилия, при которой поперечная арматура учитывается в расчёте: 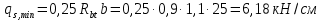 При действии на ригель равномерно распределённой нагрузки q=g1+v1длина участка с интенсивностью усилия в хомутах qsw,1 принимается не менее значения l1, определяемого по формуле: 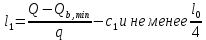 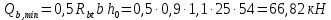 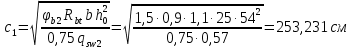 Поскольку 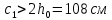 , то принимаем , то принимаем 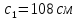 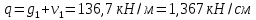 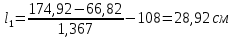 В ригелях с подрезками у концов последних устанавливаются дополнительные хомуты и отгибы для предотвращения горизонтальных трещин отрыва у входящего угла подрезки. Эти хомуты и отгибы должны удовлетворять условию: 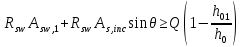 Для рассматриваемого примера со сравнительно небольшим значением поперечной силы примем дополнительные хомуты у конца подрезки в количестве 2Ø12 А500С с площадью сечения Asw 1=2,26 см2 Тогда проверка условия даёт: 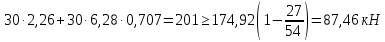 т.е. установленных дополнительных хомутов и отгибов достаточно для предотвращения горизонтальных трещин отрыва у входящего угла подрезки. 3.4 Построение эпюры материалов Продольная рабочая арматура в пролете 2Ø22 и 2Ø22 А400. Площадь этой арматуры Аs определена из расчета на действие максимального изгибающего момента в середине пролета. В целях экономии арматуры по мере уменьшения изгибающего момента к опорам два стержня обрываются в пролете, а два других доводятся до опор. Если продольная рабочая арматура разного диаметра, то до опор доводятся два стержня большего диаметра. Определяем изгибающий момент, воспринимаемый сечением ригеля с полной запроектированной арматурой 4Ø22 А400 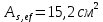 . .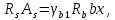 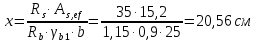 Изгибающий момент, воспринимаемый сечением ригеля, определяется из условия равновесия: 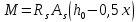 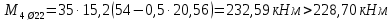 До опоры доводятся 3Ø22 А400, h0 = 60 – 3 = 57 см , 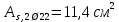 . .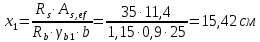 Определяем изгибающий момент, воспринимаемый сечением ригеля с рабочей арматурой в виде двух стержней, доводимых до опоры 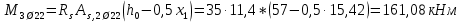 Откладываем в масштабе на эпюре моментов полученные значения изгибающих моментов М(2Ø22) и М(4Ø22) и определяем место теоретического обрыва рабочей арматуры – это точки пересечения эпюры моментов с горизонтальной линией, соответствующей изгибающему моменту, воспринимаемому сечением ригеля с рабочей арматурой в виде двух стержней М(2Ø22) (рис. 8). Изгибающий момент в любом сечении ригеля определяется по формуле 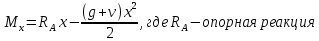 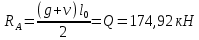 При 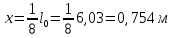 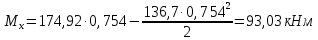 При 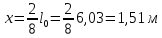 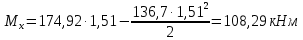 При 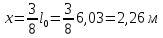 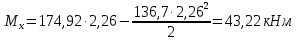  Рисунок 8 – Эпюра материалов в ригеле Длина анкеровки обрываемых стержней определяется по следующей зависимости:  Поперечная сила Q определяется графически в месте теоретического обрыва, Q1= 380 кН. Поперечные стержни 2Ø7 А400 Rsw= 300 МПа с Аsw= 0,77 см2 в месте теоретического обрыва имеют шаг 10 см; 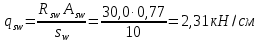 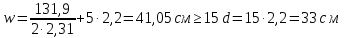 Принимаем W=59 см. Место теоретического обрыва арматуры можно определить аналитически. Для этого общее выражение для изгибающего момента нужно приравнять моменту, воспринимаемому сечением ригеля с арматурой 2Ø22 А400. 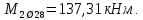 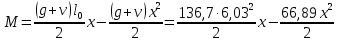 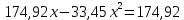 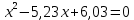 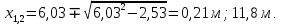 Это точки теоретического обрыва арматуры. Длина обрываемого стержня будет равна: 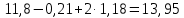 м. м.Определяем аналитически величину поперечной силы в месте теоретического обрыва арматуры при 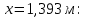 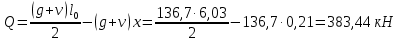 Это значение приблизительно совпадает с графически определенным 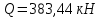 . . |
