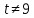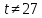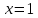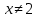К апелляции. К апелляции! Самые решаемые задания 12, 14, 18. Задание 12
 Скачать 0.94 Mb. Скачать 0.94 Mb.
|
|
К апелляции! Самые решаемые задания – 12, 14, 18. Задание 12 Важно помнить: любая ошибка в тригонометрии – 0 баллов; если пункт а) оценили 0 баллов, то пункт б) не проверяется (даже если выпускник сделал ошибку в записи ответов простейшего тригонометрического уравнения, но отбор корней на тригонометрической окружности проводит верно, последние действия не оцениваются). Нет смысла идти на апелляцию, если: 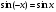 ; ;неправильно найдены корни квадратного уравнения; 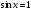 , , 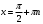 , , 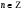 ; ;перепутал значения тригонометрических функций; при отборе корней через неравенства – неправильное решение неравенства относительно k (n, m), не полный перебор значений этих переменных; при использовании метода перебора значений целых n – написаны только подходящие значения n, дающие правильные ответы, но не обосновано, что других решений нет (нет отбора!); при отборе корней с помощью тригонометрической окружности не выделен отрезок, не подписаны точки или точки подписаны 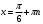 . .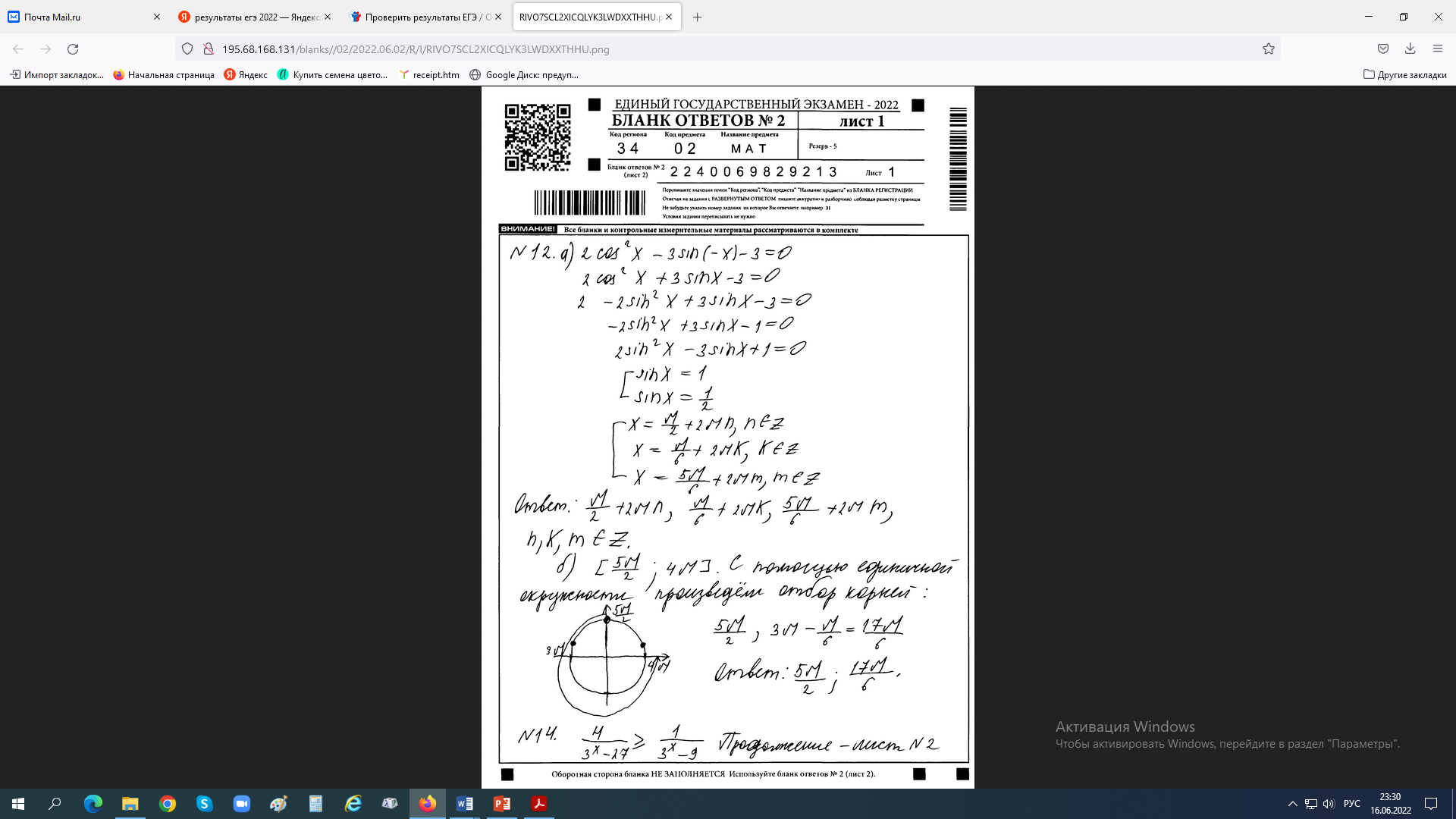 14 задание Решите неравенство 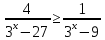 Подавляющее большинство решали данное неравенство методом интервалов, выполнив алгоритм: Найти область определения функции 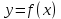 ; ;Найти нули данной функции; Определить знаки значений функции 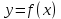 на каждом из промежутков, на которые нули функции разбивают область её определения; на каждом из промежутков, на которые нули функции разбивают область её определения;Выбрать нужные промежутки согласно знаку неравенства. Рассмотрим решение данного неравенства методом интервалов: 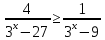 Сделаем замену 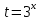 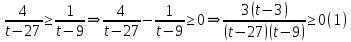 Рассмотрим функцию 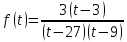 : :Область определения функции: 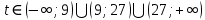 Нули функции: 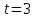 Определив знак значения функции на каждом получившемся промежутке, находим решение промежуточного неравенства (1): 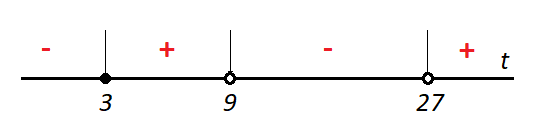 Получим совокупность неравенств 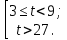 Сделаем обратную замену и решим получившиеся неравенства 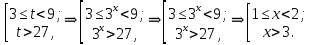 Ответ: 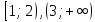 . .Получен верный ответ, но решение оценено – 0 баллов Пример 1. Имеем неравенство 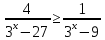 С самого начала участник записал ОДЗ для переменной в неравенстве 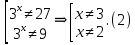 Сделал замену 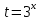 и получил неравенство и получил неравенство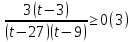 А затем, ничего не написав про значения 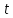 , участник переходит к неравенству , участник переходит к неравенству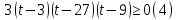 Решив его 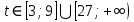 и подставив обратно переменную и подставив обратно переменную 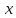 , получил множество , получил множество 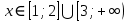 . Учтя условие (2), выпускник получил верный ответ, но за решение получил 0 баллов, так как неверно решил промежуточное неравенство (3). . Учтя условие (2), выпускник получил верный ответ, но за решение получил 0 баллов, так как неверно решил промежуточное неравенство (3).Пример 2. Имея неравенство 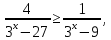 школьник получил неравенство 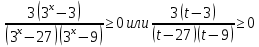 и собрался решать неравенство методом интервалов, начав рассматривать функцию 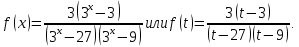 Но вместо того, чтобы найти область определения функции, школьник написал «найдём нули функции» и затем записал совокупность равенств 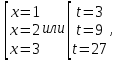 что является ошибочным использованием математического термина («нуль функции») – 0 баллов. 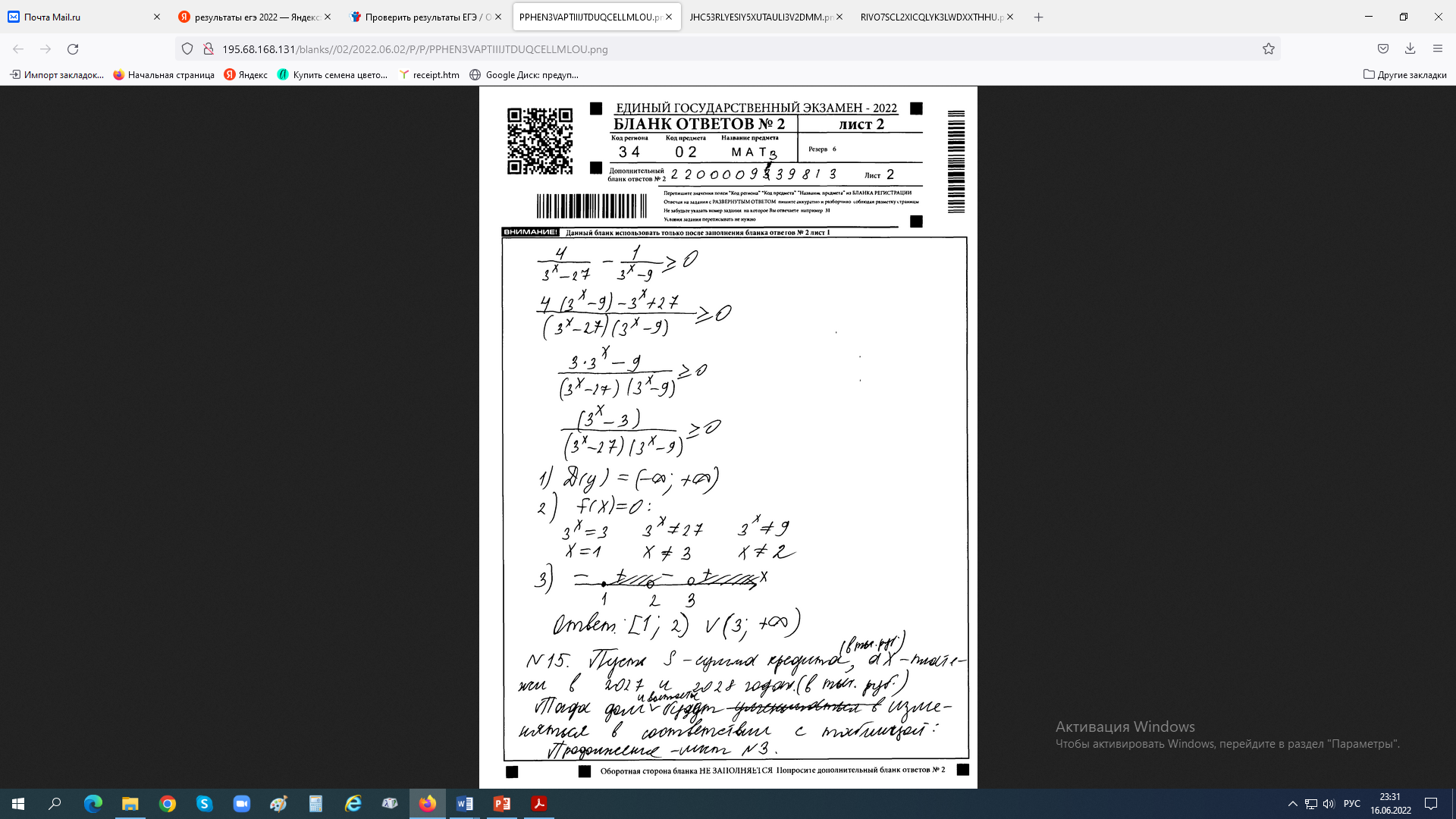 Пример 3. При решении того же неравенства 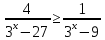 было получено новое неравенство после правильной замены 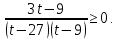 Затем школьник пишет 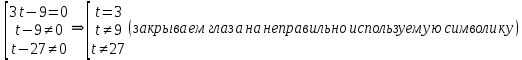 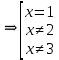 и определяет знаки (другой какой-то) функции 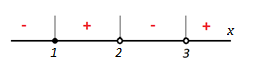 и записывает ответ 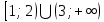 . . Пример 4. В неравенстве 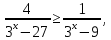 сделав замену 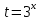 и получив неравенство и получив неравенство  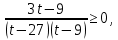 школьник затем пишет
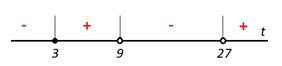  и даёт верный ответ 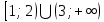 . Как получились именно такие знаки для второй картинки, переносом? Нет решения простейших показательных неравенств. А если бы основание показательной функции было 0,3, знаки на второй картинке изменились? . Как получились именно такие знаки для второй картинки, переносом? Нет решения простейших показательных неравенств. А если бы основание показательной функции было 0,3, знаки на второй картинке изменились?Пример 5. Были работы, в которых выпускник решал неравенство методом рационализации. Соответственно от неравенства 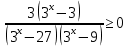 был сделан переход к неравенству 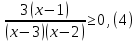 не сказав ни слова о тот, как основание показательной функции сравнивается с единицей или не дописав нужные множители 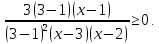 Ведь если неравенство было бы другим, например: 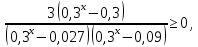 то переход к неравенству (4) был бы неверным, а учитывал ли выпускник тот факт, что основание больше единицы, или нет из решения непонятно. Что нужно было сделать: необходимо было отметить, что основание показательной функции равно 3, что больше единицы, или заменить множители вида 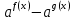 на знакотождественные произведения на знакотождественные произведения 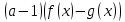 . .Пример 6. 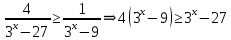 Переход неверный – 0 баллов. 18 задание В каких случаях не следует подавать апелляцию на решение задачи №18 1. Если, неверно поняли условие задачи и перекладывали по одному камню. Это относится и к ситуации, когда брали по камню из двух разных коробок и складывали в одну из этих двух коробок. В условии прописано, что камни нужно складывать в оставшуюся коробку. 2. Если обосновывали невозможность какой-то комбинации, ссылаясь на разную четность камней в коробках. Например, если в начале в коробках было 31, 50 и 0 камней. То переложив камни сначала в третью, а затем в первую коробку, мы получим комбинацию 32, 48, 1. Первые два числа стали четными. Но сделать их одинаковыми не удастся, поскольку у них разные остатки от деления на 3. Рассмотрим остатки от деления на 3 количеств камней в коробках. Изначально они равны: 1; 2; 0. После первого хода они будут равны: 0; 1; 2. После второго хода (любого) они будут равны: 2; 0; 1. После любого третьего хода остатки совпадут с первоначальными. Это означает, что достижимы только те комбинации количеств камней, у которых набор остатков от деления на 3 совпадает с одним из трех указанных (заметим, что, если при этом сумма совпадает с исходной, комбинация достижима). В частности, не достижима комбинация, при которой пусты первые две коробки, и комбинации, при которых в первой коробке один камень, а во второй менее двух камней. Четность здесь не причем! |