курсовой размерный анализ. К размерному анализу относятся вопросы
 Скачать 193.86 Kb. Скачать 193.86 Kb.
|
|
Введение Создание конструкций изделий должно удовлетворять требования к точности в целом и точности основных составляющих. Точностью основных составляющих решает размерный анализ конструкционных изделий. Размерный анализ технологического процесса - это выявление и фиксирование размерных связей между переходами и операциями конкретного технологического процесса. К размерному анализу относятся вопросы: Связанные с разработкой и анализом конструкций – определением и проверкой необходимых и достаточных требований, точности размеров, формы и взаимного расположения. Связанные с разработкой технологических процессов: расчеты номинальных и предельных значений технологических размеров, прогнозирование возможных значений припусков, назначение всех промежуточных размеров на обработку, вычисление оптимальной с точки зрения механической обработки простановки размеров. Связанные с анализом технологических процессов сборки – это проверка собираемости сборочных единиц, комплектов, изделий; выбор вида сборки по уровню взаимозаменяемости, обеспечение заданных значений выходных характеристик изделия. Целью размерного анализа является, прежде всего, обеспечение точности указанных на чертеже размерных связей между переходами и операциями конкретного технологического процесса. С помощью размерного анализа выявляется наиболее эффективная структура технологического процесса, гарантирующая достижение поставленной цели. В результате размерного анализа наиболее рационально формируются технологические операции и переходы, проверяются и уточняются принятые схемы базирования, определяются все операционные размеры и размеры исходной заготовки. Кроме того, размерный анализ позволяет выявить и устранить недопустимые колебания величины припуска, что особенно важно на финишных операциях. Вариант 3 1) Для заданных параллельно связанных размерных цепей (Рис. 1) А и Б по допускам и предельным отклонениям замыкающих звеньев найти допуски и предельные отклонения составляющих звеньев. Допуски замыкающих звеньев распределить между допусками составляющих звеньев произвольно. Задачу решить вероятностным методом в предположении о распределении размеров составляющих звеньев по закону равной вероятности и риске P=0,27%. 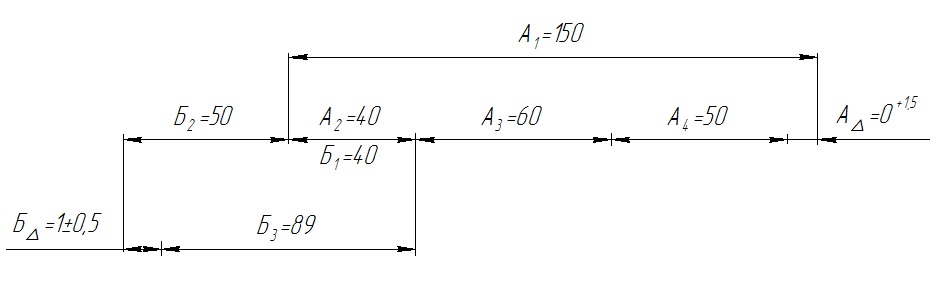 Рис. 1 Параллельно связанная цепь Решаем цепь с меньшим допуском замыкающего звена. Для ориентировочных оценок допусков составляющих звеньев определяем средний допуск 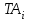 по формуле (1) : по формуле (1) :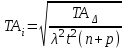 , (1) , (1)где 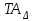 - допуск замыкающего звена; n, p - число увеличивающих и уменьшающих звенев; t∆ - коэффициент риска (Таблица 1); - допуск замыкающего звена; n, p - число увеличивающих и уменьшающих звенев; t∆ - коэффициент риска (Таблица 1); 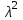 - относительное среднее квадратичное отклонение [1]. - относительное среднее квадратичное отклонение [1].Таблица 1 Ряд значений коэффициента
Значения коэффициента 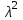 составляют: составляют:- при нормальном законе (законе Гаусса) распределения размеров составляющих звеньев 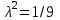 . .- при распределении по закону Симпсона (равнобедренного треугольника) 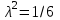 . .- при распределении по закону равной вероятности 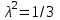 . .Если принять, что распределение размеров составляющих звеньев является нормальным по закону равной вероятности, то 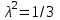 . При риске Р=0,27℅ коэффициент t∆=3.Допуск ТА∆=1,5,ТБ∆=1. . При риске Р=0,27℅ коэффициент t∆=3.Допуск ТА∆=1,5,ТБ∆=1.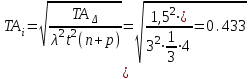 (1.1) (1.1)Назначаем верхние и нижние отклонения (одно звено оставляем неизвестным): 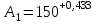 , ,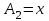 , , 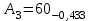 , ,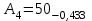 . .Расчет средних размеров: 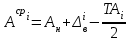 (2.1) (2.1)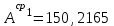 , ,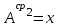 , , 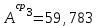 , ,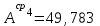 , ,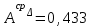 . .Составляем уравнение размерной цепи, оттуда находим неизвестное звено: 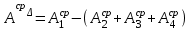 (3.1) (3.1)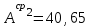 Верхнее и нижнее отклонение звена А3: 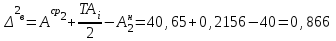 (4.1) (4.1)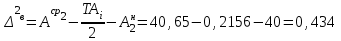 (5.1) (5.1)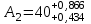 Вычисляем вторую цепь параллельно связанных размерных цепей: Формула (1) изменится, так как у нас известно, одно общее звено 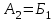 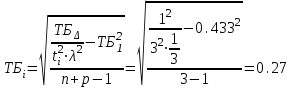 (6.1) (6.1)Назначаем верхние и нижние отклонения (одно звено оставляем неизвестным): 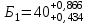 , ,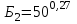 , , 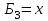 . .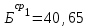 , ,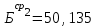 , , 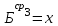 . .Составляем уравнение размерной цепи по формуле (3.1), оттуда находим неизвестное звено: 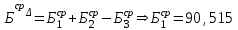 Верхнее и нижнее отклонение звена Б3: 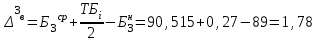 . . 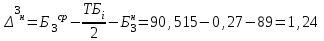 . .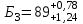 2) Точность замыкающего звена 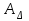 приведенной ниже (Рис. 2) размерной цепи обеспечивается методом групповой взаимозаменяемости при числе групп деталей N=4. Принимая расширенные допуски звеньев приведенной ниже (Рис. 2) размерной цепи обеспечивается методом групповой взаимозаменяемости при числе групп деталей N=4. Принимая расширенные допуски звеньев 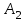 и и 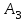 равными, определить допуски и координаты середин полей допусков составляющих звеньев, а также их номинальные значения и предельные отклонения в группах. равными, определить допуски и координаты середин полей допусков составляющих звеньев, а также их номинальные значения и предельные отклонения в группах. Рис. 2 Расширенный допуск замыкающего звена 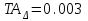  (2.1) (2.1)При распределении расширенного допуска замыкающего звена 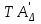 между составляющими звеньями необходимо, чтобы сумма допусков увеличивающих звеньев была равна сумме допусков уменьшающих звеньев (2.2): между составляющими звеньями необходимо, чтобы сумма допусков увеличивающих звеньев была равна сумме допусков уменьшающих звеньев (2.2): 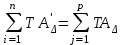 (2.2) (2.2)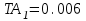 , , 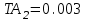 , , 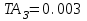 . .Координату середины поля допусков А3 найдем из уравнения(2.3): 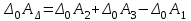 (2.3) (2.3)Отсюда: Для I группы: 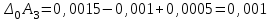 Для II группы: 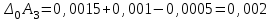 Для III группы: 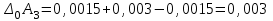 Для IV группы: 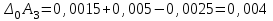 Таблица 2 Допуски и координаты середин полей допусков составляющих звеньев
3) Для показанной на рисунке 3 детали установлены технические требования: допуск перпендикулярности плоскости 2 относительно плоскости 1-0,01 мм; допуск параллельности плоскости 3 относительно плоскости 1 и плоскости 4 относительно плоскости 2 - 0,005 мм. Необходимо построить размерную цепь и определить отклонения от перпендикулярности плоскости 4 относительно плоскости 3. Задачу решить двумя методами: максимума-минимума и вероятностным в предложении о распределении отклонений расположения по нормальному закону и риске Р=1%. 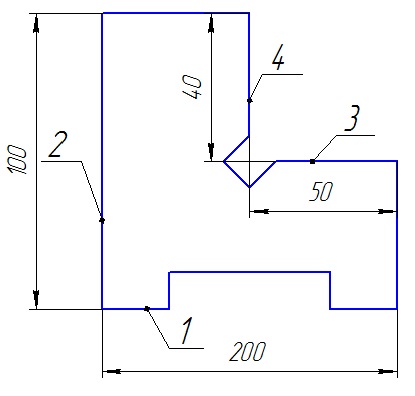 Рис. 3 N(2-1)=0±0.01 - допуск перпендикулярности плоскости 2 относительно плоскости 1. N(3-1)=0±0,005 - допуск перпендикулярности плоскости 3 относительно плоскости 1. Р(4-2)=0±0,005 - допуск параллельности плоскости 4 относительно плоскости 2. N(4-3)=? 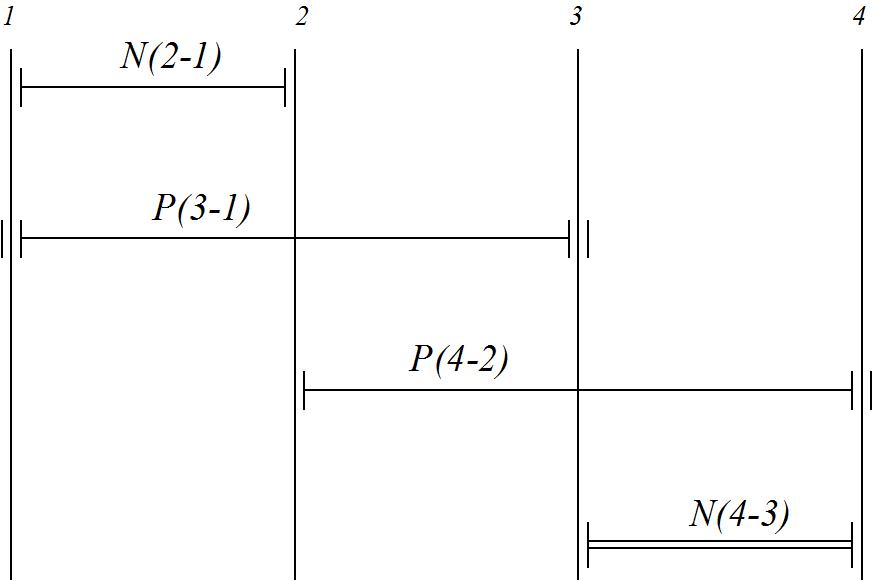 Рис. 4 Размерные цепи отклонений расположения для детали показанной на Рис. 3 1 - Метод максимума-минимума: Удельные отклонения: 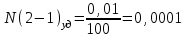 , ,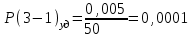 , ,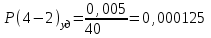 Удельное отклонение перпендикулярности плоскости 4 относительно плоскостей 3 определяется из уравнения: 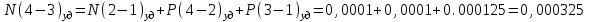 Абсолютное отклонение перпендикулярности плоскости 4 относительно плоскостей 2,3составит: 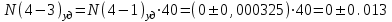 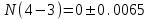 . .2 - Вероятностный метод: Если принять, распределение по закону Гауса то  . При риске Р=1% коэффициент t∆=2,6. (Таблица 1) . При риске Р=1% коэффициент t∆=2,6. (Таблица 1)Отклонение перпендикулярности плоскости 4 относительно плоскости 3 по вероятностным методом определяется по формуле: 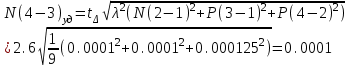 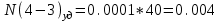 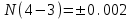 Вывод В результате проделанной курсовой работы были: 1. Приобретены навыки проведения размерного анализа конструкций машиностроительных изделий. 2. Освоена при выполнении чертежа программа САПР. 3. Решены задачи: 1) для параллельно связанных размерных цепей вероятностным методом; 2) для точности замыкающего звена 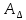 приведенной размерной цепи методом групповой взаимозаменяемости; 3) по точности расположения поверхности детали. приведенной размерной цепи методом групповой взаимозаменяемости; 3) по точности расположения поверхности детали. Список литературы 1. Скворцов В.Ф. Основы размерного анализа конструкций изделий. – Томск: Изд-во ТПУ, 2012. –80 с. (34 экз. электронный ресурс). 2. Скворцов В.Ф. Основы размерного анализа конструкций изделий. – Томск: Изд-во ТПУ, 2011. –80 с. 3. Размерный анализ технологических процессов / В. В. Матвеев, М. М. Тверской, Ф. И. Бойков и др. – М.: Машиностроение, 1982. – 264 с. 4. Васильев А.С., Дальский А.М., Золотаревский Ю.М., Кондаков А.И. Направленное формирование свойств изделий машиностроения / Под ред. д-ра техн. наук А.И. Кондакова. – М.: Машиностроение, 2005. 352 с.: ил. ISBN 5-217-03268-5. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
