Качество систем автоматики. Основные показатели
 Скачать 53.56 Kb. Скачать 53.56 Kb.
|
|
Качество систем автоматики. Основные показатели. Качество является одной из важнейших характеристик, определяющих эффективность автоматических систем регулирования. Чтобы управлять качеством сложных технических систем, необходимо установить показатели качества и уметь их оценивать (определять). Качество системы в общем виде можно представить некоторой функциональной зависимостью, зависящей от множества ее структурных, технических, аппаратных и эксплуатационных характеристик. Но решение такой задачи весьма сложно. На практике часто о качестве систем автоматического регулирования сложными технологическими процессами судят в первую очередь по их функциональным свойствам - совокупности точности в установившемся режиме и качества переходных процессов. Затухание переходных процессов в САУ, является необходимым, но далеко не достаточным условием практической пригодности системы. Необходимо учитывать такие показатели процессов регулирования, как длительность, колебательность, время первого согласования, собственную частоту колебаний и т.д. Качество регулирования численно может быть оценено прямыми показателями качества, которые можно определить непосредственно из кривых переходных процессов САУ. Проблема определения прямых показателей качества переходных процессов с математической точки зрения сводится к построению переходного процесса путем отыскания общего решения неоднородного дифференциального уравнения, описывающего систему при заданных начальных условиях и воздействиях, что для линейных стационарных систем не представляет больших трудностей. Но для систем, описываемых уравнениями выше третьего порядка или нелинейными, получить решение инженерными методами не всегда возможно или оно оказывается трудоемким. Поэтому в теории регулирования большое применение находят приближенные методы анализа переходных процессов по косвенным критериям качества, позволяющим оценить характеристики переходного процесса без непосредственного решения дифференциальных уравнений системы. К ним относятся три вида: частотные, корневые, интегральные. К основным прямым оценкам относятся следующие: δ-перерегулирование, tп - время регулирования, d - декремент затухания, ω0 - частота колебаний, n - число колебаний, которое имеет переходная характеристика за время регулирования tп, tр - время первого достижения установившегося значения переходного процесса, tm - время достижения первого максимума. Рассмотрим основные показатели качества систем управления, пользуясь характеристикой переходного процесса отработки единичного задающего воздействия g(t)=1(t), показанной на рисунке1. 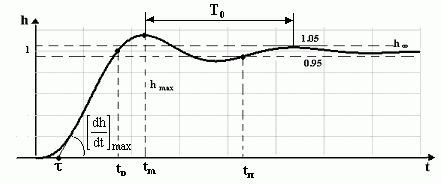 Рисунок1- Переходная характеристика h(t) Для оценки качества работы системы введены следующие показатели. 1. Время переходного процесса или полное время регулирована tп характеризует быстродействие системы и определяется как интервал времени от начала переходного процесса до момента, когда отклонение выходной величины от ее нового установившегося значения становится меньше определенной достаточно малой величины, обычно составляющей ± 5% от h. 2. Максимальное отклонение управляемой величины, соответствующее времени tm, от установившегося значения: где tm - время установления первого максимума управляемой величины, характеризующее скорость изменения ее в переходном процессе. Δдин представляет собой максимальную динамическую ошибку, определяющую точность системы в переходном процессе. 3. Перерегулирование определяется отношением максимального отклонения от установившейся величины в переходном процессе к установившемуся значению: 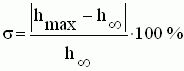 Перерегулирование характеризует склонность системы к колебаниям, то есть близость системы к колебательной границе устойчивости. В конечном итоге характеризует запасы устойчивости. Считается, что запас устойчивости достаточен, если лежит в пределах от 10 до 30%. 4. Время первого достижения регулируемой величиной заданного значения tр служит одной из оценок качества регулирования САУ и определяется как интервал времени от начала переходного процесса до момента, когда регулируемая величина впервые достигает заданного значения. 5. Колебательность переходного процесса обычно определяется числом колебаний, равным числу минимумов кривой переходного процесса в интервале [0, tп ] при ликвидации возмущения, или в случае отработки задания - числом перерегулирований за этот же интервал. Это число составляет обычно от 2 до 3. 5. Собственная частота колебаний системы 6. Логарифмический декремент затухания системы d, характеризующий быстроту затухания колебательного процесса, 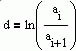 , где ai и ai+1 - две амплитуды рядом расположенных максимумов кривой переходного процесса. , где ai и ai+1 - две амплитуды рядом расположенных максимумов кривой переходного процесса.7. Максимальная скорость отработки управляемой величины (dh/dt)max=tgν. 8. Запаздывание в начале переходного процесса τ. 9. Статическая ошибка регулирования - отклонение регулируемой величины от заданного значения по окончании переходного процесса. 10. Динамическая ошибка регулирования - величина наибольшего отклонения регулируемого параметра от заданного значения (кроме начального отклонения). В системах автоматического управления возможны переходные процессы, характер протекания которых отличен от указанного на рисунок1. Все многообразие переходных процессов в системах автоматического управления можно разделить на три группы (рисунок.2): 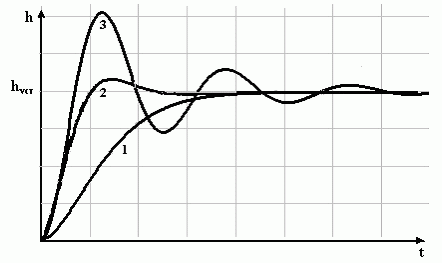 Рисунок2. Переходные процессы - монотонный процесс (1), когда скорость изменения управляемой величины (первая производная) не меняет знака в течение всего времени регулирования ( (dh/dt)≥0 при 0≤t≤tp); - апериодический процесс (2), когда скорость изменения управляемой величины меняет знак не более одного раза за время регулирования. - колебательный процесс (3), когда скорость изменения управляемой величины меняет знак периодически (более одного раза) за время регулирования. Связь показателей качества работы в замкнутой системе с ЛЧХ разомкнутой САУ. На рисунке.3 показаны типовые л.а.х. и л.ф.х. разомкнутой системы. Параметры переходного процесса (рисунок1) и ЛЧХ связаны между собой следующими соотношениями: 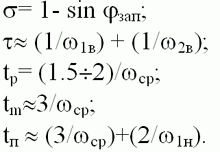 Из формул видно, что быстродействие САУ прямо пропорционально частоте среза ωcp, а колебательность обратно пропорциональна запасу устойчивости по фазе φзап. Следует отметить, что приведенные формулы являются приближенными (погрешность может составлять от 20 до 25 %), но на этапе предварительного анализа их использование может быть полезным. 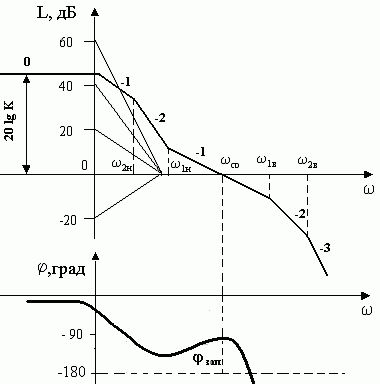 Рисунок 3. Типовые ЛЧХ разомкнутой САУ Методы повышения точности работы САУ Повышение точности работы САУ возможно с помощью изменения ее структуры или изменения параметров. Общими методами повышения точности являются: 1. Увеличение коэффициента усиления К разомкнутой системы (регулирование по отклонению с использованием П - регулятора). 2. Повышение порядка астатизма (регулирование по интегралу от ошибки с использованием ПИ - регулятора). 3. Применение регулирования по производным от ошибки ( с применением ПД - регуляторов). 4. Использование комбинированного управления. 5. Введение неединичных обратных связей. При регулировании по отклонению ошибка тем меньше, чем больше К. Метод эффективен, широко применяется, но в системах высокого порядка сказывается противоречие между требованием точности и требованием устойчивости. При увеличении К возрастает ωср и уменьшается запас устойчивости. |
