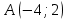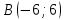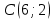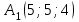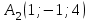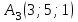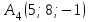рейтинговая работа математических и естественно-научных дисциплин. Рейтинговая работа №1. Кафедра математических и естественнонаучных дисциплин
 Скачать 181.55 Kb. Скачать 181.55 Kb.
|
 Кафедра математических и естественно-научных дисциплин Рейтинговая работа Контрольяная работа по дисциплине «Математика» Задание/вариант №7 Выполнена обучающимся группы Тепаевой Татяной Андреевной Преподаватель Сурина Елена Евгеньевна Москва – 2019 г. 1) Даны матрицы 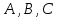 и число и число 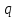 . Найти матрицу . Найти матрицу 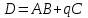 . .7). 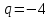 , , 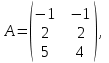 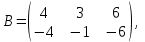 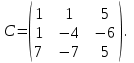 Решение: AB =  * * 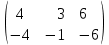 = число столбцов 1 матрицы (A) = числу строк 2 матрицы (B) = = = число столбцов 1 матрицы (A) = числу строк 2 матрицы (B) = =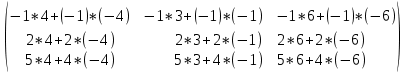 == ==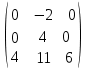 . .D = 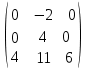 + + 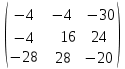 = = 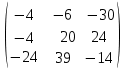 . .Ответ: D = 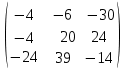 . .2) Дана система линейных алгебраических уравнений. Найти решение этой системы любым методом. 7). 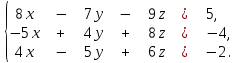 Решение: Для нахождения (x;y;z) используем метод Крамера Найдем определитель: 1 способ: Δ = 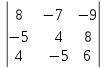 = 8 * = 8 *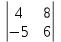 + 5 * + 5 *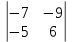 + 4 * + 4 *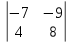 = = 8 * (24 + 40) + 5 * (–42 – 45) + 4 * (–56 + 36) = 8 * 64 + 5 * (–87) + 4 * * (–20) = 512 – 435 – 80 = –3 ≠ 0. = = 8 * (24 + 40) + 5 * (–42 – 45) + 4 * (–56 + 36) = 8 * 64 + 5 * (–87) + 4 * * (–20) = 512 – 435 – 80 = –3 ≠ 0.2 способ: Δ = 8 * 4 * 6 + (–5) * (–5) * (–9) + (–7) * 8 * 4 – 4 * 4 * (–9) – (–5) * 8 * * 8 – (–5) * (–7) * 6 = 192 – 225 – 224 + 144 + 320 – 210 = –3 ≠ 0. Данная система невыраженная. Δx = 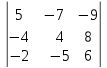 = 5 * = 5 *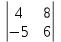 + 4 * + 4 *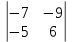 – 2 * – 2 *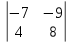 = = 5 * (24 + 40) + 4 * (–42 – 45) – 2 * (–56 + 36) = 5 * 64 + 4 * (–87) – 2 * * (–20) = 320 – 348 + 40 = 12; = = 5 * (24 + 40) + 4 * (–42 – 45) – 2 * (–56 + 36) = 5 * 64 + 4 * (–87) – 2 * * (–20) = 320 – 348 + 40 = 12;Δy = 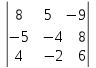 = 8 * = 8 *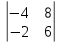 + 5 * + 5 *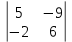 + 4 * + 4 *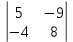 = = 8 * (–24 + 16) + 5 * (30 – 18) + 4 * (40 – 36) = –64 + 60 + 16 = 12; = = 8 * (–24 + 16) + 5 * (30 – 18) + 4 * (40 – 36) = –64 + 60 + 16 = 12;Δz = 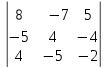 = 8 * = 8 *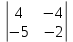 + 5 * + 5 *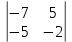 + 4 * + 4 *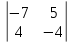 = = 8 * (–8 + 20) + 5 * (14 + 25) + 4 * (28 – 20) = –224 + 195 + 32 = 3. = = 8 * (–8 + 20) + 5 * (14 + 25) + 4 * (28 – 20) = –224 + 195 + 32 = 3.x = 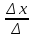 ; x = ; x = 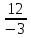 = –4; = –4;y = 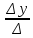 ; y = ; y = 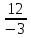 = –4; = –4;z = 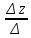 ; z = ; z = 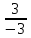 = –1. = –1.Ответ: (–4; –4; –1). 3) Известны координаты (см. таблицу 1) в прямоугольной системе координат 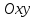 трех точек трех точек 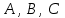 , являющихся вершинами треугольника. Изобразить треугольник , являющихся вершинами треугольника. Изобразить треугольник 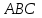 в этой прямоугольной системе координат и найти: в этой прямоугольной системе координат и найти:3.1 координаты векторов 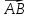 , , 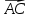 и их длины; и их длины;3.2 скалярное произведение векторов 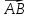 , , 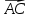 и угол и угол 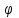 между векторами между векторами 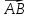 , , 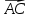 ; ;3.3 векторное произведение векторов 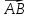 , , 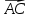 и площадь треугольника и площадь треугольника 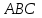 ; ;3.4 значение параметра 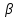 , при котором векторы , при котором векторы 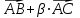 и и 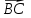 будут коллинеарны; будут коллинеарны;3.5 координаты точки 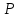 , делящей отрезок , делящей отрезок 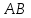 в отношении в отношении 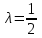 ; ;3.6 каноническое уравнение стороны 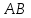 ; ;3.7 уравнение с угловым коэффициентом и угловой коэффициент прямой, проходящей через точку 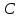 параллельно прямой параллельно прямой 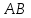 ; ;Таблица 1
Решение: Координаты точек A(-4;2); B(-6;6); C(6;2) – вершины ΔABC в прямоугольной системе координат. 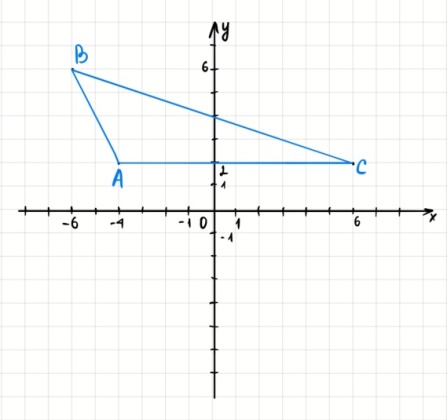 Изображение №1. ΔABC в прямоугольной системе координат. 3.1 координаты векторов 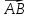 , , 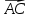 и их длины; и их длины;Решение: 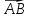 = {–6 – (–4); 6 – 2} = {–2; 4}; = {–6 – (–4); 6 – 2} = {–2; 4};| 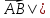 = { = { 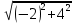 } = } = 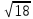 = 3 = 3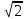 . .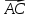 = {6 + 4; 2 – 2} = {10; 0}; = {6 + 4; 2 – 2} = {10; 0};| 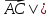 = { = { 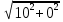 } = } = 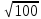 = 10. = 10.Ответ: 3 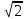 ; 10. ; 10.3.2 скалярное произведение векторов 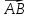 , , 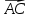 и угол и угол 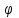 между векторами между векторами 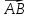 , , 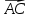 ; ;Решение: 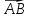 * * 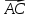 = | = |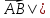 * | * |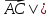 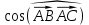 . .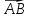 * * 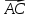 = –2 * 10 + 4 * 0 = –20; = –2 * 10 + 4 * 0 = –20;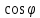 = = 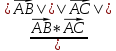 = = 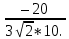 = = 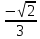 ; ;φ=arccos ( 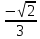 ) = π – arccos ) = π – arccos 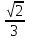 . .Ответ: π – arccos 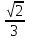 . .3.3 векторное произведение векторов 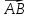 , , 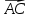 и площадь треугольника и площадь треугольника 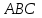 ; ;Решение: 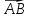 = {–2; 4}; = {–2; 4};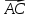 = {10; 0}; = {10; 0};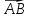 * * 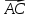 = | = |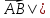 * | * |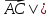 * * 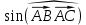 * * 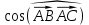 = = 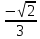 ; ;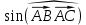 = = 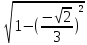 = = 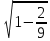 = = 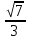 ; ;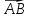 * * 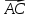 = 3 = 3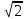 * 10 * * 10 * 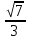 = 10 = 10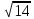 ; ;SΔABC = 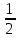 * * 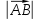 * * 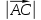 * * 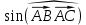 ; ;SΔABC = 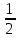 * 10 * 10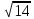 = 5 = 5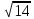 . .Ответ: 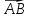 * * 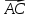 = 10 = 10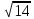 ; SΔABC = 5 ; SΔABC = 5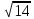 . .3.4 значение параметра 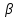 , при котором векторы , при котором векторы 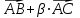 и и 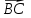 будут коллинеарны; будут коллинеарны;Решение: Если существует прямая, которой данные вектора параллельны, то эти вектора коллинеарны (координаты пропорциональны). 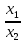 = = 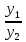 = k. = k.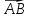 = {–2; 4}; = {–2; 4};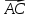 = {10; 0}; β = {10; 0}; β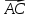 = {10β; 0}. = {10β; 0}.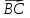 = {6 – (–6); 2 – 6} = {12; –4}. = {6 – (–6); 2 – 6} = {12; –4}.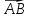 + β + β 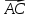 = {–2 + 10β; 4 + 0}. = {–2 + 10β; 4 + 0}.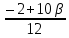 = = 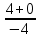 ; ;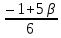 = –1; = –1;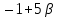 = –6; = –6;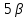 = –5; = –5;β = –1. Ответ: β = –1. 3.5 координаты точки 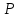 , делящей отрезок , делящей отрезок 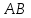 в отношении в отношении 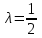 ; ;Решение: 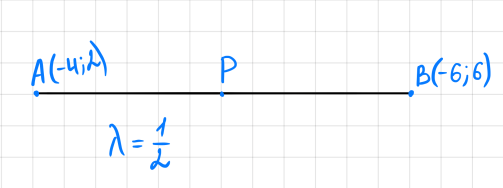 Изображение №2. Отрезок AB в отношении λ = 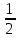 . .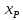 = = 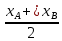 ; ; 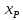 = = 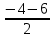 = –5. = –5.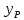 = = 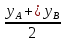 ; ; 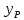 = = 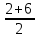 = 4. = 4.Ответ: P(–5; 4). 3.6 каноническое уравнение стороны 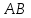 ; ;Решение: A(-4;2); B(-6;6). 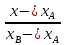 = = 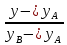 ; ;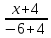 = = 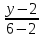 ; ;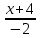 = = 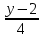 ; ;4x + 16 = –2y + 4; 2y + 4x + 12 = 0; y + 2x + 6 = 0; k = –2. Ответ: k = –2. 3.7 уравнение с угловым коэффициентом и угловой коэффициент прямой, проходящей через точку 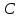 параллельно прямой параллельно прямой 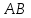 ; ;Решение: Уравнение прямой проходящей через точку C параллельно прямой AB (коэффициенты параллельных прямых равны). Уравнение с прямой AB: y + 2x + 6 = 0; y = –2y – 6; k = –2. Уравнение прямой, проходящей через точку C: y = –2y + 6. Ответ: y = –2y + 6. 4) Известны координаты (см. таблицу 2) в прямоугольной системе координат 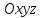 вершин пирамиды вершин пирамиды 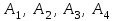 . .4.1 найти смешанное произведение векторов 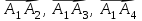 и объем пирамиды и объем пирамиды 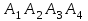 ; ;4.2 найти каноническое уравнение прямой 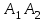 ; ;4.3 найти общее уравнение плоскости 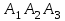 ; ;Таблица 2
Решение: 4.1найти смешанное произведение векторов 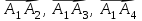 и объем пирамиды и объем пирамиды 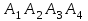 ; ;Решение: Координаты векторов 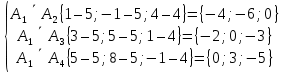 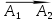 * ( * (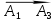 * * 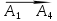 ) = ) = 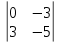 * (–4) – * (–4) – 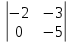 * (–6) + + * (–6) + + 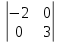 * 0 = (0 + 9) * (–4) – 10 * (–6) + (–6) * 0 = –36 + 60 + 0 = 24; * 0 = (0 + 9) * (–4) – 10 * (–6) + (–6) * 0 = –36 + 60 + 0 = 24;Vпир. = 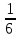 * 24 = 4. * 24 = 4.Ответ: 24; Vпир. = 4. 4.2 найти каноническое уравнение прямой 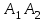 ; ;Решение: Пусть A1(5; 5; 4), а A2(1; –1; 4) Пусть 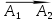 { {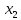 – – 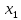 ; ; 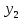 – – 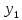 ; ; 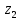 – – 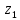 } = {1 – 5; –1 – 5; 4 – 4} = {–4; –6; 0} – направляющий вектор прямой } = {1 – 5; –1 – 5; 4 – 4} = {–4; –6; 0} – направляющий вектор прямой 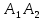 . .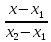 = = 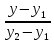 = = 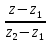 или или 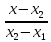 = = 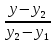 = = 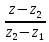 т.е. т.е. 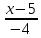 = = 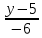 = = 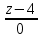 или или 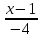 = = 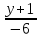 = = 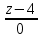 . .Ответ: 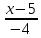 = = 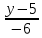 = = 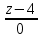 или или 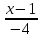 = = 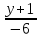 = = 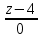 . .4.3 найти общее уравнение плоскости 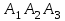 ; ;Пусть A1(5; 5; 4), A2(1; –1; 4), A3(3; 5; 1). Уравнение прямой, проходящая через три точки записывается в таком виде: 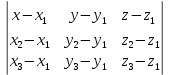 = = 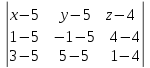 = = = = 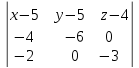 = 18 * (x – 5) + 0 * (y – 5) + 0 * (z – 4) – (12 * (z – 4) + + 0 * (x – 5) + 12 * (y – 5)) = 18 * (x – 5) + 12 * (z – 4) + 12 * (y – 5) = 18x – 90 – 12z + 48 – 12y + 60 = 18x – 12y – 12z + 18. = 18 * (x – 5) + 0 * (y – 5) + 0 * (z – 4) – (12 * (z – 4) + + 0 * (x – 5) + 12 * (y – 5)) = 18 * (x – 5) + 12 * (z – 4) + 12 * (y – 5) = 18x – 90 – 12z + 48 – 12y + 60 = 18x – 12y – 12z + 18.Следовательно, 18x – 12y – 12z + 18 = 0. Ответ: 18x – 12y – 12z + 18 = 0. | ||||||||||||||||||