Термех. термех. 1 Векторное исчисление Вектор и его модуль

• Название: 1 Векторное исчисление Вектор и его модуль
• Анкор: Термех
• Дата: 09.03.2023
• Размер: 2.59 Mb.
• Имя файла: термех.docx
• Тип: Документы; #976014
• страница: 1 из 6

(1)Векторное исчисление

1.Вектор и его модуль.

Вектор-есть направленный отрезок. Произвольные вектора

обозначим . Всякая формула, в которой встречаются такие векторы, справедлива для любого вектора. На рисунках вектор изображается в виде стрелки. Он характеризуется длиной отрезка и его направлением.Длина вектора, изменяемая в выбранной системе единиц, называется Модулем вектора и обозначается =Ю

2.Проекция вектора и знаки проекций.

Выберем некоторое неподвижное начало отчета 0 и введем декартовую систему координат с осями ох,оy,oz. Отложим произвольный вектор из начала координат.Определим проекции вектора на оси координат как длины отрезков, отсекаемых перпендикулярами, опущенными на эти оси. Их будем обозначать Ю_х ,Ю_у ,Ю_z.

Модуль вектора через его проекции выражается по т. Пифагора формулой



Проекция вектора на ось считается положительной, если координата конца вектора больше координаты его начала. Вектор не зависит ни от системы координат,след-но и ни он его модуля , направление также не зависит от системы отсчета. Это св-во векторов называется инвариантностью(независимостью) вектора относительно преобразования системы координат


3.Умножение вектора на скаляр.

В результате умножения вектора на скаляр λ получим вектор = λ , Направление которого при положительных значениях λ совпадает с направлением вектора . Если λ<0, то вектор имеет противоположное направление. Модуль вектора зависит от λ и определяется формулой Э= λЮ если <1,то вектор будет короче вектора Ю,если больше 1,то происходит растяжение векторa.Проекции векторов Э и Я связаны соотношениям Эх = λЮх, Эу = λЮу, Эz = λЮz

4.Составляющие вектора

Если вектор имеет модуль, равный единице,то он называется единичным вектором. Модули единичных векторов являются безразмерными величинами ,а их направления совпадают с направлением координатных осей. Такие векторы наз-ся единичными векторами координатных осей, или ортами осей.В декартовой системе отры принято обозначать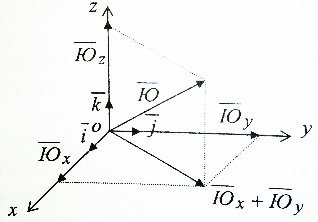



Составляющая вектора вдоль коорд-ой оси ox называется вектор =Ю_x , для осей 0y и 0z =Юy , =Ю_z (произведение единичного вектора оси и проекции вектора на эту ось.) Любой вектор можно разложить на три составляющие вдоль координатных осей. = _x + _y + _z =Юx +Юy +Юz

5.Правые и левые системы координат.

В математических расчетах используются так называемые правые и левые системы декартовых координат,которые отличаются взаимным расположением координатных осей.Правило правого винта(для правых систем координат) Вначале отложим сомножители из одной точки. Далее совместим плоскость головки винта с плоскостью векторов Ю(ox) и Я(oy), и правой рукой будем завинчивать винт с правой резьбой по кратчайшему расстоянию от первого сомножителя ко второму. Направление завинчивания совпадает с направлением вектора Э(oz). В левых системах координат вводится правило левого винта. Всякое вращение против хода часовой стрелки в теоретической механике считается положительным.



6.Векторное произведение двух векторов.

В результате векторного умножения двух векторов получается векторЭ=ЮхЯ , определяемый двумя способами – аналитическим и геометрическим.

При аналитическом способе вектор Э находится по проекциям на оси координат согласно формулам:

Эx =ЮyЯz -ЮzЯy , Эy =ЮzЯx -ЮxЯz , Эz =ЮxЯy -ЮyЯx.



При геометрическом способе вектор Э строится перпендикулярно плоскости, проведенной через сомножители Ю иЯв соответствии с правилом правого винта Его модуль вычисляется по формуле Э=ЮЯ sina. Здесь a- угол между векторами Ю и Я .

7.Скалярное произведение двух векторов.

В результате скалярного умножения двух векторов получается скаляр Э=Ю Я , определяемый двумя способами: а) Э=Юx Я x +Юy Я y +Юz Я z. б) Э=ЮЯ cosa.

Здесь a- угол между векторами Ю и Я .

8. Переменный вектор.

Если записано Ю=Ю(t), то это означает, что с изменением параметра t меняется или модуль, или направление вектора , или - и то и другое. В общем случае Ю=Ю(t), Юx =Юx(t), Юy =Юy(t), Юz =Юz(t). Годографом вектора называется линия, которую вычертит конец вектора при плавном изменении t , если вектор откладывать из неподвижного начала отсчета.




9.Производная от вектора.

Пусть ∆ t0) есть приращение вектора при изменении аргумента на величину ∆t=t-t0.Вектор производной обозначается и определяется соотношением Вектор направлен по касательной к годографу вектора и вычисляется согласно формуле


Последняя формула получена после дифференцирования = _x + _y + _z =Юx +Юy +Юz . по аргументу t и тогда с использованием формулы получаем

т.к. векторы ijk орты неподвижной системы координат и поэтому постоянны и в результате имеем формулу(*)

(2)Векторный способ задания закона движения точки
1.Радиус-вектором и траектория движущейся точки



(рассмотрим неподвижную систему отсчета с центром о и движущуюся точку b) Радиус-вектором точкиbназывается вектор , исходящий из начала отсчета “о”, конец которого находится в точке b. Закон движения определяется соотношением = (t). Траектория точкиb есть годограф радиус-вектора.


2.Определение скорости точки.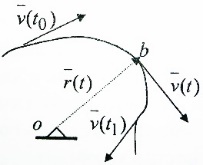



Скорость точки b будем называть вектор определенной формулой (производная по времени от радиус вектора) Вектор скорости направлен по касательной к траектории движущейся точки.

Проинтегрировав обе части формулы получим закон движения точки:


3.Определение ускорения точки



Ускорением движущейся точки b назовем вектор ,определенной формулой

Вектор будет направлен по касательной к этому годографу

Проинтегрировав обе части по времени формулы получим:

Отсюда следует, что:

(3)Координатный способ задания закона движения точки

1.Закон движения и траектория точки

Закон движенияопределяется соотношениями:x_b= x(t), y_b= y(t), z_b= z(t).

Здесь x(t), y(t), z(t) -координаты движущейся точки b…x_b,y_b,z_b-координаты точки b определяющиеся длиной соответствующих отрезков на осях координат. Для определения уравнения траектории в явном виде надо из закона движения исключить время t . ..В случае когда точка b движется в плоскости oxy,для определения закона движения достаточно задать две ее координаты x_b=x(t), y_b=y(t) исключив из них время t, получим одно соотношение F(x,y)=0,которое и является уравнением траектории точки.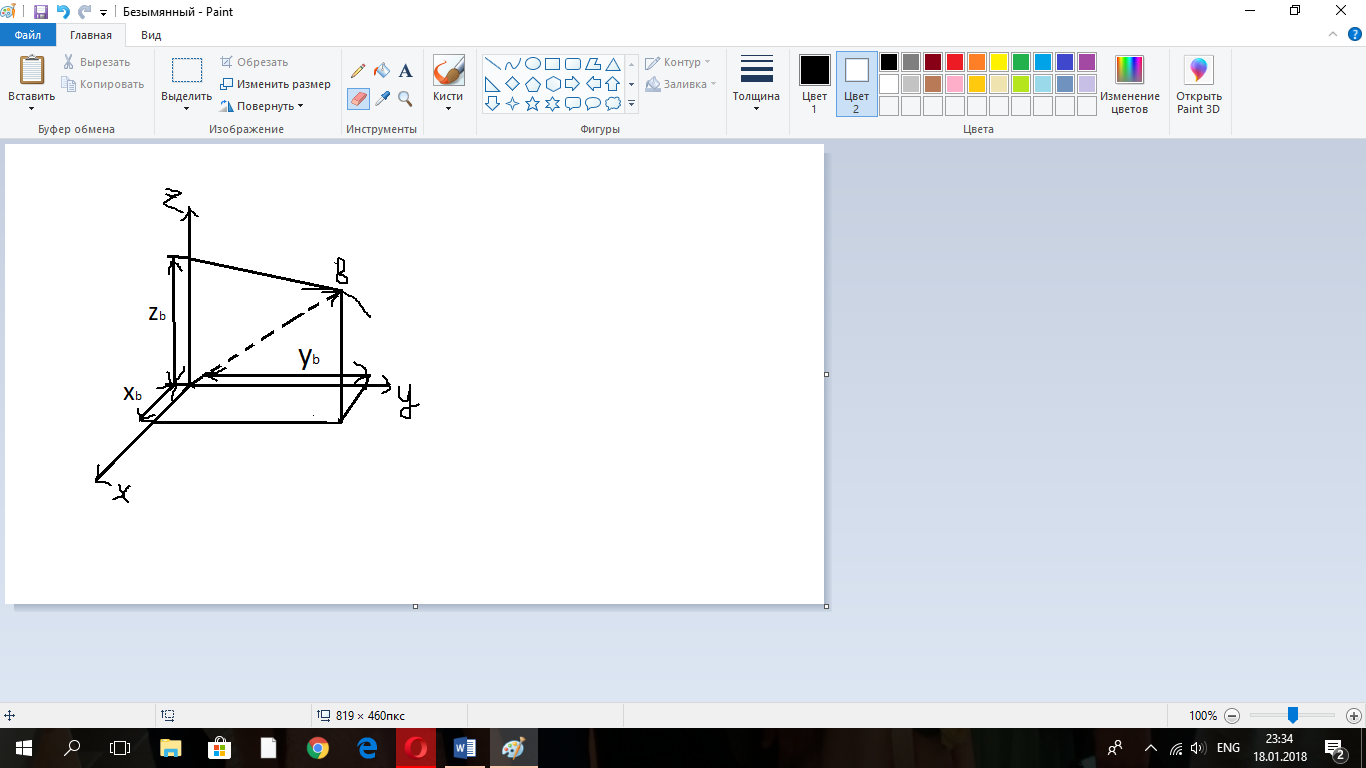

2.Определение скорости и ускорения точки

Задание закона движения позволяет вычислить вектор скорости движущейся точки аналитическим способом т е по проекциям на оси координат.следует проекция радиус вектора на оси координат равны координатам точки b т е r_x=x_b,r_y=y_b,r_z=z_bследует. =x_b +y_b +z_b Производная от радиус вектора равна вектору скорости точки.следуетv_x= , v_y= ,v_z= .. вектор скорости и его модуль при этом определяется формулами =v_x +v_y +v_z , v= Аналогично найдем вектор ускорения точки b продиф-ем по времени и получим w_x= , w_y= ,w_z= вектор ускорения и его модуль представим в виде =w_x +w_y +w_z , w=

(4)Естественный способ задания закона движения точки.

1.Естественная система координат.

Пусть т.b движется по известной траектории. При этом говорится ,что точкадвижется по прямой , окружности и т.д. На траектории выбирается некоторая фиксированная т. и задается длина дуги s, отсекаемая т.b, как ф-ия времени.Кроме этого, указывается положительное направление отсчета длины дуги.Если ф-ия s = s(t) известна, то вычислив ее значение,в любой момент времени может определить положение т.b в пространстве. Следовательно , s = s(t) задан закон движения т. , и способ задания в этом случае наз-ся естественным.



Определим естественную систему координат. Ее начало отсчета поместим в движущуюся т. b. Первую ось с ортом направим по касательной к траектории в сторону положительных дуг s(t). Вторую ось свяжем с направлением главной нормали и месте с ортом направим в сторону вогyтости траектории т. b. Если траектория- прямая, то вектор перпeндикумpeн этой пpямой. Третью ось с единичным вектором направим перпендикулярно первым двум по бинормали к траектории. При этом орты связаны соотношением =

Единичные векторы выполняют роль ортов i, j,k декартовой сис- темы координат, однако принципиально отличаются от последних. При движении т. b касательная и нормали к траектории в общем случае могут поворачиваться. Поэтому с течением времени орты , оставаясь по модулю равными единице, могут изменять свое направление. Следовательно, в отличие от постоянных векторов i, j,k, имеем: = (t), = (t), = (t)

2.Определение скорости и ускорения точки.

Пусть закон движения точки b задан естественным способом в форме (s = s(t)). Ее радиус-вектор будем считать сложной функцией времени, полагая, что вначале зависит от длины дуги s,а потом от времени t. Итак, = [s(t)]. Продифференцируем по времени последнее равенство. =d /ds* ds/dt производная от радиус-вектора движущейся точки по длине дуги равна единичному вектору касательной к траектории d след-но =



Мех. Смысл производной v_τ= –проекция вектора скорости на направление касательной к траектории

Вектор ускорения раскладывается на две составляющие, параллельной касательной и главной нормали к траектории точки , Модуль вектора ускорения w=



\

(5)Поступательное движение твердого тела.
Движение тела называется поступательным, если любая прямая, проведенная в теле, движется параллельно самой себе.

Доска движется не прямолинейно, но поступательно.