Термех. термех. 1 Векторное исчисление Вектор и его модуль

• Название: 1 Векторное исчисление Вектор и его модуль
• Анкор: Термех
• Дата: 09.03.2023
• Размер: 2.59 Mb.
• Имя файла: термех.docx
• Тип: Документы; #976014
• страница: 5 из 6

3.Уравнение равновесия сходящейся системы сил.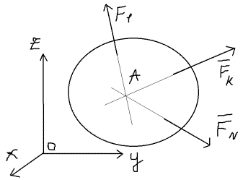


Главный момент внешних сил , вычисленный относительно А равен нулю, поскольку ни одна сила не создаёт момента относительно этой точки. Если Главный вектор внешних сил равен нулю, то главный момент , вычисленный относительно любой точки о, будет тождественно равен нулю.
Для равновесия сходящейся системы сил необходимо и достаточно, чтобы суммы проекций всех сил на оси координат были равны нулю.
,


4.Уравнения равновесия плоской системы сил.
Система сил, действующих на твердое тело, называется плоской, если все силы находятся в некоторой неподвижной плоскости oxy .
Уравнения равновесия плоской системы сил можно записать в трех следующих формах:
Здесь точка “o” –любая точка плоскости oxy .
,
Здесь ось ox не должна быть перпендикулярна прямой оА.
Здесь точки о,А,В не должны лежать на одной прямой.


(22)Допустимые преобразования системы внешних сил, действующих на твёрдое тело.
1.Эквивалентные системы внешних сил и допустимые преобразования.
Две системы внешних сил F1,F2,..,F N и G1,G2,..,Gs называются эквивалентными, если при замене одной системы сил на другую состояние движения тела (покой) не изменится. Эквивалентные системы сил имеют одинаковые главный вектор и главный момент. Преобразования системы внешних сил, действующих на твердое тело, называются допустимыми, если они не меняют главного вектора и главного момента.

2.Элементарные примеры допустимых преобразований.
1.Сила, действующая на твёрдое тело, есть вектор скользящий.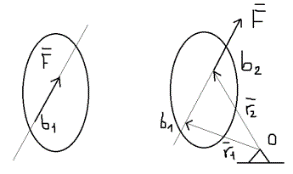

Пусть сила приложена к точке b_1. Если мы приложим её в точке b₂, лежащей на линии действия, то первая из сумм не изменится. Это очевидно, так как силу мы не изменяли по модулю и не поворачивали.
Сравним моменты силы , приложенной в точках b₁ и b₂. Обозначим: –
Следовательно, при сдвиге силы вдоль линии действия её момент не изменится и вместе с ним не изменится вторая сумма. Итак, преобразование допустимо.
2.Две силы, приложенные в одной точке тела, можно заменить их геометрической суммой.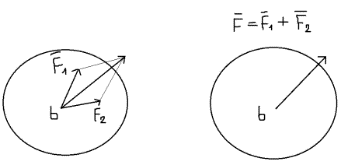

Пусть в некоторой точке приложено две силы: При замене двух сил одной силой первая из сумм не изменится. На основании теоремы о моменте суммы имеем:
. Поэтому не изменится и главный момент. Преобразование допустимо.
Силу, действующую на твёрдое тело, можно разложить на любое число составляющих.


3.Центр тяжести твёрдого тела.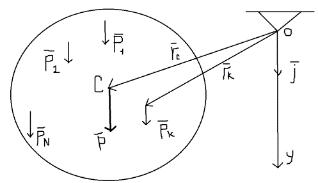

Систему сил тяжести точек твердого тела можно заменить одной силой , приложенной в центре тяжести C.
Положение центра тяжести определяется формулами , , .
Здесь -радиус-вектор и координаты точки С. Центр тяжести тела совпадает с центром масс тела.

4.Распределённые нагрузки.
Пусть - удельный вес тела. Вес произвольной бесконечно малой точки b тела обозначим dp, а её объём – dV. Тогда и суммы бесконечно малых величин представим интегралами в виде .
При выполнении этих условий замена системы сил тяжести одной силой становится допустимой и из неё следует определить точку приложения силы . Здесь
Аналогом удельного веса в распределённых нагрузках является величина q, которая называется интенсивностью распределённой нагрузки. Если q=const, то нагрузка называется равномерно распределённой.
- для нагрузок, распределённых по объёму V, ;
-для нагрузок, распределённых по площади S, ;
-для нагрузок, распределённых по линии длиной L, .
Здесь - радиус-вектор точки приложения равнодействующей силы . Направление этой силы должно совпадать с направлением нагрузки.
Равнодействующая равномерно распределённой нагрузки прикладывается в центре тяжести соответствующего геометрического объекта – объёма, площади или линии.
Равномерно распределенную нагрузку интенсивности q, приложенную на прямолинейном участке тела длиной L, можно заменить равнодействующей силой Q =qL , приложенной в середине участка.
(23)Пара сил. 1.Момент пары.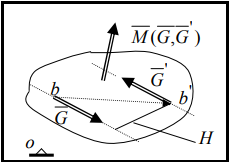

Парой сил называется система двух сил ( , равных по величине и противоположно направленных, т.е. .
Моментом пары сил ( 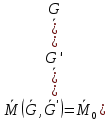называется вектор , равный сумме моментов сил, составляющих пару (при этом моменты могут вычисляться относительно любой точки). .
Плечом пары сил называется расстояние H между линиями действия сил . Модуль момента пары равен произведению модуля одной из сил и плеча пары, т.е. M =GH. В плоском случае момент пары сил определяется как скалярная величина по формуле M =±GH. Знак “+” следует ставить, если пара сил вращает свое плечо против хода часовой стрелки. Действие пары сил на тело полностью характеризуется моментом пары.

2.Допустимые преобразования пары сил.
Допустимыми будут такие преобразования пары, которые не изменяют её момента.
I. Как жесткое целое пару сил ( можно сдвинуть произвольным образом и перенести в любое место тела при условии сохранения направления вектора .
II. Силы можно сдвинуть вдоль линий их действия.
III. Можно уменьшить модули сил и пропорционально увеличить плечо пары H (сохранив произведение GH).
IV. Если на тело действует несколько пар сил ( с моментами , то их можно заменить одной парой ( с моментом

(24)Теорема Пуансо.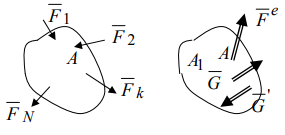

Рассмотрим произвольную систему сил действующих на абсолютно твёрдое тело. Выберем в теле произвольную т.А, назовём её центром приведения, а дальнейшую процедуру назовём приведением исходной системы сил к заданному центру.
Все силы, приложенные к т. на основании леммы о параллельном переносе сил, не меняя их направления и модуля, перенесём в точку А, но при этом к телу доп. след. приложить присоед. пары. Моменты этих пар равны моментам сил исходной системы, выч. относительно центра приведения. .
На основании аксиомы о сложении сил, приложенных к одной точке, сложим все силы, приложенные к точке А и заменим их одной силой. На основании теоремы о сложении пар сист. присоед. Пар можем заменить одной парой сил ( , момент которой равен сумме моментов исходной системы сил, вычисленных относительно центра приведения т.е.
Формулировка: Произвольную систему внешних сил , действующих на твердое тело, можно заменить тремя силами , первая из которых равна главному вектору и приложена в центре приведения A .Две другие силы образуют пару ( , момент которой равен главному моменту исходной системы сил относительно центра приведения.

(25)Заделка. Неподвижный шарнир. Подвижная опора. Реакции в них.
Заделка. В строительстве заделка реализуется, когда балка забетонирована в стену, в технике заделка реализуется, когда стальной стержень приварен к массивному телу.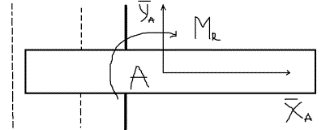

В результате ограничения поворота в заделке дополнительно появляется пара реактивных сил , момент которой называется реактивным моментом.
Действие жёсткой заделки на твёрдое тело в силовом отношении сводится к реакции , которую обычно разлагают на две составляющие и , и паре сил с моментом Таким образом, в заделке следует определять три неизвестные величины – модули составляющих реакции и реактивный момент. Пара сил в заделке обычно не изображается, но указывается её момент
Иногда для крепления тел используется скользящая заделка. От жёсткой она отличается тем, что тело имеет возможность свободно двигаться в некотором направлении. Действие скользящей заделки на тело сводится к одной силе с известным направлением и паре сил с моментом В этом случае требуется определить только две неизвестные величины.
Подвижные опоры.
Такие опоры могут содержать некоторые подвижные элементы, которые имеют возможность прямолинейно перемещаться, либо включают в себя два цилиндрических шарнира.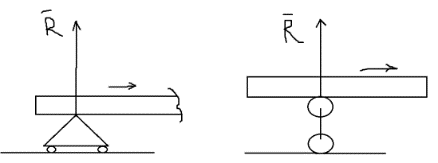

Конструктивно подвижные опоры весьма различны. Особенностью связей, которые подвижные опоры накладывают на тело, является возможность для тела иметь свободное перемещение в каком-либо направлении. Это определяет отсутствие составляющей реакции данного направления. Реакция подвижной опоры направлена перпендикулярно тому направлению, в котором опора не мешает двигаться телу. Здесь мы имеем одну неизвестную величину – модуль R опорной реакции.
Шарнирные крепления.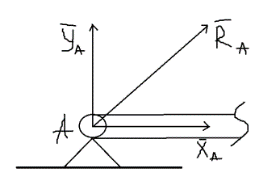

В качестве примера шарнирного крепления можно привести дверные и оконные петли. Механическая суть его заключается в том, что точка А тела, непосредственно контактирующая с осью шарнира, неподвижна. Само же тело может свободно вращаться вокруг этой оси.
В неподвижном шарнире отсутствует ограничение на поворот балки вокруг т.А, поэтому реактивная пара сил в шарнире отсутствует и система реактивных сил, действующих на балку со стороны шарнира эквивалентна только одной силе. Обычно её разлагают на 2 составляющие вдоль координатных осей. В неподвижном цилиндрическом шарнире имеется 2 неизвестные величины , которые следует определять из уравнения равновесия.

(26)Работа силы.

1.Дифференциал вектора.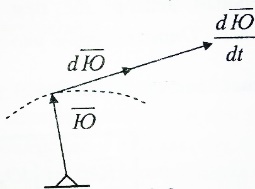



Дифференциалом вектора функции (t) будем называть вектор d определенный соотношением d = dt.

Вектор d получается умножением вектора производной на положительный скаляр dt.

2)Вектор бесконечно-малого пути.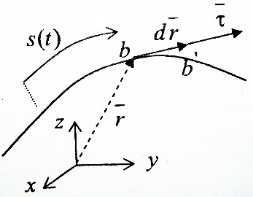



Рассмотрим движение точки b за бесконечно-малое время dt из положения «b» в положение «b`». bb`=dS – бесконечно-малый путь, пройденный точкой b за время dt.

= | dt



Длина вектора .

Согласно (*) вектор направлен по касательной к траектории. Отсюда следует, что вектор можно рассматривать как вектор бесконечно-малого пути, пройденный точкой за время dt.

| dt



В результате имеем вектор бесконечно-малого пути имеет проекции на оси коорд. равные дифференциалам координат в точке b







Так как - вектор бесконечно-малого пути, то часто пишут


3)Элементарная работа силы.

Пусть точка b под действием силы F за время dt из положения b перешла в положение b`.

Определение: элементарная работа силы F (т.е. работы на бесконечно-малом пути bb`) будем называть скаляр, обозначаемый d`A и определяемый формулой d`A = 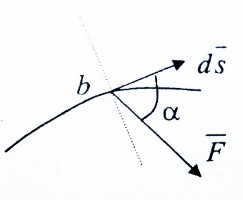. Здесь штрих стоит для того, чтобы элементарную работу в общем случае не считать полным дифференциалом.



Имеем

Пусть 0 < α < 90 следовательно cosα> 0, d`A> 0. «Разгоняющая» сила имеет «+» элементарную работу.

Пустьα=90, cos90=0, d`A=0

Если сила перпендикулярна траектории, то ее элементарная работа равна нулю.

Пусть 90 < α < 270, cosα < 0, d`A < 0

Элементарная работа «тормозящей» силы отрицательна.

d`A = .

4) Работа силы на конечном перемещении.

Пусть точка b под действием F движется от положения 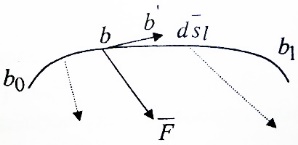до положения



Разделим дугу 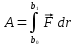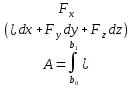на множество бесконечно-малых участков bb` и пронумеруем их. Просуммируем элементарные работы силы F на всех бесконечно-малых участках A =






5)Работа равнодействующей силы.

Пусть в движущейся точке приложено несколько сил 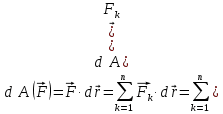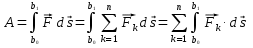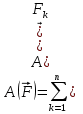с равнодействующей , тогда элементарная работа силы F может быть представлена:







(27)Частные случаи вычисления работы

1)Работа силы, направленной по нормали к траектории.

Примером нормальной силы является натяжение веревки, на котором качается шарик.



d всегда

d`A = 0

работа нормальной силы всегда равна нулю.


2) Работа постоянной силы.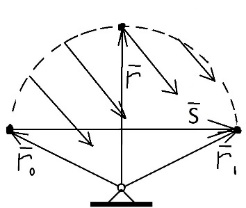



Пусть 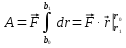=const

= F( )

Введём вектор =

будем называть вектором кротчайшего расстояния между и

А(

Работа постоянной силы равна скалярному произведению вектора силы и ректора кратчайшего расстояния.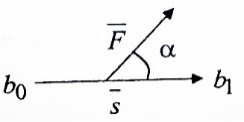



Если точка движется по прямой, то тогда А = FScosα

Формула верна. когда F=const и точка движется по прямой.


3) Работы упругой силы пружины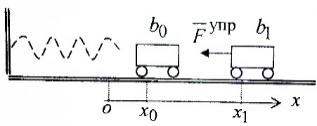



длина ненапряженной пружины, здесь F- сила упругости пружины, её проекция на ось x : , здесь С- коэфф. жесткости пружины.

y=z=0

d’A= -cxdx

Пусть тележка сдвинулась из положения в положение , тогда

A=


4) Работа силы тяжести материальной точки.

Пусть в точке b движется под действием силы P от положения 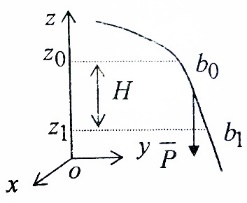до .



Введём вертикальную ось oz.

Px=Py=0

Pz=-P

d’A=-Pdz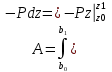



A=P( = , h-перемещение точки по высоте.

Работа силы тяжести точки равна взятому с соответствующим знаком произведения модуля веса и перемещения точки по высоте.

5)Работа силы тяжести точек твёрдого тела.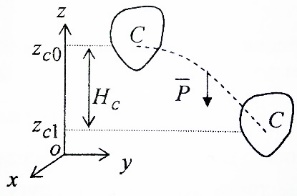



Определим сумму работ сил тяжести 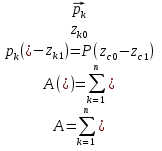, в случае произвольного движения твёрдого тела.



= – высота перемещения центра тяжести.

A= – работа положительна при движении точки C вниз.

6)Работа вращающего момента.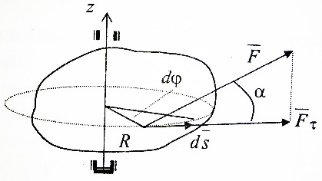



За бесконечно малое время dt точка b перейдет в положение b’, вектор бесконечно малого пути dS направлен по касательной к траектории.

Работа на бесконечно малом пути dS

– проекция F на касательную к траектории.

dS=bb’=Rdφ

– момент силы F относительно оси z.

d’A= dφ

d’A=

Сравнивая эти две формулы, говорят что сила работает на перемещении, а момент на угле поворота.

Рассмотрим конечное положение точки b от 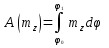до .



Пусть , тогда A= следовательно A= , где .

Работа постоянного вращательного момента равна произведению вращательного момента и угла поворота тела.


7)Работа внутренних сил в твёрдом теле.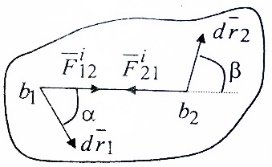



Рассмотрим бесконечно малое перемещение за время dt абсолютно твёрдого тела. Выберем в теле две взаимодействующие точки и . Точка получит перемещение , точка сместится на . Пусть точка действует на точку с силой , а с силой , то по 3-му закону Ньютона . Запишем сумму элементарных работ этих двух сил d’A ) + d’A( = + = (

Так как тело абсолютно твёрдое, то расстояние между точками 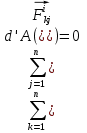и при движении не должно меняться и скобка в последнем уравнении должна быть равна 0.



– это равнодействующая всех внутренних сил, действующих на произвольную точку .

По теореме о работе равнодействующей : .

Проинтегрировав элементарные работы всех внутренних сил на соответствующие перемещения получим




(28)Кинетическая энергия.
1.Общие определения.

Рассмотрим движение отдельной материальной точки. Пусть точка b движется со скоростью . Выражение кинетической энергии материальной точки можем представить в двух формах:

. Кинетическая энергия материальной точки равна половине массы точки и квадрат модуля её скорости.

Пусть движется произвольная механическая система. Кинетическая энергия механической системы – сумма кинетических энергий всех её точек.

.


2.Кинетическая энергия твёрдого тела при поступательном движении.



Рассмотрим поступательное движение твёрдого тела, когда его центр тяжести движется со скоростью .

, – масса тела.

. При поступательном движении твёрдого тела, его кинетическая энергия равна половине произведения массы тела и квадрата скорости его центра тяжести.


3.Кинетическая энергия твёрдого тела при вращении вокруг неподвижной оси.



Выразим модуль вектора скорости произвольной точки тела через угловую скорость :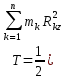

, – расстояние от точки до оси вращения. Тогда ) ,

– момент инерции тела относительно оси вращения.



Кинетическая энергия тела при вращении вокруг неподвижной оси равна половине произведения момента инерции тела ( относительно оси вращения ) и квадрату угловой скорости.

4.Кинетическая энергия тела при плоском движении.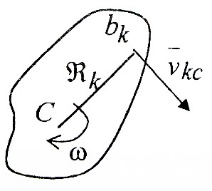



По формуле разложения плоского движения тела на две составляющие, где в качестве полюса примем центр тяжести, тогда , где - скорость, когда точка имеет только во вращении вокруг центра тяжести.

, - расстояние от произвольной точки до полюса.

, где – количество движения тела, которое оно имеет при неподвижном центре тяжести за счет вращения вокруг него.

, здесь введено обозначение , – момент инерции тела относительно оси c , проходящей через центр тяжести перпендикулярно плоскости движения тела.

Полученное выражение кинетической энергии отражает наличие двух составляющих плоского движения. Первое слагаемое в формуле соответствует поступательной части движения, а второе вращению тела вокруг центра тяжести.

В случае свободного движения , где – момент инерции тела относительно мгновенной оси вращения.

(29)Теорема об изменении кинетической энергии материальной точки.

Рассмотрим движение материальной точки под действием системы сил с равнодействующей .

По основному уравнению динамики после скалярного умножения правой и левой части соотношения на дифференциал радиус вектора точки b, тогда с учетом равенства получим : m .

Правая часть равенства представляет собой элементарную работу равнодействующей : d’A(



Теорема об изменении кинетической энергии материальной точки в дифференциальной форме :



Дифференциал кинетической энергии материальной точки равен элементарной работе равнодействующей всех сил, действующих на точку.

Рассмотрим конечное перемещение точки от положения 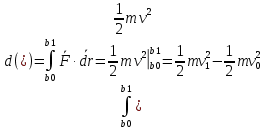до положения , просуммировав получим :

.

Интегральная форма теоремы об изменении кинетической энергии материальной точки :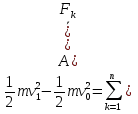

Изменение кинетической энергии материальной точки при некотором её перемещении равна сумме работ всех сил, действующих на точку ( на этом перемещении ).

Теорема об изменении кинетической энергии механической системы и твёрдого тела.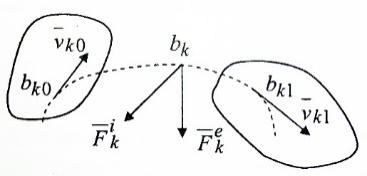



Рассмотрим движение произвольной механической системы. К точке приложены внешние и внутренние силы с равнодействующими , . Под действием этих сил точка перемещается с положения в положение , скорость точки в этих положениях обозначим соответственно и .

Запишем теорему об изменении кинетической энергии для каждой точки .

( )

Просуммировав получим

Введём обозначения : , ,



Изменение кинетической энергии произвольной механической системы при некотором её перемещении равно сумме работ всех внешних и внутренних сил в системе на соответствующих перемещениях отдельных точек системы.

В случае абсолютно твёрдого тела формула примет вид :


(1)Векторное исчисление

1.Вектор и его модуль.

2.Проекция вектора и знаки проекций.

3.Умножение вектора на скаляр.

4.Составляющие вектора

5.Правые и левые системы координат.

6.Векторное произведение двух векторов.

7.Скалярное произведение двух векторов.

8.Переменный вектор.

9.Производная от вектора.

(10)Векторный способ задания закона движения точки

11.Радиус-вектор и траектория движущейся точки