Термех. термех. 1 Векторное исчисление Вектор и его модуль
 Скачать 2.59 Mb.
|
|
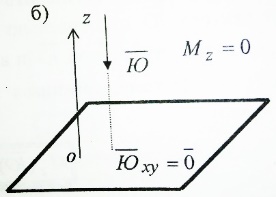1) вектор  OZ.   момента нет. 2) линия действия вектора 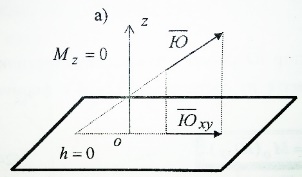 OZ. Оба этих случая объединяет тезис. Вектор  не создает «вращения» вокруг оси OZ.  Вывод: момент относительно точки есть характеристика вращения вокруг точки. Момент относительно оси есть характеристика вращения вокруг оси. Если вращения нет, то моменты равны нулю. (18)Теорема об изменении кинетического момента. 1.Момент силы. 2.Момент количества движения материальной точки. Рассмотрим движение мат. Точки под действием силы 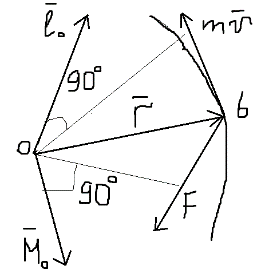 , которую в общем случае будем понимать как равнодействующую всех сил, действующих на точку, т.е.  . Количество движения точки  . Момент вектора количества движения  будем обозначать  .Имеем:  Если ввести систему декартовых координат с центром в точке о и проектировать формулы (1) и (2) на оси ox, oy, oz, то получим выражения моментов силы и моментов количества движения относительно координатных осей:  ,   3.Теорема об изменении момента количества движения материальной точки. Вывод теоремы начнём с основного уравнения термодинамики, записанного для точки b в виде  . Умножим это соотношение векторно слева на радиус-вектор точки, в результате имеем:  Справа получили известную величину – момент вектора силы отн. т. О. Для исследования левой части проведём следующее преобразование:  .В результате получим  (1) Теорема: Производная по времени от момента количества движения материальной точки равна моменту равнодействующей всех сил, действующих на точку. Скалярный аналог получим, спроектировав (1) на оси к-т.  4.Кинетический момент механической системы. 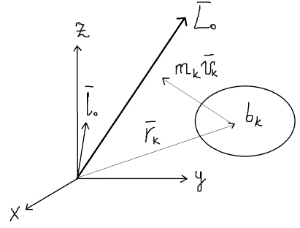 Кинетическим моментом механической системы относительно центра о называется сумма моментов количества движения всех её точек(вычисленных отн. того же центра). Итак,  .Вектор  момент количеств движения механической системы.Спроектируем на оси :  Введённые величины называются кинетическими моментами механической системы отн-но координатных осей.5.Второе свойство внутренних сил в механической системе. 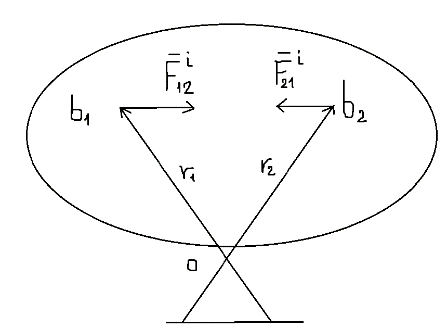 Пусть две точки системы b1 и b2 действуют друг на друга силами 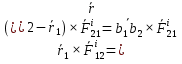 ,  . Определим моменты этих сил относительно некоторой точки о и вычислим сумму этих моментов с учётом третьего закона Ньютона. Имеем  + .Векторы  антипараллельны, след-но  Просуммировав моменты всех внутренних сил, находим:  2-е сво-во внутр. сил.: Cумма моментов всех внутренних сил в механической системе относительно любого центра о равна нулю.  .6.Теорема об изменении кинетического момента механической системы.  . Вектор  – главный момент внешних сил, действующих на мех. систему.Теорема: Производная по времени от кинетического момента механической системы(относительно о) равна главному моменту внешних сил, действующих на систему( отно-но о).  (2)Спроектируем (1) на оси координат.   Спроектируем (2) на оси координат:  Следствия: 1. Внутренние силы не изменяют кинетического момента механической системы. 2.Если главный момент внешних сил(относительно некоторого центра или некоторой оси) равен нулю, то кинетический момент механической системы(относительно этого центра или этой оси) постоянен. (19)Дифференциальные уравнения вращения тела вокруг неподвижной оси. 1.Кинетический момент тела, вращающегося вокруг неподвижной оси. 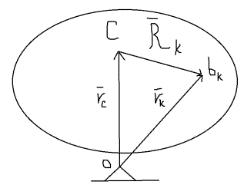 Рассмотрим произвольное движение твёрдого тела и найдём выражение его кинетического момента относ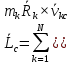ительно некоторого неподвижного начала отсчёта о. Пусть  есть радиус-вектор центра масс тела. Тогда положение произвольной точки тела  определяется вектором    , то  . Получаем:  Здесь  есть кинетический момент, который тело приобретает во вращении вокруг центра масс.2.Дифференциальное уравнения вращения. Пример решения. 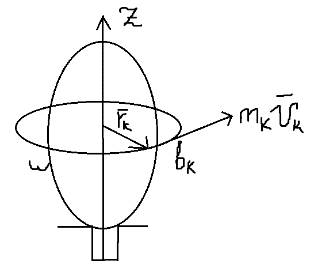  , k=1,k , - пот.кин. момент полож. чтобы учесть пишут  (проекция скорости)1  ,   - кинетический момент тела, вращающегося вокруг неподвижной оси равен произведению угловой скорости тела и момента инерции тела, вычисленному относительно той же оси. ,  ,  - дифференциальное уравнение тела, вращающегося вокруг неподвижной оси.Пример: Рассмотрим вращение диска вокруг неподвижной оси под действием постоянной силы 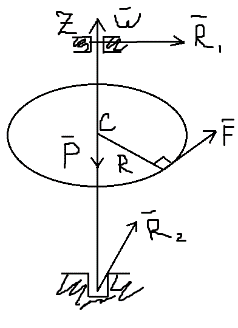. Пусть к ободу диска приложена сила по касательной к нему.  ,  ,  ,  - начальная угловая скорость. ,- при вращении диска вокруг неподвижной оси под действием постоянной силы угол поворота тела  меняется по квадратичному закону в зависимости от времени.  3.Физический маятник и экспериментальное определение моментов инерции. Физическим маятником называетсятвёрдое тело, которое можетсвободно качаться на неподвижной оси. 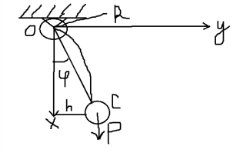 OC=l , вес тела – Р. - дифференциальное уравнение вращения. нелинейное диф.уравнение 2-го порядка. Оно называется диф.уравнением колебаний физ.маятника.Решение этого уравнения в виде конечной формулы записать не удастся, поэтому используем метод линеаризации таких уравнений. Рассмотрим малые колебания маятника. Для таких углов дост. Мощностью 4% имеем  . – диф. Уравнение малых колебаний маятника. Его решение известно:  ,  - константы интегрирования, k- круговая частота колебаний.Спроектируем на плоскость XOY:  Момент инерции тела относительно оси равен сумме произведений масс отдельных точек тела и квадратов расстояний от точки до оси. 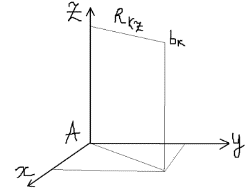 . Моменты инерции относительно осей x и y получим перестановкой символов x, y,z. Пусть N стремится к ∞, а  к 0, тогда записанные суммы превратятся в тройные интегралы вида:   (20)Элементарная теория моментов инерции. 1.Момент инерции стержня и трубы. 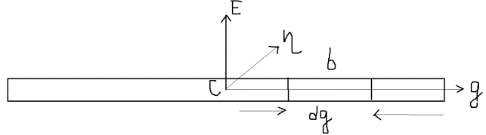 Рассмотрим стержень длиной 2L и выделим в нём бесконечно малый элемент и длиной dg. Если М –масса всего стержня, то масса элемента единичной длины равна M/2L. Поэтому масса точки b есть dm=  . Теперь момент инерции стержня относительно оси СE принимает вид:   Находим  . Аналогично можем определить момент инерции стержня относительно оси оE, проходящей через его торец. При этом изменятся лишь пределы интегрирования:  Момент инерции окружности. 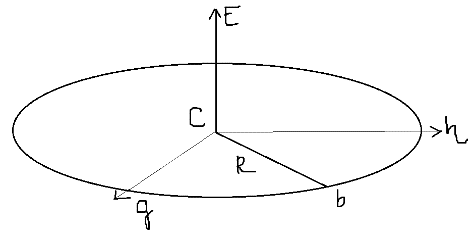 Под окружностью здесь будем понимать тонкую тяжёлую проволоку радиуса R. Вычислим момент инерции относительно оси CE.  . Отсюда  .(21)Статика твёрдого тела. 1.Уравновешенные системы внешних сил. 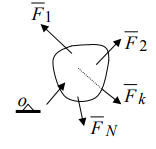 Система сил 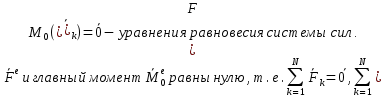 , действующих на твёрдое тело, называется уравновешенной, если её главный вектор  2.Скалярная форма уравнений равновесия произвольной системы сил. Введём декартову систему координат с центром в точке о и спроектируем уравнения равновесия системы сил на оси координат:   Здесь  ,  – моменты произвольной силы  Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на оси координат и суммы моментов всех сил относительно координатных осей были равны нулю. |