Термех. термех. 1 Векторное исчисление Вектор и его модуль

• Название: 1 Векторное исчисление Вектор и его модуль
• Анкор: Термех
• Дата: 09.03.2023
• Размер: 2.59 Mb.
• Имя файла: термех.docx
• Тип: Документы; #976014
• страница: 3 из 6

1.Основное уравнение динамикиматериальной точки

Рассмотрим движение мат. т. B относительно инерциальной системы отсчета. Пусть .. -система реально действующих на точку сил, в число которых входят и реакция связей. Сочетание второго закона Ньютона и принципа незави-ти действия сил приводит к соотношению которое наз-ся основным уравнением динамики мат.точки

2.Дифференциальные уравнения движения материальной точки

ввекторной форме и в проекциях на оси координат имеют вид m (Выражение ускорения через радиус вектор точки b. равнодействующая системы сил ..

Спроектировав формулу на оси декартовой системы координат с центром в неподвижной точке о .(проекции радиус вектора точки на оси координат равны координатам точки r_x=x_b, r_y=y_b,r_z=z_b В результате получим , ,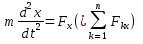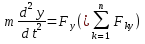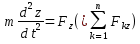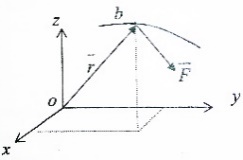




3.Две основные задачи динамики материальной точки

Первая (прямая) задача динамики. Известен закон движения точки x(t), y(t), z(t). Определить равнодействующую всех сил, действующих на точку. Решается дифференцированием координат при использовании дифференциальных уравнений движения.

Вторая (обратная) задача динамики. Известны силы, действующие на материальную точку. Определить закон движения точки. Решается интегрированием дифференциальных уравнений движения.

4. Статика мат. точки, уравнение равновесия.

Пусть точка b неподвижна т.е тогда из m находим (*)Система сил .. действующих на мат. т. для которой выполняется формула(*) наз-ся уравновешенной. Само это соотношение наз-ся уравнением равновесия системы сил, действующих на мат.т.Пусть на точку действует уравновешенная система сил. Тогда из диф. Уравнения движения получаем , или если =0 то мат точка находится в покое .В противном случае она движется равномерно(вектор скорости не изменяется по модулю) и прямолинейно(вектор скорости не изменяется по направлению). Такое движение наз-ся по инерции ВЫВОД: под действинм уравновешенной системы сил мат.т или находится в покое, или движется по инерции

5.Cвободные колебания мат. точки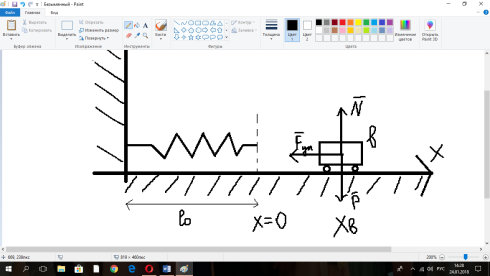



Пусть l₀ длина ненапряженной пружины . введем ось Ох с началос отсчета в конце ненапряженной пружины F_x= – cx, сила стремится вернуть точку в равновесное положение, "с" – коэффициент жесткости пружины F= силе упругости при деформации, равной единице [Н/м].

x:

y: т.к y=const, то N=P; ; к ;

x(t)=C₁sin(kt+C₂₎(*)здесь С₁ и С₂ константы интегр-ия которые опред изначально услов задачи. t=0 должно быть известно положение точки.T=0 x=x₀,V_x=V_x0 продиф (*) по врем и получаем V_x(t)=C₁kcos(kt+C₂)(**) продиф по вр(**) V²x/dt²=-C₁k²sin(kt+C₂) Для опред-ия констант интегрирования(*) и(**) при t=0решаем систему x₀=C₁sinC₂,V₀=-C₁kcosC₂x₀/V₀=tgC₂/kC₂=arctgx₀k/V_0xC₁₌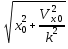

Вся информация о движении мат. т. при известных нач.т. соед-ет всю информацию о движ. Однако иногда требуется не вся инф-ия , а только частичная инф. о движении. Она содержит теор о динамике, а именно теор об изменениях кол-ва движ(теорема об измен. Кинет. Энергии.)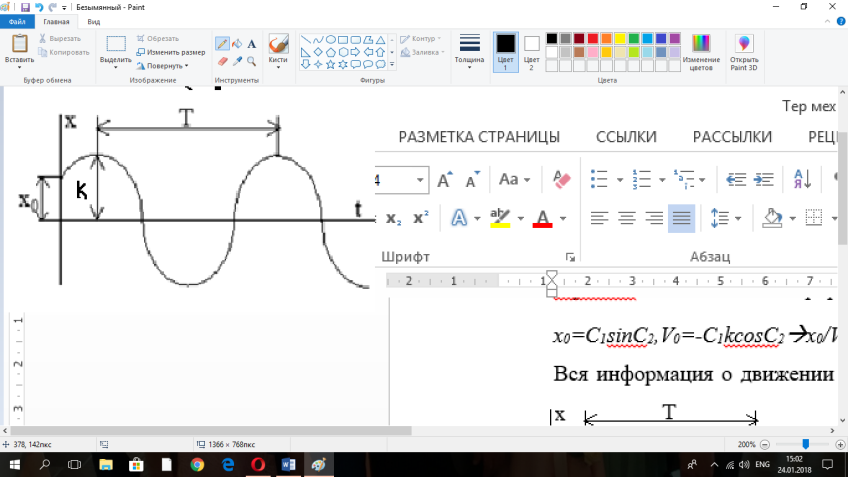
(12)Принцип Даламбера и сила инерции.

Принцип освобождения от связей приводит к появлению пассивных сил(это реакции связи, они сами не вызывают движение точки), принцип равенства действия и противодействия порождает активные силы(Силы способные вызывать движение точки(Вес)).Сумму всех сил действ. На точку ставим, как сумму 2-х сил. 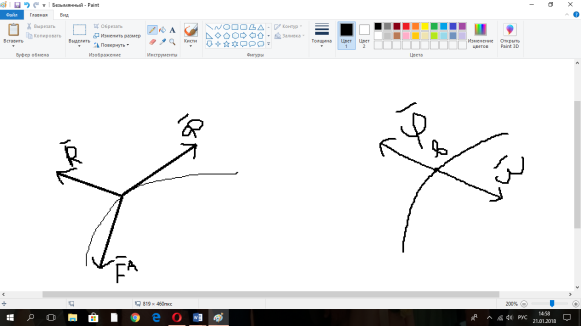где -Сумма всех актив.сил действ на т., -сумма реакций связи.Основное уравнение динамики примет вид m , (-m т.к. складыв-ся только одноименные величины, то выр-ие в скобках имеет смысл силы. Согласно определению вектор силы инерции направлен в сторону выпуклости траектории. Возьмем модуль от последней формулы(Модуль силы инерции равен массе точки* на модуль ускорения уравнение равновесия



Принцип Даламбера: активные силы и реакции связей при любом движении мат. т. всегда можно уравновесить силой инерции.Принятие этого принципа означает переход от неподвижной( инерциальной) системы отсчетаохуz, к подвижной системе координат. При этом вводится сила инерции и основное уравнение динамики заменяется уравнением равновесия.
(13)Общие сведения о механической системе.
1.Определение и примеры механических систем. Механической системой наз-ся совокупность матер. точек, движения которых взаимосвязаны. Рассмотри два тяжелых шарика b₁ и b₂, соединённых тонким стержнем, массой которого можно принебречь по сравнению с массами шаров. Их движение в свободном полете связаны таким образом, что расст-е м-у ними всегда остается неизменным. Здесь мы имеем пример так называемой неизм. мех. сист. Если шары соединить невесомой пружиной, то расстояние м-у шарами при движении может меняться – система изменяемая. Тв. тело как мех. сис-ме можно трактовать по-разному в завис-ти от того, что считать мат т. сис-мы. При дроблении мат. т. принимают мелкую частицу тела. И получают мех. сис-му, состоящую из большого числа точек. Любое тело можно рассматривать как мех. сис-му вопрос заключается лишь в том, что выбирается в качестве мат. т. в сис-ме. Далее будем пользоваться след сис-мой обозн. мат. т. – в₁,…, в_к,…,в_n.; в_к – произвольн. т. в сис-ме; м_к – ее масса; =M – масса всей системы; – радиус вектор к к-той т.; – ее скорость.


2.Внешние и внутренние силы.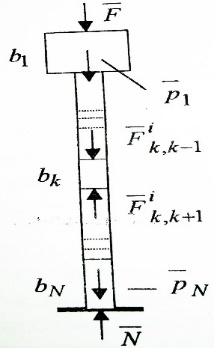

Внешними силами действ. на точки мех. сис-мы наз-ся силы, возникающие в рез-те взаимодействия точек сис-мы с телами не входящ. в сис-му и обозн. . Внутр. силами будем называть силы возникающ. в рез-те взаимодейств. точек сис-мы м-у собой и их обозн. . В качестве примера мех. сис-мы рассмотрим массивную бетонную колонну под верт. нагрузкой F. В кач-ве мат. точки в колонне примем отдельный слой колонныb_k. На нее действует 2 внутренние силы: точка c силой таким образом внутренних ил очень много. Внешними силами здесь являются силы тяжести , нагрузка F на точку b_1, а на точку b_N реакция опоры

3.Первое св-во внутр. сил в мех. сис-ме.
Пусть т. b₁ действует на т b₂ силой , пусть т. b₂ действует на т b₁ силой . . . Если про суммируем все внутр. силы в мех сис-ме, то произойдет их взаимное уничтожение в рез-те получим (*). Сумму всех внутр. сил действ. на т. =b_к обозначим ; . При любом движ-и мех. сис-мы и в сост. покоя сумма всех внутр. сил в сис-ме равна нулю.


(14)Теорема о движ-и центра масс мех. сис-мы.
Определение центра масс.
Центр масс мех. сис-мы будем называть т. С, положение которой определяется соотношением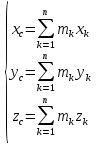

, где . Спроектируем 1е ур-е на оси декартовых коор-т

;



(15)Вывод теоремы одвижения центра масс.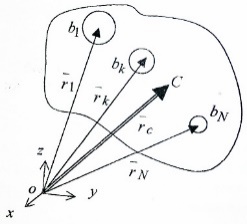

Продифф-ем 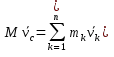по времени 1). Продиф-ем (1) по времени (*) запишем основное ур-е динамики для т. b_к. Сумму всех внешних сил действующих на т b_к обозначим , сумму всех внутр сил - . Запишем второй з-н Ньютона для b_к , k= 1→n. Просуммируем все эти соотношения , пусть – главный вектор внешних сил действ. на сис-му. С исп-ем (*) последняя ф-ла примет вид . Т.к. т. С в общем случае может не принадлежать мех. сис-ме, т.е. явл-ся абстрактной точкой формулировку теоремы запишем в виде Т. центр масс мех. си-мы расценивается обычная матер. Точка, масса которой равна массе всей системы и к которой приложены все действующие внешние силы, действующие на систему. I) в ф-лу (2) не входят внутр. силы входящ. в систему. Внутр силы в системе не влияют на движ-е центра масс. II) Пусть , тогда , тк , то не поворачивается т.е. ЦМ движется по прямой и не меняется по модулю. ЦМ движется равномерно. Если , то ЦМ движется прямолинейно но и равномерно, либо нах-ся в покое. III) Пусть пусть проекция главн. вектора сил равна нулю, тогда спроектир (2) на ОХ Х: MW_cx= 0; V_cx= const. Если , то проекция на ОХ постоянна.

(16)Теорема об изменении кол-ва движения.
1.Определенный интеграл от вектора.
Рассмотрим произв. вектор и промежуток времени [0;Т], запишем опр-е интегралом от за время Т будем называть вектор обозначаемый и определенный ф-лой (46). Формулой (46) вычисление интеграла от вектора сведено к вычислению 3-х интегралов от скалярной функции вектора на оси декартовых коор-т. Определенный интегралл от вектора есть константа.
2.Импульс силы.
Пусть т. b движется под действием силы , за бесконечно малый промежуток времени dt из положения b она перейдет в положение b’, так что bb’ – бесконечно мала.
Импульсом за бесконечное малое время dt будем называть вектор d 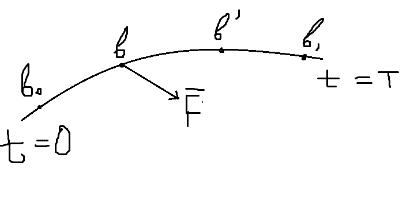с определенной формулой d = dt. Из определения следует, что d параллелен . Рассмотрим конечное перемещение от положения b₀ до b₂, импульсом силы F за время Т будем называть вектор определенный ф-лой , , , . Импульс пост. силы равен произведению вектора силы и времени.


3.Теорема об изменении количества движения материальной точки.
Количеством движения материальной точки будем называть вектор 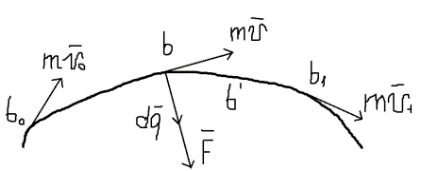, равный произведению массы точки и её вектора скорости. Итак, .

Модуль вектора количества движения определяется соотношением q=mv.
Рассмотрим движение отдельной материальной точки под действием некоторой системы сил с равнодействующей и запишем для нее основное уравнение динамики: .(1)
Внесем массу точки под знак производной, в результате получим .(2)
Итак, производная от вектора количества движения материальной точки равна равнодействующей сил, действующих на точку.
Последнюю формулу часто представляют иначе. Ее правую и левую части на бесконечно малый промежуток времени dt. В результате получаем теорему об изменении количества движения точки в дифференциальной форме: (3). Являясь полным дифференциалом, элементарный импульс равнодействующей силы равен дифференциалу количества движения материальной точки.
Рассмотрим конечное перемещение точки от положения b₀ до положения b₁ за промежуток времени [0, T]. Возьмем интеграл по времени от правой и левой части формулы (2). Имеем или . В результате получим (4)
Изменение количества движения материальной точки (за некоторый промежуток времени) равно сумме импульсов всех сил, действующих на точку ( за этот промежуток времени).
Спроектировав (4) на оси координат, получим : (также для y и z).

4.Количество движения механической системы.
Пусть движется произвольно мех. система. Кол-вом движения мех. сис-мы будем называть вектор 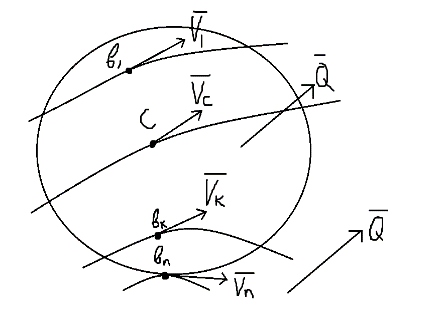согласно
получим, что .

Рассмотрим 2-а частных случая поступательных движ-я тверд. тела.
1)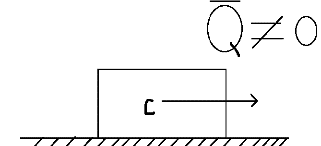
2)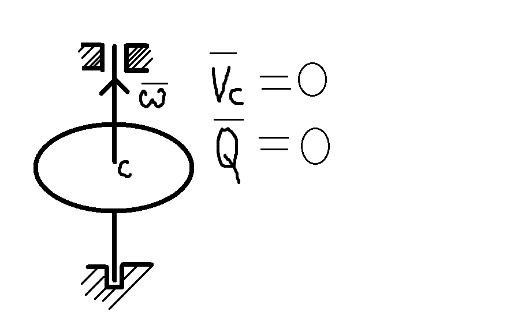
Учитывая эти два случая говорят, что кол-во движения тверд. тела характеризует поступательную часть движения.

5.Теорема об изменении количества движения механической системы.
Рассмотрим движение механической системы. Для произвольной точки :
Просуммируем все эти соотношения: , рассмотрим каждую из трёх полученных сумм. Слева имеем : .
Теорема в диф. форме: 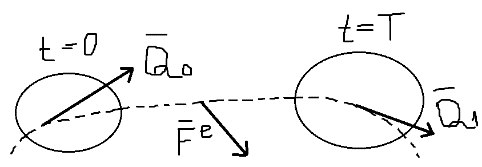Производная по времени от вектора количества движения механической системы равна главному вектору внешних сил.

Пусть в начальный момент времени t=0 система имела количество движения . В момент времени t=T количество движения обозначим . Проинтегрируем (1) в пределах от 0 до Т. Тогда или (2)– теорема в интегральной форме. Здесь - импульс главного вектора внешних сил. .
В проекциях на оси координат имеем : (также для y и z).
Следствия:
1. Внутренние силы не влияют на количество движения механической системы.
2.Если главный вектор внешних сил равен нулю, то количество движения механической системы постоянно.
3. Если проекция главного вектора внешних сил на какую-либо ось равна нулю, то проекция количества движения механической системы на эту ось постоянна.
Примеры.
Давление струи на колено трубы. Теорему об изменении кол-ва движ-я в системе часто используют при исследовании жидкости. Рассмотрим колено трубы диаметром d. по которой жидкость плотностью p бежит со скоростью V₀ двумя сечениями выделим объем жидкости. За время Т этот объем перейдет в положение a’b’, 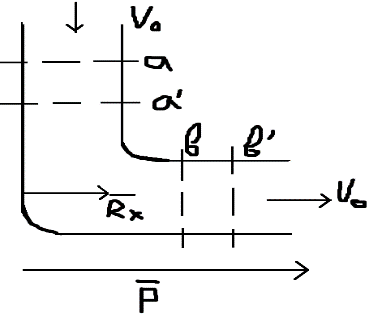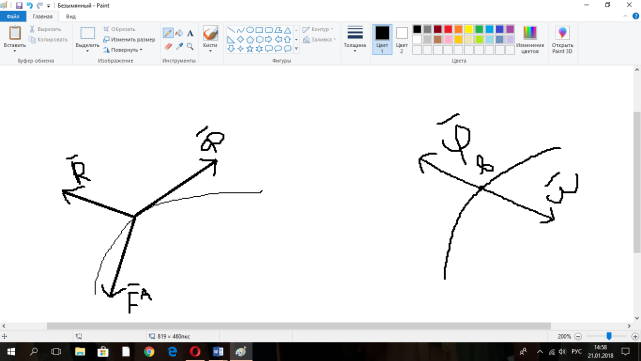– сила с которой стенка трубы давит на объем.

; = .
, согласно формуле и (*) получаем .
(17)Момент вектора.

I.Определение момент вектора относительно точки (центра).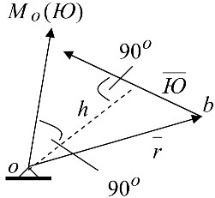



Моментом вектора относительно точки О будем называть вектор, обозначенный и определяемый формулой

Момент вектора относительно точки (центра) равен векторному произведению радиус-вектора точки b и самого вектора.

Согласно условиям векторного умножения плоскости векторов согласно правилу правого винта.



Плечом вектора относительно точки О будем называть длину перпендикуляра h, опущенного на линию действия вектора .

h= rsinα.

Модуль момента равен произведению модуля исходного вектора и плеча.


II. Скалярное определение момента вектора относительно точки.

Существуют задачи, в которых все вектора описывающие механические явления лежат в некоторой плоскости (плоские задачи). В таких задачах вектор будет перпендикулярен плоскости и нарушит плоскую картину явления. В этом случае дается упрощенное определение момента, который вводится как скалярная величина



Моментом вектора относительно точки О в скалярном смысле будем называть скаляр, обозначаемый и определяемый формулой

Момент вектора относительно точки О в скалярном смысле равен взятому соответствующим знакам произведения модуля вектора на плечо h,

Знак «+» в этой формуле следует ставить, когда вектор вращает свое плечо L вокруг точки О против часовой стрелки
III.Момент вектора относительно координатных осей.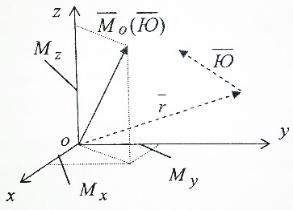



Определим момент вектора относительно оси z. Для этого спроектируем на плоскость XY. Разложим вектор на две составляющие вдоль оси X и Y. . Момент вектора относительно точки О момент в скалярном смысле равен , , тогда



Аналогично:





\

Для определения момента вектора относительно оси z надо спроектировать вектор на плоскость XOY и найти момент вектора относительно точки О

IV.Теорема о моменте суммы.

Пусть в точке b приложены несколько векторов 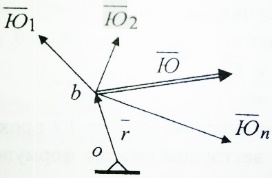, , . Пусть .



Запишем момент вектора 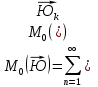относительно точки О





Теорема: Момент силы равен сумме моментов

V.Момент вектора как характеристика вращения.



Пусть линия вектора проходит через точку 0, тогда вектора и параллельны и их произведение равно нулю.



Рассмотрим, когда равно нулю.



Оба этих случая объединяет тезис. Вектор не создает вращение вокруг точки О. Учитывая это говорят, что момент вектора относительно точки характеризует «вращение» вокруг точки.

Рассмотрим случай, когда момент относительно оси равен нулю.