Теорема. При поступат. движ. все точки тела имеют наложимые траектории, одинак. скорости и ускорения.
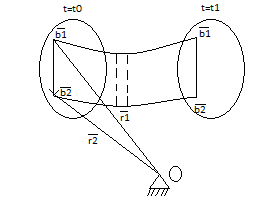
Рассмотрим вектор b1b2. При движении он не меняет своей длины т.к. тело абс. тв. Он не меняет своего направления, т.к. движ-е поступательное 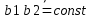 введем начало отсчета О и проведем введем начало отсчета О и проведем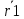 и и 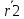 . т.к. при движении тела треугольник Оb1b2 замкнут, то при любом t согласно правилу сложения векторов треугольника вып-ся формула . т.к. при движении тела треугольник Оb1b2 замкнут, то при любом t согласно правилу сложения векторов треугольника вып-ся формула 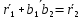 при любом t. т.к траектория т b2 получается сдвигом на пост. вектор траектории т. b1, то эти траектории наложимы. Продиф-ем последнюю ф-лу. по t. при любом t. т.к траектория т b2 получается сдвигом на пост. вектор траектории т. b1, то эти траектории наложимы. Продиф-ем последнюю ф-лу. по t. 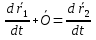 ; V1=V2. Продиф-вав последнее соотношение по времени получим ; V1=V2. Продиф-вав последнее соотношение по времени получим 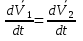 ; W1=W2. При поступательном движении все точки тела имеют одинак. скорость инаправление, поэтому при поступат. движ-ии можно ввести понятие «скорость тела» и «ускорение тела». Уравнение движения определяется заданием координат любой точки тела x = x(t), y = y(t), z = z(t). ; W1=W2. При поступательном движении все точки тела имеют одинак. скорость инаправление, поэтому при поступат. движ-ии можно ввести понятие «скорость тела» и «ускорение тела». Уравнение движения определяется заданием координат любой точки тела x = x(t), y = y(t), z = z(t).
(6)Вращение твердого тела вокруг неподвижной оси.
1.Уравнение вращательного движения.
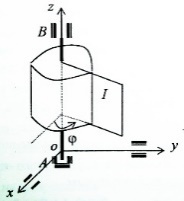
При вращении тела его угол поворота 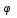 с течением времени меняется т.е. с течением времени меняется т.е. 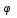 = =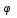 (t)(*), если это соотнош. известно при любом t, то говорят задан закон вращат. движ-я тела, (*) - ур-е вращения. Угол поворота считается «+», если тело повернулось против хода часовой стрелки, при этом следует указать ось вращения и отметить «+» напр-е отсчета следует смотреть с положит напр-я оси z. (t)(*), если это соотнош. известно при любом t, то говорят задан закон вращат. движ-я тела, (*) - ур-е вращения. Угол поворота считается «+», если тело повернулось против хода часовой стрелки, при этом следует указать ось вращения и отметить «+» напр-е отсчета следует смотреть с положит напр-я оси z.
 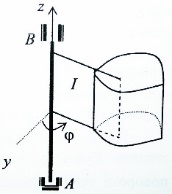
2.Угловая скорость.
Угловой скоростью тела в скаляр. смысле будем называть скаляр 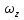 определенный формулой определенный формулой 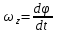 . .
Вектором угловой скорости тела будем называть вектор определенный ф-лой 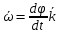 , , – единичный вектор оси вращения oz. Определенны так вектор угловой скорости будет параллелен или антипараллелен оси вращения. – единичный вектор оси вращения oz. Определенны так вектор угловой скорости будет параллелен или антипараллелен оси вращения.
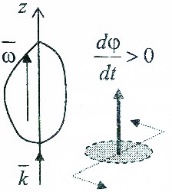 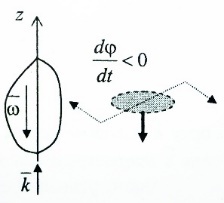
Возьмем модуль от ф-лы 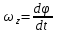 получим получим 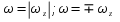 от сюда следует, что угловая скорость от сюда следует, что угловая скорость 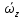 в скалярном смысле есть проекция вектора в скалярном смысле есть проекция вектора 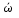 на ось вращения. на ось вращения.
3.Угловое ускорение.
Вектором углового ускорения тела будем называть вектор 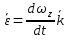 . ε>k, то . ε>k, то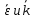 – параллельны;ε – антипараллельны. – параллельны;ε – антипараллельны. 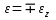 ; ;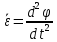 ; ; 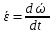 . Вектор углового ускорения равен произвдной по времени от вектора угловой скорости. Угловым ускорением тела в скалярном смысле называется скалярная величина . Вектор углового ускорения равен произвдной по времени от вектора угловой скорости. Угловым ускорением тела в скалярном смысле называется скалярная величина 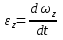 , , 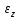 – проекция углового ускорения на ось вращения. Имеем 2-а варианта: – проекция углового ускорения на ось вращения. Имеем 2-а варианта: 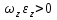 – то это схема разгона, угловая скорость увеличивается по мудулю. – то это схема разгона, угловая скорость увеличивается по мудулю. 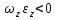 – то это схема торможения, угловая скорость уменьшается по модулю. Т.к. – то это схема торможения, угловая скорость уменьшается по модулю. Т.к. 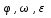 не связаны с конкретн. т. тела, заключим что угол поворота, угловая скорость и угловое уск-е, характеристики всего тела. не связаны с конкретн. т. тела, заключим что угол поворота, угловая скорость и угловое уск-е, характеристики всего тела.
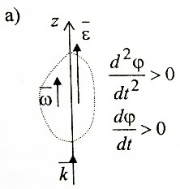 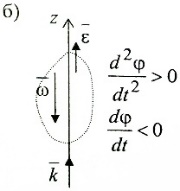
4.Уравнения равномерного и равнопеременного движения.
Вращ-е теларавномерное, если 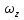 =const. Определим ур-е равномерного движ. =const. Определим ур-е равномерного движ. 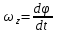 проинтегр. по времени проинтегр. по времени 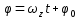 , , 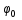 = углу поворота при t=0, = углу поворота при t=0, 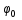 – нач. угол поворота тела. – нач. угол поворота тела.
Вращение тела вокруг неподвижной оси наз-ся равнопеременным, если угловое ускор-е постоянно, т.е. 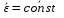 . Проинтегрировав . Проинтегрировав 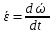 , получим , получим 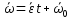 , затем спроектируем на ось вращения, получим , затем спроектируем на ось вращения, получим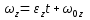 , проинтегрируем по времени и получим уравнение равнопеременного вращ-я: , проинтегрируем по времени и получим уравнение равнопеременного вращ-я: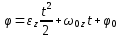 . .
5.Скорость и ускорение точек тела при вращении вокруг неподвижной оси.
Скорость точек тела вращ. вокруг неподвижн. оси .
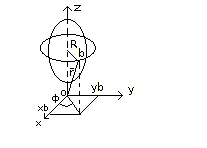
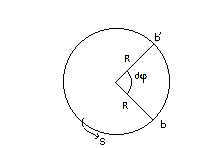
b – произв. точка; R – расст. от b до оси вращ-я.
Спроектируем т. b на пл. Оху: rx=xb=Rcosф; ry=yb=Rsinф; rz=zb=const;
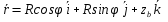 продиф-ем по t, продиф-ем по t, 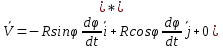 . Рассмотрим выражение . Рассмотрим выражение 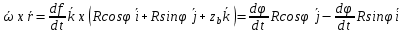 , получаем , получаем 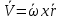 . Вектор скорости точки тела равен векторному произведению угловой скорости и радиусвектора точке, согласно правилу правого винта . Вектор скорости точки тела равен векторному произведению угловой скорости и радиусвектора точке, согласно правилу правого винта 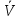 будет направлен по касат. к траектории. будет направлен по касат. к траектории. 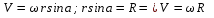 . Модуль скорости точки равен произведению модуля угловой скор. тела и расст. до оси вращнения. . Модуль скорости точки равен произведению модуля угловой скор. тела и расст. до оси вращнения.
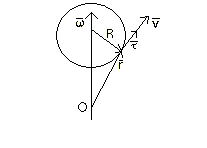
Рассмотрим б.м. отрезок времени dt при этом т. b перейдет в положение b’ при этом тело повернется на б.м. угол dф. Длина дуги bb’ = dS = Rdф. Поделим это соотнош. на dt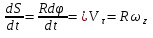
Ускорение точек вращ. тела продиф-ем 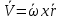 по времени по времени 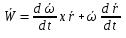 (***). Обозначим (***). Обозначим 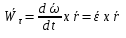 ; ; 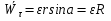 . Обозначим . Обозначим 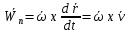 ; ; 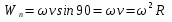 . Теперь (***) примет вид . Теперь (***) примет вид 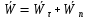 . .
7)Сферическое движения твердого тела.
1.Углы Эйлера.
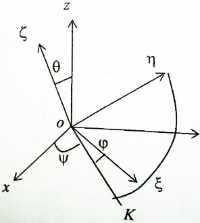
Рассмотрим прямую ОК – линию пересечения плоскостей ОХУ и 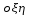 ( эта прямая наз-ся линией узлов). Зададим угол ф м-у прямой оК и осью ( эта прямая наз-ся линией узлов). Зададим угол ф м-у прямой оК и осью 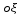 (этот угол наз-ся углом собственного вращения) и угол (этот угол наз-ся углом собственного вращения) и угол 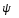 м-у прямой оК и осью м-у прямой оК и осью 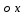 (угол прецессии). Третий угол (угол прецессии). Третий угол 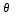 есть угол м-у осями ОZ и есть угол м-у осями ОZ и 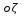 ( угол нутации). Придвижении тела в общем случае углы Эйлера с течением времени меняются ( угол нутации). Придвижении тела в общем случае углы Эйлера с течением времени меняются 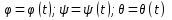
Задание этих углов в любой момент времени позволяет определить положение тела в пространстве, жестко связанного с подвижными осями. Данное ур-е наз-ся ур-ем движ-я.
2.Вектор угловой скорости.
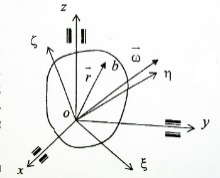
Выберем в движущемся теле произвольную точку b проекцией ее радиус вектора  на оси коор-т подвижной и неподвижной систем совпадают с коор-тами точки в этих системах. В неподвижной системе коор-т на оси коор-т подвижной и неподвижной систем совпадают с коор-тами точки в этих системах. В неподвижной системе коор-т 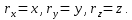
При движении тела положение точки b по отношению к неподвижной системе коор-т изм-ся, следовательно, ее коор-ты x, y, z, есть ф-ции времени. Величины 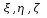 от времени не зависят, т.к. по отношению к подвижной системе отсчета точка b не меняет своего положения. от времени не зависят, т.к. по отношению к подвижной системе отсчета точка b не меняет своего положения.
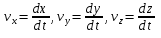 после проведения некоторых операций получим после проведения некоторых операций получим
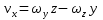 , , 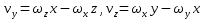
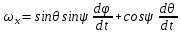 , , 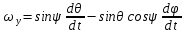 , , 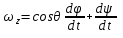 . .
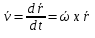 . .
Эту формулу можно спроектировать но оси подвижной системы коор-т О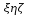 . Получим: . Получим: 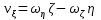 , , 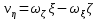 , , 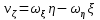 . .
3.Мгновенная ось вращения.
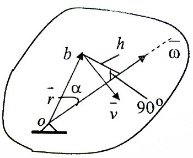
Рассмотрим вопрос о направлении вектора скорости произвольной точки b, находящейся в движ. теле. т.к. тело считаем абс. тверд. ob=r не меняется, однако отрезок ob в общем случае поворачивается вокруг неподвижного начала отсчета. Это означает, что траектория т. b лежит на пов-ти сферы радиуса rc центром в т. О. Вектор скорости точки лежит в плоскости, которая касается пов-ти сферы. В этой связи движ-е тела с одной неподвижной точкой называют сферическим движением. При сферическом движении в любой момент времени существуют точки тела, скорость которых равна нулю. Их положение определяется по формуле 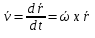 в которой полагаем в которой полагаем 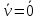 . Если . Если 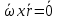 , то вектор угловой скорости и радиус-вектор искомых точек параллельны, и проекции этих векторов пропорциональны. , то вектор угловой скорости и радиус-вектор искомых точек параллельны, и проекции этих векторов пропорциональны. 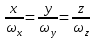 . Последнее соотношение представляют собой ур-е прямой, проходящей через точку О параллельно вектору угловой скорости . Последнее соотношение представляют собой ур-е прямой, проходящей через точку О параллельно вектору угловой скорости 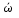 эта прямая наз-ся мгновенной осью вращения. эта прямая наз-ся мгновенной осью вращения.
4.Скорость и ускорение точек тела.
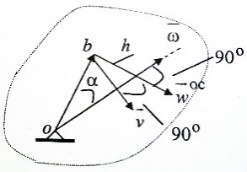
Скорость произвольной точки b тела определяется соотношениями 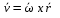 ; ; 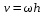 . Здесь h - расстояние от точки b до мгновенной оси вращения. . Здесь h - расстояние от точки b до мгновенной оси вращения.
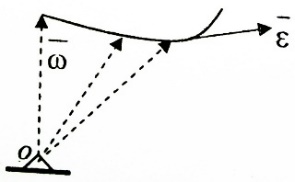
Определим вектор ускорения произвольной точки тела. Продифференцируем ур-е 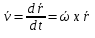 по времени. В рез-те получим по времени. В рез-те получим 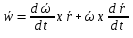 , где , где 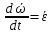 – вектор углового ускорения тела при сферическом движении. – вектор углового ускорения тела при сферическом движении.
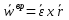 , где , где 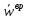 – вращательное ускорение точки b. – вращательное ускорение точки b.
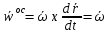 х х  , где , где 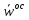 – осестремительное ускорение т b. – осестремительное ускорение т b.
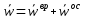  
(8)Свободное движение твердого тела.
Движение твердого тела без каких-либо доп. ограничений называется свободным
1.Две составляющие свободного движения.
Рассмотрим два положения свободнодвижущегося тела в разные моменты времени. С этой целью выберем в теле произвольную точку 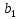 и назовем ее полюсом. Выберем еще 2 точки и назовем ее полюсом. Выберем еще 2 точки 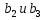 так, чтобы все эти 3 точки образовали треугольник. так, чтобы все эти 3 точки образовали треугольник.
За промежуток времени от 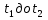 треугольник треугольник 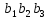 вместе с телом изменит свое положение. Переход из одного положения в другое можно осуществить в 2 этапа. 1) Перенос тела вместе с полюсом вместе с телом изменит свое положение. Переход из одного положения в другое можно осуществить в 2 этапа. 1) Перенос тела вместе с полюсом 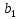 без поворота. 2) Вращая треугольник вокруг без поворота. 2) Вращая треугольник вокруг 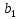 завершим перевод тела из первого положения во второе. Здесь вращение понимается, как сферическое движение вокруг полюса. завершим перевод тела из первого положения во второе. Здесь вращение понимается, как сферическое движение вокруг полюса.
Произвольное движение свободного тв. тела складывается из поступательного движения вместе с полюсом и вращения вокруг этого полюса
2.Скорость и ускорение точек тела при свободном движении.
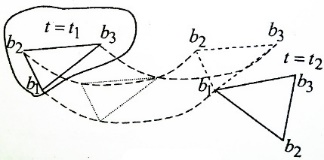
Положение полюса 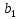 и произвольной точки тела и произвольной точки тела 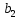 определено радиус-векторами определено радиус-векторами 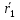 и и 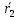 , которые связаны соотношением , которые связаны соотношением 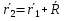
Продифференцировав его по времени, находим
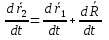 (1) (1)
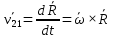 Тогда (1) примет вид: Тогда (1) примет вид: 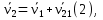 здесь здесь 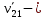 скорость, кот. т. скорость, кот. т. 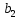 имеет при вращении тела вокруг т. имеет при вращении тела вокруг т. 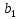
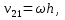 h-расстояние от точки h-расстояние от точки  до мгновенной оси вращения до мгновенной оси вращения
Скорость  произвольной точки тела складывается из скорости полюса произвольной точки тела складывается из скорости полюса  и скорости и скорости 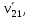 которую точка которую точка 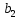 имеет за счет вращения вокруг полюса имеет за счет вращения вокруг полюса 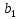
Спроектируем (2) на направление отрезка 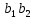 , в результате: , в результате: 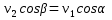
Проекция скоростей двух точек тела на направление отрезка, соединяющего эти точки, равны между собой.
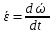
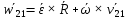
Ускорение 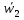 произвольной точки тела в свободном движении складывается из ускорения полюса произвольной точки тела в свободном движении складывается из ускорения полюса 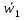 и ускорения и ускорения 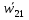 ( за счет вращения тела вокруг полюса) ( за счет вращения тела вокруг полюса)
3.Теорема о проекциях скоростей двух точек.
Положение полюса 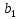 и произвольной точки тела и произвольной точки тела 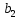 определено радиус-векторами определено радиус-векторами 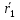 и и 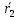 , которые связаны соотношением , которые связаны соотношением 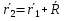
Продифференцировав его по времени, находим
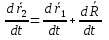 (1) (1)
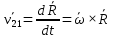
Тогда (1) примет вид: 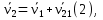 здесь здесь 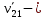 скорость, кот. т. скорость, кот. т. 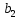 имеет при вращении тела вокруг т. имеет при вращении тела вокруг т. 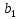
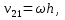 h-расстояние от точки h-расстояние от точки 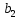 до мгновенной оси вращения до мгновенной оси вращения
Скорость 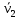 произвольной точки тела складывается из скорости полюса произвольной точки тела складывается из скорости полюса 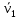 и скорости и скорости 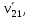 которую точка которую точка 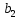 имеет за счет вращения вокруг полюса имеет за счет вращения вокруг полюса 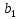
Спроектируем (2) на направление отрезка 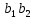 , в результате: , в результате: 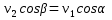
Проекция скоростей двух точек тела на направление отрезка, соединяющего эти точки, равны между собой.
(9)Плоское движение твердого тела.
1.Составляющие движения плоской фигуры.
Движение твердого тела называется плоскопараллельным (или плоским), если траектории всех точек в теле параллельны некоторой неподвижной плоскости.
Проекция тела на неподвижную плоскость-плоская фигура.
Рассмотрим два положения плоской фигуры в разные моменты времени. Выберем на плоской фигуре некоторую точку 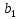 и назовем ее полюсом. Произвольное движение плоской фигуры разлагается на поступательное движение вместе с полюсом и вращение вокруг полюса на некоторый угол γ. и назовем ее полюсом. Произвольное движение плоской фигуры разлагается на поступательное движение вместе с полюсом и вращение вокруг полюса на некоторый угол γ.
Уравнение движения плоской фигуры: 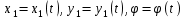
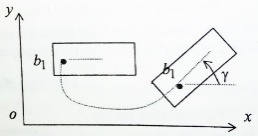
2.Скорость точек плоской фигуры.
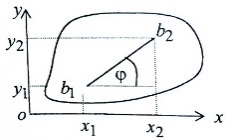
Рассмотрим вопрос об определении скорости произвольной точки плоской фигуры  . Ее координаты выражаются через координаты полюса следующим образом: . Ее координаты выражаются через координаты полюса следующим образом: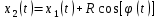 ; ; 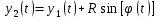 , где , где 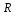 -расстояние от произвольной точки до полюса -расстояние от произвольной точки до полюса
Продифференцировав по времени получим:
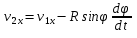 ; ;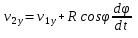
Умножим первое на орт 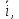 а второе на орт а второе на орт  и сложим их: и сложим их:
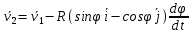 Рассмотрим вектор Рассмотрим вектор 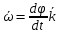 - вектор углового ускорения плоской фигуры.Он направлен перпендикулярно плоскости ОХУ. Знак его проекции - вектор углового ускорения плоской фигуры.Он направлен перпендикулярно плоскости ОХУ. Знак его проекции 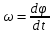 на ось OZ зависит от направления вращения плоской фигуры вокруг полюса. Модуль вектора угловой скорости определяется по фор-ле на ось OZ зависит от направления вращения плоской фигуры вокруг полюса. Модуль вектора угловой скорости определяется по фор-ле 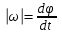 . Рассмотрим выражение . Рассмотрим выражение 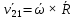 , где , где 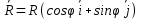 . Согласно правилу векторного умножения вектор . Согласно правилу векторного умножения вектор 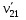 перпендикулярен векторам перпендикулярен векторам 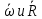 , т.е. параллелен плоскости оху => , т.е. параллелен плоскости оху =>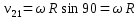 . .
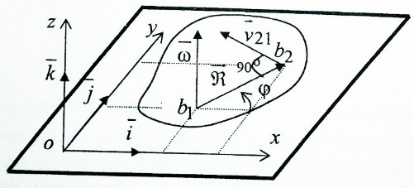
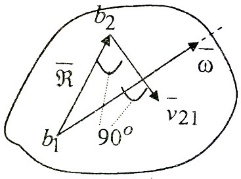
Умножим векторы 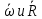 получим получим 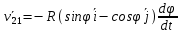 из этого следует из этого следует 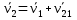 скорость произвольной b2 плоской фигуры складывается из скорости скорость произвольной b2 плоской фигуры складывается из скорости 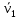 полюса и скорости полюса и скорости 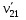 , которую т. b2 имеет при вращении вокруг полюса b1. Спроектируем , которую т. b2 имеет при вращении вокруг полюса b1. Спроектируем 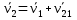 на направление b1b2. Получим на направление b1b2. Получим 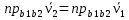 . Проекции скоростей двух точек плоской фигуры на направление прямой, проходящей через эти точки, равны между собой. . Проекции скоростей двух точек плоской фигуры на направление прямой, проходящей через эти точки, равны между собой.
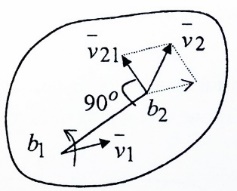
3.Мгновенный центр скоростей плоской фигуры.
Точка плоской фигуры, скорость которой равна нулю называется мгновенным центром скоростей плоской фигуры (МЦС) и обозначается т. р. Таким образом 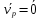 . Если угловая скорость плоской фигуры отлична от нуля, то мгновенный центр скоростей существует. В каждое мгновение движение плоской фигуры можно представить, как вращение вокруг мгновенного центра скоростей. Модуль скорости любой точки равен произведению модуля угловой скорости и расстояния от точки до МЦС, т.е. . Если угловая скорость плоской фигуры отлична от нуля, то мгновенный центр скоростей существует. В каждое мгновение движение плоской фигуры можно представить, как вращение вокруг мгновенного центра скоростей. Модуль скорости любой точки равен произведению модуля угловой скорости и расстояния от точки до МЦС, т.е. 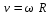 , здесь , здесь 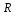 - мгновенный радиус точки. - мгновенный радиус точки.
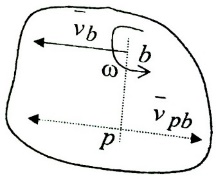
4.Ускорение точек плоской фигуры.
Продифференцируем 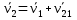 по времени получим по времени получим 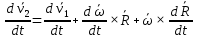 . Здесь . Здесь 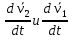 ускорения точек b1 и b2. Вектор ускорения точек b1 и b2. Вектор 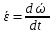 – вектор углового ускорения плоской фигуры и направлен перпендикулярно плоскости ОХУ. – вектор углового ускорения плоской фигуры и направлен перпендикулярно плоскости ОХУ.
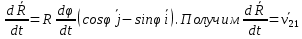 . В результате получим . В результате получим 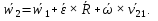
Рассмотрим вектор 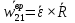 , учитывая правило векторного умножения, получим вектор , учитывая правило векторного умножения, получим вектор 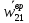 перпендикулярен отрезку b1b2 и его модуль есть перпендикулярен отрезку b1b2 и его модуль есть 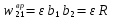 , , 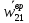 – вращательное ускорение. – вращательное ускорение.
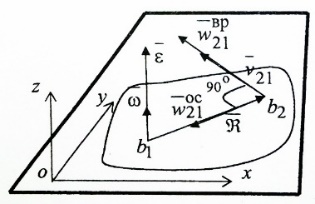
Вектор 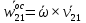 он называется осестремительным ускорением. В соответсвии с правилом правого винта он направлен к полюсу b1. Определив модуль векторного произведения получим он называется осестремительным ускорением. В соответсвии с правилом правого винта он направлен к полюсу b1. Определив модуль векторного произведения получим 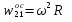 . Окончательный вид принимает формула . Окончательный вид принимает формула 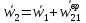 + +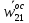 . Т.к. движ-е плоской фигуры складывается из поступательного движения вместе с полюсом b1 и вращением вокруг этого полюса, то структура полученной формулы будет ясна. Вектор . Т.к. движ-е плоской фигуры складывается из поступательного движения вместе с полюсом b1 и вращением вокруг этого полюса, то структура полученной формулы будет ясна. Вектор 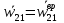 + +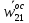 , есть ускорение, которое точка b2 имеет за счет вращения вокруг точки b1. Полное ускорение точки b2 складывается из ускорения , есть ускорение, которое точка b2 имеет за счет вращения вокруг точки b1. Полное ускорение точки b2 складывается из ускорения 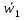 , которое точка b2 имеет, двигаясь вместе с точкой b1, и вектора , которое точка b2 имеет, двигаясь вместе с точкой b1, и вектора 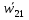 , связанного с вращением плоской фигуры. , связанного с вращением плоской фигуры.
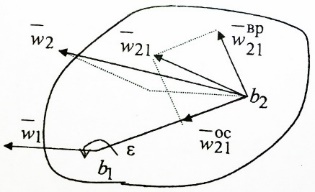
5.Мгновенный центр ускорений.
Если движение плоской фигуры не является поступательным, то можно найти точку, ускорение которой в рассматриваемый момент времени равно нулю. Такая точка q - мгновенный центр ускорений плоской фигуры 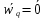 . Запишем формулу для ускорения принимая в качестве полюса точку q, получим . Запишем формулу для ускорения принимая в качестве полюса точку q, получим 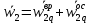 . Таким образом, ускорение произвольной точки b2 формируется только за счет вращения вокруг точки q. Определим угол, который вектор . Таким образом, ускорение произвольной точки b2 формируется только за счет вращения вокруг точки q. Определим угол, который вектор 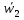 составляет с отрезком b2q. Имеем составляет с отрезком b2q. Имеем 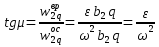 . Величина угла наклона вектора ускорения любой точки к отрезку, соединяющему эту точку с мгновенным центром ускорений, для всех точек плоской фигуры одинакова. . Величина угла наклона вектора ускорения любой точки к отрезку, соединяющему эту точку с мгновенным центром ускорений, для всех точек плоской фигуры одинакова.
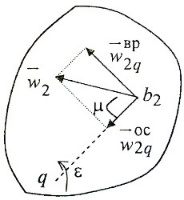 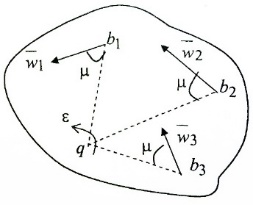
Модули ускорения различных точек в общем случае будут различны. Для точки b2 находим
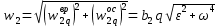 . Чем дальше от мгновенного центра ускорений находится точка, тем больше ее ускорение. . Чем дальше от мгновенного центра ускорений находится точка, тем больше ее ускорение.
(10)Основные законы динамики материальной точки
1.Понятие мат. точки
Материальной точкой называется тело конечной массы, размерами которого можно пренебречь. Далее m -масса материальной точки.
Вывод : возможность пренебрегать или не пренебрегать размерами тела зависит от характера решаемой механической задачи.В одних задачах данное тело является материальной точкой, в других задачах его следует рассматривать как механическую систему.
2.Принцип освобождения от связей.
Связью называется все то, что ограничивает свободное перемещение материальной точки.(Мат. Точкой называется свободной, если на ее перемещение не наложено никаких ограничений.Реакцией связи называется сила, которой связь действует на материальную точку. Реакция связи направлена в сторону, противоположную той, куда связь не дает двигаться материальной точке.
Принцип освобождения от связей: “Состояние движения (покоя) материальной точки не изменится, если действие связей заменить их реакциями”.
3.Связи с трением.
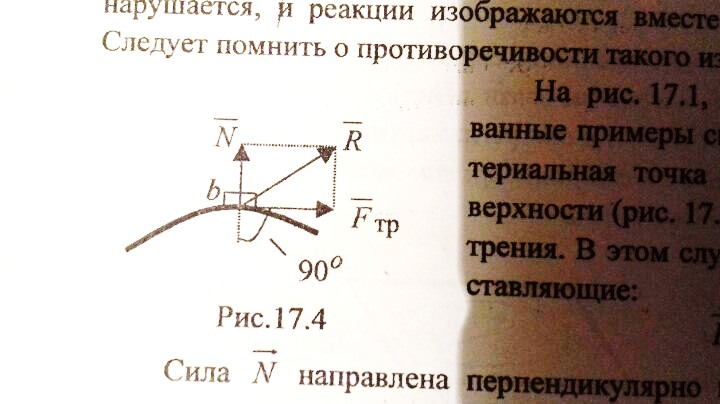
Если мат. точка находится на шероховатой поверхности, то будет присутствовать сила трения. В этом случае реакция связи имеет две составляющие 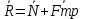 Сила Сила 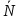 направлена перпендикулярно поверхности и называется нормальной составляющей реакции. Сила трения направлена перпендикулярно поверхности и называется нормальной составляющей реакции. Сила трения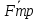 лежит в касательной плоскости, и ее модуль определяется законом Кулона: лежит в касательной плоскости, и ее модуль определяется законом Кулона: 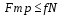 где f- коэффициент трения скольжения. Знак равенства в этой формуле следует поставить в момент начала движения где f- коэффициент трения скольжения. Знак равенства в этой формуле следует поставить в момент начала движения
4.Реальные и абстрактные механические задачи
В теоретических выкладках связи, наложенные на точку, не учитываются, и задачи решаются в несколько абстрактной форме. Однако большинство реальных задач на практике возникает именно для несвободных точек со связями.
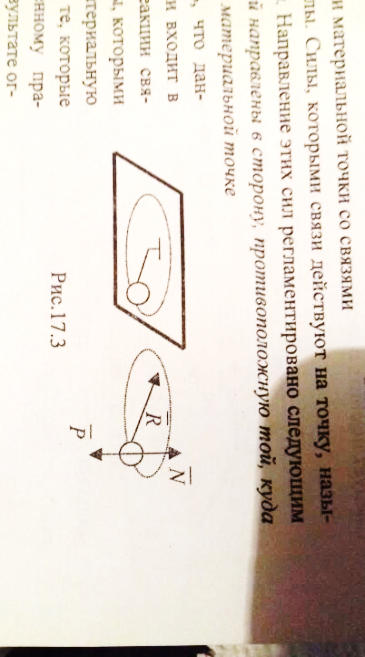
Переход от реальных задач практики к абстрактным теоретическим задачам со свободными точками осуществляется следующим образом. Пусть имеем реальную задачу со связями о движении шарика по плоскости (рис.). Заменим действие связей реакциями (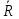 -реакция нити. -реакция нити. 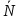 реакция плоскости). В результате получаем следующую абстрактную задачу: шарик движется по окружности под действием сил реакция плоскости). В результате получаем следующую абстрактную задачу: шарик движется по окружности под действием сил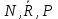 (сила (сила 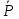 - вес шарика).Здесь точка свободна от связей и присутствуют только силы.На рисунках где изображены связи, не следует изображать реакции этих связей, и для абстрактных задач по возможности лучше делать новый рисунок. - вес шарика).Здесь точка свободна от связей и присутствуют только силы.На рисунках где изображены связи, не следует изображать реакции этих связей, и для абстрактных задач по возможности лучше делать новый рисунок.
5.Принцип равенства действия и противодейстия
Мат. Точка может взаимодействовать не только со связями,но и с другими материальными точками.Это взаимодействие регламентировано принципом равенства действия и противодействия. Две мат. Точки действуют друг на друга силами, равным по величине и противоположно направленными.
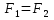
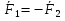
На мат. точку дейст-ют силы,кот-ые можно отнести к двум классам. К первому классу следует отнести силы,возникающие в результате взаимодействия рассматриваемой точки с другими мат.т.(активные)Их действие регламентировано принципом равенства действия и противодействия.Силы второго класса появляются в результате применения освобождения от связей.(пассивные силы)
6.Принцип независимости действия сил
Путь мат.т.b движется ,которая после применения принципа освобождения от связей стала свободной. Вместе с актив-ми силами реакции связей образуют систему сил 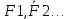 Вводится вектор Вводится вектор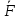 ,равный сумме всех действующих на точку сил ,равный сумме всех действующих на точку сил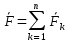 Движ-ие мат.т.( в частности, покой) не изменится, если систему сил Движ-ие мат.т.( в частности, покой) не изменится, если систему сил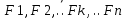 заменить заменить 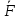 . Введенный принцип означает, что действие силы . Введенный принцип означает, что действие силы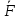 равно действию всей системы сил. Поэтому эту силу определенную равенством называют равнодействующей системы сил, действующих на мат.т. равно действию всей системы сил. Поэтому эту силу определенную равенством называют равнодействующей системы сил, действующих на мат.т.
7.Второй закон Ньютона:
“Сила, действующая на материальную точку, вызывает ее ускорение, пропорциональное вектору силы”. Второй закон Ньютона говорит о том, что вектор ускорения параллелен( пропорционален) вектору силы. Условие параллельности векторов можем записать в виде m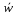 = = 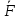 . Здесь коэффициент пропорциональности m есть масса точки. 2З.Н. справедлив в инерциальных системах отсчета. Принцип инерции: если на материальную точку не действуют силы, то она движется прямолинейно и равномерно . Здесь коэффициент пропорциональности m есть масса точки. 2З.Н. справедлив в инерциальных системах отсчета. Принцип инерции: если на материальную точку не действуют силы, то она движется прямолинейно и равномерно
(11)Уравнения динамики и статики материальной точки
|
 Скачать 2.59 Mb.
Скачать 2.59 Mb.







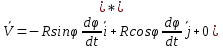 . Рассмотрим выражение
. Рассмотрим выражение 
















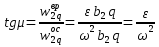 . Величина угла наклона вектора ускорения любой точки к отрезку, соединяющему эту точку с мгновенным центром ускорений, для всех точек плоской фигуры одинакова.
. Величина угла наклона вектора ускорения любой точки к отрезку, соединяющему эту точку с мгновенным центром ускорений, для всех точек плоской фигуры одинакова.



