Математика. Задачи к экзамену.. Задача Найти 5A 3B 2C, Найти 3A 2B 4C, Найти a 12E, Найти 4A 7B, Найти 5A 4B
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Задачи к экзамену по математике для студентов 1 курса ФМА 1 семестр Раздел 1: линейная алгебра. Задача 1.
Задача 2. Вычислить определитель матрицы: 1.А= 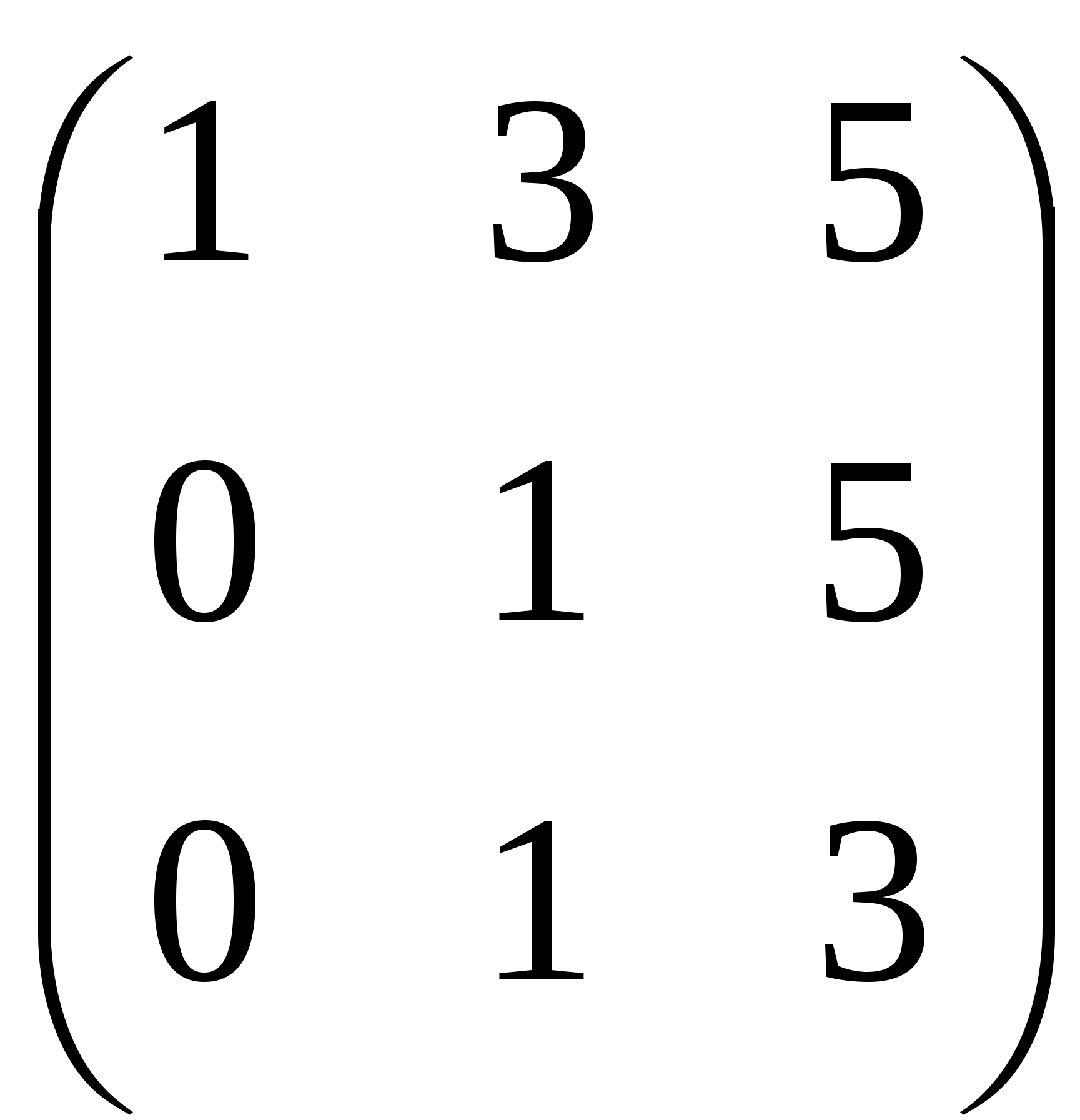 2. 2.  3. 3. 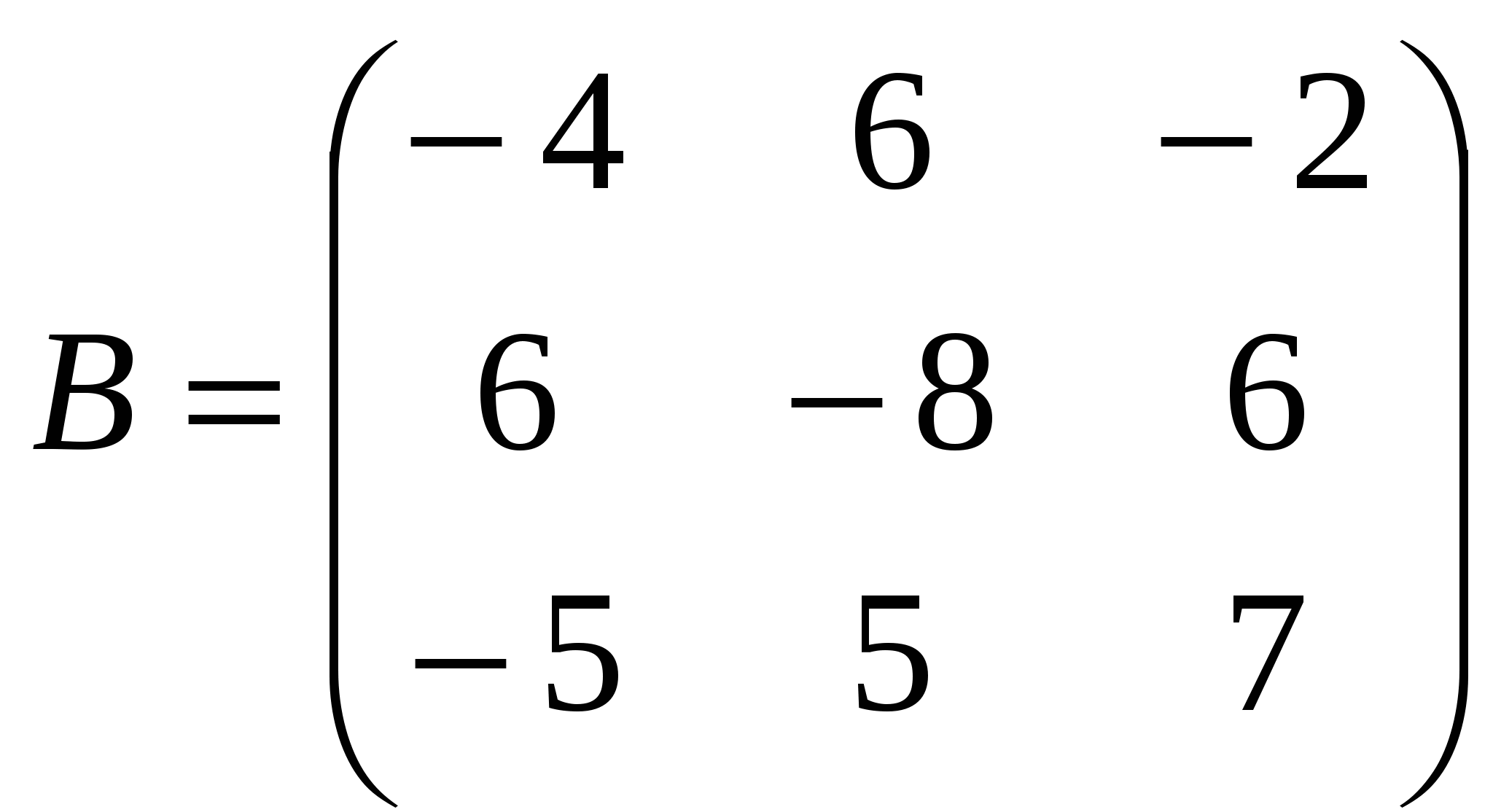 4. 4. 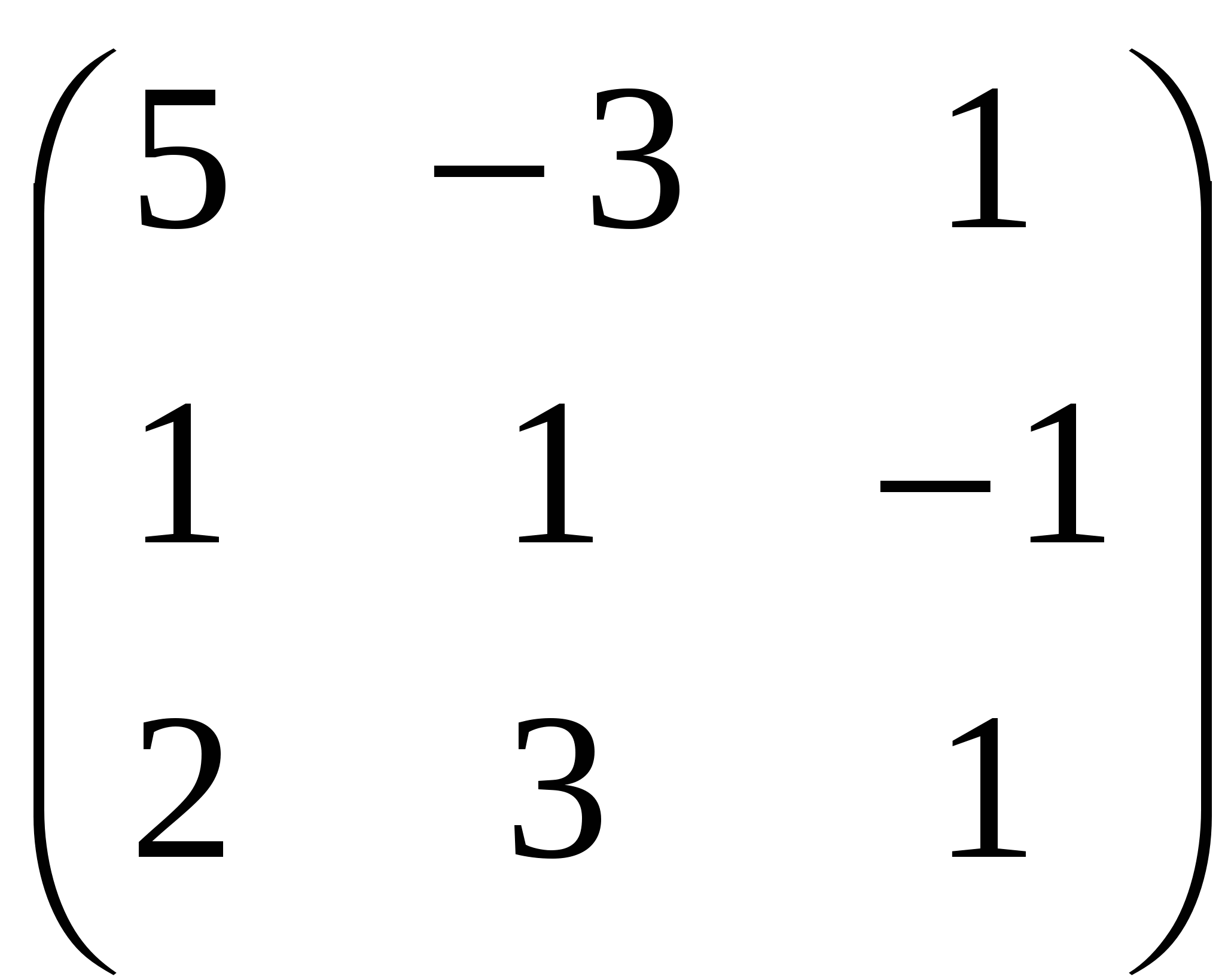 5. 5.  . .Задача 3. Найти произведение матриц: 1.  . .Задача 4. Вычислить обратную матрицу: 1. 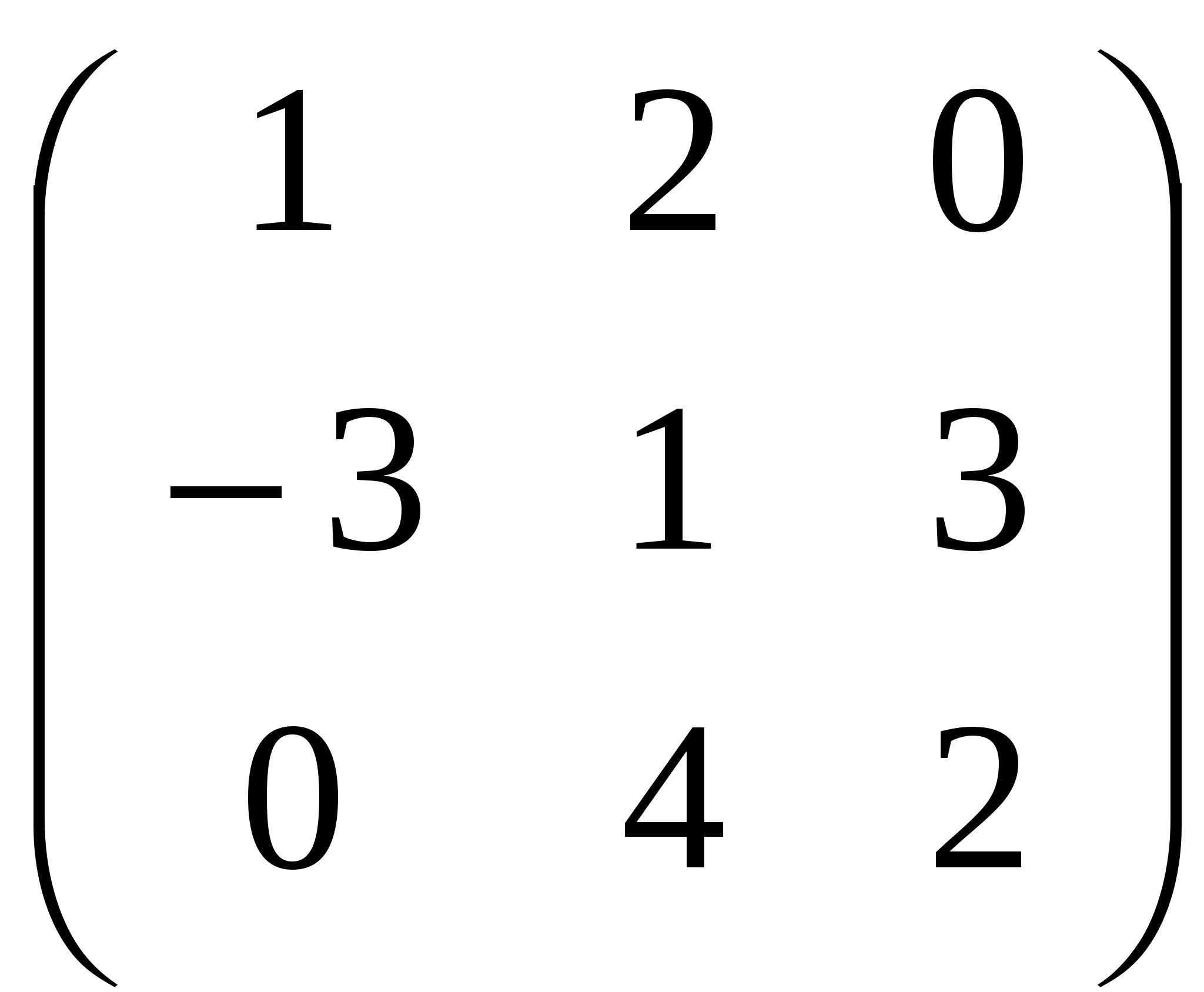 . .Раздел 2: векторная алгебра. Задача 1. Написать разложение вектора 1. 2. 3. 4. 5. Задача 2. Коллинеарны ли векторы 1. 2. 3. 4. 5. Задача 3. Найти косинус угла между векторами 1. 2. 3. 4. 5. Задача 4. Вычислить площадь параллелограмма, построенного на векторах 1. 2. 3. 4. 5. Задача 5. Компланарны ли векторы 1. 2. 3. 4. 5. Задача 6. Вычислить объем тетраэдра с вершинами в точках 1. 2. 3. 4. 5. Раздел 3: аналитическая геометрия в пространстве. Задача 1. Найти расстояние от точки 1. 2. 3. 4. 5. Задача 2. Написать уравнение плоскости, проходящей через точку 1. 2. 3. 4. 5. Задача 3. Написать канонические уравнения прямой. 1. 2. 3. 4. 5. Задача 4. Найти точку пересечения прямой и плоскости. 1. 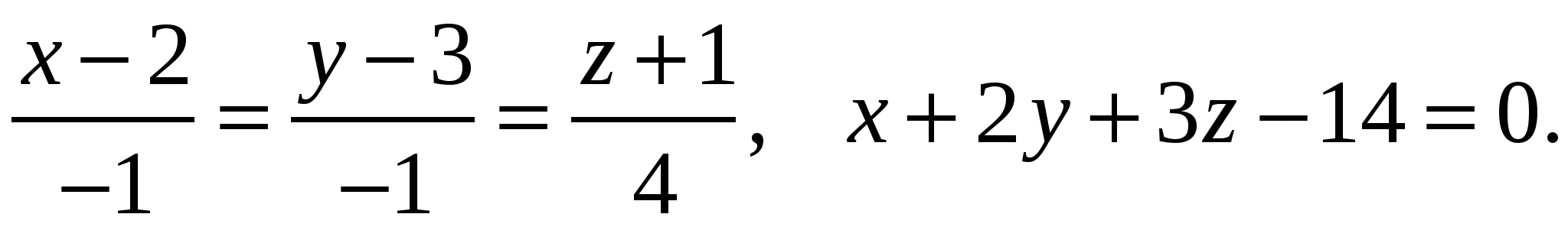 2. 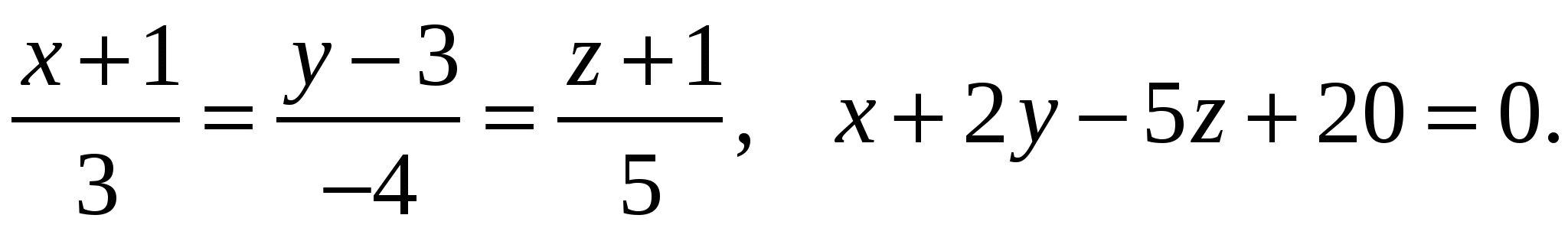 3. 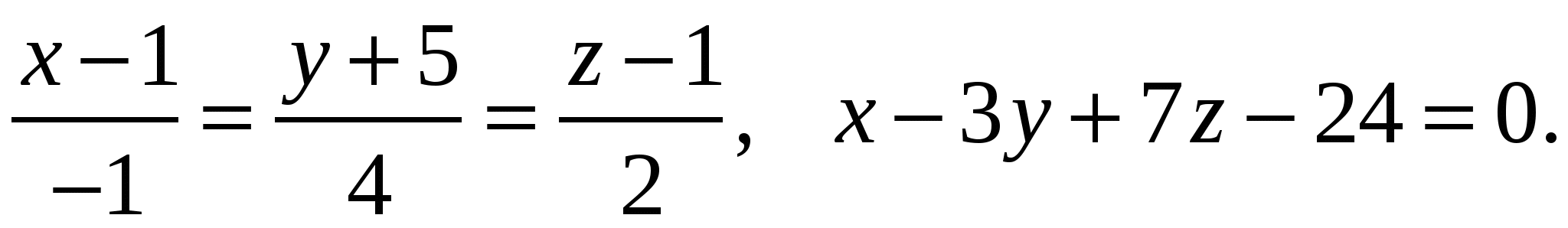 4.  5. 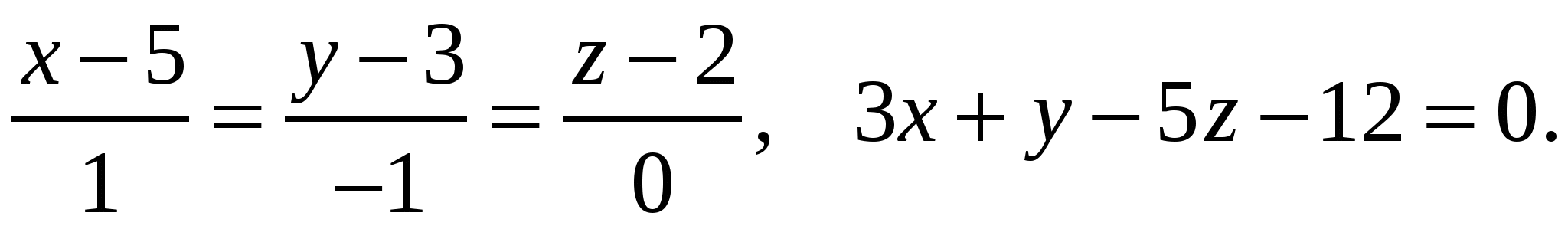 Раздел 4: аналитическая геометрия на плоскости. 1. Составить уравнение прямой, проходящей через точки А(1,-3) и В(2,-1). 2. Составить уравнение прямой, проходящей через точки А(1,3) и В(2,2). 3.Определить площадь треугольника, образованного прямой y = - 0,5x + 2 с осями координат 4. В треугольнике АВС, где т. А(4,-1), т. В(2,3), т. С(-4,-3), написать уравнение медианы, проведенной из т. А. 5. В треугольнике АВС, где т. А(-13,3), т. В(-1,-2), т. С(2,2), написать уравнение высоты проведённой из точки А. 6. В треугольнике АВС, где т. А(0,4), т. В(2,-6), т. С(-4,2), написать уравнение средней линии, параллельной ВС. 7. Найти точку пересечения диагоналей четырёхугольника АВСД, если А(0,6),В(7,12),С(6,2), Д(2,2). 8. Даны вершины треугольника АВС: А(-3, 1), В(0, 4), С(2, 5). Написать уравнение высоты, проведенной из вершины С к стороне АВ. 9. Стороны треугольника АВС заданы уравнениями: x+y=2 (AB), 2x-y=-2 (AC), x-2y=2 (BC). Написать уравнение высоты, проведенной из вершины А к стороне ВС. 10. Даны вершины треугольника АВС: А(4, -2), В(3, -1), С(2, 6). Написать уравнение средней линии ΔАВС, параллельной стороне АС. 11. Стороны треугольника АВС заданы уравнениями:x+y-3=0 (AB), y-2x=0 (AC), x-y-1=0 (BC). Написать уравнение прямой, проходящей через вершину А параллельно стороне ВС. 12. Даны вершины четырехугольника A(0, 6), B(7,12), C(6, 2), D(2, 2). Найти точку пересечения его диагоналей. 13. Даны вершины треугольника АВС: А(0, 4), В(-3, 2), С(2, 6). Написать уравнение медианы, проведенной из точки В. 14. Даны вершины треугольника АВС: А(2, 4), В(-2, 5), С(-1, 2). Написать уравнение высоты, проведенной из вершины А к стороне ВС. 15. Даны вершины трапеции A(-2,-3), B(-3, 1), C(7, 7), D(3, 0). Написать уравнение средней линии трапеции. 16. В треугольнике MNP написать уравнение медианы, проведенной из вершины М, если известно, что М(4, -1), N(2, 3), P(-4, -2). 17. Стороны треугольника лежат на прямых:x-y=-2 (AB), x+y=1 (BC), x-2y=1 (AC). Написать уравнение высоты, опущенной из вершины В на сторону АС. Раздел 5. Пределы. Непрерывность функции. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления 1. 1. 6. 11. 2. 16. 20. 24. 28. 31. 3. 35. 40. 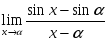 44. 44.45. 4. 47. 51. 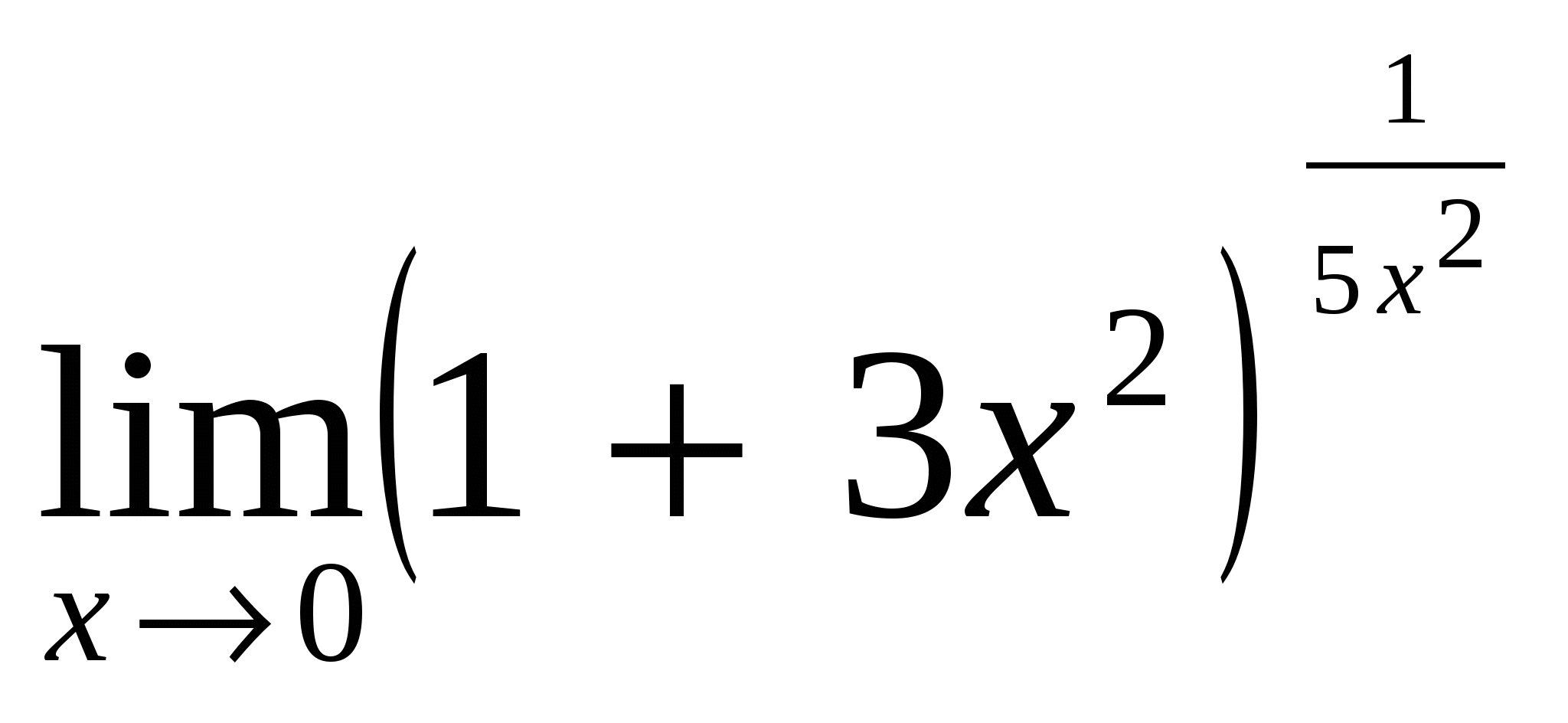 53. 53.55. 5. 60. 63 64. 68. 70. 6. Найти точки разрыва функции и установить характер разрыва. 1. у =  2. у = 2. у = 3. у = 3. у =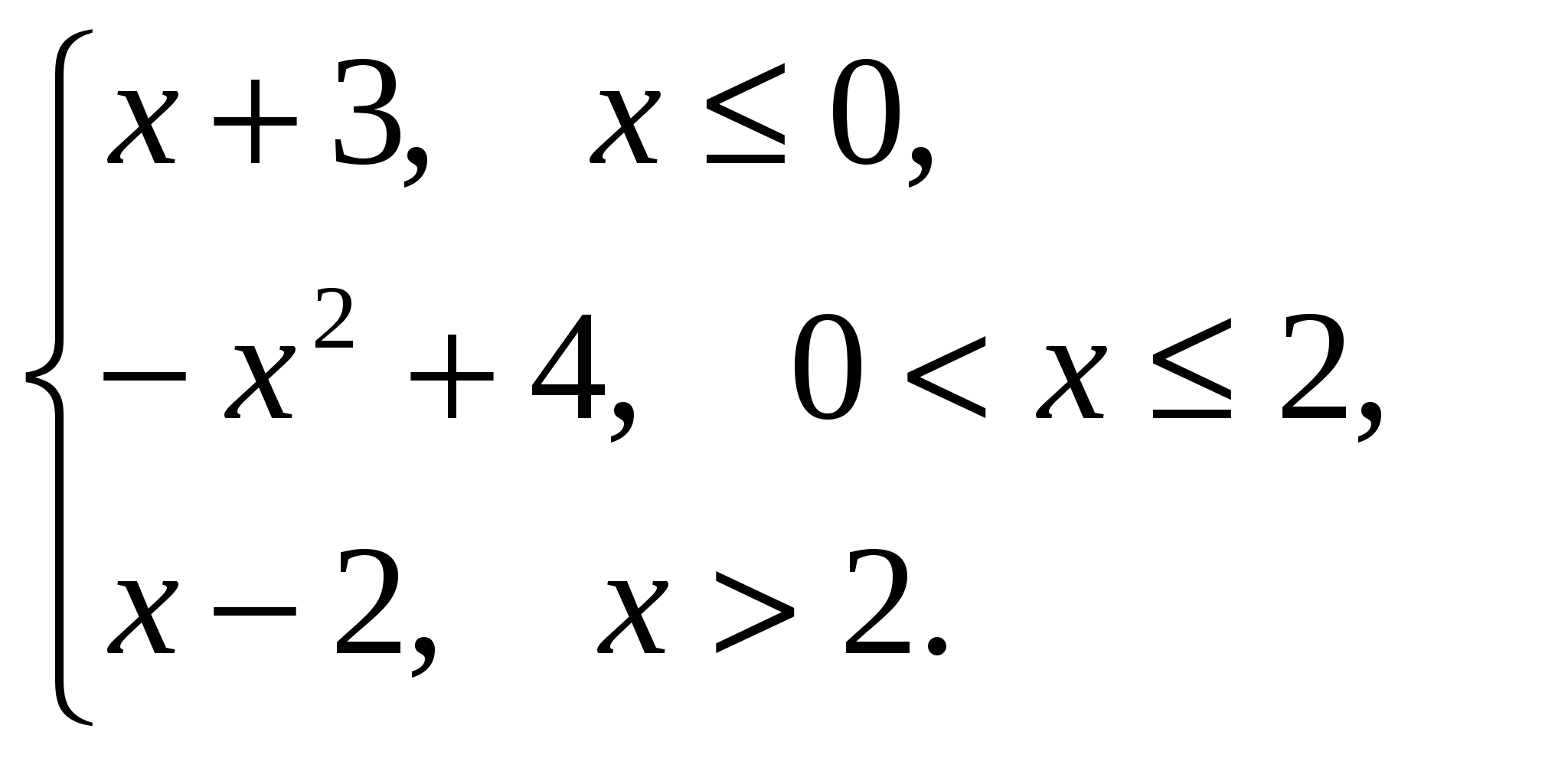 4. у = 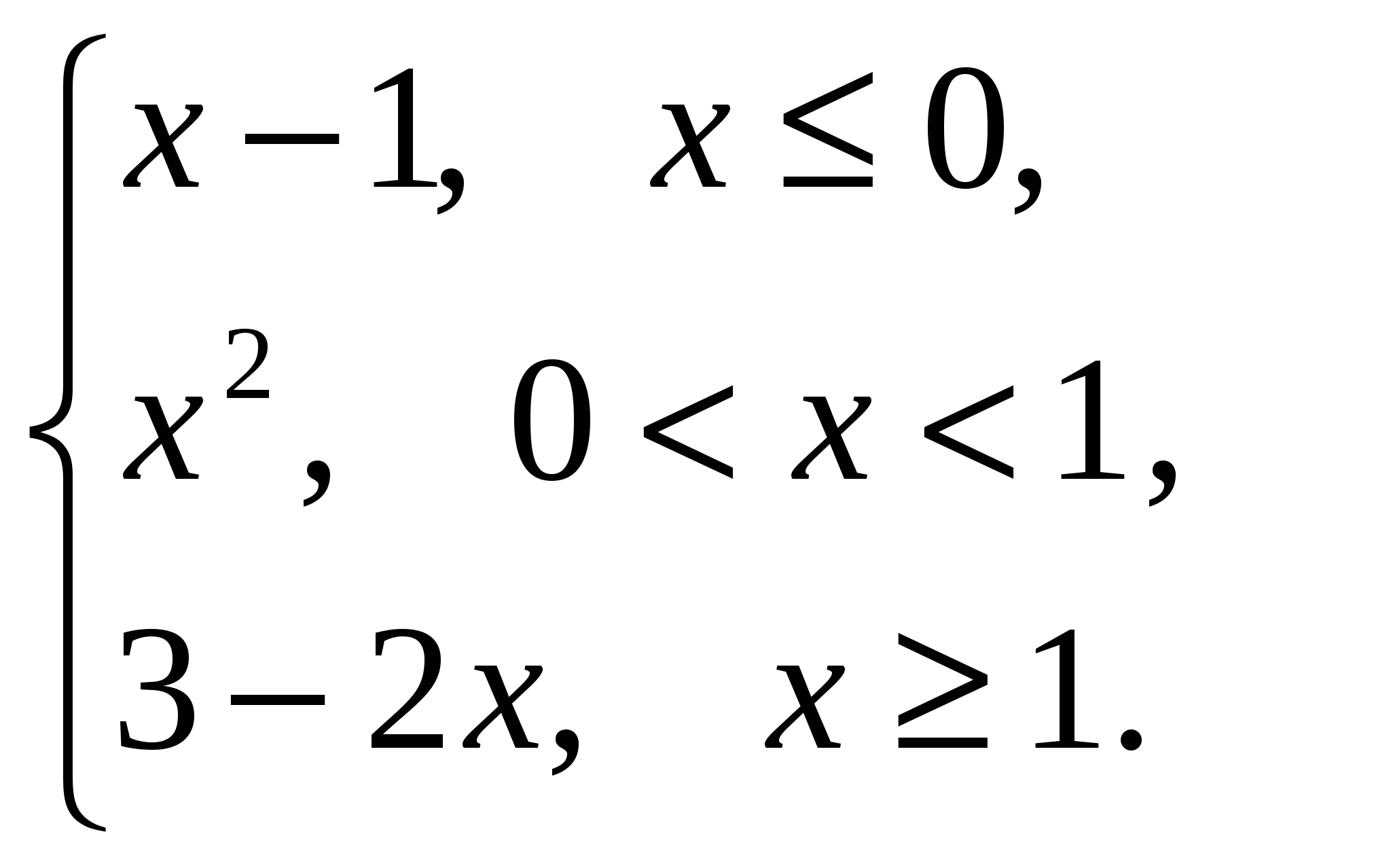 5. у = 5. у =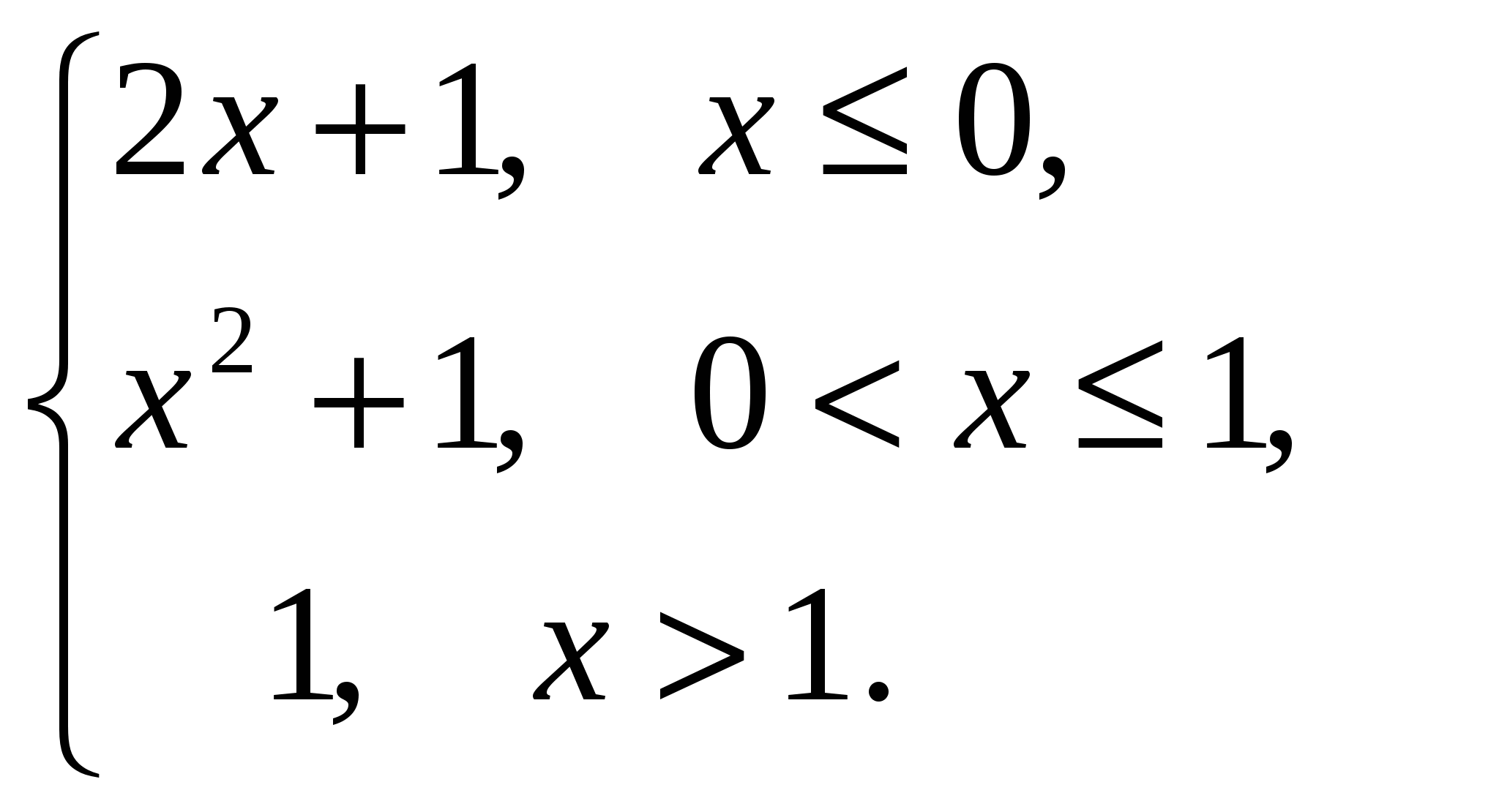 Раздел 6. Вычислить производные следующих функций: А. 1.a) 2. a) 3. a) 4. a) 5. a) 6. a) 7. a) 8. a) 9. a) 10. a) В. 1) 5) 10) 14) 17) 26) 29) 33) 36) 1) 41) 45) 49) 53) С. 1) 5) 9) 13) D. Найти производную параметрически заданной функции: 1)x=t-sint, y=2-cost; 2) x=e-t, y=arcsint; 3) x=sint+cost, y=sin2t; 4)x=tg2t, y=cos2t; 5) x=sint, y=ln(cost); 6) x=etsint, y=t+sint 7) 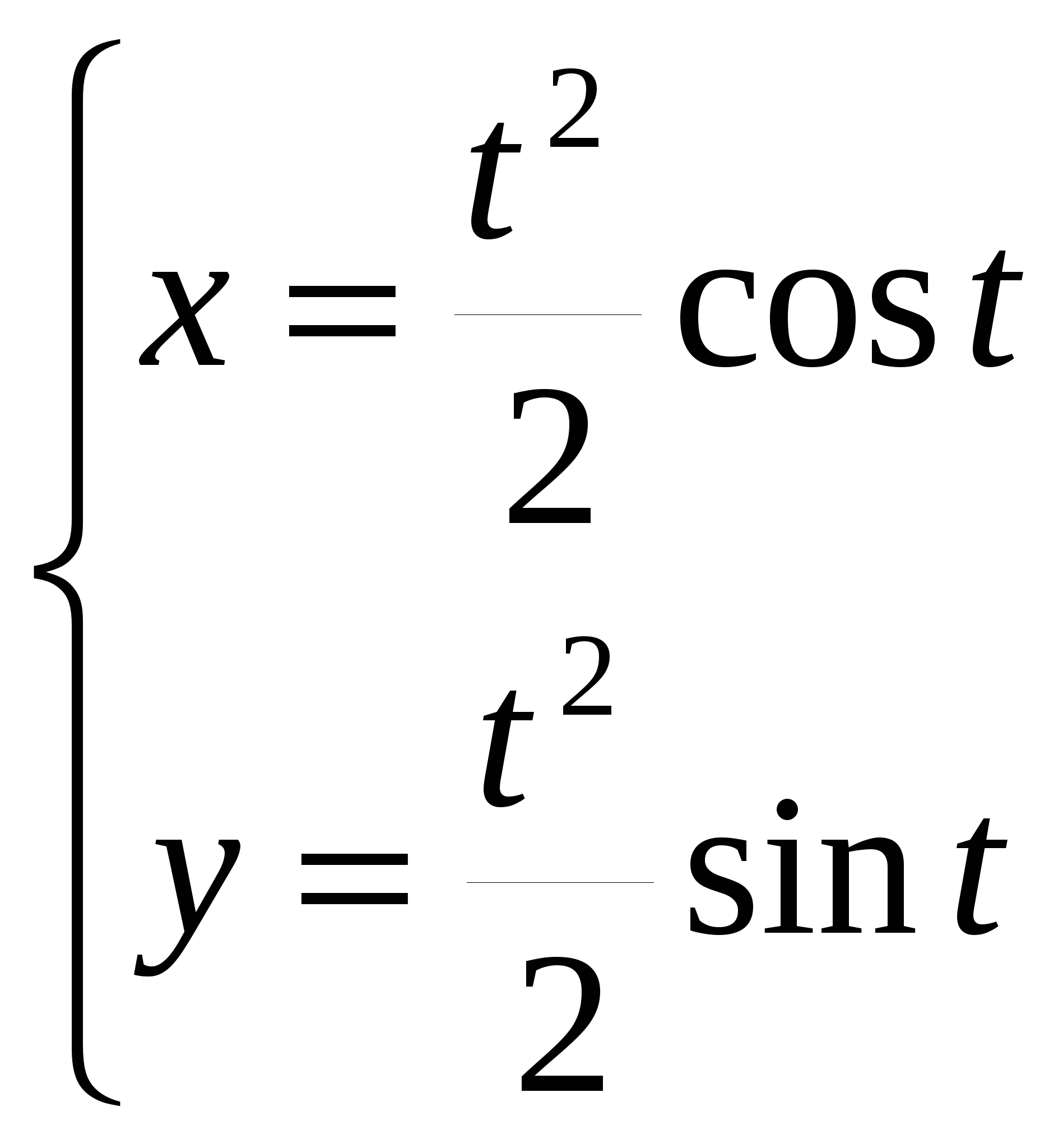 8) 8) 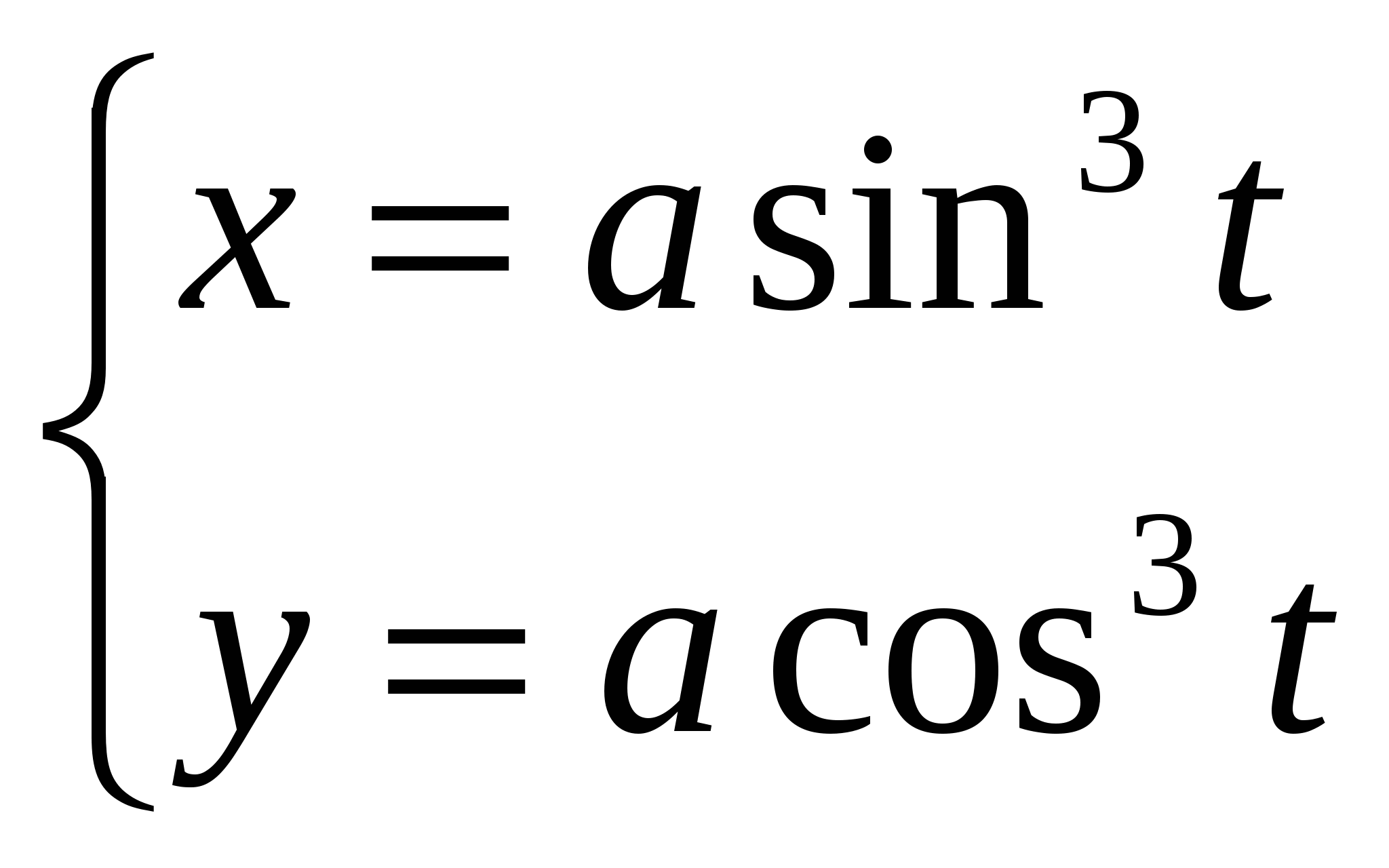 9) 9) 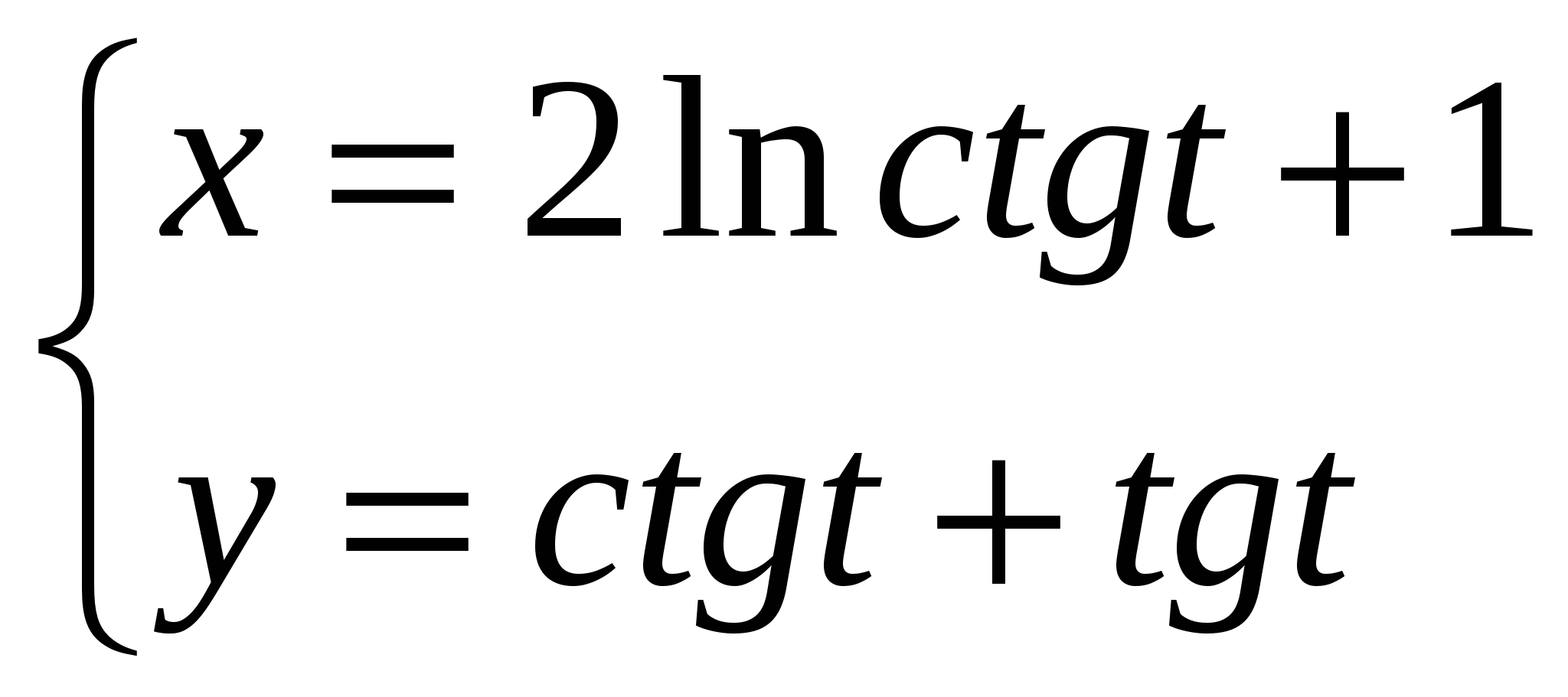 10) 10) 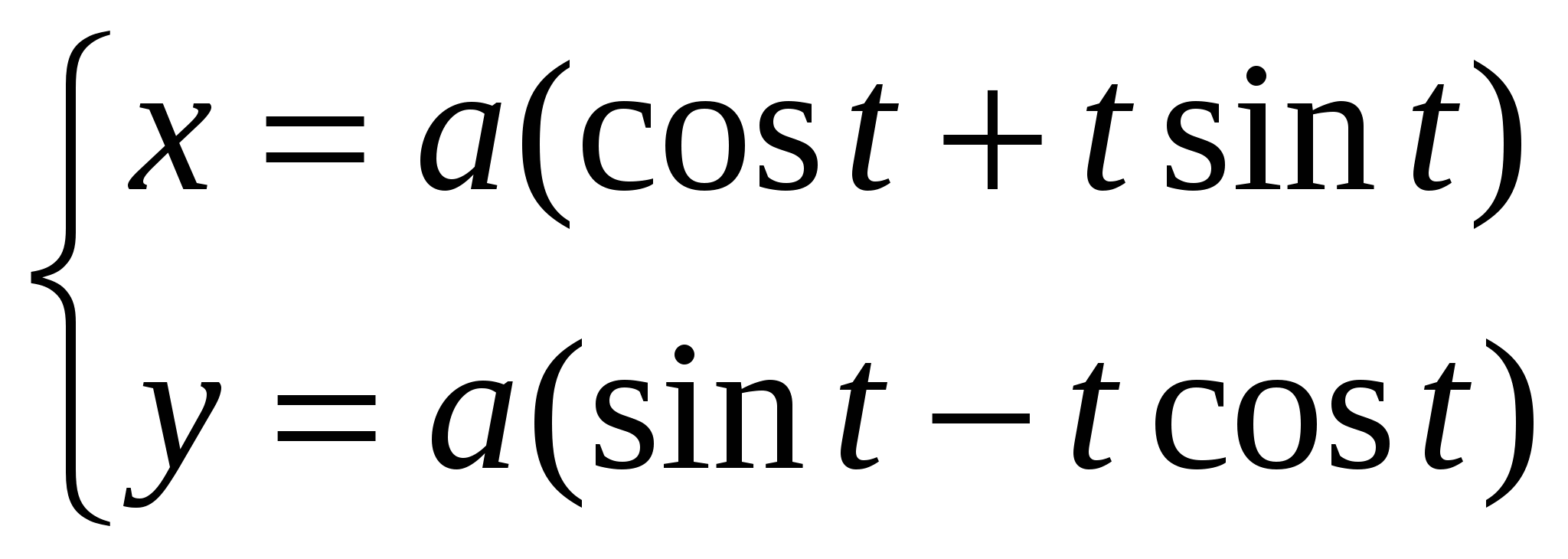 11) 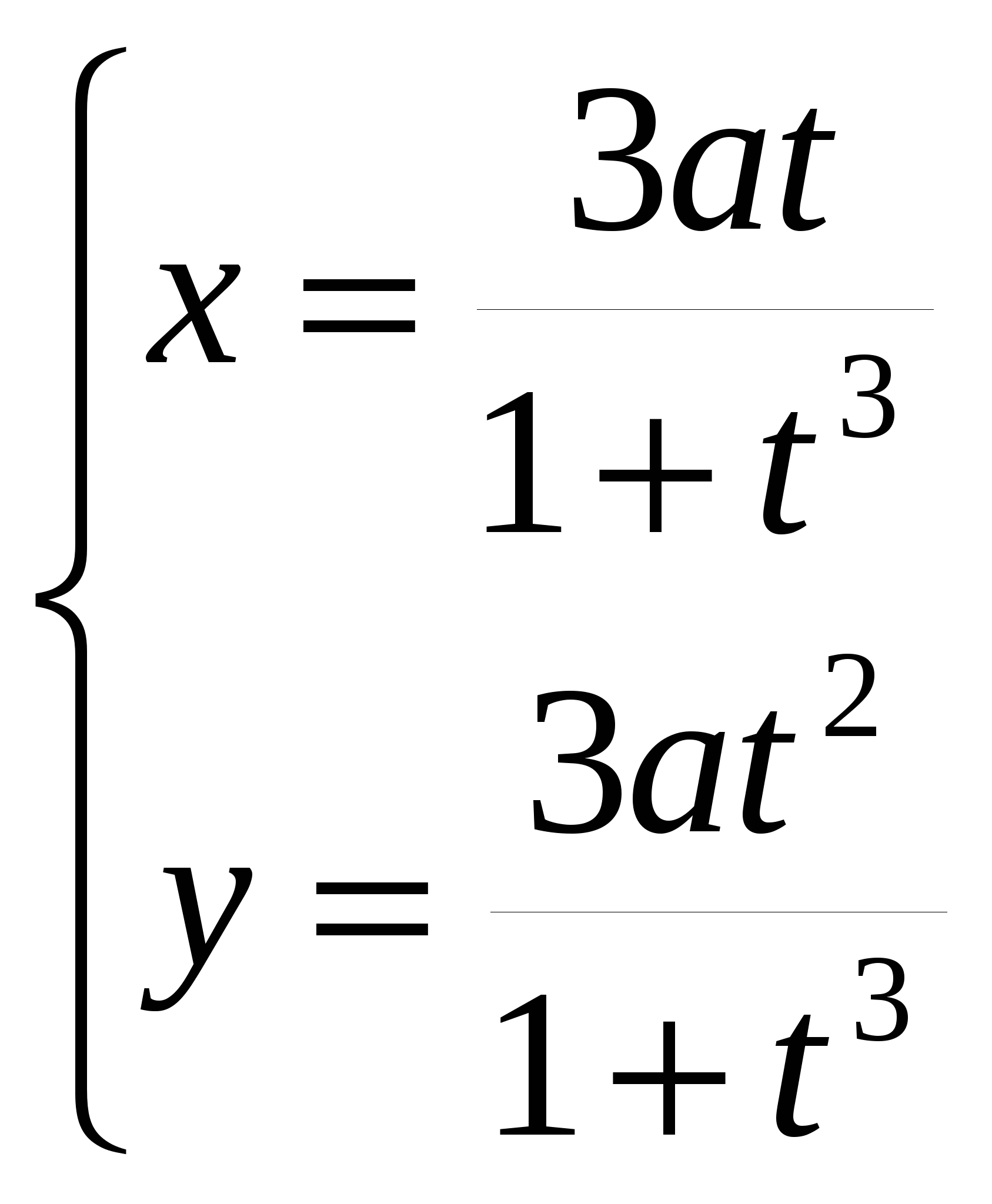 |

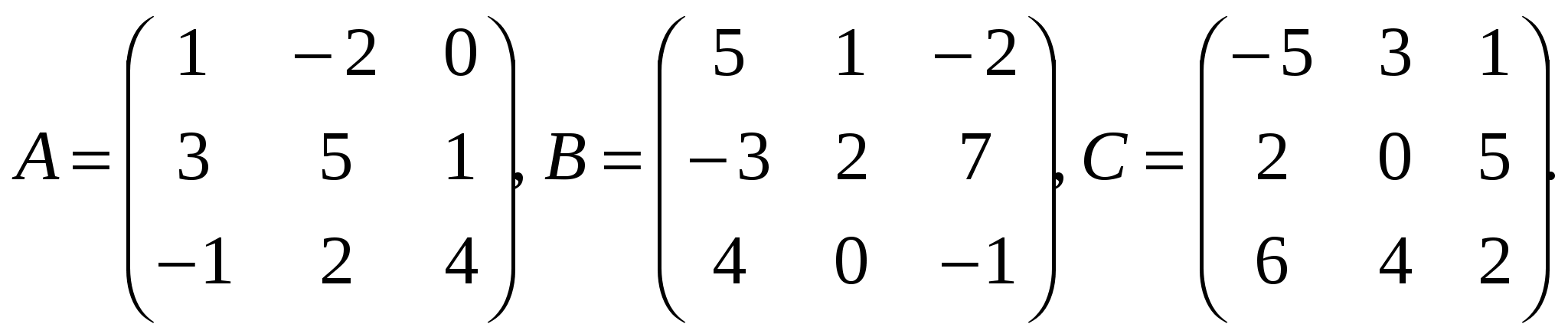

 .
.