Рейтинговая работа №1 Математика часть 1 Университет им. Витте. Кафедра Математика и информатика
 Скачать 251.1 Kb. Скачать 251.1 Kb.
|
 Кафедра ___Математика и информатика_________________________ Рейтинговая работа _______________________________________________ (домашняя творческая работа, расчетно-аналитическое задание, реферат, контрольная работа) по дисциплине _________________________________________________ Задание/вариант № 6 Тема* ______________________________________________________________ Выполнена обучающимся группы __________ __________________________________________________________________ (фамилия, имя, отчество) Преподаватель ____________________________________________________ (фамилия, имя, отчество) Москва – 2021 г. Содержание Задача 1 3 Задача 2 4 Задача 3 6 Задача 4 10 Список литературы 13 Вариант 6 Задача 1Даны матрицы  и число и число  . Найти матрицу . Найти матрицу  . .6)  , ,    Решение:  . .1) находим сначала произведение АВ Матрица A размера (3 на 2), а другая матрица Вразмера (2 на 3). Тогда произведение матриц A ⋅ B имеет размер (3 на 3). Умножаем: 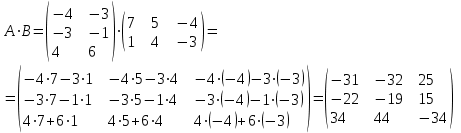 2) умножаем матрицу С на число (-2):  3) осталось сложить две полученные матрицы:  . .Вывод:  . .Задача 2Дана система линейных алгебраических уравнений Найти решение этой системы любым методом.  Решение: Применим матричный метод. Данное матричное уравнение имеет вид АХ = В, где   
Если определитель матрицы отличен от нуля, то решение системы ищем по формуле: Х = А-1В. Нужно сначала найти обратную матрицу А-1.
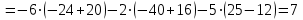 Получили определитель  7 ≠ 0, значит матрица А имеет обратную матрицу А-1. Найдем её по формуле: 7 ≠ 0, значит матрица А имеет обратную матрицу А-1. Найдем её по формуле:  = =  , , тут  - матрица из алгебраических дополнений элементов матрицы А. Найдем их: - матрица из алгебраических дополнений элементов матрицы А. Найдем их: 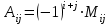 , где Міj – минор элемента аіj матрицы А. , где Міj – минор элемента аіj матрицы А.
 Искомая обратная матрица: Искомая обратная матрица:
Тогда решение найдем путем умножения этой матрицы на матрицу В:    
Ответ:  . .Задача 3Известны координаты (см. таблицу 1) в прямоугольной системе координат  трех точек трех точек  , являющихся вершинами треугольника. Изобразить треугольник , являющихся вершинами треугольника. Изобразить треугольник  в этой прямоугольной системе координат и найти: в этой прямоугольной системе координат и найти:3.1 координаты векторов 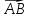 , , 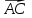 и их длины; и их длины;3.2 скалярное произведение векторов 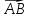 , , 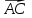 и угол и угол  между векторами между векторами 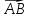 , , 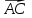 ; ;3.3 векторное произведение векторов 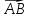 , , 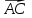 и площадь треугольника и площадь треугольника  3.4 значение параметра 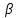 , при котором векторы , при котором векторы  и и  будут коллинеарны; будут коллинеарны;3.5 координаты точки  , делящей отрезок , делящей отрезок  в отношении в отношении  ; ;3.6 каноническое уравнение стороны  ; ;3.7 уравнение с угловым коэффициентом и угловой коэффициент прямой, проходящей через точку  параллельно прямой параллельно прямой  . .Таблица 1
Решение: Сделаем чертеж треугольника на координатной плоскости:    L 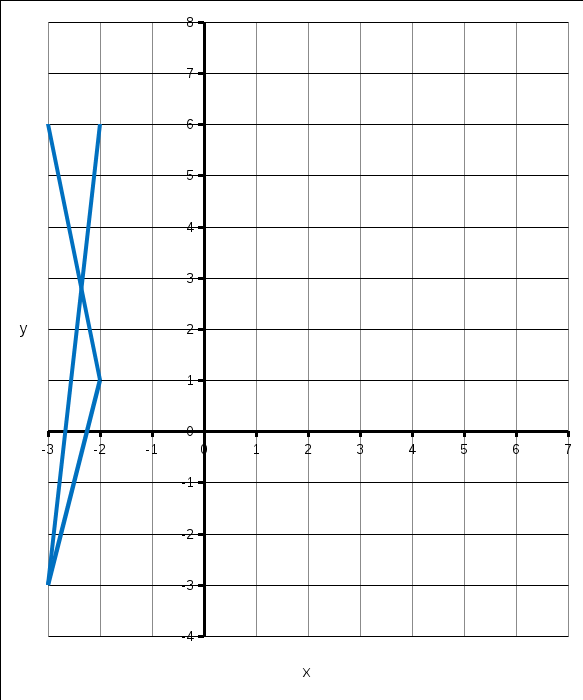 3.1. Координаты и длина 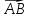 : :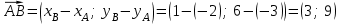  Координаты и длина 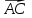 : : 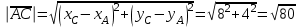 3.2 Найдем скалярное произведение векторов 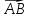 , , 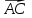 и угол и угол  между векторами между векторами 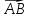 , , 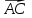     0,707) ≈ 45. 0,707) ≈ 45.3.3 найдем векторное произведение векторов 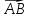 , , 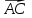 : : Площадь треугольника  равна половине от найденного значения: равна половине от найденного значения: 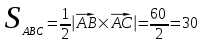 . .3.4 найдем значение параметра 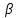 , при котором векторы , при котором векторы  и и  будут коллинеарны. будут коллинеарны. 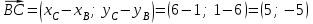 Векторы коллинеарны, если их координаты будут взаимно пропорциональны:      . .3.5 найдем координаты точки  , делящей отрезок , делящей отрезок  в отношении в отношении  , если , если 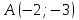 , ,  , т.е. , т.е. 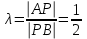 . .Координаты точки  : : 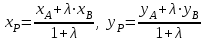 , т.е. , т.е.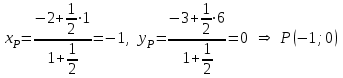 . .3.6 найдем каноническое уравнение стороны  . . 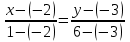   . . 3.7 найдем уравнение с угловым коэффициентом и угловой коэффициент прямой, проходящей через точку  параллельно прямой параллельно прямой  . .   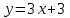 Тогда параллельная ей прямая имеет уравнение  , где при х = 6: у =1, т.е. , где при х = 6: у =1, т.е.  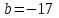  . Угловой коэффициент k = 3. . Угловой коэффициент k = 3.Задача 44) Известны координаты (см. таблицу 2) в прямоугольной системе координат  вершин пирамиды вершин пирамиды 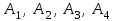 . .4.1 найти смешанное произведение векторов  и объем пирамиды и объем пирамиды 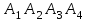 ; ;4.2 найти каноническое уравнение прямой  ; ;4.3 найти общее уравнение плоскости 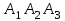 . .Таблица 2
Решение: 4.1. Сначала найдем координаты векторов А1А2, А1А3 и А1А4 .
Смешанное произведение векторов по заданным координатам ищем по формуле: Для 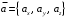 , , 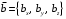 , ,  : :  , у нас: , у нас:
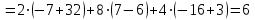 Модуль этого смешанного произведения 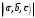 равен объему параллелепипеда, который построен на этих векторах равен объему параллелепипеда, который построен на этих векторах  и и 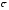 , при этом объем пирамиды равен 1/6 от объема всего параллелепипеда. , при этом объем пирамиды равен 1/6 от объема всего параллелепипеда.У нас объем пирамиды равен: V =  (ед3). (ед3).4.2 каноническое уравнение прямой  : :  , где A1(0,7,1), A2(2,-1,5) , подставляем координаты, получаем: , где A1(0,7,1), A2(2,-1,5) , подставляем координаты, получаем:   . .4.3. Уравнение плоскости 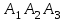 : :  (уравнение по трем точкам пространства) (уравнение по трем точкам пространства)
Это определитель 3-го порядка, раскроем его:
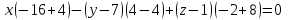  Упростим:  Сократим на (-6): 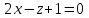 . .Ответ: 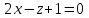 . .Список литературы1. Ильин, В.А. Линейная алгебра и аналитическая геометрия: Учебник / В.А. Ильин, Г.Д. Ким.. - М.: Проспект, 2012. - 400 c. 2. Ильин В.А., Позняк Э.Г., Аналитическая геометрия, М: Физматлит, 2017.-224 с. 3. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры: Учебник для вузов. – М.: Физматлит, 2005. – 304 с. 4. Канатников А.Н., Крищенко А.П., Аналитическая геометрия, М., Изд. МГТУ им. Н.Э. Баумана, 2015, - 336 с. 5. Кремер, Н.Ш. Линейная алгебра: Учебник и практикум / Н.Ш. Кремер, М.Н. Фридман. - Люберцы: Юрайт, 2016. - 306 c. 6. Письменный Д. Т. Конспект лекций по высшей математике: полный курс. - М.: Айрис-пресс, 2011. - 608 с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

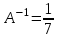
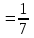
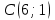

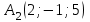
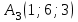
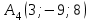
 =(
=(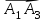 =(
=( =(
=(