рейтинговая работа. Рейтинговая работа. Кафедра Математика и информатика
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца. Г3,1=0, Г3,2=0, Г4,2=6, Г5,1=0, Г5,3=6 В результате сравнения мы получили 2 одинаковых максимальных Г=6. Это означает что алгоритм разветвляется, и мы должны рассмотреть все получившиеся варианты поочередно. Рассмотрим вариант Г4,2=6. Удалим из матрицы стоимости строку 4 и столбец 2, и присвоим элементу (2,4) значение бесконечности. Внесем в текущий ориентированный граф дугу (4,2).
В строке 5 и столбце 1 отсутствует элемент равный ∞. Присвоим элементу (5,1) значение бесконечности чтобы избежать преждевременного замыкания контура. Текущая нижняя граница=12. После того, как ранг матрицы становится равным двум, мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтенные элементы матрицы к нижней границе), и добавляем к маршруту коммивояжера дуги которым соответствуют нулевые элементы. НГр=12 Маршрут коммивояжера включает в себя дуги: (2, 5), (1, 4), (4, 2), (3, 1), (5, 3). Вернемся к возникшему у нас ветвлению и рассмотрим случай, при котором максимальное значение имеет Г5,3. Удалим из матрицы стоимости строку 3 и столбец 5. Внесем в текущий ориентированный граф дугу (5,3).
В строке 3 и столбце 2 отсутствует элемент равный ∞. Присвоим элементу (3,2) значение бесконечности чтобы избежать преждевременного замыкания контура. После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтенные элементы матрицы к нижней границе), и добавляем к маршруту коммивояжера дуги которым соответствуют нулевые элементы. НГр=12. Окончательно, маршрут коммивояжера включает в себя дуги: (2,5), (1,4), (5,3), (3,1), (4,2) Сам маршрут (начинаем с вершины 1): 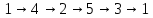 Длина этого кратчайшего маршрута равна 12. Задание 2. Найдите коэффициент при 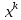 в разложении полинома: в разложении полинома: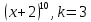 Решение. Используем формулу бинома Ньютона: 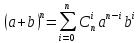 Здесь 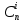 - число сочетаний без повторений из - число сочетаний без повторений из 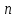 элементов по элементов по 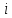 , рассчитывается по формуле: , рассчитывается по формуле: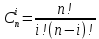 У нас 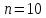 : :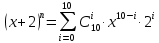 Коэффициент при 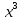 : значение : значение 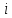 равно равно 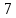 : :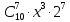 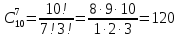 Коэффициент при 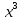 в разложении полинома в разложении полинома 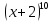 равен: равен: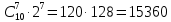 Ответ: 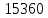 . . |
