рейтинговая работа. Рейтинговая работа. Кафедра Математика и информатика

• Название: Кафедра Математика и информатика
• Анкор: рейтинговая работа
• Дата: 02.09.2022
• Размер: 0.56 Mb.
• Имя файла: Рейтинговая работа.docx
• Тип: Документы; #659403
• страница: 4 из 6

11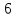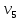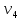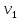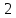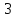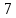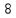





















14

9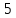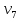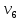








Остаются только две непостоянные вершины: 4 и 7. Очевидно, что метки для них обновить нельзя, ребро направлено от 4 к 7 вершине, а метка для 4 вершины имеет большее значение. Так что эти две вершины также можно считать постоянными.

Минимальные пути из вершины 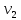во все другие вершины в ориентированном нагруженном графе (длины путей равны значениям меток):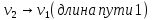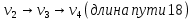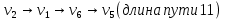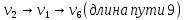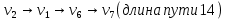













4. Комбинаторика. Применение графовых моделей.
Задание 1. Задана исходная матрица расстояний:

M	3	4	2	7
5	M	8	4	3
2	3	M	7	5
3	2	9	M	1
1	2	3	5	M

Решить задачу коммивояжёра.

Решение. Решение задачи происходит методом Литтла (частный случай метода ветвей и границ).

Матрица стоимости для графа, элементами которой являются веса соответствующих дуг (все элементы по диагонали матрицы приравниваем к бесконечности):

∞	3	4	2	7
5	∞	8	4	3
2	3	∞	7	5
3	2	9	∞	1
1	2	3	5	∞

Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.

	1	2	3	4	5
1	∞	1	2	0	5	2
2	2	∞	5	1	0	3
3	0	1	∞	5	3	2
4	2	1	8	∞	0	1
5	0	1	2	4	∞	1

То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.

	1	2	3	4	5
1	∞	0	0	0	5
2	2	∞	3	1	0
3	0	0	∞	5	3
4	2	0	6	∞	0
5	0	0	0	4	∞
	0	1	2	0	0

Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца.

Г_1,2=0, Г_1,3=0, Г_1,4=1, Г_2,5=1, Г_3,1=0, Г_3,2=0, Г_4,2=0, Г_4,5=0, Г_5,1=0, Г_5,2=0, Г_5,3=0

В результате сравнения мы получили 2 одинаковых максимальных Г=1. Это означает что алгоритм разветвляется, и мы должны рассмотреть все получившиеся варианты поочередно.
Рассмотрим вариант Г_1,4=1. Удалим из матрицы стоимости строку 1 и столбец 4. Внесем в текущий ориентированный граф дугу (1,4).

	1	2	3	5
2	2	∞	3	0
3	0	0	∞	3
4	2	0	6	0
5	0	0	0	∞

В строке 4 и столбце 1 отсутствует элемент равный ∞. Присвоим элементу (4,1) значение бесконечности, чтобы избежать преждевременного замыкания контура.
Текущая нижняя граница = 12.


Нижняя граница равна сумме всех вычтенных элементов в строках и столбцах. Итоговое значение нижней границы должно совпасть с длиной результирующего контура.


Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.

	1	2	3	5
2	2	∞	3	0
3	0	0	∞	3
4	∞	0	6	0
5	0	0	0	∞

То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.

	1	2	3	5
2	2	∞	3	0
3	0	0	∞	3
4	∞	0	6	0
5	0	0	0	∞