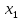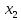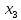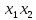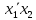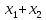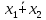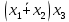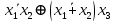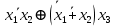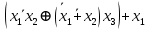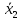рейтинговая работа. Рейтинговая работа. Кафедра Математика и информатика
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
 Кафедра ___Математика и информатика_________________________ Рейтинговая работа по дисциплине ___________Дискретная математика________________ Задание/вариант № ____2________ Выполнена__________Пыховым Николаем Владимировичем___________ (фамилия, имя, отчество) Преподаватель _________Калинин Владимир Михайлович_____________ (фамилия, имя, отчество) Москва 2019 г. Вариант №2 Выполнение операций над множествами. Задание 1. Построить выражения над множествами 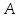 (круг), (круг), 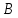 (квадрат) и (квадрат) и 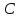 (треугольник), которым соответствуют заштрихованные области на заданных диаграммах Эйлера-Венна. (треугольник), которым соответствуют заштрихованные области на заданных диаграммах Эйлера-Венна. Решение. Заштрихованная область состоит из двух частей (непересекающихся множеств): 1) Общая часть всех трёх множеств 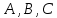 - это пересечение этих множеств: - это пересечение этих множеств: 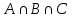 2) Часть множества 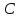 (треугольника), элементы которой не принадлежат ни множеству (треугольника), элементы которой не принадлежат ни множеству 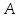 (кругу), ни множеству (кругу), ни множеству 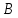 (квадрату). Значит эта область – разность множеств (квадрату). Значит эта область – разность множеств 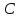 и объединения множеств и объединения множеств 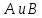 : :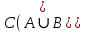 Объединяем эти две части: 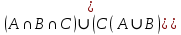 Ответ: 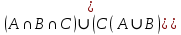 Задание 2. Упростить выражение 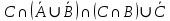 . .Решение. Операция пересечения имеет больший приоритет, чем операция объединения, поэтому вставляем скобки следующим образом: 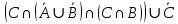 Применяем закон ассоциативности к операции пересечения и вставляем ещё скобки: 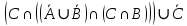 Используем закон дистрибутивности объединения относительно пересечения: 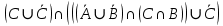 Используем закон 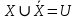 (универсальное множество): (универсальное множество):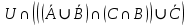 Используем закон 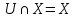 : :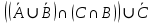 Используем закон дистрибутивности объединения относительно пересечения: 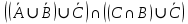 Упрощаем 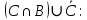 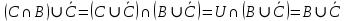 Получаем: 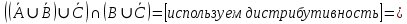 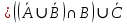 Упрощаем 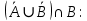 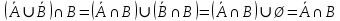 Окончательно, получаем: 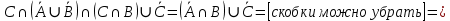 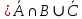 Ответ: 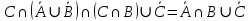 2. Выполнение операций алгебры логики Задание 1. Представить в СКНФ функцию 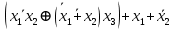 . .Решение. Сначала составляем последовательно таблицу истинности для заданной функции. Учитывается, что отрицание меняет истинность, конъюнкция (логическое умножение, знак опущен) истинна только в том случае, когда оба операнда истины, дизъюнкция (логическое сложение) ложна только в том случае, когда оба операнда ложны, строгая дизъюнкция 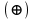 истинна только в том случае, когда оба операнда имеют разное логическое значение. истинна только в том случае, когда оба операнда имеют разное логическое значение.
Продолжение таблицы истинности:
Каждый набор переменных, на котором функция принимает значение 0, определяет член в совершенной конъюнктивной нормальной форме (СКНФ), причём переменная входит в этот член с отрицанием, если в наборе она имеет значение 1. В нашем случае СКНФ содержит два члена. СКНФ: 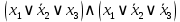 Ответ: 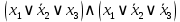 Задание 2. Пусть даны высказывания 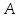 :=«существует бюджетный дефицит» и :=«существует бюджетный дефицит» и 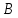 :=«имеется превышение бюджетных расходов над бюджетными доходами». Записать в словесной форме высказывание :=«имеется превышение бюджетных расходов над бюджетными доходами». Записать в словесной форме высказывание 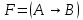 . .Решение. Заданное высказывание – импликация, или логическое следование: из 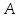 следует следует 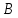 . В словесной форме реализуется оборотом ”Если A, то B”: “Если существует бюджетный дефицит, то имеется превышение бюджетных расходов над бюджетными доходами”. . В словесной форме реализуется оборотом ”Если A, то B”: “Если существует бюджетный дефицит, то имеется превышение бюджетных расходов над бюджетными доходами”.Ответ: “Если существует бюджетный дефицит, то имеется превышение бюджетных расходов над бюджетными доходами”. 3. Решение задач по теории графов Задание 1. Задана таблица смежности неориентированного графа. Определить сумму степеней вершин в данном графе. 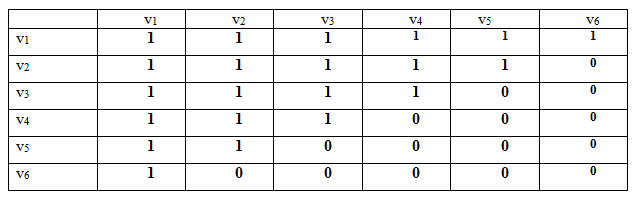 Решение. В таблице смежности неориентированного графа единица, стоящая в 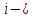 той строке и той строке и 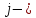 том столбце означает то, что вершины том столбце означает то, что вершины 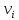 и и 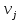 смежные (соединены ребром). Если единица стоит в смежные (соединены ребром). Если единица стоит в 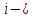 той строке и той строке и 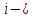 том столбце, то при вершине том столбце, то при вершине 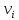 имеется петля. Запишем матрицу смежности по заданной таблице: имеется петля. Запишем матрицу смежности по заданной таблице: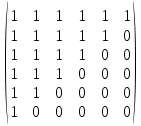 По главной диагонали этой матрицы стоит 3 единицы, значит число петель в графе равно 3. Это петли при вершинах 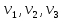 . . Построим граф по заданной таблице смежности.     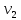 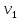             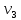     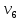     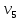 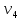 Степень вершины 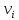 – число рёбер, включающих эту вершину, степень равна числу единиц в – число рёбер, включающих эту вершину, степень равна числу единиц в 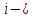 той строке или той строке или 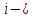 том столбце матрице смежности. Петлю нужно учитывать 2 раза, т.е. единицы по главной диагонали учитываем дважды. Степени вершин: том столбце матрице смежности. Петлю нужно учитывать 2 раза, т.е. единицы по главной диагонали учитываем дважды. Степени вершин: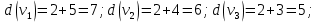 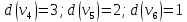 Сумма степеней вершин в заданном графе: 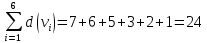 Другой способ основывается на том, что сумма степеней всех вершин равна удвоенному числу всех рёбер графа. По изображению графа видим, что рёбер в графе (включая петли) 12, получаем: 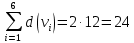 Ответ: сумма степеней вершин равна 24. Задание 2. Найти минимальные пути из вершины 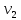 во все другие вершины в ориентированном нагруженном графе, изображённом на рисунке, с применением алгоритма Дейкстры. во все другие вершины в ориентированном нагруженном графе, изображённом на рисунке, с применением алгоритма Дейкстры.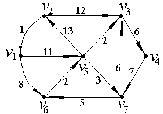 Решение. Помечаем метками (в рамке - значение текущего минимального расстояния от вершины 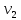 ) все вершины: для вершины ) все вершины: для вершины 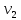 – нулевая метка, для остальных – бесконечность: – нулевая метка, для остальных – бесконечность:     ∞ |