Курсовая ОТС. Курсовая работа ОТС Усков БРМ1801. Кафедра общей теории связи курсовая работа по дисциплине
 Скачать 1.04 Mb. Скачать 1.04 Mb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ Ордена Трудового Красного Знамени федеральное государственное образовательное бюджетное учреждение высшего образования Московский технический университет связи и информатики (МТУСИ) КАФЕДРА ОБЩЕЙ ТЕОРИИ СВЯЗИ КУРСОВАЯ РАБОТА ПО ДИСЦИПЛИНЕ: Общая теория связи. Выполнил: Усков Семен Сергеевич Вариант: 28 Группа: БРМ1801 Преподаватель: Поборчая Н.Е. Москва 2020 Оглавление: Индивидуальное задание 3 Структурная схема 3-4 Временные диаграммы 4-6 Пункт 1 6-7 Пункт 2 7-8 Пункт 3 8-9 Пункт 4 9-10 Пункт 5 11-12 Пункт 6 12-13 Пункт 7 13-14 Пункт 8 14-15 Пункт 9 15-16 Пункт 10 17 Пункт 11 17-18 Список литературы 19 Индивидуальное задание. Вариант: 28. Таблица 1. Исходные данные.
Где: PA=σ2A – мощность (дисперсия) сообщения; β – показатель затухания функции корреляции; L – число уровней квантования; G0 – постоянная энергетического спектра шума НКС; h02 – отношение сигнал/шум (ОСШ) по мощности на входе детектора; АМ – амплитудная модуляция; НП – некогерентный приём. Структурная схема системы электросвязи. 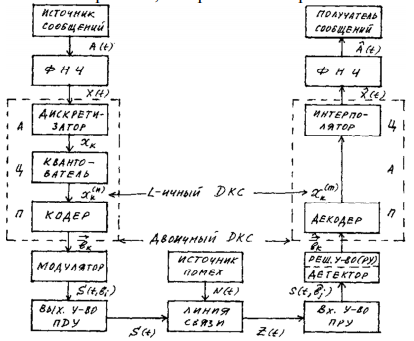 Рисунок 1 – Структурная схема. Назначение отдельных элементов схемы: Источник сообщения – некоторый объект или система, информацию о состоянии которой необходимо передать; A(t) – сообщение, несущее в себе новую информацию о состоянии источника; ФНЧ – ограничивает спектр сообщения некоторой частотой FB; АЦП – аналогово-цифровой преобразователь, в состав которого входят: 1) Дискретизатор – устройство, представляющее отклик ФНЧ в виде отсчётов xk; 2) Квантователь – устройство, преобразующее отсчёты в квантованные уровни xk(n); k=0,1,2..; n=0,L; L – число уровней квантования; 3) Кодер – устройство, преобразующее квантованные уровни в последовательность ИКМ bk(n); Модулятор – устройство, формирующее сигнал, амплитуда, фаза или частота которого меняется в соответствии с сигналом bk(n); Выходное устройство ПДУ – осуществляет фильтрацию и усиление модулированного сигнала для предотвращения внеполосных излучений, и обеспечения требуемого соотношения сигнал/шум на входе приёмника; Линия связи – среда или технические сооружения, по которым сигнал поступает от передатчика к приёмнику. В линии связи на сигнал налагается помеха; Входное устройство ПРУ – осуществляет фильтрацию принятой смеси сигнал + шум; Детектор – преобразует принятый сигнал в ИКМ bk(n); ЦАП – цифро-аналоговый преобразователь, включающий: 1) Декодер – преобразует кодовые комбинации в импульсы; 2) Интерполятор и ФНЧ – устройства, восстанавливающие непрерывный сигнал из импульсов – отсчётов; Получатель – объект или система, которому передаётся информация. Временные диаграммы. 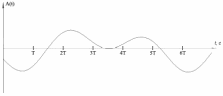 Рисунок 2 – Исходное сообщение. 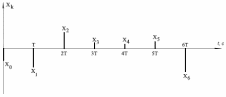 Рисунок 3 – Сигнал на выходе дискретизатора. 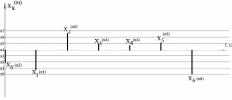 Рисунок 4 – Сигнал на выходе квантователя.  Рисунок 5 – Сигнал на выходе кодера. 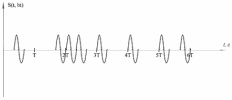 Рисунок 6 – Сигнал на выходе модулятора. 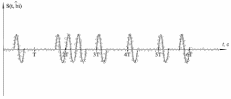 Рисунок 7 – Сигнал на выходе входного устройства (ПРУ) – вход детектора. 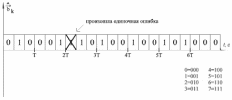 Рисунок 8 - Сигнал на выходе решающего устройства. 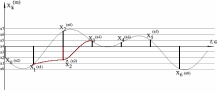 Рисунок 9 – Сигнал на выходе декодера. 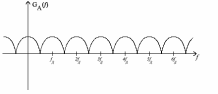 Рисунок 10 – Спектр сигнала на выходе дискретизатора. Пункт 1. По заданной функции корреляции исходного сообщения: а) рассчитать интервал корреляции, спектр плотности мощности и начальную энергетическую ширину спектра сообщения: Рассчитаем интервал корреляции: 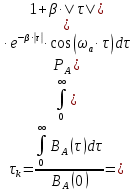 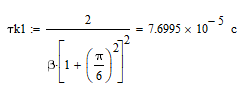 Рассчитаем энергетический спектр или спектр плотности мощности: 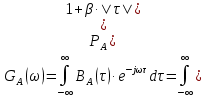 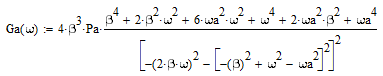 Рассчитаем начальную энергетическую ширину спектра сообщения: 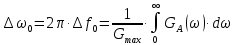 Для нахождения Gmax возьмём производную от GA(ω) её к нулю: 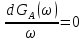 , ω = 0 , ω = 0Тогда получаем: Подставляя Gmax в выражение для ∆ω0 получаем: б) построить в масштабе графики функции корреляции и спектра плотности мощности; отметить на них найденные в п. а) параметры: 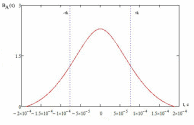 Рисунок 11 – График функции корреляции. 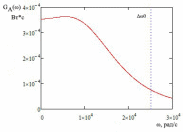 Рисунок 12 – График спектра мощности GA(ω). Пункт 2. Считая, что исходное сообщение воздействует на идеальный фильтр нижних частот (ИФНЧ) с единичным коэффициентом ширине спектра сообщения, рассчитать среднюю квадратичную погрешность фильтрации (СКПФ) сообщения, среднюю мощность отклика ИФНЧ, частоты и интервал временной дискретизации отклика ИФНЧ: Мощность отклика ИФНЧ равна: 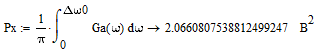 Средняя квадратичная погрешность фильтрации равна: Найдём частоту (fд) и интервал временной дискретизации (Тд): 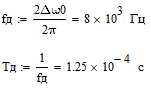 Пункт 3. Полагая, что последовательность дискретных отсчётов на выходе дискретизатора далее квантуется по уровню с равномерной шкалой квантования: а) рассчитать интервал квантования, пороги и уровни квантования, среднюю квадратическую погрешность квантования СКПК: Рассчитаем шаг квантования: Найдём пороги квантования: 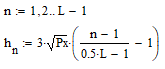 Таблица 2. Пороги квантования.
Найдём уровни квантования: 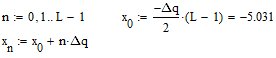 Таблица 3. Уровни квантования.
Найдём среднюю квадратическую погрешность квантования (мощность шума квантования): 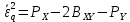 , где Px и PY соответственно мощности (дисперсии) входного и выходного сигналов квантователя, а BXY – коэффициент взаимной корреляции между этими сигналами. , где Px и PY соответственно мощности (дисперсии) входного и выходного сигналов квантователя, а BXY – коэффициент взаимной корреляции между этими сигналами.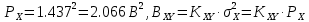 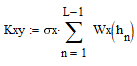 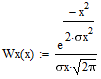 - ФПВ гауссовской случайной величины х. - ФПВ гауссовской случайной величины х.Таблица 4. Значения ФПВ гауссовской случайной величины.
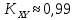 , следовательно , следовательно 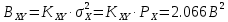 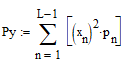 , где Pn – распределение вероятностей дискретной случайно величины y = xn, n = 0, L-1. , где Pn – распределение вероятностей дискретной случайно величины y = xn, n = 0, L-1. 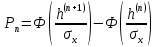 , n = 0, L-1, где , n = 0, L-1, где 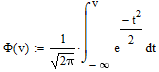 - табулированная функция Лапласа. - табулированная функция Лапласа.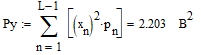 Получаем, что мощность шума квантования: 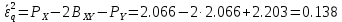 B2. B2.б) построить в масштабе характеристику квантования: 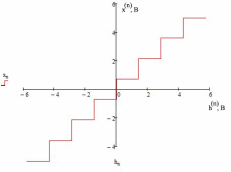 Рисунок 13 – Характеристика квантования (L=8). Пункт 4. Рассматривая отклик квантователя как случайный дискретный сигнал с независимыми значениями на входе L-ичного дискретного канала связи (ДКС): а) рассчитать закон и функцию распределения вероятностей квантованного сигнала, а также энтропию, производительность и избыточность L-ичного дискретного источника: 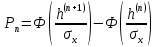 , n = 0, L-1, где , n = 0, L-1, где 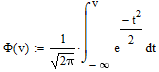 - табулированная функция Лапласа. - табулированная функция Лапласа.Таблица 5 – Таблица значений распределения вероятностей.
Интегральное распределение вероятностей: 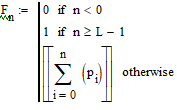 Рассчитаем энтропию 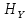 : : 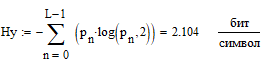 Производительность 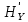 в ДКС определяется соотношением: в ДКС определяется соотношением: Избыточность последовательности источника: б) построить в масштабе графики рассчитанных закона и функции распределения вероятностей: 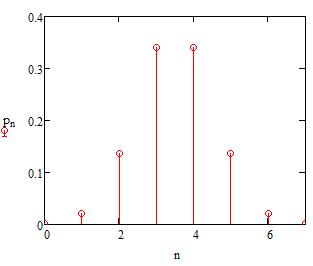 Рисунок 14 – График закона распределения вероятности. 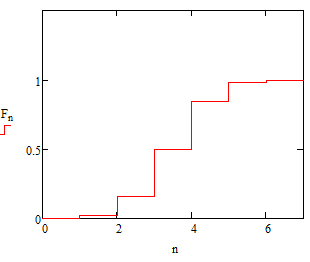 Рисунок 15 – График функции распределения вероятности. Пункт 5. Закодировать значения L-ичного дискретного сигнала двоичным блочным примитивным кодом, выписать все кодовые комбинации кода и построить таблицу кодовых расстояний кода.  При организации цифровой связи широкое распространение получило двоичное кодирование, когда кодовые символы принимают только два значения b0 = 0 и b1 = 1. Процедура кодирования состоит в следующем: физические уровни x(n), n = 0, L-1, вначале пронумеровываются, т.е. заменяются их номерами x(n) n, а затем эти десятичные числа представляют в двоично системе счисления с основанием 2. Это представление имеет вид: 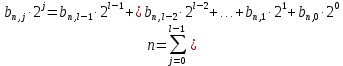 , где , где 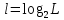 , , 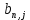 – двоичный кодовый символ (0 или 1) десятичного числа n, расположенный в j-ой позиции кодовой комбинации – двоичный кодовый символ (0 или 1) десятичного числа n, расположенный в j-ой позиции кодовой комбинации 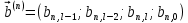 . .L = 8, соответственно, 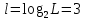 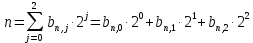 Тогда получим следующие кодовые комбинации: 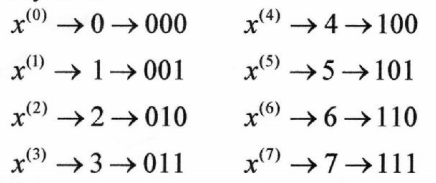 Образуется сигнал импульсно-кодовой модуляции (ИКМ). Кодовым расстоянием dmn между двумя двоичными кодовыми комбинациями 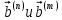 называют количество позиций в которых одна кодовая комбинация отличается от другой. называют количество позиций в которых одна кодовая комбинация отличается от другой. Таблица 6 - Таблица кодовых расстояний.
а) рассчитать априорные вероятности передачи по двоичному ДКС символов нуля и единицы, начальную ширину спектра сигнала ИКМ: Т.к. среднее число нулей 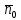 и среднее число единиц и среднее число единиц 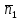 в сигнале ИКВ одинаково, то и вероятности их появления одинаковы: p(0) = p(1) = 0.5. в сигнале ИКВ одинаково, то и вероятности их появления одинаковы: p(0) = p(1) = 0.5.Ширина спектра сигнала ИКМ равна: 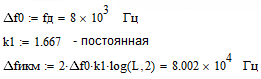 Пункт 6. Полагая, что для передачи ИКМ сигнала по непрерывному каналу связи (НКС) используется гармонический переносчик: а) рассчитать нормированный к амплитуде переносчика спектр модулированного сигнала и его начальную ширину спектра: Сигнал ДАМ представляется в виде:  Разложение сигнала по гармоническим составляющим имеет следующий вид: 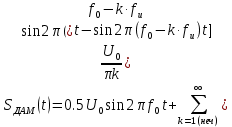 Спектр сигнала имеет только нечётные гармонические составляющие на частотах 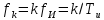 , k = 1, 3, 5… , k = 1, 3, 5…При неизвестной амплитуде U0 вычисляют нормированный спектр 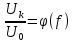  Ширина спектра сигнала ДАМ: 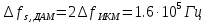 . .Таблица 7 – Значения спектра модулированного сигнала.
б) построить в масштабе график нормированного спектра сигнала дискретной модуляции и отметить на нём найденную ширину спектра: 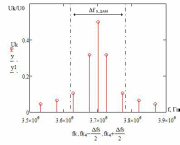 Рисунок 16 – График нормированного спектра сигнала дискретной модуляции. Пункт 7. Рассматривая НКС как аддитивный гауссовский канал с ограниченной полосой частот, равной ширине спектра сигнала дискретной модуляции, и заданными спектральной плотностью мощности помехи и отношением сигнал-шум: а) рассчитать приходящиеся в среднем на один двоичный символ мощность и амплитуду модулированного сигнала, дисперсию (мощность) аддитивной помехи в полосе частот сигнала, пропускную способность НКС: Мощность гауссовского белого шума 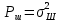 в полосе пропускания ПФ геометрически определяется как площадь прямоугольника с высотой G0 и основанием в полосе пропускания ПФ геометрически определяется как площадь прямоугольника с высотой G0 и основанием 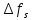 : :Учитывая, что начальное соотношение сигнал-шум (ОСШ) 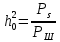 на входе детектор приёмника известно, находим мощность сигнала дискретной модуляции, обеспечивающей это ОСШ: на входе детектор приёмника известно, находим мощность сигнала дискретной модуляции, обеспечивающей это ОСШ:Рассчитаем приходящиеся в среднем на один двоичный символ мощность и амплитуду модулированного сигнала: Пропускная способность НКС характеризует максимально возможную скорость передачи информации по данному каналу. Она определяется: б) построить в масштабе четыре графика функций плотности вероятностей (ФПВ) мгновенных значений и огибающих узкополосной гауссовской помехи (УГП) и суммы гармонического сигнала с УГП. ФПВ мгновенных значений УГП имеют вид гауссовского распределения с числовыми характеристиками 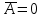 – математическое ожидание, – математическое ожидание, 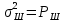 – мощность. – мощность.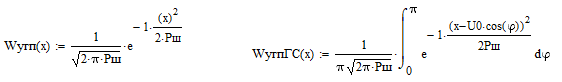 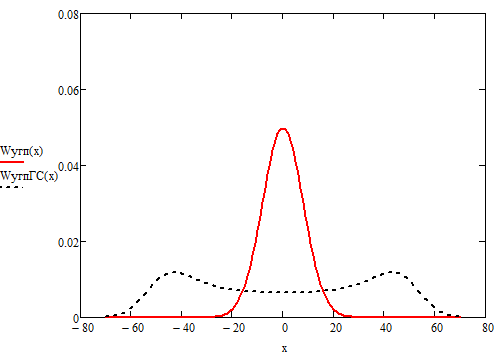 Рисунок 17 – Графики функций плотности вероятностей. Огибающая гаусссовской помехи распределена по закону Рэлея, а огибающая принимаемой суммы гармонического сигнала + УГП подчиняется обобщённому распределению Рэлея: 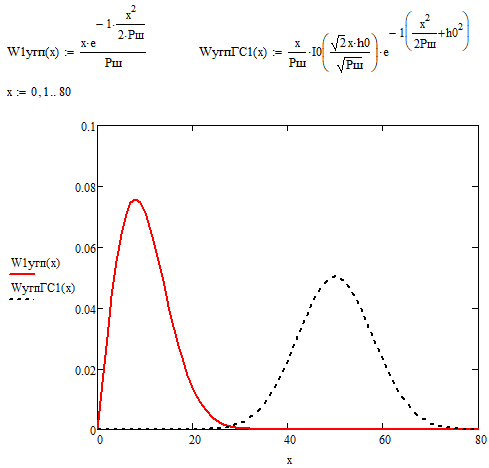 Рисунок 18 – Огибающие узкополосной гауссовской помехи и принимаемой суммы гармонического сигнала + УГП. Пункт 8. С учётом заданного вида приёма (детектирования) сигнала дискретной модуляции: а) рассчитать среднюю вероятность ошибки в двоичном ДКС, скорость передачи информации по двоичному симметричному ДКС, показатель эффективности передачи сигнала дискретной модуляции по НКС: За количественную меру помехоустойчивости в системах электросвязи принимают среднюю на бит вероятность ошибки: 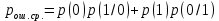 . При равенствах априорных вероятностей p(0) = p(1) = 0.5, а также условных вероятностей p(1/0) = p(0/1) = pош (условие симметричности двоичного ДКС), средняя на бит вероятность ошибки равна . При равенствах априорных вероятностей p(0) = p(1) = 0.5, а также условных вероятностей p(1/0) = p(0/1) = pош (условие симметричности двоичного ДКС), средняя на бит вероятность ошибки равна 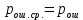 . .Скорость передачи информации по двоичному симметричному ДКС, когда p(1/0) = p(0/1) = pош, определяется:  Так как вероятность ошибок pош для различных видов сигналов зависят от h2 на входе детектора, то и R2 зависит от ОСШ. Для сравнения скорости R2 = Ψ(h2) при данном виде модуляции и способе приёма с пропускной способностью НКС С = Ψ1(h2) вводят показатель эффективности: 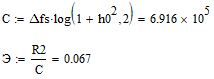 б) изобразить схему приёмника сигналов дискретной модуляции и коротко описать принцип его работы, пояснить случаи, когда он выносит ошибочные решения 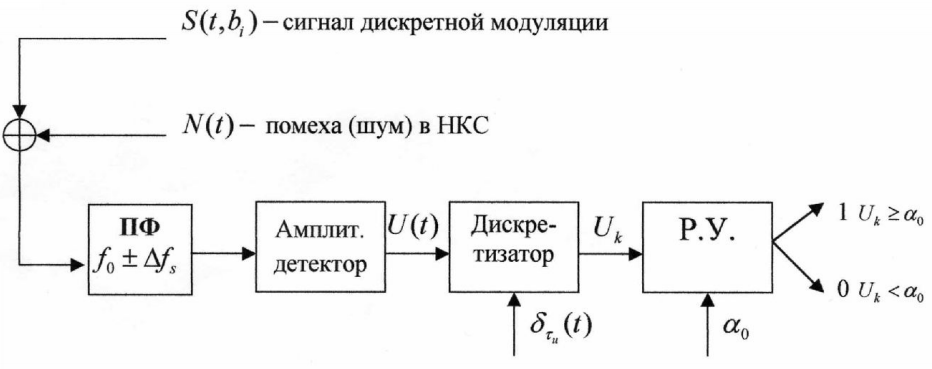 Рисунок 19 – Приёмник сигналов ДАМ. Амплитудный детектор, представляющий собой нелинейный преобразователь и ФНЧ, выделяет огибающую принимаемого сигнала ДАМ, прошедшего полосовой фильтр с эффективной полосой пропускания равной 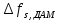 . К дискретизатору проводятся отклик детектора U(t) и последовательность дискретизирующих импульсов . К дискретизатору проводятся отклик детектора U(t) и последовательность дискретизирующих импульсов 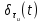 с периодом τи, которые необходимы для взятия отсчета в середине посылки длительностью τи. В РУ (решающем устройстве) отсчёты Uk сравниваются с пороговым напряжением α0 и принимается решение – передана 1, если Uk ≥ α0, или передан 0, если Uk < α0. Под действием помех в канале связи амплитуда сигнала изменяется и РУ может ошибаться: при передаче 0 принимать 1 или же при передаче 1 принимать 0. с периодом τи, которые необходимы для взятия отсчета в середине посылки длительностью τи. В РУ (решающем устройстве) отсчёты Uk сравниваются с пороговым напряжением α0 и принимается решение – передана 1, если Uk ≥ α0, или передан 0, если Uk < α0. Под действием помех в канале связи амплитуда сигнала изменяется и РУ может ошибаться: при передаче 0 принимать 1 или же при передаче 1 принимать 0. Пункт 9. Рассматривая отклик детектора ПРУ как случайный дискретный сигнал на выходе L-ичного ДКС: а) рассчитать распределение вероятностей дискретного сигнала на выходе детектора, скорость передачи информации по L-ичному ДКС, относительные потери в скорости передачи информации по L-ичному ДКС: Распределение вероятностей дискретного сигнала на выходе детектора определяется выражением: 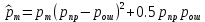 , m=n=0,7, где , m=n=0,7, где 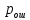 – вероятность ошибки в двоичном симметричном ДКС; – вероятность ошибки в двоичном симметричном ДКС; 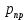 – вероятность правильного приёма двоичного символа, – вероятность правильного приёма двоичного символа, 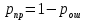 . .Таблица 8 – Вероятности дискретного сигнала на выходе детектора.
Для определения скорости передачи информации RL по L-ичному ДКС воспользуемся соотношением: 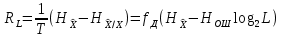 , где , где Рассчитаем энтропию восстановленного L-ичного сообщения: 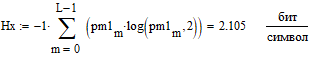 Тогда RL: Зная производительность 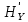 L-ичного источника (скорость ввода информации в ДКС) и скорость передаваемого по ДКС информации RL находим величину относительных потерь в скорости: L-ичного источника (скорость ввода информации в ДКС) и скорость передаваемого по ДКС информации RL находим величину относительных потерь в скорости: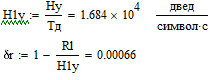 б) построить в масштабе график закона распределения вероятностей отклика декодера и сравнить его с законом распределения вероятностей отклика квантователя. 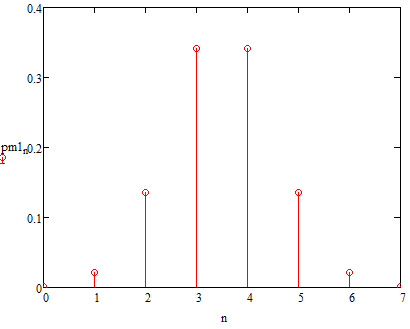 Рисунок 20 – Закон распределения вероятностей отклика декодера. Пункт 10. Полагая ФНЧ на выходе ЦАП приёмника идеальным с полосой пропускания, равной начальной энергетической ширине спектра исходного сообщения: а) рассчитать дисперсию случайных импульсов шума передачи на выходе интерполятора ЦАП, среднюю квадратическую погрешность шума передачи (СКПП), суммарную начальную СКП восстановления непрерывного сообщения (ССКП), относительную СКП (ОСКП): Дисперсия случайных импульсов шума передачи на выходе интерполятора ЦАП определяется: 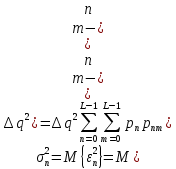 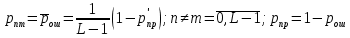 , где , где 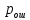 – вероятность ошибки в двоичном симметричном ДКС. – вероятность ошибки в двоичном симметричном ДКС.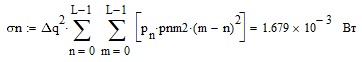 Рассчитаем СКПП: 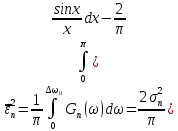 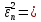 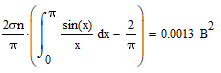 В виду того, что погрешность фильтрации 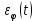 , шум квантования , шум квантования 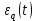 шум передачи шум передачи 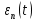 – независимые случайные процессы, то суммарная СКП восстановления непрерывного сообщения – независимые случайные процессы, то суммарная СКП восстановления непрерывного сообщения 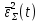 будет равна сумме СКП указанных процессов: будет равна сумме СКП указанных процессов: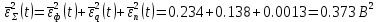 Тогда относительная суммарная СКП восстановленного сообщения будет равна: 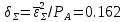 Пункт 11. В виду того, что выбор начальной энергетической ширины спектра исходного сообщения не приводит к минимуму ОСКП, решить оптимизационную задачу: с помощью ЭВМ определить оптимальную энергетическую ширину спектра сообщения, доставляющую минимум относительной суммарной СКП его восстановления. Относительная суммарная СКП восстановления сообщения равна:  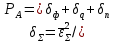 Не трудно показать, что относительные СКП фильтрации 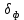 , квантования , квантования 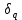 и передачи и передачи 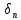 зависят от энергетической ширины спектра сообщения зависят от энергетической ширины спектра сообщения 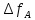 различным образом: различным образом: 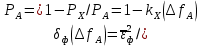 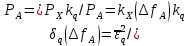 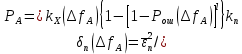 где kn = 9.07, kq = 0.081, т.к. 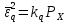 , а , а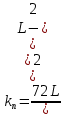 , где , где 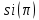 – интегральный синус: – интегральный синус: 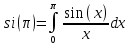 ; Fn – интегральный закон распределения. ; Fn – интегральный закон распределения. 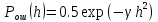 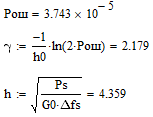 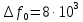 Гц; Гц; 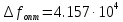 Гц. Гц. 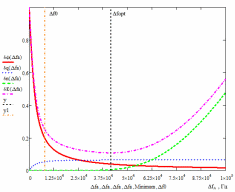 Рисунок 21 – Графики относительных СКП фильтрации, квантования и передачи. Вывод: суммарная величина относительной СКП имеет минимум при оптимально выбранной энергетической ширине спектра исходного сообщения. В смешанной системе связи сообщения передаются с искажениями, которые возникают при фильтрации, квантовании двоичном и L-ичном ДКС. Чтобы уменьшить ОСКП, необходимо увеличить число уровней квантования, из-за чего уровень шума квантования должен уменьшиться, а спектр сигнала в канале – увеличиться (расшириться). Шум квантования уменьшить можно неравномерным квантователем. Приложение. Список литературы. Санников В.Г., Курсовая работа и методические указания по ее выполнению, Учебное пособие/МТУСИ, 1994. – 40с. Курс лекций Поборчая Н.Е., МТУСИ, 2020. Зюко А.Г., Клоковский Д.Д., ТЭС: Учебник для вузов, Радио и связь, 1998. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

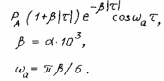
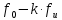 , Гц
, Гц